An introduction to direct methods

The most important phase relationships and their application in solving the phase problem

H. Schenk

Introduction

The term 'direct methods' is applied to that class of methods which seek directly to solve the phase problem by the use of phase relationships based on the observed intensities.

The object of this pamphlet is to familiarize the reader with the phase relationships used in Direct Methods, and to explain why they work and how they are used in practice. Some prior knowledge of the phase problem, the structure-factor equation and the application of Fourier theory in crystal-structure analysis is assumed.

Notation

H = Laue indices h k l of a reflection

K = Laue indices h₁ k₁ l₁ of another reflection

$\theta_H$ = Bragg angle of a reflection H

I_H = intensity of a reflection H ( $I_H\propto\vert F_H\vert^2$ )

F_H = the structure factor of H. In this work F_H will be corrected for thermal motion and brought onto an absolute scale.

E_H = normalised structure factor of H

U_H = unitary structure factor of H

G_H = structure factor of H based on the squared structure

$\phi_H$ = phase of reflection H

N = number of atoms in the unit cell

f_j = scattering factor of atom j

Z_j = atomic number of atom j

r_j = position of atom j in vector notation

x_j, y_j, z_j = position of atom j in Cartesian coordinates

E₃ = N^-1/2|E_HE_KE_-H-K|

E₄ = N^-1|E_HE_KE_LE_-H-K-L|

Strong and weak structure factor magnitudes F_H

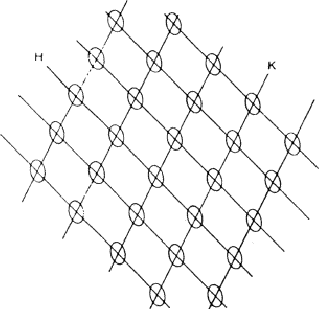
If, in a crystal structure, atoms lie in the neighbourhood of a set of planes H, as indicated in Fig. 1a, then reflection by planes H is strong and hence the intensity I_H is large. Of course, the converse is also true: if one observes a large intensity I_H, then the atoms lie near planes as indicated in Fig. 1a. This statement follows also from the structure-factor expression:

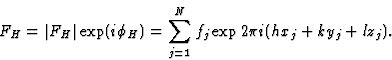
$\begin{displaymath} F_H = \vert F_H\vert\exp (i{\phi}_H) = \sum^N_{j=1} f_j \exp 2{\pi}i(hx_j + ky_j + lz_j).\end{displaymath}$

A large F_H will be found if (hx_j + ky_j + lz_j) mod 1 is approximately constant for all j; or, in other words, if all atoms lie near one of the planes H. The phase $\phi_H$ depends on the value of the constant and changes with the origin.

**Figure 1:** A reflected beam H is strong when the atoms lie in the neighbourhood of the set of planes H (a) and low when the atoms are spread out with respect to the planes H (b).
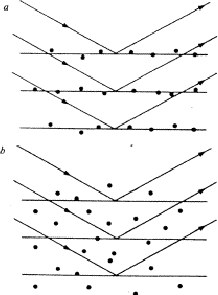$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

Conversely, a structure-factor magnitude |F_H| is small, if the atoms are randomly distributed with respect to the planes H, as shown in Fig. 1b.

The electron density can be thought of as a superposition of density waves parallel to lattice planes, the amplitudes of which are the |F_H|-values, the relative phases being given by the $\phi_H$ -values. We will see later that these density waves afford a physical picture of the phase relationships used in Direct Methods.

Normalized structure factors E_H

Note: in this text F_H designates the structure factor corrected for thermal motion and brought to an absolute scale; generally this is done using a Wilson plot. Since the scattering factor of any atom decreases for larger reflection angle $\theta$ , and the expected intensity $\langle \vert F\vert^2\rangle_{\theta}$ of a reflection is given by

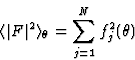$\begin{displaymath} \langle\vert F\vert^2\rangle_{\theta} = \sum^N_{j=1} f^2_j(\theta)\end{displaymath}$

(1)

reflections measured at different $\theta$ -values can not be compared directly. Expression (1) can be used to calculate the so called normalized structure factor

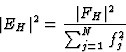$\begin{displaymath} \vert E_H\vert^2 = \frac{\vert F_H\vert^2}{\sum^N_{j=1}f^2_j}\end{displaymath}$

(2)

It is obvious from a comparison of (1) and (2) that $\langle$ E²_H $\rangle$ = 1 for all values of $\theta$ .

The structure-factor expression in terms of the normalized structure factor is then:

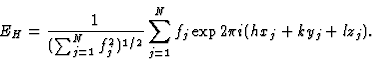$\begin{displaymath} E_H = \frac{1}{(\sum^N_{j=1} f^2_j)^{1/2}} \sum^N_{j=1} f_j \exp 2 {\pi}i(hx_j + ky_j + lz_j).\end{displaymath}$

(3)

If the form factor f_j has the same shape for all atoms (f_j = Z_jf), expression (3) can be written as

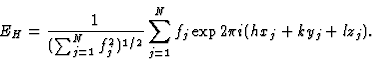$\begin{displaymath} E_H = \frac{1}{(\sum^N_{j=1} f^2_j)^{1/2}} \sum^N_{j=1} f_j \exp 2 {\pi}i(hx_j + ky_j + lz_j).\end{displaymath}$

(4)

This is clearly the structure factor formula of a point atom structure, because no $\theta$ -dependent factors are present any more.

In order to find the maximum value of |E|, let us consider an equal atom structure for which the structure factor (4) further reduces to

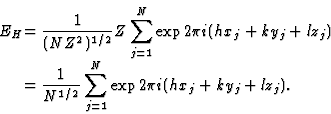$\begin{displaymath} \begin{array} {@{}r@{}l} E_H&\displaystyle= \frac{1}{(NZ^2)^... ...}i(hx_j + ky_j + lz_j).\hbox{\rule{0cm}{12pt}\hfill}\end{array}\end{displaymath}$

(5)

The maximum possible value of |E_H| is N/N^1/2 = N^1/2.

The unitary structure factor U was used extensively in the early literature on Direct Methods:

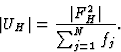$\begin{displaymath} \vert U_H\vert=\frac{\vert F^2_H\vert}{\sum^N_{j=1}f_j}.\end{displaymath}$

(6)

The denominator represents the maximum possible value of F_H and thus U_H varies between 0 and 1. In the equal atom case the relation between U_H and |E_H| is given by

|E_H|² = N|U_H|².

(7)

which can easily be verified by the reader from (6) and (2).

The |E|'s of H and 2H: the 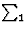$\sum_1$ relationship

The $\sum_1$ relation is the first phase relationship which will be considered here; it estimates in centrosymmetric space groups the phase of reflection 2H on the basis of the magnitudes |E_H| and |E_2H|. To start with, geometrical considerations will be applied to reflections with simple indices.

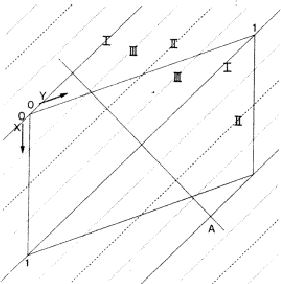
In a centrosymmetric crystal only phases of 0 and $\pi$ occur; provided that the phase of the 110 reflection is 0 the maxima of the associated electron density wave are found at the lines I of Fig. 2 and the minima at the lines II. If the phase of 110 is $\pi$ , the maxima and minima are interchanged. The lines where the electron density wave has 0 value are marked with III. Thus in the event |E₁₁₀| is large and $\phi_{110}$ = 0, the electron density is mainly concentrated in the shaded areas of Fig. 3. For the electron density wave associated with the 220 reflection the maxima are found at both lines I and II in Fig. 2 in the case its phase is 0 and the minima at the lines III. Thus, when |E₂₂₀| is large and $\phi_{220}$ = 0 the atoms must lie in shaded areas in Fig. 4. A similar drawing can be made for $\phi_{220}$ = $\pi$ .

**Figure 2:** Lines of equal contribution to the electron density of the reflections hh0. E.g. for reflections 110 with $\phi_{110}$ = 0 the contribution to the electron density is maximum at lines I, minimum at lines II and zero at lines III.
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

**Figure 3:** In case |*E₁₁₀*| is large and $\phi_{110}$ = 0 the atoms are likely to be found in the shaded areas.
$\begin{figure} \includegraphics {fig3.ps} \end{figure}$

**Figure 4:** For |*E₂₂₀*| large and $\phi_{220}$ = 0 the electron density is more likely to be present in the vertically shaded areas.
$\begin{figure} \includegraphics {fig4.ps} \end{figure}$

The combination of the two electron density waves associated with the reflections 110 and 220 leads to Fig. 5, in which in the areas I maxima are found of both density waves. In the areas II the maximum of 220 coincides with the minimum of 110, resulting in a low density. In the event that both reflections have a large |E| value it is likely that the atoms are concentrated in the double shaded area.

In case the phase $\phi_{220}$ = $\pi$ , the vertically shaded areas shift to the blank regions of Fig. 5 and then there is no overlap between the horizontally (110) and vertically (220) shaded areas; this implies that no position for the atoms can be found in which they contribute strongly to both structure factors. As a result for $\phi_{220}$ = $\pi$ and $\phi_{110}$ = 0 it is not likely that both structure factor magnitudes |E₁₁₀| and |E₂₂₀| are large.

**Figure 5:** Superposition of Figs. 3 and 4. In the areas I the shaded areas from the 110 and 220 reflections coincide. In case both reflections are large this is a rather likely situation.
$\begin{figure} \includegraphics {fig5.ps} \end{figure}$

In conclusion, for large structure factors |E₁₁₀| and |E₂₂₀|, it is likely that $\phi_{220}$ = 0; this relationship is known as the $\sum_1$ relation.

Up to now no attention is paid to the situation $\phi_{110}$ = $\pi$ , the reader is invited to show that this gives no change in the formulation of the $\sum_1$ relation.

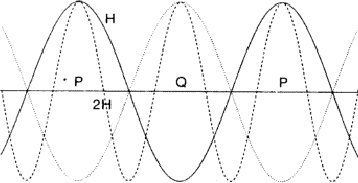
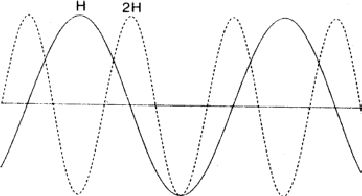
The comparison of H and 2H can be considered as a one-dimensional problem which can be understood by looking along line A in Fig. 2. In Fig. 6 the situation along this line is sketched with $\phi_H$ = $\phi_{2H}$ = 0 while in Fig. 7 $\phi_H$ = 0 and $\phi_{2H}$ = $\pi$ . Areas labelled P in Fig. 6 denote regions of considerable positive overlap, whereas in Fig. 7 only regions of minor positive overlap are seen. The implication is that for large |E_H| and |E_2H| the situation depicted in Fig. 6 is more probably true and thus $\phi_{2H}$ = 0. When $\phi_H$ = $\pi$ , as denoted by the dotted line in Fig. 6 the overlap areas marked Q show that $\phi_{2H}$ is still zero.

**Figure 6:** The drawn line H gives the electron density wave for $\phi_H$ = 0, and its dotted mirror image the wave for $\phi_H$ = $\pi$ . The maximum of the dashed line 2H coincides with the maxima of the drawn line H in P and with the maxima of the dotted one in Q. Thus if |E_H| and |E_2H| are large, it is likely that $\phi_{2H}$ = 0 whatever the phase of H.
$\begin{figure} \includegraphics {fig6.ps} \end{figure}$

**Figure 7:** Here the unlikely situation is depicted that for strong reflections H and 2H $\phi_H$ = 0 and $\phi_{2H}$ = $\pi$ . There is no positive overlap and therefore if |E_H| and |E_2H| are both large this situation is much more unlikely to exist than the situation of Fig. 7.
$\begin{figure} \includegraphics {fig7.ps} \end{figure}$

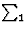The $\sum_1$ -relation from a Harker-Kasper inequality

In 1948 Harker and Kasper published their paper on inequality relationships, which actually opened the field of direct methods. They applied the Cauchy inequality:

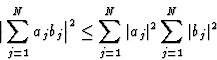$\begin{displaymath} \big\vert\sum^N_{j=1} a_jb_j\big\vert^2 \leq \sum^N_{j=1}\vert a_j\vert^2 \sum^N_{j=1}\vert b_j\vert^2\end{displaymath}$

(8)

to the structure factor equation. For instance the partitioning of the unitary structure-factor equation in $P\overline{1}$ into:

$\begin{displaymath} U_H = \sum_{j=1} n_j \cos 2 {\pi} H{\cdot}r = \sum_{j=1} a_jb_j\end{displaymath}$

(9)

such that a_j = n1/2_j and $b_j = n^{1/2}_j \cos 2 {\pi}H{\cdot}r$ leads to

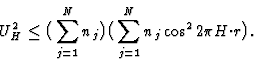$\begin{displaymath} U^2_H \leq \big(\sum^N_{j=1} n_j\big)\big(\sum^N_{j=1} n_j \cos^2 2{\pi}H{\cdot}r\big).\end{displaymath}$

(10)

From the definition of the unitary structure factor it follows that

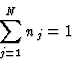$\begin{displaymath} \sum^N_{j=1} n_j = 1\end{displaymath}$

(11)

and the second factor can be reduced as follows

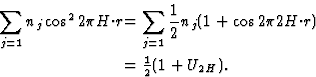$\begin{displaymath} \begin{array} {@{}r@{}l} \displaystyle \sum_{j=1} n_j \cos^2... ...\frac{1}{2}(1+U_{2H}). \hbox{\rule{0cm}{12pt}\hfill}\end{array}\end{displaymath}$

(12)

These results used in (10) give

$\begin{displaymath} U^2_H \leq \frac{1}{2}(1 + U_{2H}).\end{displaymath}$

(13)

In case $U^2_H \gt \frac{1}{2}$ then $U_{2H}\geq 0$ or in other words the sign of reflection 2H is positive whatsoever its |U_2H| value is. Note that the sign of H may have both values. In practice $U^2_H \gt \frac{1}{2}$ does not often occur. However, when |U_2H| is large, expression (13) requires the sign of 2H to be positive even if U_H is somewhat smaller than $\frac{1}{2}$ . Moreover, when |U_H| and |U_2H| are reasonably large, but at the same time (13) is fulfilled for both signs of 2H, it is still more likely that S_2H = + than that S_2H = -. For example, for |U_H| = 0.4 and |U_2H| = 0.3, S_2H = + leads in (13) to 0.16 $\leq$ 0.5 + 0.3 which is certainly true, and S_2H = - to $0.16 \leq 0.5 - 0.3$ which is also true. Then probability arguments indicate that still S_2H = + is the more likely sign. The probability is a function of the magnitudes |U_H| and |U_2H| and in this example the probability of S_2H = + being correct is $\gt 90\%$ .In conclusion the mathematical treatment leads to the same result as the graphic explanation from the preceding paragraph: the $\sum_1$ relationship.

Large |E_H|, |E_K| and |E_-H-K|: the triplet relationship

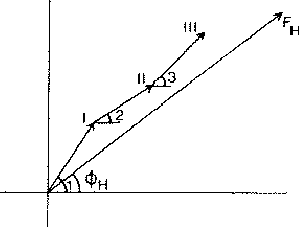
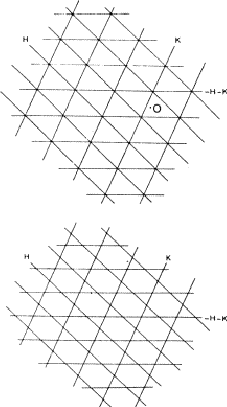
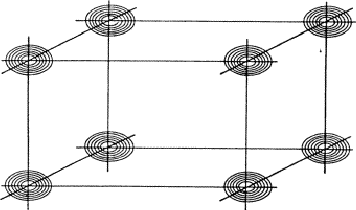
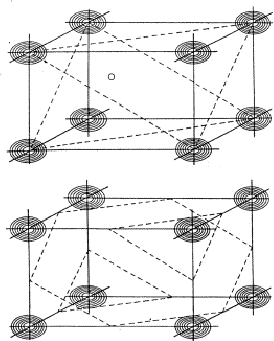
If two reflections H and K are both strong then the electron density is likely to be found in the neighbourhood of the two sets of equidistant planes defined by H and K. That is to say the electron density will be found near the lines of intersection of the planes H and K as indicated in projection in Fig. 9. A large |E| for reflection -H-K as well implies that the electron density will also peak in planes lying d_-H-K apart. It is therefore most likely that these planes run through the lines of intersection of the planes H and K, in other words that the three sets of planes have their lines of intersection in common (see Fig. 10a). Then by choosing an origin at an arbitrary point the triplet phase relationship can be found from a planimetric theorem, proved in Fig. 11:

AO/AD + BO/BE + CO/CF = 2

(14)

which is equivalent to

$\begin{displaymath} \phi_{-H-K} + \phi_H + \phi_K + 2 {\cdot} 2 {\pi} = 0\quad(\mbox{modulo } 2 {\pi}).\end{displaymath}$

(15)

Because the choice of the origin is arbitrary it is obvious that expression (15) is independent of the position of the origin: relations of this type are usually called 'structure invariants', although a more logical name would be 'origin invariants'.

**Figure 8:** A few large terms (I: F_KF_H-K; II: F_K'F_H-K'; etc) from the right hand side of expression (27) in a phase diagram. It can be seen that their phases (1: $\phi_K + \phi_{H-K}$ ; 2: $\phi_{K'} + \phi_{H-K'}$ ; etc) are approximately equal to $\phi_H$ .
$\begin{figure} \includegraphics {fig8.ps} \end{figure}$

**Figure 9:** If the reflections H and K are both strong, then the electron density will likely lie in the neighbourhood of the intersecting lines of the two sets of equidistant planes defined by H and K.
$\begin{figure} \includegraphics {fig9.ps} \end{figure}$

**Figure 10:** When H and K are strong and -H-K is strong as well it is more likely that the planes of high density of -H-K run through the lines of intersection (a) than just in betwen (b).
$\begin{figure} \includegraphics {fig10.ps} \end{figure}$

**Figure 11:** In an arbitrary triangle *ABC* an origin O has been arbitrarily drawn. Theorem: AO/AD + BO/BE + CO/CF = 2. Proof: AO/AD = AP/AC; CO/CF = CR/AC; BO/BE = BQ/BC = AS/AC; because RP = SC, AP + CR +AS = 2AC.
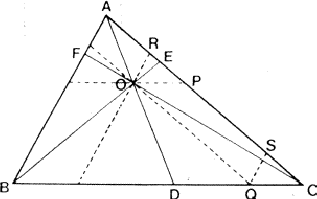$\begin{figure} \includegraphics {fig11.ps} \end{figure}$

In Fig. 10a the ideal situation is sketched and of course a small shift of the planes of largest density of -H-K does not affect the reasoning given above. However, the most unlikely position for these planes is the one indicated in Fig. 10b; here the planes -H-K of largest electron density keep clear of the lines of intersection of H and K. The triplet relationship therefore has a probability character and this is emphasised by formulating it as

$\begin{displaymath} \phi_H + \phi_K + \phi_{-H-K} \approx 0\end{displaymath}$

(16)

for large values of E₃ = N^-1/2|E_HE_KE_-H-K|. The $\approx$ -sign means that the most probable value of the triplet phase sum is 0. Clearly, the triplet product E₃ is large when all three reflections H, K and -H-K have large |E|-values.

The triplet relation from Sayre's equation

The earliest formulation of the triplet-relation (10) for the centrosymmetric case was via Sayre's equation (Sayre, 1952). This equation can be derived from Fourier theory as follows.

The electron density can be written as

$\begin{displaymath} {\rho}(r) = \frac {1}{V} \sum_H F_H \exp (-2{\pi}iH{\cdot}r)\end{displaymath}$

(17)

and upon squaring this function becomes

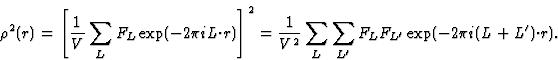$\begin{displaymath} \rho^2(r)=\left[\frac{1}{V} \sum_L F_L \exp (-2{\pi}iL{\cdot... ...ime}}F_LF_{L^{\prime}} \exp (-2{\pi}i(L + L^{\prime}){\cdot}r).\end{displaymath}$

(18)

(18) is rewritten by setting $H = L + L^{\prime}$ and $K = L^{\prime}$ to

$\begin{displaymath} \rho^2(r) = \frac{1}{V^2} \sum_H \sum_K F_K F_{H-K} \exp (-2{\pi}iH{\cdot}r).\end{displaymath}$

(19)

Because $\rho^2(r)$ is also a periodic function it can be written, by analogy with (17), as

$\begin{displaymath} \rho^2(r) = \frac{1}{V} \sum_H G_H \exp (-2{\pi}iH{\cdot}r)\end{displaymath}$

(20)

in which G_H is the structure factor of the squared structure. Comparing (19) and (20) it follows that

$\begin{displaymath} G_H = \frac{1}{V} \sum_K F_K F_{H-K}.\end{displaymath}$

(21)

The structure factor G_H is:

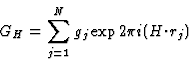$\begin{displaymath} G_H = \sum^N_{j=1} g_j \exp 2 {\pi}i(H{\cdot}r_j)\end{displaymath}$

(22)

in which g_j is the form factor of the squared atoms. For equal atoms (22) reduces to

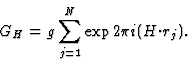$\begin{displaymath} G_H = g \sum^N_{j=1} \exp 2 {\pi}i(H{\cdot}r_j).\end{displaymath}$

(23)

The normal structure factor for equal atoms is

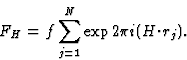$\begin{displaymath} F_H = f \sum^N_{j=1} \exp 2{\pi}i(H{\cdot}r_j).\end{displaymath}$

(24)

Thus from (23) and (24) we obtain

$\begin{displaymath} G_H = \frac{g}{f} F_H.\end{displaymath}$

(25)

Finally from (21) and (25) it follows that

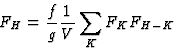$\begin{displaymath} F_H = \frac{f}{g} \frac{1}{V} \sum_K F_KF_{H-K}\end{displaymath}$

(26)

which is known as Sayre's Equation. It is emphasised that, given an equal-atom structure, Sayre's equation is exact. The summation (26) contains a large number of terms; however, in general it will be dominated by a smaller number of large |F_KF_H-K|. Rewriting (26) to

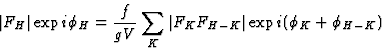$\begin{displaymath} \vert F_H\vert\exp i{\phi}_H = \frac{f}{gV} \sum_K \vert F_KF_{H-K}\vert \exp i({\phi}_K + {\phi}_{H-K})\end{displaymath}$

(27)

$\begin{displaymath} \exp i\phi_H \approx \exp i(\phi_K + \phi_{H-K})\end{displaymath}$

(28)

$\begin{displaymath} \phi_H \approx \phi_K + \phi_{H-K}\end{displaymath}$

$\begin{displaymath} \phi_{-H} + \phi_K + \phi_{H-K} \approx 0.\end{displaymath}$

(29)

Relation (29) is identical to (16), the triplet relation. Thus by introducing the obvious argument that the most important terms in Sayre's equation (27) must reflect the phase $\phi_H$ the triplet relation is found.

In the event that only a number of larger terms in (27) are available the scaling constant f/gV has no meaning. Nevertheless most likely the phase information included in these terms is correct and thus an expression such as

$\begin{displaymath} \exp i\phi_H = \frac{\sum_k \vert F_KF_{H-K}\vert\exp i(\phi... ...ert\sum_K\vert F_KF_{H-K}\vert\exp i(\phi_K + \phi_{H-K})\vert}\end{displaymath}$

(30)

in which K ranges over a limited number of terms may be very helpful.

The so called tangent formula (Karle and Hauptman, 1956)

$\begin{displaymath} \tan \phi_H = \frac{\sum_K E_3 \sin (\phi_K + \phi_{H-K})}{\sum_K E_3 \cos (\phi_K + \phi_{H-K})}\end{displaymath}$

(31)

in which the signs of numerator and denominator are used to determine the quadrant of the phase $\phi_H$ , is closely related to (30). This formula is used in almost all direct method procedures.

The positive quartet relation

The triplet relation, although a two-dimensional phase relation, is very successful in solving three-dimensional crystal structures. Nevertheless, it may be more appropriate to try to solve structures with three-dimensional phase relationships, the quartet relations.

The positive quartet relation is formulated as:

$\begin{displaymath} \phi_H + \phi_K + \phi_L + \phi_{-H-K-L} \approx 0\end{displaymath}$

(32)

for large E₄ = N^-1|E_HE_KE_LE_-H-K-L|.

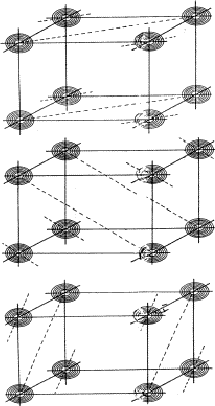
Analogous to the treatment of the triplet relation now three strong reflections H, K and L are combined and the electron density must be found in the sets of planes of Fig. 12. As a result the electron density will be found near the points of intersection of the three planes which are indicated for only a few planes from the sets in Fig. 13. For a strong reflection -H -K -L it is much more likely that its plane of maximum electron density will run through the points of intersection (Fig. 14a) than that it will clear these points (Fig. 14b). From Fig. 14a the quartet relation (32) follows as straightforward as the triplet relation from Fig. 10a (Schenk, 1981).

**Figure 12:** If the reflections H, K and L are strong, the electron density will probably lie in the neighbourhood of the three sets of equidistant planes defined by H, K and L.
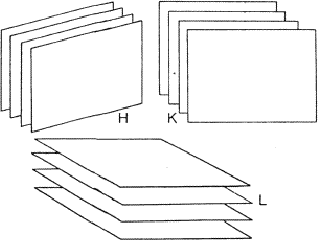$\begin{figure} \includegraphics {fig12.ps} \end{figure}$

**Figure 13:** The electron density will be found near the points of intersection of the three sets of planes H, K and L.
$\begin{figure} \includegraphics {fig13.ps} \end{figure}$

**Figure 14:** If reflection -H-K-L has also a large intensity, it is more likely that its planes of maximum intensity run through the points of intersection of H, K and L (a) than that they run clear of them (b).
$\begin{figure} \includegraphics {fig14.ps} \end{figure}$

This quartet relation, however, is not as strong as the triplet relation because of the factor N^-1 in E₄. It will be recalled that in E₃ a term N^-1/2 appears. The reliability is improved by combining the quartet with an identical one constructed from two triplets:

$\begin{displaymath} \phi_H + \phi_K + \phi_{-H-K} \approx 0\end{displaymath}$

$\begin{displaymath} +\frac{\phi_L + \phi_{-H-K-L} + \phi_{H+K} \approx 0}{\phi_H + \phi_K + \phi_L + \phi_{-H-K-L}} \approx 0\end{displaymath}$

(33)

which holds for large E₄ and large |E_H+K|. This can be understood by drawing the H+K reflection in Fig. 13, as indicated in Fig. 15a. Reflection H+K strong indicates that the electron density will be found near the intersection of H and K and thus a large |E_H+K| is an additional indication that quartet (32) is true. In Figs. 15b and 15c similar situations are sketched for the other two cross terms H + L and K + L, which both leads to sums of triplets analogous to (33) involving the phases $\phi_{H+L}$ and $\phi_{K+L}$ respectively. So in conclusion a large value of E₄ and large |E_H+K|, |E_H+L| and |E_K+L| are indications that the positive quartet relation (32) is likely to be true, and thus positive quartets are controlled by the magnitudes of 7 structure factors.

**Figure 15:** If H, K, L and -H-K-L are strong and the electron density will be found near their points of intersecting, the H + K reflection, indicated in (a) with a dotted line, is expected to be strong, conversely a large |E_H+K| supports the quartet relation (11). Figs (b) and (c) give the analogous situations with respect to the H + L and K + L reflections.
$\begin{figure} \includegraphics {fig15.ps} \end{figure}$

The negative quartet relation

In the event that the sum of the four phases is equal to $\pi$ :

$\begin{displaymath} \phi_H + \phi_K + \phi_L + \phi_{-H-K-L} = \pi\end{displaymath}$

(34)

the resulting relationship is referred to as the negative quartet relation and such a relationship exists for reasonably strong intensities for H, K, L and -H- K-L.

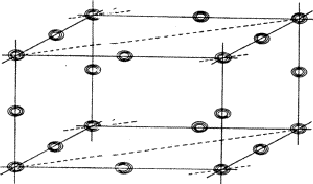
The planes of maximum for the 4 reflection involved in relation (34) are indicated in Fig. 16. It can be seen that for all indicated positions three out of four planes intersect. If atoms are located at these points the resulting unitary structure factors of H, K, L and -H-K-L will be 0.5, because three atoms lie in the planes and one lies halfway between. Thus for a negative quartet relation the reflections H, K, L and -H-K-L will in general not be found amongst the very strongest. The next question to be answered is: what is the intensity of reflection H + K, if the electron density is located near the marked points of Fig. 16? From Fig. 17 it can be easily seen that H + K will have a small |E|-magnitude: equal numbers of points of electron density concentration lie on the H + K planes and halfway in between. As the same holds for the other cross terms it can be stated that the negative quartet relation (34) is likely to be true for reasonably large values of E₄ and small |E_H+K|, |E_H+L| and |E_K+L|.

**Figure 16:** In the case of the negative quartet relation the planes of maximum electron density of H, K, L and -H-K-L run as indicated here. At distinct positions three planes intersect and there most likely the electron density will be found.
$\begin{figure} \includegraphics {fig16.ps} \end{figure}$

**Figure 17:** As Fig. 16 with the reflection H+K indicated by means of dotted lines. It is easily checked that this reflection is weak, because the electron density is distributed in equal amounts on and between the planes.
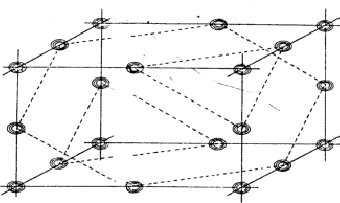$\begin{figure} \includegraphics {fig17.ps} \end{figure}$

How numerous are the reliable triplets and quartets?

In the following table numbers of relations are given together with their percentage of correct indications for triplets, quartets and negative quartets above variable thresholds of respectively the triplet product E₃ and a quartet product E^*₄ (Schenk, 1973). The numbers are given for an aza-steroid with N = 40, in space group $P\overline{1}$ .


		Triplets		Positive quartets		Negative quartets

E₃	no. relations	% correct relations	E₄	no.	%	no.	%

6.0	21	100	6.0	185	100
4.0	143	100	4.0	1213	100
3.0	353	100	3.0	3295	100	1	100
2.5	583	99.8	2.5	5813	99.8	2	100
2.0	980	99.7	2.0	10,006	99.5	17	100
1.5	1823	99.2	1.5	13,114	98.8	38	100
1.0	3395	96.9

As can be seen many relations are available to solve this small N = 40 structure. As a rule the number of useful triplets and quartets diminishes as N increases; this effect is quite noticeable for quartets.

One comment regarding the use of negative quartets. If phase relationships such as the triplet relation

$\begin{displaymath} \phi_H + \phi_K + \phi_{-H-K} \approx 0.\end{displaymath}$

are used exclusively and there is no translational symmetry, the trivial solution with all phases $\phi_H$ = 0 is the most consistent one. To find phases equal to $\pi$ (e.g. in space group $P\overline{1}$ ) it is necessary to use relations of the type

$\begin{displaymath} \phi_H + \phi_K + \cdots \approx \pi.\end{displaymath}$

Thus relations such as negative quartets (34), although few in number, play an important role in these structure determinations.

Direct methods in action

The first direct method, by means of which structures were solved, was the symbolic addition method. This method originates from Gillis (1948), however, due to the work of Karle and Karle (1966) it developed to a standard method. The problem can be defined as how do we find m phases, provided there are n phase relationships ( $n \gg m$ )? In the first place a few ( $\leq$ 3) phases can be chosen to fix the origin and then, using phase relationships, new phases can be derived from these three. In general it will not be possible to phase all reflections in this way and hence a suitable reflection (large |E|, many relationships with large E₃) is given a symbolic phase and again the relationships are used to find new phases in terms of the already known ones. Usually it will be necessary to choose several symbols in order to phase most of the strong reflections. Finally the numerical values of the symbols are determined (e.g. by using negative quartet relations) and from the known phases a Fourier map can be calculated. This process is known as the symbolic addition method. Most structures are now solved by multi-solution tangent refinement procedures, which use many starting sets of numerical phases and the tangent formula (31) to extend and refine the phases. The correct solution may then be selected by using figures of merit, based e.g. on the internal consistency of the triplet-relations, or on the negative quartets.

Additional literature

In the preceding chapters the main object was to clarify the basis of the present direct methods. In this chapter a brief guide to additional literature is given.

This triplet relation originates from the early fifties and was implicitly present in the important papers by Harker and Kasper (1948), Karle and Hauptman (1950) and Sayre (1952). For the cenytrosymmetric case it was explicitly formulated by Sayre (1952), Cochran (1952), Zachariasen (1952) and Hauptman and Karle (1953). The latter authors gave it its probability basis, which was independently derived by Kitaigorodsky (1954) as well. The noncentrosymmetric case was formulated first by Cochran (1955). Another useful expression related to the $\sum_2$ relation is the tangent formula (31) derived by Karle and Hauptman (1956).

A very important development was the use of symbols for tackling the set of triplet relations (1) in order to find the phases. Symbols are assigned to unknown phases such that a successful phase extension can be carried out. Later in the process in most cases the numerical values of the symbols can be determined. The use of symbols was first introduced by Gillis (1948) and later successfully applied by Zachariasen (1952) and Rumanova (1954), but due to the work of Karle and Karle (1963, 1966) the method could develop to a standard technique in crystallography. In particular the first structure determination of a non-centrosymmetric structure (Karle and Karle, 1964) proved the value of direct methods. The method has recently been described in detail by J. Karle (1974) and Schenk (1980a). The latter gives also some exercises. For centrosymmetric structures the symbolic addition procedure has been automized amongst others by Beurskens (1965), Germain and Woolfson (1968), Schenk (1969), Ahmed (1970), Dewar (1970), and Stewart (1970).

In noncentrosymmetric structures the programming problems are much greater and therefore the number of successful automatic program systems is smaller, examples are the systems of Dewar (1970) and the interactive system SIMPEL (Overbeek and Schenk, 1978).

Nowadays most of the structures are solved by multisolution tangent refinement procedures, which use many sets of numerical phases to start with and the tangent refinement (31) to extend and refine the phases. The most widely used procedure of this sort is the computer package MULTAN (Germain and Woolfson, 1968; Main, 1978; Main, 1980).

The positive seven-magnitude quartet relation (32) was first formulated by Schenk (1973) and at the same time a two-dimensional analogue of the negative quartet relationship proved to be useful (Schenk and de Jong, 1973; Schenk, 1973b). The negative quartet in theory and practice was then published by Hauptman (1974) and Schenk (1974). In the latter paper the first Figure of Merit based on negative quartets was successfully formulated and tested. Theories concerning 7 magnitude-quartets were developed later, among which the one of Hauptman (1975) is best established. Applications of quartets include their use in starting set procedures and figures of merit, further brief details of which can be found in a recent review article (Schenk, 1980b).

References

Ahmed, F. R., in F. R. Ahmed (ed.), Crystallographic Computing, pp. 55- 57, Copenhagen, Munksgaard (1970).

Beurskens, P. T., Thesis, Utrecht (1965).

Cochran, W., Acta Cryst. 5 (1952), 65-68.

Cochran, W., Acta Cryst. 8 (1955), 473-478.

Dewar, R. B. K., in F. R. Ahmed (ed.), Crystallographic Computing, pp. 63-65, Copenhagen, Munksgaard (1970).

Germain, G. and Woolfson, M. M., Acta Cryst. B24 (1968), 91-96.

Gillis, J., Acta Cryst. 1 (1948), 174-179.

Harker, D. and Kasper, J. S., Acta Cryst. 1 (1948), 70-75.

Hauptman, H. and Karle, J., ACA Monograph No. 3, Pittsburgh, Polycrystal Book Service (1953).

Hauptman, H., Acta Cryst. A31 (1975), 680-687.

Hauptman, H., Acta Cryst. A30 (1974), 472-477.

Karle, I. L. and Karle, J., Acta Cryst. 16 (1963), 969-975.

Karle, I. L. and Karle, J., Acta Cryst. 17 (1964), 835-841.

Karle, J., in International Tables for X-ray Crystallography, Vol. IV, Section 6, pp. 337-358, Birmingham, The Kynoch Press (1974).

Karle, J. and Hauptman, H., Acta Cryst. 3 (1950), 181-187.

Karle, J. and Hauptman, H., Acta Cryst. 9 (1956), 635-651.

Karle, J. and Karle, I. L., Acta Cryst. 21 (1966), 849-859.

Kitaigorodskii, A. I., Dokl. Acad. Nauk SSSR 94 (1954); Trudy Inst. Crystallogr. 10 (1954), 27.

Main, P., in H. Schenk, R. Olthof, H. van Koningsveld and G. C. Bassi (eds.), Computing in Crystallography, pp. 93-107, Delft, University Press (1978).

Main, P., in R. Diamond, S. Ramasheshan and K. Venkatesan (eds.), Computing in Crystallography, pp. 800-813, I. A. S., Bangalore (1980).

Overbeek, A. R. and Schenk, H., in H. Schenk, R. Olthof, H. Van Koningsveld and G. C. Bassi (eds.), Computing in Crystallography, pp. 108-112, Delft, Delft University Press (1978).

Rumanova, I. M., Dokl. Acad. Nauk. SSSR 98 (1954), 399.

Sayre, D., Acta Cryst. 5 (1952), 60-65.

Schenk, H., Transactions of the Kon. Ned. Akad. Wet, Series 1, Vol. XXV, 5, Amsterdam, London, North-Holland Publishing Company (1969).

Schenk, H., Acta Cryst. A28 (1972), 412-422.

Schenk, H., Acta Cryst. A29 (1973a), 77-82.

Schenk, H., Acta Cryst. A30 (1974), 477-482.

Schenk, H., in R. Diamond, S. Ramashan and K. Venkatesan (eds.), Computing in Crystallography, pp. 700-722, I. A. S., Bangalore (1980a).

Schenk, H., Ibid. pp. 1000-1018 (1980b).

Schenk, H., Acta Cryst. A37 (1981), 573-578.

Schenk, H. and de Jong, J. G. H. Acta Cryst. A29 (1973), 31-34.

Stewart, J. M., in F. R. Ahmed (ed.), Crystallographic Computing, pp. 71-74, Copenhagen, Munksgaard (1970).

Zachariasen, W. H., Acta Cryst. 5 (1952), 68-73.

Crystallography Matters!