Introduction to neutron powder diffractometry

E. Arzi

1. Introduction

Neutrons used in diffraction work are usually produced in a nuclear reactor by the fission of some heavy nucleus, such as ${}^{235}_{\phantom{0}92}$ U. Neutrons released in this reaction have a kinetic energy of about 5 MeV, corresponding to a de Broglie wavelength of about $1.26 \times 10^{-4}$ Å. To make these fast neutrons suitable for diffraction work, they have to be slowed down until their de Broglie wavelength becomes of the same order as the separation of atoms in condensed matter, i.e. about 1 Å. This is achieved by letting the neutrons pass through a moderator in which they gradually lose energy through a series of elastic collisions with the nuclei of the moderator. If the moderator is sufficiently thick, the neutrons emerging from it will have a Maxwellian energy distribution, their average kinetic energy being ${3\over 2}KT$ where K is the Boltzmann constant and T is the absolute temperature of the moderator. For a moderator at room temperature--i.e. for $T \approx 300$ K--this gives an average kinetic energy of about 0.04 eV, corresponding to an average neutron wavelength of about 1.5 Å (thermal neutrons).

Since the thermal neutrons emerging from the moderator form a divergent beam with a continuous wavelength distribution, whereas diffraction studies require parallel beams of neutrons with a well-defined single wavelength, the thermal neutrons have to be monochromatized and collimated first before they can be allowed to fall on the specimen under study.

2. Monochromatization

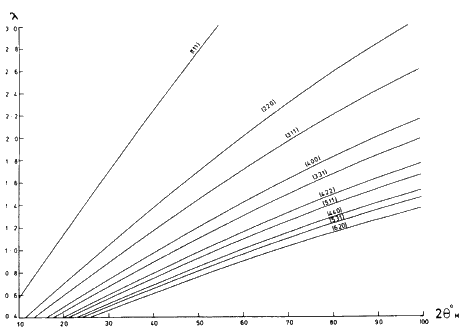
If a neutron beam with continuous wavelength distribution falls on a single crystal, various sets of lattice planes will give rise to Bragg reflections in appropriate directions, each such reflection being associated with a particular wavelength according to the Bragg law. Therefore, by aligning the single crystal appropriately with respect to the incident neutron beam, it can be achieved that only one particular wavelength will be 'reflected' in the direction required. The angle between the incident and the reflected beams is called the 'take-off angle' of the crystal monochromator. It is twice the Bragg-angle of the reflection ( $2\theta_m$ ). Figure 1 shows the wavelength vs. the take-off angle graph of a germanium crystal monochromator for different sets of reflecting planes. Large single crystals of other materials such as lead, copper, zinc, aluminium, beryllium, graphite, $\dots$ are also used as monochromators in neutron diffraction studies. They can be used either in reflection or transmission.

**Figure 1:** Wavelength *vs.* take-off angle for GF Monochromator.
$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

The reflectivity of a perfect single crystal is low caused by the large primary extinction due to the small angular misalignment of the mosaic blocks which the crystal is composed of (so-called mosaic spread, $\beta_1$ ). One way of increasing the reflectivity of a crystal monochromator is to increase the mosaic spread through a controlled and uniform distribution of imperfections such as the introduction of dislocations or impurities. The mosaic spread of a crystal monochromator can be estimated from the width-at-half-height of its 'rocking curve' which is the intensity of the reflected neutron beam plotted as a function of the angular setting of the crystal in the immediate neighbourhood of a Bragg peak.

Germanium and silicon crystals both have diamond structure, hence the second order reflections from lattice planes whose Miller indices (hkl) are all odd--such as the 222, 622 and 662 reflections--are systematically absent. Hence using the 111, 311 or 331 reflecting planes of a germanium monochromator, there will be no $\lambda/2$ contamination in the monochromated beam. Another advantage of these crystal monochromators is their low absorption and low incoherent scattering cross section. Moreover, large single crystals of germanium and silicon are readily available, though are often 'too perfect' for diffraction work resulting in a very low reflectivity. Increasing the mosaic spread by doping impurity into perfect single crystals of germanium has not been very successful. Barrett, Mueller and Heaton (1963) tried several ways of introducing imperfections into a germanium single crystal to increase its reflectivity. The best method turned out to be an uniaxial compression of a disc or slab of germanium along the [110] direction at 650 $^\circ$ C ('squashed' single crystal). This compression produced a uniform mosaic spread and a high neutron reflectivity. Barrett et al. reported an increase in the reflectivity of a compressed single crystal of germanium by a factor up to 30 as compared with the reflectivity of an 'as-grown' crystal. By varying the amount of compression, a wide range of mosaic spread can be obtained. This method proved to be quite successful and was subsequently adopted by Dolling and Nieman (1967) at Chalk River Nuclear Laboratories, Canada and by Cooper and Nathans (1967) at Brookhaven National Laboratory, USA as well as at the A.E.R.E., Harwell. (Note: Herbstein, Boonstra, Dunn, Chipman, Boldrini and Loopstra, 1967, gave a brief abstract of 520 papers published up to the end of 1966 under the heading: 'Methods of obtaining monochromatic X-rays and neutrons'. See also, Turberfield, 1968).

Some efforts have been made in recent years to develop multilayer monochromators for neutrons (see e.g. Saxena and Schoenborn, 1977). Alternating thin film of two materials such as Mn and Ge, deposited on a glass substrate, makes a periodic system in the direction normal to the plane of the multilayer with a periodicity determined by combined thickness of two films. By choosing the appropriate materials, the multilayer can give rise to very high reflectivities, and in addition to that, the diffracted beam has very low high-order contamination. According to Saxena and Schoenborn, the multilayers can also be used as excellent polarizers and filters for neutrons.

The study of curved neutron monochromators has recently attracted much attention and seems promising though not well understood as yet (see e.g. Rustichelli, 1969; Riste, 1970; Nunes and Shirane, 1971; Antonini et al., 1972; Boeuf and Rustichelli, 1973,1974; Kalus et al., 1973; Currant, 1973; Kalus, 1975; Frey, 1975; Albertini et al., 1977; Boeuf et al., 1979). A curved monochromator is either a bent single crystal or it is basically composed of bent perfect crystal slices (lamellae). The bending of the crystals is done either mechanically, chemically or thermally. The basic principles of these monochromators are the same as for the bent monochromators in X-ray experiments (see e.g. Parrish and Roberts, 1962; Herbstein et al., 1967 and Webb et al., 1977).

3. Collimation

To produce a parallel neutron beam, the monochromated neutrons have to be collimated. Neutron powder diffractometers normally use Soller slit-type collimators, named after Soller (1924) who has used this type of collimation for the first time in his X-ray experiments. Soller-slits suitable for collimating neutron beams were described by Sailor, Foote, Landon and Wood (1956). See also Poletti and Rossitto (1973).

Each collimator consists of a number of thin metal sheets (steel or brass, about 0.1 mm thick) bound together to form a series of long, narrow, rectangular channels separated by the metal sheets. Each slit (channel) allows a narrow parallel beam of neutrons to pass through. Diverging neutrons get repeatedly reflected (scattered) and absorbed by the metal sheets forming the walls of the slits. To increase absorption the metal sheets are plated with cadmium, either by spraying or by inserting them into molten cadmium (see also Meister and Weckermann, 1973 and Hey et al., 1975).

The ratio of the width to the length of a single channel of the Soller slits is called the horizontal angular divergence ( $\alpha$ ) and it is of the order of a few minutes of arc. The ratio of the height to the length of a single channel of the collimator is called the vertical divergence and it is of the order of a few degrees of arc.

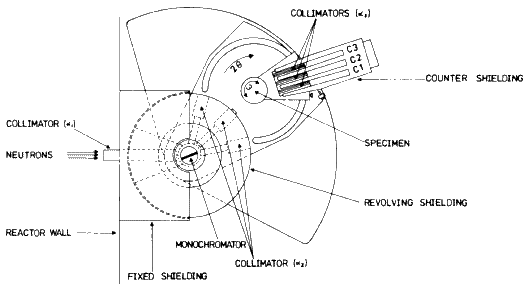
In high-resolution powder diffractometers three such Soller-slit type collimators are used in the following positions: one in front and one behind the crystal monochromator and a third one in front of the BF₃ counter (see $\alpha_1$ , $\alpha_2$ and $\alpha_3$ in Fig. 2). The $\alpha_1$ -collimator is usually called 'in-pile' and the other two 'out-pile' collimators.

Caglioti, Paoletti and Ricci (1958) calculated the width-at-half-height (WHH) and the luminosity (L) of the powder peaks as a function of the horizontal angular divergence of the three collimators ( $\alpha_1$ , $\alpha_2$ and $\alpha_3$ ) and of the mosaic spread of the crystal monochromator ( $\beta_1$ ). The effect of the vertical divergence was neglected in the calculations, since this is usually much larger than the horizontal divergence. (Note: it is worth mentioning that the effect of the vertical divergence cannot be ignored altogether since it broadens the powder peaks on their low-angle sides and thus makes them asymmetric. The amount of asymmetry depends on the Bragg angle, it is zero at $2\theta = 90^\circ$ .)

**Figure 2:** A schematic diagram of a neutron powder diffractometer named PANDA which is installed at A.E.R.E. Harwell.
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

In a subsequent paper Caglioti and Ricci (1962, see also Caglioti, 1970) compared the calculated values of WHH with the experimental ones and found a reasonably good agreement, but the calculated luminosity was normalized by an appropriate factor P to match the experimental value.

The profile $I(\rho)$ of each Bragg powder peak was found to be a Gaussian function of the following type:

$\begin{displaymath} I(\rho) = M {\alpha_1\alpha_2\alpha_3\beta_1\over N} \exp\{-4(\ln 2)\rho^2/\hbox{WHH}^2\} \eqno(1) \end{displaymath}$

where $\rho$ is the $2\theta$ -positions of the profile. $\rho = 0$ is the exact direction of the Bragg reflection and $\alpha_1$ , $\alpha_2$ and $\alpha_3$ are the horizontal angular divergences of the three collimators, $\beta_1$ is the mosaic spread of the crystal monochromator, M is a constant and WHH is the width-at-half-height of the powder peak given by the following equation:

$\begin{displaymath} \hbox{WHH} = N/(\alpha_1^2 + \alpha_2^2 +4\beta_1^2)^{l/2} \eqno(2) \end{displaymath}$

and

$\begin{displaymath} N = \{\alpha_1^2\alpha_2^2 + \alpha_1^2\alpha_3^2 + \alpha... ...2 + \alpha_1^2\beta_1^2 + \alpha_2^2\beta_1^2)\}^{1/2} \eqno(3)\end{displaymath}$

In the expression of N, $a = \tan \theta/\tan \theta_m$ where $\theta$ and $\theta_m$ are the Bragg angle of the powder peak and the take-off angle of the crystal monochromator respectively. By integrating eq. (1) with respect to the angular positions $\rho$ of the counter around the peak position ( $\rho = 0$ ) the following equation was found for the instrumental luminosity:

$\begin{displaymath} L= {\alpha_1\alpha_2\alpha_3\beta_1 \over (\alpha_1^2 + \alpha_2^2 + 4 \beta_1^2)^{1/2}} \eqno(4)\end{displaymath}$

It is important to note that L is independent of $a = \tan \theta/\tan \theta_m$ , so that no geometrical corrections originating from the collimating system are required in evaluating the structure factors from the measured integrated intensities of the powder peaks.

Caglioti et al. (1958) point out that the luminosity L is a symmetrical function of $\alpha_1$ and $\alpha_2$ but is a linear function of $\alpha_3$ so that a convenient way of obtaining larger luminosity is to increase $\alpha_3$ which broadens the diffraction peaks mainly for small 2 $\theta$ angles. Caglioti et al. also suggest that the collimator divergence angles should be chosen in such a way that $\alpha_3 \gt \alpha_2 \gt \alpha_1$ .

By using eqs. (2) and (4), Popovici (1965) carried out some calculations to achieve a good compromise between luminosity and the resolution. He points out that the optimum relation between the luminosity and WHH of powder peaks is strongly dependent on parameter $a = \tan \theta/\tan \theta_m$ ,hence it can be given only for a given peak and not for the whole powder pattern.

For relatively large values of a (higher $2\theta$ values) the calculation confirmed the result obtained earlier by Caglioti et al. (1958) for which the inequalities $\alpha_3 \gt \alpha_2 \gt \alpha_1$ must be satisfied. In the range of relatively small values of a it is necessary to eliminate the collimator between the crystal monochromator and the sample which is equivalent to $\alpha_2 = \infty$ because near the focussing point of the diffractometer the WHH of the powder peaks is insensitive to the value of $\alpha_2$ whereas larger values of $\alpha_2$ give rise to higher luminosity, see also Sakamoto et al. (1965). (Note: the D₂ neutron powder diffractometer at the ILL, Grenoble, France is operating without $\alpha_2$ -collimator as well as Panda diffractometer.)

Any misalignment or distortion of the cadmium plated steel sheets defining the Soller-slits can have a drastic effect on the value of angular divergence and hence alter the WHH and the luminosity of the powder peaks.

Another disturbing effect which was not included in the calculation of Caglioti et al. (1958) and Popvici (1965) is the total reflection of thermal and long-wavelength neutrons from the surfaces of the metal sheets of the collimators which impair the angular divergences and thus increase the WHH of the Bragg peaks. Jones and Bartolini (1963) showed that total reflection will occur for all angles of incidence less than the critical angle $\theta_c$ (which is of the order of a few minutes of arc and differs from one substance to another). They suggest that by coating the steel plates with organic compounds containing hydrogen, $\theta_c$ could be drastically reduced thus the total reflection could be suppressed. One of the most suitable coatings appears to be tetradecanoic acid (C₁₄H₂₈O₂), a very stable fatty acid, which does not absorb or adsorb gases and does not decompose even above its melting point ( $T= 53-54^\circ \hbox{C}$ ). Jones and Bartolini point out that a 1 'mil' coating of this acid reduces the total reflection by a factor of 420 due to the high incoherent scattering cross-section of hydrogen. This type of coating can only be used for the 'out-pile' collimators ( $\alpha_2$ and $\alpha_3$ ).

4. Filtering

A crystal monochromator set to reflect a chosen wavelength $\lambda$ in the direction $2\theta_m$ from a set of lattice planes (hkl) according to Bragg law does not reflect neutrons of only this $\lambda$ wavelength, but also its higher harmonics $\lambda/2, \lambda/3, \dots, \lambda/n$ giving rise to a 2nd, 3rd, $\dots$ and nth-order contamination in the monochromatized beam. To minimize this disturbance, neutron diffraction patterns are usually recorded with neutron wavelengths of about $\lambda = 1$ Å where the contribution of the higher order contaminations is negligible. On the other hand there are cases when the use of longer wavelengths is advisable, such as the investigation of complex powder patterns with many overlapping peaks. In this case the longer wavelength has the advantage that it stretches out the diffraction pattern to higher $2\theta$ -angles, thus increasing the angular separation of the adjacent peaks and improving the resolution. The practical difficulty in using longer wavelengths is that above 1 Å the intensity of the higher order contaminations (especially $\lambda/2$ )gets more pronounced. At sufficiently high wavelengths the intensity of the second-order contamination may even exceed that of the fundamental monochromatic wavelength. In such cases these higher order contaminations must be eliminated by an appropriate neutron filter. If the monochromator is a germanium single crystal and only reflections from lattice planes with three odd indices are used, the second order reflections are eliminated automatically (see Section 2). Hence in this case only the third-order contamination must be filtered out from the monochromated beam.

There are numerous neutron filters described in the literature, such as polycrystalline filters, mechanical velocity selector, resonance filter and single crystal filters. The most practical and efficient of these appear to be the polycrystalline filters, and among the single crystal filters a special crystal of graphite (so-called pyrolytic graphite). They are easy to use and have high transmission for the fundamental wavelength.

Pyrolytic graphite is a crystalline form of graphite with pronounced preferred orientation. The hexagonal c-axis is highly aligned so as to have a single crystal structure in that direction but the a-axis has a random orientation in the basal plane. If a parallel beam of neutrons passes through such a crystal parallel to the c-axis, the shorter wavelengths get scattered through Bragg reflections from the lattice planes while the longer wavelengths remain unaffected since they cannot satisfy the Bragg equation. Thus the pyrolytic graphite is transparent to longer wavelengths and opaque to shorter ones.

Figure 3 shows the total neutron scattering cross section as a function of the incident neutron energy for a collimated neutron beam having a Maxwellian energy distribution incident parallel to the c-axis of a pyrolytic graphite crystal. The figures above the peak positions are the indices of the reflecting planes (hkl) responsible for the scattering of neutrons of a particular energy (wavelength).

**Figure 3:** Total cross section per atom (in barns) *vs.* energy for pyrolytic graphite crystal aligned with the c-axis parallel to the incident white neutron beam. After Loopstra, 1966.
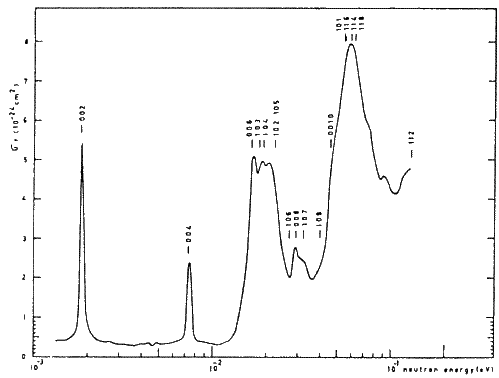$\begin{figure} \includegraphics {fig3.ps} \end{figure}$

It can be seen that below and above the 004 peak there are ranges of energies with very low scattering cross section, suggesting that pyrolytic graphite is transparent to neutrons having energies in those ranges while eliminating their higher order contaminations through scattering. Most of the investigators using pyrolytic graphite as a neutron filter were concerned with the elimination of the second-order contamination, because it was found that a sufficient size of crystal for eliminating $\lambda/2$ was always sufficient for the higher order contamination as well.

Loopstra (1966) suggested the use of a wavelength of $\lambda = 2.6$ Å for neutron powder diffractometry which has its second and third order contaminations at E = 48.4meV and 108.9 meV respectively. It can be seen from Fig. 3 that the total neutron scattering cross sections corresponding to these two energies are high suggesting that they will be filtered out. On the other hand, the total scattering cross section for the fundamental wavelength ( $\lambda = 2.6$ Å corresponding to E = 12.1 meV) is very low.

Bergsma and Van Dijk (1967) measured the total neutron scattering cross section of pyrolytic graphite at room temperature and at liquid nitrogen temperature and showed that a 4 cm thick crystal of this type was an excellent filter for the elimination of higher order contamination from a neutron beam with its primary energy in the ranges of 4-5 meV and 11-14 meV (corresponding to $\lambda = 4.52-4.04$ Å and $\lambda =2.73-2.42$ Å respectively). They also found that the transmission of the primary neutron beam with an energy of E = 13.5 meV ( $\lambda = 2.46$ Å) through a 3.8 cm thick pyrolytic graphite can be increased from 67% at room temperature to 74% by cooling it down to liquid nitrogen temperature (because cooling the crystal reduces the contribution of the thermal diffuse scattering to the total neutron scattering cross section hence increases the transmission). The second-order transmission did not change by cooling the pyrolytic graphite.

Shirane and Minkiewicz (1970) showed that the efficiency of a filter of a given thickness increases as the mosaic spread of the pyrolytic graphite decreases. The transmission ratios of the primary ( $\lambda$ ) and secondary ( $\lambda/2$ ) components for the 2 $^{\prime\prime}$ thick pyrolytic graphite filter with different mosaic spreads are given in Table 1.

Heller and Saad (1975) showed that by turning the pyrolytic graphite slightly out of position while keeping its orientation axis parallel to the incident neutron beam, the energy range for filtering can be increased and by using a graphite filter with a small mosaic spread, the loss of neutron intensity of the fundamental wavelength can be reduced for required reduction of the higher order contamination.

**Table 1:** Observed transmission ratios of 2 $^{\prime\prime}$ thick pyrolytic graphite filters for the primary neutron wavelengths of $\lambda=2.44$ Å or $\lambda = 2.34$ Å. After Shirane and Minkiewicz, 1970.
		Mosaic spread
wavelength	6.5 $^\circ$	3.5 $^\circ$	1.0 $^\circ$
$\lambda$	${1\over 2}$	${3\over 4}$	${5\over 6}$
${\lambda\over 2}$	${1\over 20}$	${1\over 1500}$	${1\over 15,000}$

Frikkee (1975) investigated the neutron transmission through a pyrolytic graphite filter as a function of the filter orientation with respect to the beam and showed that tuned pyrolytic graphite filters are useful for neutron beams having fundamental wavelength between 2.23 and 3.96 Å while cooled polycrystalline Be filters would be more efficient for wavelengths greater than 3.96 Å.

References

Arzi, E., Crystal Structure and Phase Transition in Deuteromethane (CD₄), pp. 307-314, Ph.D. Thesis, Queen Mary College, University of London (1975).

Albertini, G., Boeuf, A., Mazkedian, S., Melone, S., Rozzi, V. and Rustichelli, F., Comparison of Curved Monochromator Neutron Data with the Prediction of a Simple Model, J. Appl. Cryst. 10 (1977), 118-122.

Antonini, M., Corchia, M. and Nicotera, E., Curved Silicon Crystals as Neutron Monochromators, Nucl. Instrum. Methods. 104 (1972), 147-152.

Barrett, C. S., Mueller, M. H. and Heaton, L., Germanium as Neutron Monochromator, Rev. Sci. Instrum. 34 (8) (1963), 847-848.

Bergsma, J. and Van Dijk, C., Pyrolytic Graphite as Second-Order Neutron Filter, Nucl. Instrum. Methods. 51 (1967), 121-124.

Boeuf, A. and Rustichelli, F., Composite Focusing Neutron Monochromator System, Nucl. Instrum. Methods. 107 (1973), 429-435.

Boeuf, A. and Rustichelli, F., Some Neutron Diffraction Experiments on Curved Silicon Crystals, Acta Cryst. A30 (1974), 798-805.

Boeuf, A., Coppola, R., Melone, S., Puliti, P. and Rustichelli, F., Preliminary Theoretical Approach to the Neutron Diffraction by Bent Mosaic Crystals, Lett. Nuovo Cimento. 26 (5) (1979), 129-134.

Caglioti, G., Paoletti, A. and Ricci, F. P., Choice of Collimator for a Crystal Spectrometer for Neutron Diffraction, Nucl. Instrum. Methods. 3 (1958), 223-228.

Caglioti, G. and Ricci, F. P., Resolution and Luminosity of Crystal Spectrometers, Nucl. Instrum. Methods. 15 (2) (1962), 155-163.

Caglioti, G., Conventional and Three-Axis Neutron Powder Diffractometer, in B. M. T. Willis (ed.), Thermal Neutron Diffraction, (1970), pp. 14-33. Oxford Univ. Press.

Cooper, M. J. and Nathans, R., The Resolution Function in Neutron Diffractometry. I. The Resolution Function of a Neutron Diffractometer and its Application to Phonon Measurements, Acta Cryst. 23 (1967), 357-367.

Currant, R., The Efficiency of Vertically Bent Neutron Monochromators, Nucl. Instrum. Methods. 107 (1973), 21-28.

Dolling, G. and Nieman, H., Elimination of Second-Order Effects in Triple-Axis Crystal Spectrometer, Nucl. Instrum. Methods. 49 (1967), 117-120.

Dorner, B. and Kollmar, A., Is Pyrolytic Graphite an Ideal Mosaic Crystal?, J. Appl. Cryst. 7 (1974), 38-41.

Frey, F., Use of a Bent Packet of Perfect Crystal Lamellae as Focusing Neutron Monochromator, Nucl. Instrum. Methods. 125 (1975), 9-17.

Frikkee, F., Application of Pyrolytic Graphite as a Tunable Neutron Filter, Nucl. Instrum. Methods. 125 (1975), 307-312.

Heller, H. and Saad, M., High-Oriented Pyrolytic Graphite as Neutron Filter. Part II. Second-Order Neutron Filter. Atomkernenergie (ATKE). Bd26 (1975), 274-275.

Herbstein, F. H., Boonstra, E. G., Dunn, H. M., Chipman, D. R., Boldrini, P. and Loopstra, B. O., Methods of Obtaining Monochromatic X-Rays and Neutrons, Vol. 3, pp. 1-79, International Union of Crystallography, Commission on Crystallographic Apparatus, (1967).

Hey, P. D., Mack, B. and Carlile, C., Fine Slit Neutron Collimators Using Stretched Film. Rutherford Laboratory Report RL-75-20 (1975).

International Tables for X-ray Crystallography. Published for the Intern. Union of Cryst. by Kynoch Press, Birmingham, England. 1 (1952) Symmetry Groups, 2 (1959) Mathematical Tables, 3 (1962) Physical and Chemical Tables, 4 (1974) Revised and Supplementary Tables.

Jones, I. R. and Bartolini, W., Suppression of Total Reflection of Neutrons from Collimator Surfaces, Rev. Sci. Instrum. 34 (1) (1963), 28-30.

Kalus, J., Gobert, G. and Schedler, E., Thermally Bent Ideal Crystals as Monochromators for Neutron Scattering, J. Phys. E. 6 (1973), 488-492.

Kalus, J. Ein Gekrummter Neutronenmonochromator Hoher Reflektivitat, J. App. Cryst. 8 (1975). 361-364.

Loopstra, B. O., Neutron Powder Diffractometry Using a Wavelength of 2.6 Å, Nucl. Instrum. Methods. 44 (1966), 181-187.

Meister, H. and Weckermann, B., Neutron Collimators with Plates of Self-Contracting Foils, Nucl. Instrum. Methods. 108 (1973), 107-111.

Nunes, A. C. and Shirane, G., Vertically Bent Pyrolytic Graphite Crystals Applied to Triple-Axis Neutron Spectrometry, Nucl. Instrum. Methods. 95 (1971), 445-452.

Parrish, W. and Roberts, B. W., International Tables for X-Ray C-rystallography, Vol. III, The Kynoch Press. (1962), 73.

Poletti, G. and Rossitto, F., The Performances of Neutron Collimators. II. Choice of the Parameters of a Primary Collimator, Acta Cryst. A29 (1973), 440-444.

Popovici, M., Choice of Collimators for Neutron Powder Diffractometry, Nucl. Instrum. Methods. 36 (1965), 179-180.

Riste, T., Singly Bent Graphite Monochromators for Neutrons, Nucl. Instrum. Methods. 86 (1970), 1-4.

Rustichelli, F., Analysis of Composite Neutron Monochromator Systems Consisting of Curved Crystalline Lamellas, Nucl. Instrum. Methods. 74 (1969), 219-223.

Sabine, T. M. and Weinstock, F. V., The Influence of Collimator Geometry on Neutron Flux, J. Appl. Cryst. 2 (1969), 141-142.

Sailor, V. L., Foote, H. L. Jr., Landon, H. H. and Wood, R. E., High Resolution Crystal Spectrometer for Neutrons, Rev. Sci. Instrum. 27 (11) (1956), 26-34.

Sakamoto, M., Kunitomi, N., Motohashi, H. and Minahawa, N., Choice of Collimators for Neutron Diffraction, Japanese J. Appl. Phys. 4 (11) (1965), 911-914.

Saxena, A. M. and Schoenborn, B. P., Multilayer Neutron Monochromators, Acta Cryst. A33 (1977), 805-813.

Shirane, G. and Minkiewick, V. J., Pyrolytic Graphite as a High Efficiency Filter for 13-15 meV Neutrons, Nucl. Instrum. Methods. 89 (1970), 109-110.

Soller, W., A New Precision X-Ray Spectrometer, Phys. Rev. 24 (1924), 158-167.

Turberfield, K. C., Neutron Monochromator Studies at A.E.R.E., AERE-R 5647 (1968).

Webb, N. G., Samson, S., Stroud, R. M., Gamble, R. C. and Baldeschwieler, J. D., A Focusing Monochromator for Small-Angle Diffraction Studies with Synchrotron Radiation, J. Appl. Cryst. 10 (1977), 104-110.

...2).: The name of this diffractometer is derived from the initials of `Powder Automatic Neutron Diffraction Apparatus'. It is one of the recent neutron powder diffractometers installed at Harwell, UK and has a very high resolution. It is fitted with a mechanism which allows continuous rotation and tilting of the monochromator. By using different monochromator crystals, varying the reflecting planes and the take-off-angle, the neutron wavelength can be continuously varied from 0.5 to 4 Å. This diffractometer has a bank of three BF₃ counters in the equatorial plane (instead of one counter in simple diffractometers). Three additional counters are mounted below and another three above the equatorial counters, making a total of nine counters altogether, but the data obtained from the non-equatorial counters are not exactly the same as those for equatorial ones, see Arzi (1975). Out of three tubes marked as collimator (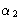) only one is used in a given diffraction experiment, the other two are blocked. The choice between the three tubes depends on the reflecting planes and the take-off-angle of the crystal monochromator.
...ones.: Highly oriented pyrolytic graphite is also used as monochromator, see e.g. Dorner and Kollmar (1974).

Crystallography Matters!