This is an archive copy of the IUCr web site dating from 2008. For current content please visit https://www.iucr.org.

3. Collimation

To produce a parallel neutron beam, the monochromated neutrons have to be collimated. Neutron powder diffractometers normally use Soller slit-type collimators, named after Soller (1924) who has used this type of collimation for the first time in his X-ray experiments. Soller-slits suitable for collimating neutron beams were described by Sailor, Foote, Landon and Wood (1956). See also Poletti and Rossitto (1973).

Each collimator consists of a number of thin metal sheets (steel or brass, about 0.1 mm thick) bound together to form a series of long, narrow, rectangular channels separated by the metal sheets. Each slit (channel) allows a narrow parallel beam of neutrons to pass through. Diverging neutrons get repeatedly reflected (scattered) and absorbed by the metal sheets forming the walls of the slits. To increase absorption the metal sheets are plated with cadmium, either by spraying or by inserting them into molten cadmium (see also Meister and Weckermann, 1973 and Hey et al., 1975).

The ratio of the width to the length of a single channel of the Soller slits is called the horizontal angular divergence ($\alpha$) and it is of the order of a few minutes of arc. The ratio of the height to the length of a single channel of the collimator is called the vertical divergence and it is of the order of a few degrees of arc.

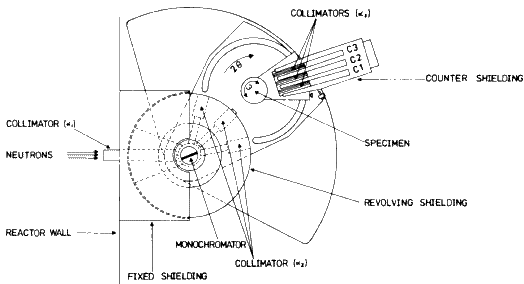
In high-resolution powder diffractometers three such Soller-slit type collimators are used in the following positions: one in front and one behind the crystal monochromator and a third one in front of the BF₃ counter (see $\alpha_1$, $\alpha_2$ and $\alpha_3$ in Fig. 2). The $\alpha_1$-collimator is usually called `in-pile' and the other two `out-pile' collimators.

Caglioti, Paoletti and Ricci (1958) calculated the width-at-half-height (WHH) and the luminosity (L) of the powder peaks as a function of the horizontal angular divergence of the three collimators ($\alpha_1$,$\alpha_2$ and $\alpha_3$) and of the mosaic spread of the crystal monochromator ($\beta_1$). The effect of the vertical divergence was neglected in the calculations, since this is usually much larger than the horizontal divergence. (Note: it is worth mentioning that the effect of the vertical divergence cannot be ignored altogether since it broadens the powder peaks on their low-angle sides and thus makes them asymmetric. The amount of asymmetry depends on the Bragg angle, it is zero at $2\theta = 90^\circ$.)

 

Figure 2: A schematic diagram of a neutron powder diffractometer named PANDA which is installed at A.E.R.E. Harwell.

In a subsequent paper Caglioti and Ricci (1962, see also Caglioti, 1970) compared the calculated values of WHH with the experimental ones and found a reasonably good agreement, but the calculated luminosity was normalized by an appropriate factor P to match the experimental value.

The profile $I(\rho)$ of each Bragg powder peak was found to be a Gaussian function of the following type:

$$I(\rho) = M {\alpha_1\alpha_2\alpha_3\beta_1\over N} \exp\{-4(\ln 2)\rho^2/\hbox{WHH}^2\} \eqno(1)$$

where $\rho$ is the $2\theta$-positions of the profile. $\rho = 0$ is the exact direction of the Bragg reflection and $\alpha_1$, $\alpha_2$ and $\alpha_3$ are the horizontal angular divergences of the three collimators, $\beta_1$ is the mosaic spread of the crystal monochromator, M is a constant and WHH is the width-at-half-height of the powder peak given by the following equation:

$$\hbox{WHH} = N/(\alpha_1^2 + \alpha_2^2 +4\beta_1^2)^{l/2} \eqno(2)$$

and

$$N = \{\alpha_1^2\alpha_2^2 + \alpha_1^2\alpha_3^2 + \alpha... ...2 + \alpha_1^2\beta_1^2 + \alpha_2^2\beta_1^2)\}^{1/2} \eqno(3)$$

In the expression of N, $a = \tan \theta/\tan \theta_m$ where $\theta$ and $\theta_m$ are the Bragg angle of the powder peak and the take-off angle of the crystal monochromator respectively. By integrating eq. (1) with respect to the angular positions $\rho$ of the counter around the peak position ($\rho = 0$) the following equation was found for the instrumental luminosity:

$$L= {\alpha_1\alpha_2\alpha_3\beta_1 \over (\alpha_1^2 + \alpha_2^2 + 4 \beta_1^2)^{1/2}} \eqno(4)$$

It is important to note that L is independent of $a = \tan \theta/\tan \theta_m$, so that no geometrical corrections originating from the collimating system are required in evaluating the structure factors from the measured integrated intensities of the powder peaks.

Caglioti et al. (1958) point out that the luminosity L is a symmetrical function of $\alpha_1$ and $\alpha_2$ but is a linear function of $\alpha_3$ so that a convenient way of obtaining larger luminosity is to increase $\alpha_3$ which broadens the diffraction peaks mainly for small 2$\theta$ angles. Caglioti et al. also suggest that the collimator divergence angles should be chosen in such a way that $\alpha_3 \gt \alpha_2 \gt \alpha_1$.

By using eqs. (2) and (4), Popovici (1965) carried out some calculations to achieve a good compromise between luminosity and the resolution. He points out that the optimum relation between the luminosity and WHH of powder peaks is strongly dependent on parameter $a = \tan \theta/\tan \theta_m$,hence it can be given only for a given peak and not for the whole powder pattern.

For relatively large values of a (higher $2\theta$ values) the calculation confirmed the result obtained earlier by Caglioti et al. (1958) for which the inequalities $\alpha_3 \gt \alpha_2 \gt \alpha_1$must be satisfied. In the range of relatively small values of a it is necessary to eliminate the collimator between the crystal monochromator and the sample which is equivalent to $\alpha_2 = \infty$because near the focussing point of the diffractometer the WHH of the powder peaks is insensitive to the value of $\alpha_2$ whereas larger values of $\alpha_2$give rise to higher luminosity, see also Sakamoto et al. (1965). (Note: the D₂ neutron powder diffractometer at the ILL, Grenoble, France is operating without $\alpha_2$-collimator as well as Panda diffractometer.)

Any misalignment or distortion of the cadmium plated steel sheets defining the Soller-slits can have a drastic effect on the value of angular divergence and hence alter the WHH and the luminosity of the powder peaks.

Another disturbing effect which was not included in the calculation of Caglioti et al. (1958) and Popvici (1965) is the total reflection of thermal and long-wavelength neutrons from the surfaces of the metal sheets of the collimators which impair the angular divergences and thus increase the WHH of the Bragg peaks. Jones and Bartolini (1963) showed that total reflection will occur for all angles of incidence less than the critical angle $\theta_c$ (which is of the order of a few minutes of arc and differs from one substance to another). They suggest that by coating the steel plates with organic compounds containing hydrogen, $\theta_c$ could be drastically reduced thus the total reflection could be suppressed. One of the most suitable coatings appears to be tetradecanoic acid (C₁₄H₂₈O₂), a very stable fatty acid, which does not absorb or adsorb gases and does not decompose even above its melting point ($T= 53-54^\circ \hbox{C}$). Jones and Bartolini point out that a 1 `mil' coating of this acid reduces the total reflection by a factor of 420 due to the high incoherent scattering cross-section of hydrogen. This type of coating can only be used for the `out-pile' collimators ($\alpha_2$ and $\alpha_3$).

Copyright © 1984, 1997 International Union of Crystallography