This is an archive copy of the IUCr web site dating from 2008. For current content please visit https://www.iucr.org.

(1) Cas du réseau primitif

Pour simplifier on considère d'abord uniquement le cas du réseau primitif qui est celui en Fig. 1 et 2, où on trouve une seule fleur par maille (4 situées aux 4 coins qui comptent pour $\frac{1}{4}$. Mais on distingue 2 cas:

Cas de la Fig. 1: On a une fleur par maille et on doit la dessiner entièrement pour définir une maille, donc tout le cristal.

Cas de la Fig. 2: On a une fleur par maille mais il suffit de n'en dessiner qu'un quart, par exemple $\mathcal{P}$, si on précise que dans le rectangle maille de la Fig. 2 (i) on a des axes de rotation d'ordre 2 (rotations 0, $\Pi$) aux coins de la maille, aux milieux des côtés et des centres de celle-ci; (ii) on a des plans de symétrie, ou miroirs, qui se projettent orthogonalement sur le côté de la maille et sur les droites parallèles aux côtés passant par le centre. Cf. Fig. 2

axe 2 ($\perp$ au dessin); -miroir ($\perp$ au dessin)

on note bien que pour le cristallographe les quatre quarts de fleur hachurés sont strictement équivalent et ne constituent qu'un seul et même objet de l'ensemble quotient E/T qu'on appelle la maille.

On est donc conduit à rechercher les opérations ponctuelles de symétries (O.P.S.) qui laissent une fleur inchangée. Il s'agit d'isométries ponctuelles , opérations qui conservent les longeurs, ainsi que le centre de la fleur.

On raisonne par exemple, sur la fleur située en 0 et on trouve quatre O.P.S.:

e , 1$^{\prime}$ identité représentée par la matrice 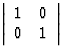à déterminant + 1

2, la rotation $\Pi$ représentée par la matrice 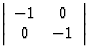à déterminant + 1

m₁, la symétrie par rapport à Ox représentée par la matrice 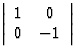à déterminant -1

m₂, la symétrie par rapport à Oy représentée par la matrice 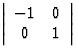à déterminant -1

Théorème : ces quatre O.P.S. (ou les matrices orthogonales 2 $\times$ 2 qui leur correspondent) constituent un groupe ponctuel de symétrie (G.P.S.), d'ordre 4 et noté 2mm.

Démonstration : établissons la table de multiplication

- la multiplication est une loi de composition interne dans l'ensemble e, 2, m₁, m₂

- chaque élément est lui même son propre inverse

- le produit de deux éléments différents de e donne le troisième élément différent de e

- il s'agit donc d'un groupe isomorphe au groupe de Klein

$$\begin{array} {lllll} & e & 2 &m_1 & m_2 \\ e & e & 2 &m_1... ...\\ m_1 & m_1& m_2 & e & 2 \\ m_2 & m_2& m_1& 2 & e\end{array}$$

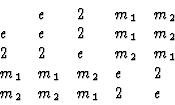
ceci signifie que dans un cristal à deux dimensions dont le G.P.S. est 2mm, chaque fois qu'on précise un point du contour de la fleur par ses coordonnées xy on sait qu'il y a forcément trois autres points dont les coordonnées sont $\overline{x}\,\overline{y}$, $x\overline{y}$, $\overline{x}y$.

Definition : l'ensemble de ces quatre points s'appelle les 4 positions générales de Wyckoff du cristal et il y a évidemment isomorphisme entre les quatre transformations

$$xy \rightarrow xy; xy \rightarrow \overline{x}\,\overline{y}; xy \rightarrow x\overline{y}; xy \rightarrow \overline{x}y$$

et les quatre O.P.S. du G. P. S. 2mm: e, 2, m₁, m₂.

Conclusion : sauf dans un cas particulier comme celui de la Fig. 1 où le G.P.S. du cristal se réduit à l'O.P.S. identité, il est donc indispensable de connaitre le G.P.S. d'un cristal , c'est-à-dire les O.P.S. qui conservent globalement le motif constituant la maille (ensemble quotient E/T) d'un réseau primitif. Les O.P.S. sont donc obligatoirement des isométries ponctuelles.

Il suffit alors de décrire un quart de la maille (dans le cas de 2mm) pour la connaitre toute .

Dans les cristaux réels on a des atomes ou des ions. On peut d'abord simplifier le problème en le ponctualisant sur leur noyau qu'on assimile à un point. Si le G.P.S. du cristal est 2mm (supposons qu'il s'agisse d'une monocouche chimisorbée, véritable cristal à deux dimensions) cela signifie que si un atome d'oxygène est en position générale de Wyckoff (x et y $\neq$ 0) on a forcément 4 atomes d'oxygène dans la maille et les positions des trois autres sont impérativement fixées par la position du premier. Dans le quart de maille il suffira donc de préciser la position d'un nombre fini de noyaux d'atomes ou d'ions.

Si on veut être plus précis il faudra établir dans le quart de la maille une carte de densité électronique à partir de laquelle on déduit immédiatement la densité électronique dans les trois autres quarts de la maille.

Copyright © 1981, 1998 International Union of Crystallography