Next: References Up: Crystal Structure Analysis Using the `Superposition' Previous: 3. Steps of Structure Determination
![[IUCr Home Page]](/iucr-top/logos/iucrhome.gif)
![[Commission Home Page]](/iucr-top/logos/cteach.gif)
![]()
![]()
![]()
Next: References
Up: Crystal Structure Analysis Using the `Superposition'
Previous: 3. Steps of Structure Determination
A. Demissidine hydroiodide8
Crystal data: C27H45NO.HI.![]() C2H5OH
C2H5OH
orthorhombic: P212121; a = 23.0 Å, b = 7.6 Å, c = 16.0 Å; Z = 4
Observed systematic intensity distribution:
![]()
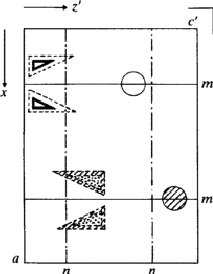
According to the chemical formula and number of molecules per unit cell there are 4 heavy atoms per unit cell, i.e. one per asymmetric unit. Thus the 2 heavy atoms related by a shift of c/2 (on account of systematic intensity distribution) must necessarily belong to the same set of equipoints. This results if and only if the atoms lie on screw dyads parallel to c (see Fig. 5), thus the set of equipoints in P212121
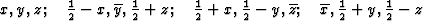
specializes to
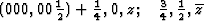
With ![]() this corresponds within the unit cell
this corresponds within the unit cell ![]() ,
, ![]() ,
, ![]() of the superposition structure, to the
equipoints
of the superposition structure, to the
equipoints
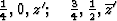
Obviously (Fig. 5), any of these two points lies on mirror planes perpendicular
to ![]() and
and ![]() and are related by an n-glide plane
perpendicular to
and are related by an n-glide plane
perpendicular to ![]() . Thus the space group of the superposition
structure is Pmmn.
. Thus the space group of the superposition
structure is Pmmn.
 |
|
The same result could have been obtained by scanning the orthorhombic higher
symmetry group for such equipoints. Then the set of special positions (a)
00z,![]() would be found for Pmmn, which corresponds to
the set found, after a shift of the origin by
would be found for Pmmn, which corresponds to
the set found, after a shift of the origin by ![]() /4.
/4.
The space group for the superposition structure thus obtained may now be tested with the usual space group tests, and indeed, the hk0-reflections with h + k = 2n + 1 are weak (corresponding to the n-glide plane). The superposition structure thus contains for each of 4 symmetry related atoms (x, y, z) etc., of the real structure the following sets of 4 atoms.
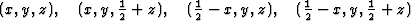
i.e. 4 atoms to any atom of the real structures. This superposition structure would be obtained, if the usual heavy atom technique could be applied, and would certainly be difficult to interpret.
The Patterson function gave, however, not only the z-coordinate of the heavy atom but also hinted that it may not lie exactly on the dyad screw, but only approximately so; this was confirmed by the Patterson of the complementary structure, obtained from the reflections with l = 2n + 1.
This indicated a deviation of xj from ![]() , and this deviation
results in contribution of reflections with high values of h which even
determine their phases.
, and this deviation
results in contribution of reflections with high values of h which even
determine their phases.
The iodine parameters were refined and with the resulting phases a first Fourier synthesis of the complementary structure was obtained in space group P212121.
This result was compared with the known part of the model and thus a part of the structure deduced and used as a starting point for the final determination of the real structure.
B. Piperidino-acet-m-bromo-anilide9
Crystal data: C13H17N2OBr
orthorhombic: Pbca; a = 23.65 Å, b = 12.66 Å, c = 9.37 Å; Z = 8
Observed systematic intensity distribution:
![]()
Space group of ![]() : Pbcm with lattice parameters
: Pbcm with lattice parameters
The 3-dimensional Patterson function explained the systematic distribution in
the intensities by the particular position of the bromine-atom on the a-glide
plane with the fractional coordinates x = 0.159, y = 0.193, z = 0.25.
With the known position of the bromine atom (refined by least squares methods)
the signs of most of the ![]() but not of the
but not of the
![]() were determined.
were determined.
With ![]() a 3-dimensional Fourier synthesis of the
superposition structure was calculated. This
a 3-dimensional Fourier synthesis of the
superposition structure was calculated. This ![]() involves
perpendicular to c an additional mirror plane, not existing in the real
structure, through the bromine atom. That is why each maximum in the synthesis
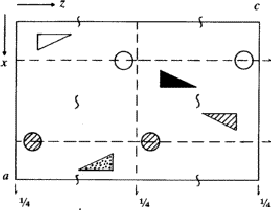
has a corresponding reflected one (Fig. 6). But only one of these pairs
corresponds to an atom in the real structure. In addition many maxima occurred
in the Fourier synthesis which do not refer to atoms. Therefore the
interpretation of the synthesis by the model of the molecule failed.
involves
perpendicular to c an additional mirror plane, not existing in the real
structure, through the bromine atom. That is why each maximum in the synthesis
has a corresponding reflected one (Fig. 6). But only one of these pairs
corresponds to an atom in the real structure. In addition many maxima occurred
in the Fourier synthesis which do not refer to atoms. Therefore the
interpretation of the synthesis by the model of the molecule failed.
To preclude the spurious peaks in the Fourier synthesis a spatial minimum function M4(x, y, z)10 was derived from the Patterson function by using the known bromine-bromine vectors.
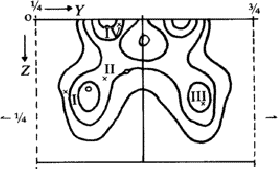
The comparison of Fourier synthesis and minimum function revealed to which of
the pairs of peaks connected by the mirror plane atoms could be assigned. These
peaks of the superposition structure are shown in Fig. 7. Its
(x, y)-projection is identical with the projection of the real structure.
A model of the molecule enabled us to determine the z-coordinates of
the atoms by eliminating the ambiguity in the Fourier synthesis.
C. Acetamide hemihydrobromide11,12
Crystal data: (CH3CONH2)2.HBr
monoclinic: P21/c, a = 6.51 Å, b = 8.64 Å, c = 8.24 Å,
![]() = 113.1
= 113.1![]() ; Z = 2
; Z = 2
![]()
From Z = 2 and P21/c it follows that the bromine atom lies at the centre of
symmetry forming, taken by themselves, an A-centred lattice. The
![]() correspond to a superposition structure with the
space group A 2/m, which has a mirror plane perpendicular b in
addition to the space group of the real structure.
correspond to a superposition structure with the
space group A 2/m, which has a mirror plane perpendicular b in
addition to the space group of the real structure.
![]()
and
![]()
where K is the scaling factor. The expressions
![]() and
and
![]() may be calculated
because xj and zj are known, whereas K cos 2
may be calculated
because xj and zj are known, whereas K cos 2![]() =
= ![]() and K sin 2
and K sin 2![]() =
= ![]() are the unknown values. From the known
position of the heavy atom (bromine) most of the signs of the F(h1l)l=2n+1
could be determined and a system of equations (4.1) with a twelvefold
overdetermination could be set up
are the unknown values. From the known
position of the heavy atom (bromine) most of the signs of the F(h1l)l=2n+1
could be determined and a system of equations (4.1) with a twelvefold
overdetermination could be set up
| (4.1) |
This system of equations was solved by least squares technique. Because the
F(h1l) are on a relative scale the solutions ![]() were multiplied
with a constant (1/K) so that (1/K)
were multiplied
with a constant (1/K) so that (1/K)![]() = 1 is valid.
= 1 is valid.
Two values yj = yjo and yj = 1 - yjo are in keeping with the
solutions Cj = (1/K)![]() (yjo) obtained. To find out which of
these two values is correct, equations of the type (4.2):
(yjo) obtained. To find out which of
these two values is correct, equations of the type (4.2):
| (4.2) |
were used. The bromine atoms do not contribute to the F(h1l)j=2n. The
signs of these structure factors were unknown. Therefore the unobserved
reflections F(h1l)l=2n and one strong reflection F(h1l)l=2n were used
for setting up a system of inhomogeneous equations. The Sj =
(1/k)![]() were less accurate than the Cj because this system of
equations had only a twofold overdetermination. That is why the absolute values
of the y-coordinates were calculated from the Cj, but the ambiguity was
eliminated by the Sj. The results are shown in Fig. 9. Structure refinement
proved these approximate values to be correct.
were less accurate than the Cj because this system of
equations had only a twofold overdetermination. That is why the absolute values
of the y-coordinates were calculated from the Cj, but the ambiguity was
eliminated by the Sj. The results are shown in Fig. 9. Structure refinement
proved these approximate values to be correct.
 |
D. ![]() -Calcium tetraborate hydrate13
-Calcium tetraborate hydrate13
Crystal data: CaB2O4.4H2O
monoclinic: Pc or P2/c, a = 5.86 Å, b = 6.93 Å, c = 7.78
Å, ![]() = 94
= 94![]() ; Z = 2
; Z = 2
Observed systematic intensity distribution:
![]()
The intensity statistic of Howells, Phillips and Rogers14 using the I(hkl) showed that the real structure has the centrosymmetric space group P2/c.
The Patterson function showed in agreement with Z = 2 and P2/c that the
calcium atom occupies a special position on the twofold rotation axis with
parameters ![]() = 0,
= 0, ![]() =
= ![]() and
and ![]() approximately
zero. This position is near the c-glide plane and thus explains why the
reflections I(hkl)l=2n+1 are systematically weak.
approximately
zero. This position is near the c-glide plane and thus explains why the
reflections I(hkl)l=2n+1 are systematically weak.
On the other hand the calcium atom determined most of the signs of the F(hk0).
The Fourier projection ![]() gave the positions of the oxygen and boron
atoms. Because the signs of the F(hkl) with l = 2n + 1 were not determined
by the contribution of the calcium atom the z-parameters of the atoms could
not be derived from a Fourier synthesis based on the contributions of the
calcium atom to the sign of the F(hkl). But with the SFE-method the
approximate z-coordinates were easily obtained.
gave the positions of the oxygen and boron
atoms. Because the signs of the F(hkl) with l = 2n + 1 were not determined
by the contribution of the calcium atom the z-parameters of the atoms could
not be derived from a Fourier synthesis based on the contributions of the
calcium atom to the sign of the F(hkl). But with the SFE-method the
approximate z-coordinates were easily obtained.
From the structure factor formula follows
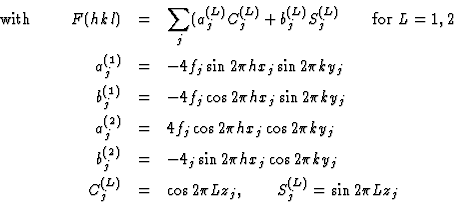
Two systems of equations were set up. For the first system F(hk1) and for the second F(hk2) were used. In each case the unobserved structure factors and one strong structure factor with arbitrary sign was used. These systems of equations gave approximate values for C(L)j and S(L)j, by which Fc(hkl) were calculated.
By comparing the Fc(hkl) with the Fo(hkl) the signs of more structure factors could be determined. The corresponding equations were added to the previous systems of equations. In this way the overdetermination of the systems of equations was increased and the accuracy of the results improved. The final results obtained after several cycles are listed in the Table. The last column contains the refined parameter for comparison.
| Atom | C(1)j | S(1)j | C(2)j | S(2)j | zj | zj refined |
| Ca | - | 1.00 | -1.000 | - | 0.250 | 0.25 |
| O1 | - | 0.20 | 0.872 | - | 0.036 | 0.0359 |
| O2 | 1.00 | 0.51 | 0.703 | 0.756 | 0.070 | 0.0588 |
| O3 | 0.68 | 0.44 | 0.111 | 0.923 | 0.106 | 0.1042 |
| O4 | -0.66 | -0.74 | -0.338 | 0.680 | 0.842 | 0.8193 |
E. Dimethylaminomethylpinene12,15
Crystal data: C13H24NBr
monoclinic: P21, a = 11.37 Å, b = 8.62 Å, c = 7.48 Å,
![]() = 97.4; Z = 2
= 97.4; Z = 2
The x- and z-parameters of the bromine atom were determined from the
Patterson synthesis and refined by Fourier methods. The y coordinate was
chosen arbitrarily as ![]() . The 3-dimensional Fourier
synthesis based on the phases of the
. The 3-dimensional Fourier
synthesis based on the phases of the ![]() derived from the bromine
contributions is a superposition structure with the space group P21/m with an
additional mirror plane at
derived from the bromine
contributions is a superposition structure with the space group P21/m with an
additional mirror plane at ![]() . For the calculation of this
synthesis only Fo(hkl) for 0k4 were available because the crystals were
very small. The Fourier synthesis revealed the positions of all non-hydrogen
atoms, most of them resolved in the x and z directions. Nearly all these
atoms, however, located so closely to the pseudo mirror plane that the peak
corresponding to one atom and its mirror image were not separated but formed an
elliptical maximum with its peak on the mirror plane (Fig. 10).
. For the calculation of this
synthesis only Fo(hkl) for 0k4 were available because the crystals were
very small. The Fourier synthesis revealed the positions of all non-hydrogen
atoms, most of them resolved in the x and z directions. Nearly all these
atoms, however, located so closely to the pseudo mirror plane that the peak
corresponding to one atom and its mirror image were not separated but formed an
elliptical maximum with its peak on the mirror plane (Fig. 10).
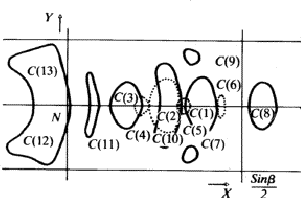 |
The main problem of the structure determination was to determine the small deviations of the light atoms from this pseudo mirror plane.
Analysis of the peak shape resulted in rather inaccurate values of the deviations from the mirror plane. Better values were obtained by the SFE method. To start with, the positions of all atoms in (x, z)-projection were refined by difference Fourier synthesis to an R value of 0.16. Using the formulae
![]()
and
![]()
where K1 and K2 are the scaling factors, two systems of equations were
obtained taking Ao(hkl) equal to Fo(hkl). This may be done without
creating large errors since the Bo(hkl), to which the bromine atoms do not
contribute, are expected to be small. In these systems of equations only those
Ao(hkl) were used whose signs could be deduced from the contributions
![]() of the bromine atoms.
of the bromine atoms.
With the abbreviations
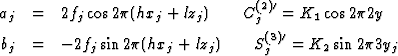
the systems of the equations have the form
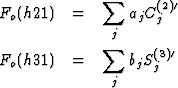
The structure factors Fo(h21) and Fo(h31) are on a relative scale. The
scaling factors K1 and K2 were given such values that
(1/K1)![]() = (1/K2)
= (1/K2)![]() = 1. Four values for the
coordinate yj of any atom are in keeping with
= 1. Four values for the
coordinate yj of any atom are in keeping with
![]()
Two of these values for any atom could be excluded by comparison with the Fourier synthesis of the superposition structure (see above). From the two remaining values one could be precluded for most of the atoms by using a model of the molecule (Fig. 10). The accuracy of the y coordinates obtained from the C(2)j was improved using the results obtained from S(3)j. The coordinates thus obtained were sufficiently accurate for a starting set for a least squares refinement of the real structure.
Copyright © 1981, 1998 International Union of Crystallography
IUCr Webmaster