Integration of direct methods with macromolecular crystallographic techniques
C. GiacovazzoDipartimento Geomineralogico, Universita' di Bari, Campus Universitario, Via Orabona 4, 70125 Bari, Italy.
criscg01@area.ba.cnr.it D. Siliqi
Dipartimento Geomineralogico, Universita' di Bari, Campus Universitario, Via Orabona 4, 70125 Bari, Italy ,
Department of Inorganic Chemistry, Tirana University, Tirana, Albania
crisds06@area.ba.cnr.it a
http://www.ba.cnr.it/~crisds06/ J. Gonzalez-Platas
Departamento de Fisica Fundamental y Experimental, Universidad de La Laguna, E-38203 La Laguna, Tenerife. Spain.
javiergp@axil320.dfis.ull.es
Abstract
The role of direct methods in macromolecular crystallography is discussed. The common belief that such methods will still remain marginal is rejected. Different sectors are analyzed. A direct procedure for phasing reflections when diffraction data of one isomorphous derivative are available is briefly described. The applications to experimental data of some test structures succeeded, and suggest that direct methods are competitive with traditional SIR techniques. Attention is also devoted to a formula which is able to recover the total from a partial structure.Direct methods can play a central role also for expanding (and refining) phases from derivative to native resolution, and can constitute an alternative to traditional molecular replacement techniques.
1 Introduction
The use of traditional direct methods for solving macromolecular crystal structures or for refining phases was initiated several years ago. It was soon realized that Sayre equation, tangent formula, Karle-Hauptman determinants, etc., even if useful in favorable conditions, were, in general, not competitive with the highly efficient techniques specifically devoted to macromolecular crystallography. The role of direct methods in this area seemed to remain quite marginal until, about two decades ago, a more fruitful integration with macromolecular crystallographic techniques involving isomorphous derivative data started [1]. However, in spite of the extensive theoretical efforts, the practical results were unsatisfactory: while theoretical phase distributions worked fine with calculated (error-free) data, they failed when applied to experimental data. It was claimed that direct methods are too sensitive to experimental errors: indeed they estimate single-phase relationships which, if incorrectly evaluated because of lack of isomorphism or errors in measurements, etc., can disturb in a destructive way the phasing process. This belief has been recently proved wrong: in a series of papers [2], [3], [4], [5], [6] a direct procedure has been described which is able to satisfactorily phase protein reflections provided diffraction data of one isomorphous derivative are available. We will synthesize in this paper the principia of the above series of papers and the main results achieved.Direct methods can do much more for macromolecular crystallography. Triplet phase distributions in the presence of anomalous dispersion effects have been independently derived by Hauptman [7] and by Giacovazzo [8]: they should constitute a useful tool for the efficient phasing of proteins even if a robust procedure is not yet available. For brevity this topic will not be treated in this paper. We will devote the last part of this article to two important sectors of the phasing process:
1) phase refinement and extension. We will shortly describe: a) the results of an innovative solvent flattening program which has been coupled with our direct methods program; b) the use of a formula proposed by Giacovazzo [9] which takes into account the prior information on a partial structure;
2) The use of direct methods for the translation of a model molecule as an alternative to traditional molecular replacement techniques.
2 Symbols and abbreviations
Symbols and notations are basically the same as in a recent series of papers [2], [3], [4], [10], [5], [6] (quoted here as papers I-VI). For the readers convenience they are listed below.Fp = |Fp|exp(i) Structure factor of the protein
Fd = |Fd|exp(i) Structure factor of the isomor- phous derivative
FH = Fd-Fp Structure factor of the heavy-atom structure (i.e. the atoms added to the native protein)
![]()
Ep = R exp(i) Normalized structure factor of the protein
Ed = S exp(i) Normalized structure factor of the isomorphous derivative
Np Number of non-H atoms in the primitive unit cell for the native protein
NH Number of heavy-atoms in the primitive unit cell for the derivative
![]() Zj = atomic number of the jth atom
Zj = atomic number of the jth atom
![]() (Statistically equivalent) num-ber of atoms in the primitive unit cell
(Statistically equivalent) num-ber of atoms in the primitive unit cell
![]() Value of Neq for the native protein
Value of Neq for the native protein
![]() Value of Neq for the heavy atom structure
Value of Neq for the heavy atom structure
fj Atomic scattering factor of the jth atom
![]() The sum is extended to the native protein atoms
The sum is extended to the native protein atoms
![]() The sum is extended to the heavy atom structure
The sum is extended to the heavy atom structure
![]() The sum is extended to the derivative atoms
The sum is extended to the derivative atoms
![]() Ii = modified Bessel function of order i
Ii = modified Bessel function of order i
![]()
![]() Derivative pseudonormalized structure factor
Derivative pseudonormalized structure factor
![]()
![]() Native pseudonormalized structure factor
Native pseudonormalized structure factor
![]() ,
, ![]()
![]()
![]() Structure factor of a partial structure
Structure factor of a partial structure
![]() (Statistically equivalent) number of atoms of the partial structure for the primitive unit cell.
(Statistically equivalent) number of atoms of the partial structure for the primitive unit cell.
![]() (Statistically equivalent) number of atoms of the difference structure obtained by subtracting the partial from the protein structure.
(Statistically equivalent) number of atoms of the difference structure obtained by subtracting the partial from the protein structure.
![]() Structure factor of the protein structure pseudo-normalized with respect to the difference structure.
Structure factor of the protein structure pseudo-normalized with respect to the difference structure.
![]() Structure factor of the partial structure pseudo-normalized with respect to the difference structure.
Structure factor of the partial structure pseudo-normalized with respect to the difference structure.
APP Avian pancreatic polypeptide [11].
BPO Bacterial haloproxidase from Streptomyces aurefaciens [12].
E2 Catalitic domain of Azoto-bacter vinlandii dihydrolipoyl transacetylase [13].
M-FABP Recombinant human muscle fatty-acid-binding protein [14].
NOX NADH oxidase from Thermus thermophilus [15].
The relevant parameters characterizing the diffraction data of our test structures are given in Table 1.
3 Direct methods and isomorphous replacement techniques
The integration of direct methods with isomorphous replacement techniques (SIR case) was first accomplished by Hauptman [1]. His main result was the following: the triplet phase invariant was estimated via a von Mises distribution whose concentration parameter is a complicated expression involving the six moduli Rh, Rk,, Rh-k, Sh, Sk, Sh-k. The first application of the method to error-free data was successful [16] but subsequent tests on real diffraction data were unsatisfactory. The weakness (and the strength) of the method was clearly outlined by Fortier, Weeks & Hauptman [17]: the accuracy of the distribution depends on the scattering difference between the native protein and the derivative. Heavy errors in the estimate of such differences heavily reduce the efficiencyof the phasing process. The problem was reconsidered by
Table 1 Relevant parameters for the diffraction data of our test structures. NREFL is the number of measured reflections up to the resolution RES for the native and derivative structures.
Native Derivative
Structure code RES(Å) NREFL Heavy atom 2H/2p RES(Å) NREFL
APP 0.99 17058 Hg 0.055 2.00 2086
BPO 2.35 23956 Au 0.028 2.78 15741
E2 2.65 10391 Hg 0.021 3.00 9179
M-FABP 2.14 7595 Hg 0.015 3.00 7125
NOX 3.00 4295 Pt 0.041 3.00 4295
Giacovazzo, Cascarano & Zheng [18]: the distribution
![]()
![]() (1)
(1)
was obtained for the case "native heavy-atom derivative", where
![]()
![]() (2)
(2)
and ![]() is the pseudo-normalized difference (with respect to the heavy-atom structure). Since
is the pseudo-normalized difference (with respect to the heavy-atom structure). Since ![]() , the Cochran parameter is often negligible with respect to the term including pseudonormalized differences: this last may attain large values even for large proteins. Since
, the Cochran parameter is often negligible with respect to the term including pseudonormalized differences: this last may attain large values even for large proteins. Since ![]() , may be positive or negative, positive as well as negative triplets can be identified via (2).
, may be positive or negative, positive as well as negative triplets can be identified via (2).
Papers I-VI were devoted to describing a procedure for phasing, via distribution (1), all the reflections up to derivative resolution. The procedure succeeded with experimental data and may be described in a few steps.
3.1 Normalization step
The standard Wilson method is applied to native protein data (up to native resolution) to obtain the scale factor Kp and the overall thermal factor Bp. Estimates of the corresponding factors for the derivative are obtained by a differential Wilson plot [19] through the equation![]()
![]() (3)
(3)
Actually from (3) the ratio Rk=Kd/Kp and the difference B=Bd-Bp are obtained. Then Bd and Kd are set to Bd=Bp+B and Kd=KpRk. Equation (3) is not sufficient for a correct rescaling of derivative data on protein data: some supplementary steps are needed. Since
![]()
one should expect that
![]() .
.
Therefore the values are rescaled by the factor
![]() (4)
(4)
to make the experimental distribution of ![]() closer to the expected one.
closer to the expected one.
The application of (4) does not guarantee a good rescaling mostly when the derivative resolution is equal to or lower than 4 . A big improvement was obtained when the scaling was performed by exploiting the P() distribution (see papers III and V). From the joint probability distribution
![]()
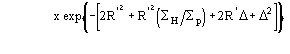
![]()
one obtains
![]() (5a)
(5a)
for positive values of and
![]() (5b)
(5b)
for negative value of Δ (the limits of integration are because ![]() has to be positive).
has to be positive).
The distribution P(Δ) has been calculated (see paper III) by numerical methods: we show in Fig.1 curves corresponding to various values of ![]() .
.
Let us now show how P(Δ) can be used in the normalizing process. Let ΔT be a positive threshold for Δ, ![]() be the number of positive Δ's for which Δ> ΔT ,
be the number of positive Δ's for which Δ> ΔT , ![]() be the number of negative Δ for which |Δ|>ΔT. Since P(Δ) is not an even function, the ratio
be the number of negative Δ for which |Δ|>ΔT. Since P(Δ) is not an even function, the ratio
![]()
is expected to be larger than unity for any value of σ and for any ΔT.
![[Fig. 1]](https://www.iucr.org/__data/assets/image/0003/8859/fig1.gif)
Figure 1 P(Δ) distribution for select values of σ
In Fig.2 we show RPM curves for different values of σ. RPM increases with σ and, for a given σ, increases with ΔT. Its value is strictly correlated with the ratio kd /kp : errors in the estimate of this ratio will produce anomalous values of RPM. For example, if Fd values are scaled so that they are larger than their true values, the number of positive Δ's will exceed the expected value. In the converse case the number of negative Δ's will be larger than the expected value. In practice, the experimental P(Δ) curve is modeled by different sources of errors: besides the scaling error, also icorrect estimates of the difference Bd -Bp (as a consequence of the scaling error, errors in measurements, lack of isomorphism, etc.) will generate anomalies in P(Δ).
The above considerations suggest that histogram-matching techniques can be usefully applied to transform the experimental Δ curve into the P(Δ) distribution expected at the chosen σ value. The resulting Δ values will then be introduced into (1) for obtaining more accurate triplet invariant estimates.
3.2 Phasing step
From (1) a weighted tangent formula may be derived![]()
![]() , (6)
, (6)
where j is defined by the equation [20]
![]()
and
![]()
The reliability parameter h of any determined phase h is modified according to the agreement between the calculated and the expected value of h. In particular, if h is larger than the expected value
![]() ,
,
then the calculated h is replaced by
![]() ,
,
where
![]() .
.
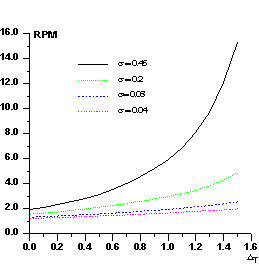
Figure 2 RPM curves for some representative values of against the threshold ΔT.
The weighting scheme is designed to drive phases towards values that mimize the difference between α and ![]() by reducing in the tangent refinement the importance of the phases with too large values of α.
by reducing in the tangent refinement the importance of the phases with too large values of α.
In one possible strategy for the phase determination one could simultaneously apply the tangent formula (6) to all the reflections up to derivative resolution. Such a strategy would require the calculation of several tens of millions of triplets, their cumbersome management by the tangent formula and large storage and computing time.
We have chosen a different strategy: first we phase a small set of reflections with large ![]() and R values ( i.e., batch 1, with NLAR reflections). The strategy is a multisolution one: a starting set of phases are generated by a random process [21]. Random phases are given to NLAR/2 reflections [22] with unit weights for the origin and enantiomorph-fixing reflections, and with weights equal to 0.8 for the others. Cycles of weighted tangent refinement are first applied to the NLAR/2 reflections and, after convergence, the phasing process is extended to all the NLAR reflections.
and R values ( i.e., batch 1, with NLAR reflections). The strategy is a multisolution one: a starting set of phases are generated by a random process [21]. Random phases are given to NLAR/2 reflections [22] with unit weights for the origin and enantiomorph-fixing reflections, and with weights equal to 0.8 for the others. Cycles of weighted tangent refinement are first applied to the NLAR/2 reflections and, after convergence, the phasing process is extended to all the NLAR reflections.
Among the various trials provided by the multisolution approach, the most probable one (on the basis of the figures of merit: see below) is used as a seed for phasing the remaining reflections. Batches of about 200 reflections, chosen in decreasing order of ||, are progressively phased via a phase extension procedure from batch number one.
3.3 The last step: picking up the correct solution
Figures of merit (FOMs) used in our procedure for picking the correct solution from the trial solutions are based on the theory described in two recent papers [23], [24]. Substantial modifications are, however, necessary to face the large complexity of the problem and to take advantage of the information contained in derivative data.The first FOM is ![]() , where
, where
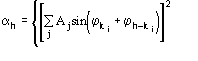
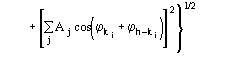
and
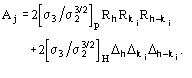
MABS gives a measure of the consistency of the triplet estimates, but it is not used as an active FOM for picking (in combination with others) the correct solution.
The second FOM (i.e., ALFCOMB) depends on the ratio ![]() , where
, where ![]() is given in [[section]]3.2. This expression for the variance holds in the absence of errors in measurements and in their mathematical treatment as well as in the presence of perfect isomorphism between native and derivative structures. If this is not the case, as with real data, the variance cannot be perfectly calculated and is probably underestimated by
is given in [[section]]3.2. This expression for the variance holds in the absence of errors in measurements and in their mathematical treatment as well as in the presence of perfect isomorphism between native and derivative structures. If this is not the case, as with real data, the variance cannot be perfectly calculated and is probably underestimated by ![]() . Accordingly, we used
. Accordingly, we used ![]() instead of
instead of ![]() in ALFCOMB.
in ALFCOMB.
The third FOM (PSICOMB) relies on the expectation that the distribution of the psi-zero triplets should be as random as possible. PSICOMB depends on the ratios ![]() , where
, where
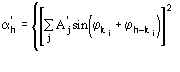
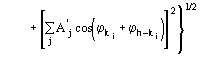
![]()
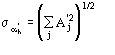 .
.
The weak reflections that constitute psi-zero triplets with the NLAR reflections are characterized by small values of both R and ![]() . Here, there is no room for a FOM based on classical negative quartet estimates based on native data only, which is unreliable for macromolecular structures of usual size.
. Here, there is no room for a FOM based on classical negative quartet estimates based on native data only, which is unreliable for macromolecular structures of usual size.
In our procedure negative and positive triplets play a similar role: they are nearly equal in number and reliability, and are both actively used in the phasing process. We decided to use the ratio ![]() as a FOM (CPHASE) involving both positive and negative estimated triplet phases
as a FOM (CPHASE) involving both positive and negative estimated triplet phases ![]() .
.
A combined figure of merit (CFOM) integrates the indications arising from ALFCOMB, PSICOMB and CPHASE. The combination of the various FOMs involves suitable weights which indicate our confidence in them. CFOM allows a satisfactory discrimination of correct versus wrong solutions (see Table 2 for some results). For all the test structures the highest CFOM solutions are the correct ones: in the Table 2 they are marked by bold characters. We note: i) figures in Table 2 refer to batch 1, as explained in [[section]]3.2. ii) in the last column the average phase error (ERR) is shown. It is sufficiently small for all the test structures but NOX. iii) The solution is found in few trials. For all the test structures the maximum number of trials we explored was 100. We don't claim that correct solutions always correspond to the highest CFOM values. Severe lack of isomorphism, errors in measurements and/or in the treatment of the experimental data will reduce the efficiency of the procedure.
Table 2 FOM values for the `best' trial solutions as ranked by CFOM for the various test structures
APP
Trial MABS ALFCOMB PSICOMB CPHASE CFOM ERR
14 1.10 0.23 0.54 0.91 0.49 30
28 1.10 0.23 0.53 0.91 0.49 30
7 1.10 0.22 0.47 0.91 0.47 82
29 1.09 0.20 0.46 0.91 0.46 83
24 0.75 0.00 0.68 0.68 0.43 84
BPO
18 0.84 0.40 0.96 0.75 0.63 29
6 0.58 0.15 0.80 0.57 0.48 84
19 0.58 0.14 0.79 0.57 0.48 83
E2
24 1.14 0.75 1.0 0.89 0.76 27
1 1.14 0.75 1.0 0.89 0.76 27
22 1.14 0.75 1.0 0.89 0.76 27
9 2.05 1.0 0.67 1.0 0.74 86
16 2.05 1.0 0.66 1.0 0.73 86
31 0.56 0.14 0.76 0.53 0.46 78
M-FABP
24 0.85 0.10 0.57 0.77 0.44 39
12 0.72 0.02 0.55 0.69 0.39 63
6 0.64 0.01 0.54 0.64 0.38 83
NOX
61 0.75 0.01 0.78 0.64 0.45 52
65 0.75 0.01 0.78 0.64 0.44 52
93 0.75 0.01 0.74 0.64 0.43 53
66 0.65 0.00 0.74 0.58 0.42 63
The solution may then not be recognizable by the figures of merit, and may be characterized by a high value of ERR. In extremely unfavourable cases the correct solution could not be obttained at all.
When the solution is not clearly recognizable, a further check can be used:
a) Difference Fourier synthesis with coefficients ![]() are calculated for the solutions with the highest values of CFOM. The maxima of the map should provide heavy-atom positions.
are calculated for the solutions with the highest values of CFOM. The maxima of the map should provide heavy-atom positions.
b) Such parameters are refined according to the phase refinement process [25].
c) If the refined positional parameters coincide with an allowed origin of the protein space group, then the trial solution is discarded from the set of reliable ones.
Steps a), b) and c) are executed in sequence without user intervention.
Why should such a process work? Readers accustomed to direct phasing of small molecules know that in symmorphic space groups the so-called `uranium solution' occurs quite frequently. It is marked by a high consistency of triplets phases, which are all close to zero. An observed Fourier synthesis would produce a huge maximum at an allowed origin. This type of false solution may be recognized and therefore discarded by special FOMs like the psi-zero and negative-quartet criteria. Since the psi-zero FOM described in paper II is not highly discriminating for macromolecules and the negative-quartet criterion is not among the used FOMs, the calculation of the difference Fourier synthesis for proteins is an efficient substitute for the specific FOMs. It is worthwhile emphasizing that a difference Fourier synthesis should not provide huge maxima at the allowed origins as for small molecules: since our phasing procedure uses a nearly equivalent number of positive and negative triplets, peak intensities in the maps corresponding to the `uranium solutions' are similar to peak intensities corresponding to true heavy-atom positions.
In Table 3, we show, for each test structure and for trial solutions highly ranked by CFOM, but corresponding to true or "uranium" solutions, the heavy-atom positions as obtained after some cycles of Fourier-least-squares calculations. Trials 7 and 29 for APP, 9 and 16 for E2, show maxima at allowed origins and could therefore be discarded. This increases the discriminating power of CFOM. It may be concluded that in general, if use is made of the above considerations, the correct solution can be found with higher reliability among the different trials.
Table 3 Heavy-atom positions for each test structure and for trial solutions highly ranked by CFOM (compare with Table 2). The correct solutions are in bold characters.
Structure Trial Heavy-atom position
Name
APP 14 28 0.246 0.009 0.227
7 29 0.244 0.010 0.226
0.000 0.390 0.500
0.000 .0396 0.500
BPO 18 0.591 0.026 0.279
0.221 0.112 0.311
E2 24 1 0.203 0.070 0.214
22 9 0.203 0.069 0.213
16 0.203 0.070 0.215
0.000 0.000 0.500
0.000 0.000 0.500
M-FABP 24 0.609 0.441 0.742
NOX 61 65 0.393 0.242 0.524
93 0.393 0.242 0.524
0.893 0.242 0.225
4 Intermediate results
The application of the above procedure to experimental data (see paper VI) produces electron density maps which are competitive with those generated by traditional SIR techniques. The results can be described as follows: a) without any information on the heavy-atom positions, the phasing process is able to provide in favourable cases electron density maps which may be directly interpreted; b) the process is able to phase all the reflections up to derivative resolution and may be accomplished in a fully automatic way, thereby adding appeal to the method; c) poor isomorphism between the native and derivative hinder a complete success: the maps are then not straightforwardly interpretable but still show interesting correlation with the correct maps. In Figs. 3a and 4a we show some details of the electron density map for BPO and M-FABP respectively, as obtained at the end of the procedure described in section 3. The solvent regions cannot be correctly distinguished from the protein regions, and the maps are hardly interpretable at this stage. For the readers benefit, in Figs. 3b and 4b we show the corresponding details in the "true" (obtained from the published model) BPO and M-FABP maps respectively. In order to provide the reader a numerical index, in Table 4 we show the correlation CORR of the electron density maps calculated via direct methods with the correct maps mod corresponding to the refined model phases, all reflections up to native resolution included. CORR has been calculated according to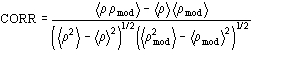
The highest CORR values are obtained for E2 and BPO, the derivatives of which are of extremely high quality. The worst phase values were obtained for NOX: the Pt derivative we used, as well as the other four derivatives of NOX, show serious lack of isomorphism [15].
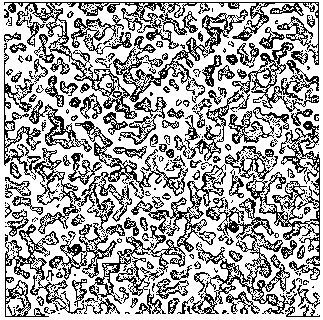
Figure 3a BPO- section y=0 of the map obtained by Direct Methods.

Figure 3b BPO- section y=0 of the true (obtained from the published model) map.

Figure 4a MFABP - section y=0 for the map obtained by Direct Methods.
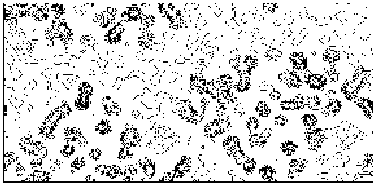
Figure 4b MFABP- section y=0 for the true (obtained from the published model) map.
Table 4 Mean phase error (ERR) for the test structure up to derivative resolution. NREF is the number of phased reflections up to derivative resolution. CORR is the correlation factor between direct methods map (derivative resolution) and "true" map (native resolution).
Structure NREF ERR(Weighted) CORR
Name
APP 1850 61 (57) 0.3927
BPO 12774 57 (52) 0.4490
E2 6575 57 (52) 0.5121
M-FABP 5456 64 (61) 0.3733
NOX 4066 73 (69) 0.3129
5 Phase refinement and extension up to native resolution
Refinement of the phases determined up to derivative resolution can be made as soon as a model of the heavy-atom structure is available. As specified in section 3 heavy-atoms are straightforwardly found by difference Fourier: their parameters (occupancy, coordinates and thermal factor) are then automatically refined.Several techniques for improving direct-method phases by incorporating the heavy-atom structure have been proposed: particularly notable are those proposed by Fortier, Moore & Fraser [26] and by Klop, Krabbendam & Kroon [27]. None of these methods were useful at this stage: the above techniques seem to work well when careful phase estimates are available, and at this stage this is not the case. However in a paper in preparation (Giacovazzo & Siliqi) it is shown that heavy-atom substructure can in favourable cases lead to a notable improvement of the phases determined as in section 4.
We show in Table 5 the mean-phase errors and the CORR values obtained when the heavy-atom substructure is available (to be compared with Table 4).
In terms of CORR only APP and M-FABP show remarkable improvement of the electron density map. In the other cases, the information of the heavy atom structure does not produce any improvement in term of CORR index, but reduces the heavy-atom residual in the electron density map. Accordingly, the new phases proved to be a better starting point for the application of techniques devoted to extending phases up to native resolution: we refer mostly to solvent flattening [28], [29] and histogram matching techniques [30], [31].
Table 5 Mean phase error (ERR) when the information on the heavy-atom structure has been exploited (data up to derivative resolution). NREF is the number of phased reflections up to derivative resolution. CORR is the correlation factor between direct methods map (derivative resolution) and "true" map (native resolution)
Structure NREF ERR(Weighted) CORR
Name
APP 1854 58 (53) 0.4667
BPO 12613 57 (48) 0.4525
E2 6408 56 (47) 0.5026
M-FABP 5616 64 (59) 0.3992
NOX 4006 74 (67) 0.2939
In the same paper by Giacovazzo & Siliqi, an innovate solvent-flattening procedure has been settled, which carefully extends and refines phases up to the native resolution. For our test structures, we show in Table 6 the final correlation values between our final electron density maps and the "true" maps. All the maps but NOX are easily interpretable, as is suggested by the high values of CORR. The serious lack of isomorphism of the Pt derivative of NOX did not allow the method to produce batch one phases sufficiently good to be used as a seed for subsequent expansion. NOX will be a useful test when two or more derivatives will be used by our direct methods procedure.
Table 6 Mean phase error (ERR) after the application of our solvent-flattening procedure: phase has been extended to the set of data up to native resolution. NREF is the number of phased reflections up to native resolution. CORR is the correlation factor between our final map and the "true" map.
Structure NREF ERR(Weighted) CORR
Name
APP 17058 51 (44) 0.8150
BPO 23956 52 (46) 0.7391
E2 10391 41 (38) 0.8761
M-FABP 7589 53 (46) 0.7093
NOX 4619 77 (74) 0.2743
To allow the reader to check the quality of the new maps we show: a) in Figs. 5a and 5b the APP skeleton obtained
from our map and from the "true" map respectively; b) In Figs. 6, 7a and 8 some sections of our electron density maps for BPO, E2 and M-FABP (to be compared with true electron density map sections shown in Figs. 3b, 7b and 4b respectively).
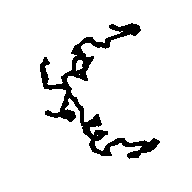
Figure 5a APP skeleton from our map (visualized by RasMol v2.3 by Roger Sayle)
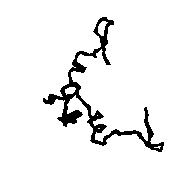
Figure 5b APP skeleton for the "true" map (visualized by RasMol v2.3 by Roger Sayle)
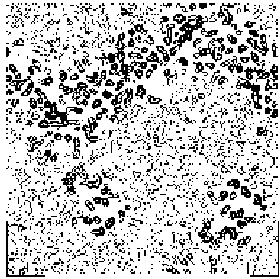
Figure 6 BPO section y=0 for the map obtained by applying our solvent flattening procedure to our Direct Methods map

Figure 7a E2 section y=0.3 for the map obtained by applying our solvent flattening procedure to our Direct Methods map.
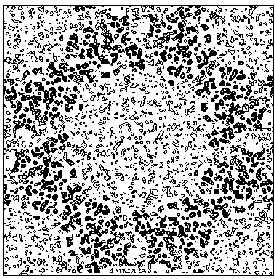
Figure 7b E2 section y=0.3 of the true (obtained from the published model) map.

Figure 8 M-FABP section y=0 for the map obtained by applying our solvent flattening procedure to our Direct Methods map
6 The representation theory and its integration with isomorphous replacement techniques
We have seen in section 3 that the availability of isomorphous derivative data reduces the complexity of the problem: triplet relations, which in the absence of derivative data are of orderorder ![]() . Since
. Since ![]() the triplet reliability increases, and the protein structure becomes solvable by direct methods. The above complexity reduction suggests that paraphernalia used with great success to solve small molecules could be resuscitated for application to macromolecules. A special wide-use and efficient tool is the theory of representations by Giacovazzo [32], [33] (see also Hauptman [34] for a related principle). The problem may be so stated: can we, for any phase invariant , arrange the (R, S) space in a sequence of subsets, each contained within the succeeding one and having the property that may be estimated, in order of expected effectiveness, from the (R, S) magnitudes constituting the subset? A solution to this question for SIR and OAS methods has been provided by Giacovazzo [35]. For the quartet invariant
the triplet reliability increases, and the protein structure becomes solvable by direct methods. The above complexity reduction suggests that paraphernalia used with great success to solve small molecules could be resuscitated for application to macromolecules. A special wide-use and efficient tool is the theory of representations by Giacovazzo [32], [33] (see also Hauptman [34] for a related principle). The problem may be so stated: can we, for any phase invariant , arrange the (R, S) space in a sequence of subsets, each contained within the succeeding one and having the property that may be estimated, in order of expected effectiveness, from the (R, S) magnitudes constituting the subset? A solution to this question for SIR and OAS methods has been provided by Giacovazzo [35]. For the quartet invariant
![]()
![]()
the first subset of magnitudes to exploit for the SIR case is
![]() . (7)
. (7)
For the triplet invariant the second representation will involve the subset
![]()
![]()
![]() (8)
(8)
where k is a free vector.
Such a procedure exploits for (8) the special quintets
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
....................
etc., where the quintets are obtained by permutation of and .
The calculation of the joint probability distribution function
![]()
![]() (9)
(9)
for quartets, and the derivation of the distribution
![]()
![]() (10)
(10)
for triplets, are quite complicated. However a technique has been recently settled [36], [37], [38] which allows such calculations.
6.1 The quartet invariant estimate
The joint probability distribution function (9) has been derived [36], [37] (see also [39] for a related method) via the Gram-Charlier expansion of the characteristic function. Let us denote![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
The conclusive conditional formula is
![]()
![]() (11)
(11)
where
![]()
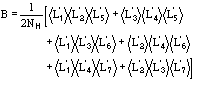
![]()
(12)
The main features of the formula may be so described:
a) the relation is of the order ![]() . Since
. Since ![]() is usually small, quartets are expected to be reliable (at least in principle).
is usually small, quartets are expected to be reliable (at least in principle).
b) the sign of A4 is determined by the product of two factors: the first is ![]() , which may be positive or negative, the second is the term
, which may be positive or negative, the second is the term ![]() which again may be positive or negative.
which again may be positive or negative.
c) 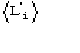 is the expected value of
is the expected value of ![]() In absence of prior information on the heavy-atom structure
In absence of prior information on the heavy-atom structure ![]() may only be estimated by probabilistic considerations [that is, by the formula (12)]. Errors in measurements, lack of isomorphism, etc., can make
may only be estimated by probabilistic considerations [that is, by the formula (12)]. Errors in measurements, lack of isomorphism, etc., can make ![]() remarkably different from
remarkably different from ![]() . In these cases quartet estimates are expected to be wrong. Once the heavy-atom structure becomes available, A4 may be replaced by
. In these cases quartet estimates are expected to be wrong. Once the heavy-atom structure becomes available, A4 may be replaced by
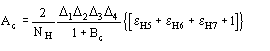 (13)
(13)
where
![]() Then quartet reliability proved to be comparable with triplet reliability. We show in Table 7 for some test structures the statistical calculations for assessing the reliability of the quartets having negative values of
Then quartet reliability proved to be comparable with triplet reliability. We show in Table 7 for some test structures the statistical calculations for assessing the reliability of the quartets having negative values of ![]()
Table 7 Statistical calculations for small-cross quartets by (13) (observed data).
APP E2 M-FABP
NR % |4|0 NR % |4|0 NR % |4|0
3621 71.6 114 10079 65.6 108 10084 54.9 96
1577 75.7 119 2224 74.8 118 1993 57.7 95
181 86.7 131 78 87.2 127 268 54.5 93
5 80.0 142 47 63.8 89
13 69.2 85
Table 8 BPO: statistical calculations for triplet invariants (found among the 1500 reflections with the largest of ||) relative to the formulas (2) and (15). Observed data for native and derivative structures are used.
(2) Positive estimated (15) Positive (15) Negative
triplets estimated triplets estimated triplets
ARG NR % ||0 NR % ||0 NR % ||0
0.2 25195 68 69 20107 72 65 2785 52 92
1.2 8680 72 64 10145 77 59 676 58 100
3.2 0 - - 531 84 50 30 40 98
4.4 0 - - 70 90 44 2 50 116
(2) Negative estimated (15) Positive (15) Negative
triplets estimated triplets estimated triplets
ARG NR % ||0 NR % ||0 NR % ||0
0.2 24805 68 110 2739 51 89 19688 71 115
1.2 6919 72 115 581 58 82 9485 76 120
3.2 0 - - 27 74 61 437 80 126
4.4 0 - - 8 75 67 45 78 122
Table 9 E2: statistical calculations for triplet invariants (found among the 855 reflections with the largest of ||) relative to the formulas (2) and (15). Observed data for native and derivative structures are used.
(2) Positive estimated (15) Positive (15) Negative
triplets estimated triplets estimated triplets
ARG NR % ||0 NR % ||0 NR % ||0
0.2 25058 72 65 19537 79 57 2967 62 104
1.2 4281 81 54 8088 85 50 599 74 119
3.2 0 - - 239 95 36 21 91 146
4.4 0 - - 30 100 23 1 100 159
(2) Negative estimated (15) Positive (15) Negative
triplets estimated triplets estimated triplets
ARG NR % ||0 NR % ||0 NR % ||0
0.2 24942 71 114 2961 64 74 19234 78 122
1.2 3234 81 126 531 75 62 7161 85 131
3.2 0 - - 27 85 56 207 94 143
4.4 0 - - 7 86 55 17 100 157
6.2 The triplet invariant estimate via its second representation
The joint probability distribution (9) has been derived [38] via the Gram-Charlier expansion of the characteristic function. Let us denote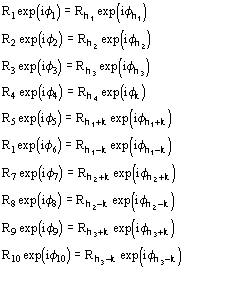
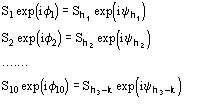
The conclusive formula estimating the triplet invariant may be written as
![]() (14)
(14)
where
![]()
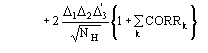 (15)
(15)
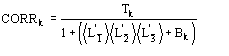
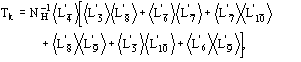
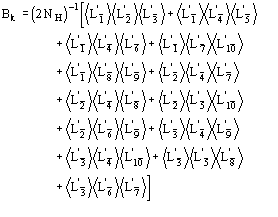 We observe:
We observe:
a) the distribution (14) is a von Mises-type function: it is unimodal, and the expected value of is 0 or according to whether A is positive or negative.
b) for proteins the term ![]() is quite often negligible with respect to the second term in (15). It can be neglected.
is quite often negligible with respect to the second term in (15). It can be neglected.
c) the contribution from the second phasing shell can change the value of the expected phase. According to the first representation formula, is expected to be zero if ![]() is positive, is expected to be if
is positive, is expected to be if ![]() is negative. In the second representation formula the term
is negative. In the second representation formula the term ![]() may be considered a correction term which modulates the first representation estimate. If
may be considered a correction term which modulates the first representation estimate. If ![]() the second representation estimate is different by from the first representation estimate.
the second representation estimate is different by from the first representation estimate.
As in the quartet case ![]() is an estimate of
is an estimate of ![]() , which may fail when lack of isomorphism and/or errors in the experimental data occur. If the heavy-atom structure is available then
, which may fail when lack of isomorphism and/or errors in the experimental data occur. If the heavy-atom structure is available then ![]() may be used instead of
may be used instead of ![]() . We show in Tables 8 and 9 the applications of (15) to E2 and BPO experimental data. The data should be read as follows: triplet estimated positive by (2) are split by (15) in positive and negative estimated triplets. Analogously, triplets estimated negative by (2) are splitted by (15) in positive and negative subsets. It is evident that (15) is more efficient than (2) in ranking triplet reliability and in estimating their cosine sign. A useful practical detail is that the results in Tables 8 and 9 are obtained by exploiting only (about) 20 quintets per triplet.
. We show in Tables 8 and 9 the applications of (15) to E2 and BPO experimental data. The data should be read as follows: triplet estimated positive by (2) are split by (15) in positive and negative estimated triplets. Analogously, triplets estimated negative by (2) are splitted by (15) in positive and negative subsets. It is evident that (15) is more efficient than (2) in ranking triplet reliability and in estimating their cosine sign. A useful practical detail is that the results in Tables 8 and 9 are obtained by exploiting only (about) 20 quintets per triplet.
7 The partial structure as a source of prior information
A probabilistic formula by Giacovazzo [9] originally designed for small molecules, allows the recover of the complete from a partial structure. The formula may be written as![]()
![]() (16)
(16)
If the known partial structure is negligible (in terms of number of electrons) with respect to the complete structure then
![]()
and (16) reduces to Sayre's equation.
In terms of phases (16) is equivalent to
![]()
(17)
where
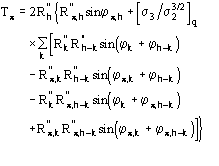
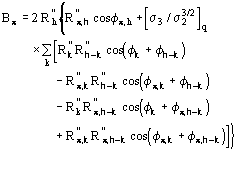
![]() is the most probable value of
is the most probable value of ![]() and
and
![]() (18)
(18)
is its reliability parameter.
Equation (16) has been recently reconsidered with respect to its possible use in macromolecular crystallography. In a feasibility study by Giacovazzo & Gonzalez-Platas [10], experimental tests on protein data show that the formula is potentially able to estimate phases accurately, provided 30-40% of the electron density is correctly located. Real cases were not examined. In the future, eq. (16) will be applied to a situation frequently occurring in practice: phase extension from derivative to native resolution, and phase refinement. The use of (16) is the reciprocal counterpart of electron density modification techniques. Indeed a basic step of these techniques is to fix criteria to define the structure part, say  ; by Fourier inversion is calculated. Once this has been made is used, in combination with the old values, as better approximation of the true phase value.
; by Fourier inversion is calculated. Once this has been made is used, in combination with the old values, as better approximation of the true phase value.
On the other hand (16) comes from the electron density squaring under the prior condition that ![]() is known. The supplemental contribution of order
is known. The supplemental contribution of order ![]() comes from the squaring of the unknown part of the structure under the restraint that
comes from the squaring of the unknown part of the structure under the restraint that ![]() is known. To devise the optimal use of (9) for practical cases is not straightforward, because it involves good approximations of the phases
is known. To devise the optimal use of (9) for practical cases is not straightforward, because it involves good approximations of the phases ![]() and
and ![]() (which are not always available). Presently we are exploring different approaches.
(which are not always available). Presently we are exploring different approaches.
8 Molecular replacement techniques and direct methods
The role of direct methods in the molecular replacement area has so far been quite marginal. Main [40] considered, among other kinds of prior information, the following ones: a) randomly positioned and randomly oriented atomic groups; b) randomly positioned but correctly oriented atomic groups. Such categories of information give rise to a von Mises distribution for triplet invariant phases such as![]() (19)
(19)
where Q and ![]() can be defined in terms of the prior information, and the E's are the structure factors normalized by taking the prior into account.
can be defined in terms of the prior information, and the E's are the structure factors normalized by taking the prior into account.
In case a) the Main formula encompasses a previous Hauptman [41] formula [called B(z,t)] which is devoted to calculating the average of an exponential term which goes over all orientations of the triangle formed by three atoms:
![]() In case b),
In case b), ![]() is expected to lie between 0 and 2: the use of such values and of the corresponding reliability parameter should automatically translate the model structure in the correct position.
is expected to lie between 0 and 2: the use of such values and of the corresponding reliability parameter should automatically translate the model structure in the correct position.
Additional phase relationships (which are not structure invariants or seminvariants) devoted to the translation problem were obtained by Giacovazzo [42] for polar space groups. In such cases the shift which brings a molecular fragment from a trial to the correct position may be restricted to a region which is smaller than the unit cell. For example, in P21 the origin may be freely chosen along the diad axis, and therefore may be restricted to the family of vectors [x 0 z]. This restriction is transformed, in the probabilistic approach, into supplemental prior information, so that one-phase, two-phase, three-phase relationships can be found (none of them being a structure invariant) which can be used for translating a molecule in the correct position. The Main formula (at least to the knowledge of the authors) has never been applied to proteins, or rotating nor for translating a molecule from a trial position. Giacovazzo's formulas were never applied to practical cases. In a forthcoming paper [43] it is shown that direct procedures can be successfully applied to macromolecules for translation purposes. We shortly quote here one of the experimental tests. M-FABP was originally solved by using multiple isomorphous replacement and molecular replacement procedures [14]. The model of adipocyte lipid binding protein (A-LBP), obtained from 2.5 resolution, was used as a search model from molecular replacement. The rotation function in MERLOT [44] was used to orient the molecule and a translation search was made by XPLOR [45] using 1351 reflections between 15 and 2.5 resolution. The same rotation procedure was followed in the paper by Giacovazzo, Manna & Siliqi, but the translation search was performed by direct methods. The solution with the highest CFOM corresponds to the correct translation. Our solvent-flattening procedure mentioned in section 5, automatically applied to direct-method phases, produced an electron density map having a correlation factor of 0.6 with the "true" map. In Fig. 9 we show the section at y=0.0 of the resulting electron density map, which may be usefully compared with the "true" section in Fig. 4b.

Figure 9 M-FABP section y=0 of the map obtained by translating via Direct Methods the model molecule, and subsequently, by applying our solvent-flattening procedure.
9 Conclusions
This paper shows that direct methods can be successfully applied to many of the problems encountered in macromolecular crystallography. Indeed:a) they are competitive with traditional isomorphous derivative techniques, with the supplemental appeal due to their high degree of automation;
b) they can profit from anomalous dispersion effects;
c) they can be applied to translating a molecule from a trial to the correct position.
Only for point a), and particularly for the SIR case, has a well established direct procedure been described. The MIR case however will easily follow. Point b) is still at an earlier stage even if notable results have been obtained from various authors. Point c) is starting. The rotation problem, so basic for the molecular replacement area, has not been attempted for macromolecules by direct methods. We intend to show that even in this area direct methods can offer an important contribution.
The authors are grateful to Drs H.J. Hecht, W. Hol, A. Mattevi and G. Zanotti for having provided protein diffraction data and for useful discussions.
References
[1] Hauptman, H. (1982). Acta Cryst. A38, 289-294.[2] Giacovazzo, C., Siliqi, D. & Ralph, A. (1994). Acta Cryst. A50, 503-510.
[3] Giacovazzo, C., Siliqi, D. & Spagna, R. (1994). Acta Cryst. A50, 609-621.
[4] Giacovazzo, C., Siliqi, D. & Zanotti, G. (1995). Acta Cryst. A51, 177-188.
[5] Giacovazzo, C., Siliqi, D. & Gonzalez-Platas, J. (1995). Acta Cryst. A51, 811-820.
[6] Giacovazzo, C., Siliqi, D., Gonzalez-Platas, J. Hecht, H., Zanotti, G. & York, B. (1995). Acta Cryst. D52, 813-825.
[7] Hauptman, H. (1982). Acta Cryst. A38, 632-641.
[8] Giacovazzo, C. (1983). Acta Cryst. A39, 585-592.
[9] Giacovazzo, C. (1983). Acta Cryst. A39, 685-692.
[10] Giacovazzo, C. & Gonzalez-Platas, J. (1995). Acta Cryst. A51, 398-404.
[11] Glover, I., Haneef, I., Pitts, J., Woods, S., Moss, D., Tickle, I. & Blundell, T. L. (1983). Biopolymers, 22, 293-304.
[12] Hecht, H., Sobek, H., Haag, T., Pfeifer, O. & Van Pee, K. H. (1994). Nature Struct. Biol. 1, 532-537.
[13] Mattevi, A., Obmolova, G., Schulze, E., Kalk, K. H., Westphal, A. H., De Kok, A. & Hol, W. G. J. (1992). Science, 255, 1544-1550.
[14] Zanotti, G., Scapin, G., Spadon, P., Veerkamp, J. H. & Sacchettini, J. C. (1992). J. Biol. Chem. 267, 18541-18550.
[15] Hecht, H., Erdmann, H., Park, H., Sprinzl, M., Schmid, R. D. & Schomburg, D. (1993). Acta Cryst. A49, Suppl. 86.
[16] Hauptman, H., Potter, S. & Weeks, C. M. (1982). Acta Cryst. A38, 294-300
[17] Fortier, S., Weeks, C. M., Hauptman, H. (1984). Acta Cryst. A40, 544-548
[18] Giacovazzo, C., Cascarano, G. & Zheng, C.-D. (1988). Acta Cryst. A44, 45-51.
[19] Blundell, T.L. & Johnson, L.N. (1976). Protein Crystallography, p. 336, London: Academic Press.
[20] Altomare, A., Cascarano, C., Giacovazzo, C., Guagliardi, A., Burla, M.C., Polidori, G. & Camalli, M. (1994). J. Appl. Cryst. 27, 435.
[21] Baggio, R., Woolfson, M.M., Declercq, J-P. & Germain, G. (1978). Acta Cryst. A34, 883-892
[22] Burla, M.C., Cascarano, G. & Giacovazzo, C. (1992). Acta Cryst. A48, 906-912.
[23] Cascarano, G., Giacovazzo, C. & Viterbo, D. (1987). Acta Cryst. A4843, 22-29.
[24] Cascarano, G., Giacovazzo, C. & Guagliardi, A. (1992b). Acta Cryst. A48, 859-865.
[25] Dickerson, R.E., Kendrew, J.C & Strandberg, B.E. (1961). Acta Cryst. 14, 1188-1195.
[26] Fortier, S., Moore, N. J. & Fraser, M. E. (1985). Acta Cryst. A41, 571-577.
[27] Klop, E. A., Krabbendam, H. & Kroon, J. (1987). Acta Cryst. A43, 810-820.
[28] Wang, B.C. (1985). In "Methods in Enzymology", Vol.115 (Wyckoff, H.W., Hirs, C.H.W. and Timasheff, S.N., ed.), p.90-112.
[29] Leslie, A.G.W (1987). Acta Cryst. A43, 41-46
[30] Lunin, V. Y (1993). Acta Cryst. D49, 90-99.
[31] Zhang, K.Y.J. & Main, P. (1990). Acta Cryst. A46, 41-46
[32] Giacovazzo, C. (1977) Acta Cryst. A33, 934-944
[33] Giacovazzo, C. (1980) Acta Cryst. A36, 362-373
[34] Hauptman, H. (1976). Acta Cryst. A32, 934-940
[35] Giacovazzo, C. (1984) International School of Crystallography, lecture notes, in Direct Methods of Solving Crystal Structures, Erice, Italy
[36] Giacovazzo, C. & Siliqi, D. (1996). Acta Cryst. A52, 133-142
[37] Giacovazzo, C. & Siliqi, D. (1996). Acta Cryst. A52, 143-151
[38] Giacovazzo, C. & Siliqi, D. (1996). Acta Cryst. A53, 000-000 (submitted)
[39] Kiriakidis, C.E., Peschar, R. & Shenk, H. (1996) Acta Cryst. A52, 77-87
[40] Main, P. (1976) Crystallographic Computing Techniques, edited by F. Ahmed, p 99-105, Copenhagen; Munskgaard
[41] Hauptman, H. (1965). Z. Krist. 121, 1-8
[42] Giacovazzo, C. (1988). Acta Cryst. A44, 294-300.
[43] Giacovazzo, C., Manna, L. & Siliqi, D. (1997) in preparation
[44] Fitzgerald, P.M.D. (1988). J. Appl. Cryst. 21, 273-278.
[45] Brunger, A.T. (1990) XPLOR version 2.1, manual. A system for crystallography and NMR.
These pages are maintained by the Commission Last updated: 15 Oct 2021


![[Commission Home Page] [Commission logo]](https://www.iucr.org/__data/assets/image/0008/149381/cc_textlogo.png)