It was pointed out by Hamilton (1959) and by Willis & Pryor (1975) that for minor departures from isotropic motion, or for anisotropic displacement parameters deemed to be physically insignificant, it may be worthwhile to replace the six-parameter description of anisotropic motion by a single quantity, which should describe an isotropic equivalent to the weakly or dubiously anisotropic case.
The IUCr Commission on Journals (1986) recommended that ``equivalent isotropic displacement parameters" be computed from the expressions proposed by Hamilton (1959) and by Willis & Pryor (1975). However, a number of different incorrect expressions have also been used (Fischer & Tillmanns, 1988), and this has led to considerable confusion. We first review the proper definitions and demonstrate their equivalence.
The first definition of the equivalent isotropic displacement parameter, as given by Hamilton (1959) and Willis & Pryor (1975), is
with 
an element of a mean-square displacement tensor, referred
to a Cartesian basis [see eqs. (2.1.34) - (2.1.37)].
The trace of 
, as given on the right-hand side
of eq. (2.2.51), is equivalent to the sum of the eigenvalues of this
matrix. These eigenvalues are often computed,
since an eigenvalue of the matrix represents the
mean-square displacement along the corresponding eigenvector.
The right-hand side of eq. (2.2.51) can then be interpreted as a
mean-square displacement averaged over all directions.
Equation (2.2.51) can thus be applied to the computation of 
either by taking the trace of , which was obtained from
eq. (2.1.44) or eq. (2.1.49), or by using the sum of the
eigenvalues of . However, it is essential to note that
eq. (2.2.51) holds only for the Cartesian displacement tensor
. It will give incorrect values of if U
is referred to oblique basis vectors and its trace taken instead of
that of .
Since the basis vectors of the Cartesian system have the property
, a consideration of eqs.
(2.1.35), (2.1.37), and (2.2.51) readily leads to
This equation is a convenient starting point for testing the equivalence of
various definitions of . The second definition by Willis
& Pryor (1975) is the first line of the next equation
with g the real space metric tensor. This shows that eqs.
(2.2.51) and (2.2.53), the two recommended definitions of
, are equivalent.
If we make use of eqs. (2.2.54) and (2.1.38), two additional
expressions for can be obtained:
and
Thus, eqs. (2.2.51), (2.2.54), (2.2.55), and
(2.2.56) are equivalent representations of the equivalent isotropic
mean-square displacement parameter , obtainable from the commonly
employed anisotropic displacement parameters.
We can also arrive at eq. (2.2.54) by directly combining eqs. (2.1.44) and (2.2.51), and making use of a known property of the matrix A. We have
since
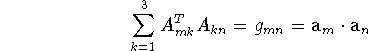
(e.g., Prince, 1982). This derivation shows that the value of
does not depend on the particular
form of the matrix A, which transforms the components of u from
the lattice to the Cartesian basis.
Acta Crystallographica requires that published values of
be accompanied by an evaluation of the standard deviation (now standard
uncertainty) in these quantities. The calculation of this estimate is
described in detail by Schomaker and Marsh (1983). A useful measure of
the anisotropy of the mean-square displacement tensor is the ratio of its
minimum and maximum eigenvalues. We recommend that published or
deposited values of be accompanied by both the standard
uncertainties and the ratio of the minimum to the maximum eigenvalues
of the corresponding anisotropic displacement tensors. Both the
uncertainty of and the ratio may be
helpful in judging the extent to which the use of is justified.
