4. The Use of Stereographic Nets

Stereographic projections of the highest accuracy are obtained by the constructions described in the previous section, and they have been described first because they lead to an understanding of the principles involved. However, it is often more convenient to prepare stereograms with the help of stereographic nets, and although the accuracy obtained is usually lower it is sufficient for most purposes.

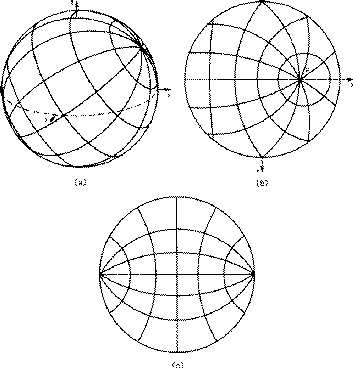
A stereographic net is simply a stereographic projection of the lines of latitude and longitude of a sphere on to a central plane. The most obvious form of stereographic net is shown in Fig. 12. The N-pole projects to the centre as discussed in Section 1, the lines of latitude project to a set of concentric circles, and the lines of longitude to a set of diameters of the primitive. Such a net, if graduated sufficiently finely, could be used directly to obtain the same results as constructions (i) and (iv) of Section 3. However, other nets are possible. If we imagine a terrestrial globe tilted over as shown in Fig. 13a, and we project all points on it, not to the geographical S-pole but to the lowest point of the sphere, then the projection of the lines of latitude and longitude would be as shown in Fig. 13b. We shall revert to this idea in Section 5, but the most generally useful result is if we tilt the globe right over so that its N-S axis is horizontal. The projection is then as shown in Fig. 13c. It is equivalent to what we would have obtained by projecting to its S-pole a globe that was inscribed with lines of latitude and longitude referred to as `east pole` and `west pole`. 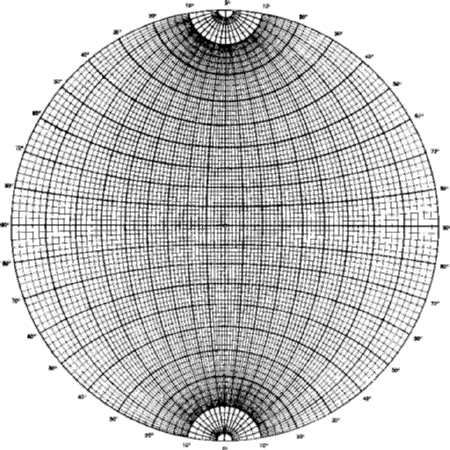This is the Wulff net , and is so generally useful that it is commonly referred to as the stereographic net. A commercially available Wulff net of 5 inch diameter graduated in 2 $^{\circ}$ intervals is shown in Fig. 14. On this figure all the (nearly) vertical lines represent great circles, and all the (nearly) horizontal lines represent small circles round a point on the primitive.

**Figure 12:** Stereographic projection of lines of latitude (90 $^{\circ}$ N to 30 $^{\circ}$ S) and longitude.
$\begin{figure} \includegraphics {fig12.ps} \end{figure}$

**Figure 13:** (a) Tilted sphere with lines of latitude and longitude. (b) Stereographic projection of (a) to its lowest point; the projection is therefore on the plane of the x and y axes indicated in (a). (c) Stereographic projection of the lines of latitude and longitude to the lowest point of a sphere that has been tilted right over so that its axis is horizontal (the Wulf net).
$\begin{figure} \includegraphics {fig13.ps} \end{figure}$

**Figure 14:** The 5 inch diameter Wulff net. Note that this net is rotated 90 $^{\circ}$ from the orientation of that shown in Fig. 13c.
$\begin{figure} \includegraphics {fig14.ps} \end{figure}$

In order to construct stereograms with the help of the Wulff net it is most convenient to work on tracing paper over the net.

To plot a point at a given angle from the N-pole (equivalent to construction (i)) one simply uses the scale along either of the graduated diameters of the net.

To draw a great circle through two points (equivalent to construction (iii)) rotate the stereogram over the net until both points lie on one of the projected great circles (or an interpolated circle between two of them) and then trace the required arc on to the stereogram. Because of the simplicity of this procedure one does not need construction (ii). If the two points have been projected to opposite poles (i.e. one is a $\times$ and the other a $\circ$ ) then rotate the stereogram until they lie on projected great circles at equal distances on opposite sides of the vertical diameter of the net.

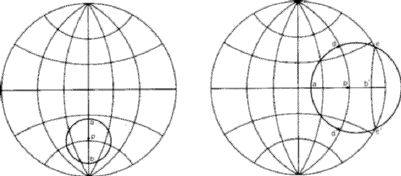
To draw a small circle of given radius $\theta$ about a point p (equivalent to construction (iv)) rotate the stereogram over the net so that the p point lies on the vertical diameter. If there are two points at the appropriate scale distances on opposite sides of p and within the primitive, then mark these two points and draw a circle through them centred at their mid point (Fig. 15a). If p is closer to the primitive than the required angular radius then only one of the required points (a) can be found on the net. The second point required (b) can most simply be found by using a stereographic ruler. This is a scale whose graduations are equal to those along a diameter of the Wulff net, but which continue appropriately to some (arbitrary) distance beyond the primitive.

**Figure 15:** Construction of the stereographic projection of a small circle round a point p, using the Wulff net: (a) when the projected circle is wholly within the primitive: (b) when it extends outside the primitive.
$\begin{figure} \includegraphics {fig15.ps} \end{figure}$

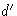However, if a stereographic ruler is not available the Wulff net itself can be used. Position the point p on the horizontal diameter of the net and mark two points d and $d^{\prime}$ (Fig. 15b) above and below p at distances $\theta$ along the (interpolated) great circle through p. Then the required small circle can be drawn through a, d and $d^{\prime}$ . Once the circle has been drawn it is possible to reproject to the N-pole the part that lies outside the primitive. 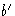Count divisions along the diameter from p to the primitive and then continue counting back inwards until the value of $\theta$ is reached: this leads to a point $b^{\prime}$ (Fig. 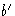15b) and the required arc is that which goes through $b^{\prime}$ and the two intersections e and $e^{\prime}$ of the small circle with the primitive.

If the point p lies on the primitive, then the stereogram must be rotated so that p lies at one end or the other of the vertical diameter of the Wulff net. A projected small circle of any desired angular radius can then be traced directly from the Wulff net.