2. Combination of Symmetry Elements in Finite Groups

The complete symmetry displayed by an isolated object or group of objects is its point group , there being always at least one point common to all the symmetry elements. We have already met such a collection of symmetry elements in Figs. 1.3c and 1.4c, comprising two mirror planes intersecting in a twofold axis. Note that no single one of these elements can be left out of the group, because the presence of any two creates the third. This being so, two of the elements are sufficient to define the whole, and this particular point group is normally given the short symbol mm , rather than the full symbol 2mm or mm2.

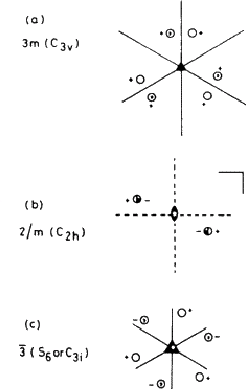
Similarly, three mirror planes meeting in a threefold axis (Fig. 2.1a) are adequately represented by 3m . The full symbol 3mmm is not needed because two of the `m 's are redundant, being created by the action of the threefold axis on the other one. Fig. 2.1b shows a mirror plane perpendicular to a twofold rotation axis; this is given the symbol 2/m , the `/' implying `perpendicular to`. (Note that the combination produces a centre of symmetry at the point where the rotation axis intersects the mirror plane.)

**Fig. 2.1.** Some combinations of symmetry elements with their point-group symbols. The equivalent *Schoenflies* symbol is given in brackets.
$\begin{figure} \includegraphics {fig2.1.ps} \end{figure}$

This system of nomenclature, which is the one most often used in crystallography is largely self-explanatory, and with very little practice one can draw the appropriate collection of symmetry elements and asymmetric units for any symbol. There is also an older system in use which is not so convenient for our purposes; in Fig. 2.1 examples of this Schoenflies notation are given in brackets after the crystallographic (Hermann-Mauguin ) notation: a concordance between the two is given in Table 1. A major difference is that the operator that we have called an inversion axis $\bar{n}$ (= n -fold rotation plus inversion through a point) is replaced by an alternating axis S _n (= rotation plus reflection across a plane) in the Schoenflies notation. Moreover, as Fig. 2.1c shows, n may change: a threefold inversion axis corresponds to a sixfold alternating axis. Inconvenient though this may be, it does illustrate that the distinction between three- and sixfold symmetry is sometimes a matter of definition, and therefore arbitrary.

There are thirty-two distinct combinations of the crystallographic symmetry operations that relate to finite groups, and thus there are thirty-two point groups or crystal classes ; crystals often reveal the class to which they belong through the symmetry of their external forms. These crystal classes are conveniently grouped into systems according to the restrictions placed on the shape of the unit cell (see next section) by the symmetry of its contents. This is summarised in Table 1.

**Table 1:** Crystal systems and classes (equivalent *Schoenflies* nomenclature for the latter in brackets)
System	Characteristic symmetry	Unit cell shape	Lattice types	Classes
Triclinic	None	$a\neq{}b \neq c$ *	P	$1(C_1),\bar{1}(C_i,S_2)$
		$\alpha \neq \beta \neq \gamma \neq 90^{\circ}$
Monoclinic	One twofold axis (2 or $\bar{2}\equiv m$ )	$a\neq{}b \neq c$	P,C (or A)	$2(C_2), m[=\bar 2](C_s)$
		$\alpha=\gamma=90\neq\beta$		2/m(C_2h)
Orthorhombic	Three mutually perpendicular twofold axes	$a\neq{}b \neq c$	P,C,	222(D₂), mm2(C_2v)
		$\alpha=\beta=\gamma \pm 90^{\circ}$	(or A orB)	mmm(D_2h)
			I,F
Tetragonal	One fourfold axis	$a=b\neq c$	P,I	$4(C_4), \bar4(S_4), 4/m(C_{4h}),$
		$\alpha=\beta=\gamma=90^{\circ}$		422(D₄), 4nn(C_4v)
				$\bar4 2m(D_{2d}), 4/mmm(D_{4h})$
Trigonal	One threefold axis	$a=b\neq c$	P<R	3(C₃), 3(S₆,C_3i), 32(D₃)
		$\alpha=\beta=90^{\circ}$	3m(C_3v), 3m(D_3d)
		$\gamma=120^{\circ}$
Hexagonal	One sixfold axis	$a=b\neq c$	P	$6(C_6), \bar6 (C_{3h}), 6/m(C_{6h})$
		$\alpha=\beta=90^{\circ}$		$622(D_6), 6mm(C_{6v}) \bar6 m2(D_{3h})$
		$\gamma=120^{\circ}$		$\bar6 /mmm(D_{6h})$
Cubic	Four threefold axes (along body diagonals of a cube)	a=b=c	P,I,F	23(T), m3(T_h), 432(O)
		$\alpha=\beta=\gamma=90^{\circ}$		43m(T_d), m3m(O_h)

* That is, no restrictions.