This is an archive copy of the IUCr web site dating from 2008. For current content please visit https://www.iucr.org.

The |E|'s of H and 2H: The $\sum_1$ Relationship

The $\sum_1$ relation is the first phase relationship which will be considered here; it estimates in centrosymmetric space groups the phase of reflection 2H on the basis of the magnitudes |E_H| and |E_2H|. To start with, geometrical considerations will be applied to reflections with simple indices.

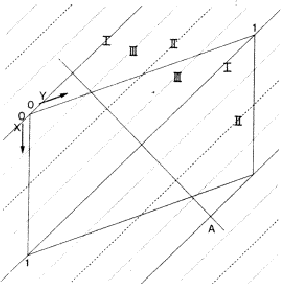
In a centrosymmetric crystal only phases of 0 and $\pi$ occur; provided that the phase of the 110 reflection is 0 the maxima of the associated electron density wave are found at the lines I of Fig. 2 and the minima at the lines II. If the phase of 110 is $\pi$, the maxima and minima are interchanged. The lines where the electron density wave has 0 value are marked with III. Thus in the event |E₁₁₀| is large and $\phi_{110}$ = 0, the electron density is mainly concentrated in the shaded areas of Fig. 3. For the electron density wave associated with the 220 reflection the maxima are found at both lines I and II in Fig. 2 in the case its phase is 0 and the minima at the lines III. Thus, when |E₂₂₀| is large and $\phi_{220}$= 0 the atoms must lie in shaded areas in Fig. 4. A similar drawing can be made for $\phi_{220}$ = $\pi$.

Figure 2: Lines of equal contribution to the electron density of the reflections hh0. E.g. for reflections 110 with $\phi_{110}$ = 0 the contribution to the electron density is maximum at lines I, minimum at lines II and zero at lines III.

Figure 3: In case |E₁₁₀| is large and $\phi_{110}$ = 0 the atoms are likely to be found in the shaded areas.

Figure 4: For |E₂₂₀| large and $\phi_{220}$ = 0 the electron density is more likely to be present in the vertically shaded areas.

The combination of the two electron density waves associated with the reflections 110 and 220 leads to Fig. 5, in which in the areas I maxima are found of both density waves. In the areas II the maximum of 220 coincides with the minimum of 110, resulting in a low density. In the event that both reflections have a large |E| value it is likely that the atoms are concentrated in the double shaded area.

In case the phase $\phi_{220}$ = $\pi$, the vertically shaded areas shift to the blank regions of Fig. 5 and then there is no overlap between the horizontally (110) and vertically (220) shaded areas; this implies that no position for the atoms can be found in which they contribute strongly to both structure factors. As a result for $\phi_{220}$ = $\pi$ and $\phi_{110}$ = 0 it is not likely that both structure factor magnitudes |E₁₁₀| and |E₂₂₀| are large.

Figure 5: Superposition of Figs. 3 and 4. In the areas I the shaded areas from the 110 and 220 reflections coincide. In case both reflections are large this is a rather likely situation.

In conclusion, for large structure factors |E₁₁₀| and |E₂₂₀|, it is likely that $\phi_{220}$ = 0; this relationship is known as the $\sum_1$relation.

Up to now no attention is paid to the situation $\phi_{110}$ = $\pi$, the reader is invited to show that this gives no change in the formulation of the $\sum_1$relation.

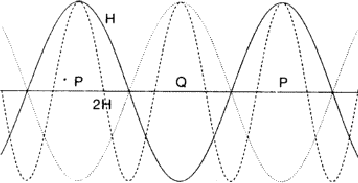
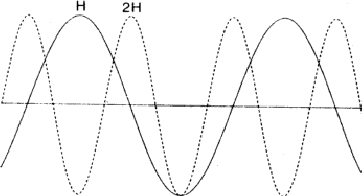
The comparison of H and 2H can be considered as a one-dimensional problem which can be understood by looking along line A in Fig. 2. In Fig. 6 the situation along this line is sketched with $\phi_H$ = $\phi_{2H}$ = 0 while in Fig. 7 $\phi_H$ = 0 and $\phi_{2H}$ = $\pi$. Areas labelled P in Fig. 6 denote regions of considerable positive overlap, whereas in Fig. 7 only regions of minor positive overlap are seen. The implication is that for large |E_H| and |E_2H| the situation depicted in Fig. 6 is more probably true and thus $\phi_{2H}$ = 0. When $\phi_H$ = $\pi$, as denoted by the dotted line in Fig. 6 the overlap areas marked Q show that $\phi_{2H}$ is still zero.

Figure 6: The drawn line H gives the electron density wave for $\phi_H$ = 0, and its dotted mirror image the wave for $\phi_H$ = $\pi$. The maximum of the dashed line 2H coincides with the maxima of the drawn line H in P and with the maxima of the dotted one in Q. Thus if |E_H| and |E_2H| are large, it is likely that $\phi_{2H}$ = 0 whatever the phase of H.

Figure 7: Here the unlikely situation is depicted that for strong reflections H and 2H $\phi_H$ = 0 and $\phi_{2H}$ = $\pi$. There is no positive overlap and therefore if |E_H| and |E_2H| are both large this situation is much more unlikely to exist than the situation of Fig. 7.

Copyright © 1984, 1998 International Union of Crystallography