Next: Large |EH|, |EK| and |E-H-K|: The Up: An Introduction to Direct Methods. The Previous: The |E|'s of H and 2H:
![[IUCr Home Page]](/iucr-top/logos/iucrhome.gif)
![[Commission Home Page]](/iucr-top/logos/cteach.gif)
![]()
![]()
![]()
Next: Large |EH|, |EK| and |E-H-K|: The
Up: An Introduction to Direct Methods. The
Previous: The |E|'s of H and 2H:
In 1948 Harker and Kasper published their paper on inequality relationships, which actually opened the field of direct methods. They applied the Cauchy inequality:
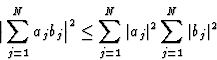 |
(8) |
| (9) |
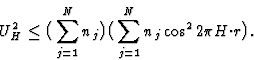 |
(10) |
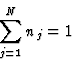 |
(11) |
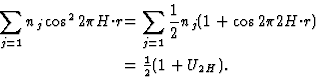 |
(12) |
| (13) |
In case ![]() then
then ![]() or in other words the sign
of reflection 2H is positive whatsoever its |U2H| value is. Note that
the sign of H may have both values. In practice
or in other words the sign
of reflection 2H is positive whatsoever its |U2H| value is. Note that
the sign of H may have both values. In practice ![]() does
not often occur. However, when |U2H| is large, expression (13) requires
the sign of 2H to be positive even if UH is somewhat smaller than
does
not often occur. However, when |U2H| is large, expression (13) requires
the sign of 2H to be positive even if UH is somewhat smaller than
![]() . Moreover, when |UH| and |U2H| are reasonably large, but
at the same time (13) is fulfilled for both signs of 2H, it is still more
likely that S2H = + than that S2H = -. For example, for |UH| = 0.4
and |U2H| = 0.3, S2H = + leads in (13) to 0.16
. Moreover, when |UH| and |U2H| are reasonably large, but
at the same time (13) is fulfilled for both signs of 2H, it is still more
likely that S2H = + than that S2H = -. For example, for |UH| = 0.4
and |U2H| = 0.3, S2H = + leads in (13) to 0.16 ![]() 0.5 + 0.3 which
is certainly true, and S2H = - to
0.5 + 0.3 which
is certainly true, and S2H = - to ![]() which is also true.
Then probability arguments indicate that still S2H = + is the more likely
sign. The probability is a function of the magnitudes |UH| and |U2H|
and in this example the probability of S2H = + being correct is
which is also true.
Then probability arguments indicate that still S2H = + is the more likely
sign. The probability is a function of the magnitudes |UH| and |U2H|
and in this example the probability of S2H = + being correct is ![]() .In conclusion the mathematical treatment leads to the same result as the graphic
explanation from the preceding paragraph: the
.In conclusion the mathematical treatment leads to the same result as the graphic
explanation from the preceding paragraph: the ![]() relationship.
relationship.
Copyright © 1984, 1998 International Union of Crystallography
IUCr Webmaster