This is an archive copy of the IUCr web site dating from 2008. For current content please visit
https://www.iucr.org.
![[IUCr Home Page]](/iucr-top/logos/iucrhome.gif)
![[Commission Home Page]](/iucr-top/logos/cteach.gif)


Next: The Positive Quartet Relation
Up: An Introduction to Direct Methods. The
Previous: Large |EH|, |EK| and |E-H-K|: The
The earliest formulation of the triplet-relation (10) for the centrosymmetric
case was via Sayre's equation (Sayre, 1952). This equation can be derived from
Fourier theory as follows.
The electron density can be written as
| 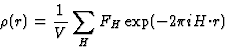 |
(17) |
and upon squaring this function becomes
| 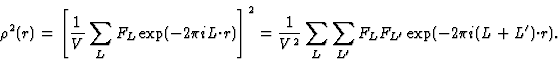 |
(18) |
(18) is rewritten by setting 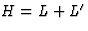 and
and 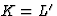 to
to
| 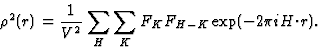 |
(19) |
Because 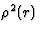 is also a periodic function it can be written, by analogy
with (17), as
is also a periodic function it can be written, by analogy
with (17), as
| 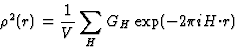 |
(20) |
in which GH is the structure factor of the squared structure. Comparing (19)
and (20) it follows that
| 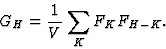 |
(21) |
The structure factor GH is:
| 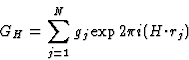 |
(22) |
in which gj is the form factor of the squared atoms. For equal atoms (22)
reduces to
| 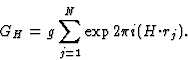 |
(23) |
The normal structure factor for equal atoms is
| 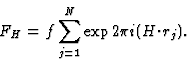 |
(24) |
Thus from (23) and (24) we obtain
| 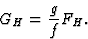 |
(25) |
Finally from (21) and (25) it follows that
| 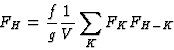 |
(26) |
which is known as Sayre's Equation. It is emphasised that, given an equal-atom
structure, Sayre's equation is exact. The summation (26) contains a large
number of terms; however, in general it will be dominated by a smaller number of
large |FKFH-K|. Rewriting (26) to
| 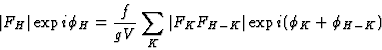 |
(27) |
and considering a reflection with large |FH| it can therefore be assumed that
the terms with large |FKFH-K| have their angular part approximately equal
to the angular part of |FH| itself, illustrated in Fig. 8. For one strong
|FKFH-K| this leads to:
| 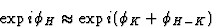 |
(28) |
or
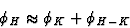
or
| 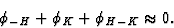 |
(29) |
Relation (29) is identical to (16), the triplet relation. Thus by introducing
the obvious argument that the most important terms in Sayre's equation (27) must
reflect the phase 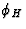 the triplet relation is found.
the triplet relation is found.
In the event that only a number of larger terms in (27) are available the
scaling constant f/gV has no meaning. Nevertheless most likely the phase
information included in these terms is correct and thus an expression such as
| 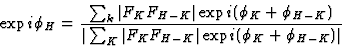 |
(30) |
in which K ranges over a limited number of terms may be very helpful.
The so called tangent formula (Karle and Hauptman, 1956)
| 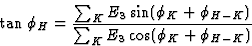 |
(31) |
in which the signs of numerator and denominator are used to determine the
quadrant of the phase 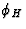 , is closely related to (30). This formula is
used in almost all direct method procedures.
, is closely related to (30). This formula is
used in almost all direct method procedures.


Next: The Positive Quartet Relation
Up: An Introduction to Direct Methods. The
Previous: Large |EH|, |EK| and |E-H-K|: The
Copyright © 1984, 1998 International Union of
Crystallography
IUCr
Webmaster
![[IUCr Home Page]](/iucr-top/logos/iucrhome.gif)
![[Commission Home Page]](/iucr-top/logos/cteach.gif)
![]()
![]()
![]()
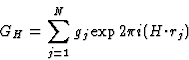
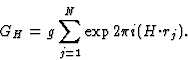
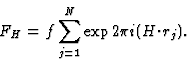
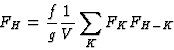
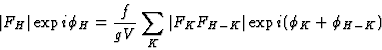
![]()