This is an archive copy of the IUCr web site dating from 2008. For current content please visit https://www.iucr.org.

3. The Intrinsic Symmetry of the Physical Properties

The rank of the tensors determines the numbers of the tensor components. The number of the components of the 0,1,2,3,4,5,6-rank tensors are 1,3,9,27,81,243,729. However, certain symmetries considerably reduce the number of the independent components. These may be intrinsic symmetries, inherent in the physical property, or crystal symmetries, whose effect on the number of the independent components will be discussed in the next section.

In some instances the intrinsic symmetries follow from the definition of the physical property in question. Thus for example in the case of elasticity it follows from the symmetry of the stress and deformation tensors that also the fourth-rank tensor of the second-order elastic stiffnesses [c_ijkl] (see Table 1) is symmetric with respect to the (ij) and (kl) permutations. This way the number of the independent coefficients of the fourth-rank elastic tensor decreases from 81 to 36. Further on from the symmetry of the deformation tensor follows the symmetry of the [d_ijk] piezo-electric tensor (see Table 1) with respect to the commutability of the j and k suffixes, which means that the piezoelectric tensor has not more than 18 independent components.

The symmetries inherent in the physical properties may be in most cases found by thermodynamical reasoning. In case of equilibrium properties, i.e. properties which refer to thermodynamically reversible changes, the intrinsic symmetry of the properties can be disclosed by investigating the thermodynamical potentials. For physical properties characteristic for transport processes the intrinsic symmetry is the consequence of Onsager's principle.

In order to illustrate the thermodynamical discussion of equilibrium properties let us consider a more complicated example from which not only the symmetry of the tensors representing individual physical properties (tensors of elasticity, electric and magnetic susceptibility) but also the relationship among the tensors representing various properties becomes obvious. In the example the elastic, thermo, electric and magnetic effects are investigated simultaneously. Independent variables should be the stress [$\sigma_{kl}$], the electric field [E_k], the magnetic field [H_l] and temperature [T] whereas the deformation [$\varepsilon_{ij}$], the polarization [P_i], the magnetization [M_i] and the entropy [S] are selected as dependent variables. The differentials of the former quantities are obviously connected with the following relationships:

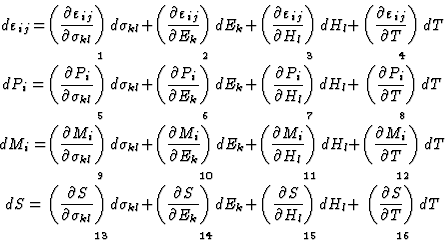$$\begin{array} {@{}c@{}c@{}c@{}c@{}c@{}c} d\varepsilon_{ij} =... ...style13&\scriptstyle14&\scriptstyle15&\scriptstyle16\end{array}$$ (3.1)

The partial derivatives are characteristic of the following effects:

1. Elastic deformation.

2. Reciprocal (or converse) piezo-electric effect.

3. Reciprocal (or converse) piezo-magnetic effect.

4. Thermal dilatation.

5. Piezo-electric effect.

6. Electric polarization.

7. Magneto-electric polarization.

8. Pyroelectricity.

9. Piezo-magnetic effect.

10. Reciprocal (or converse) magneto-electric polarization.

11. Magnetic polarization.

12. Pyromagnetism.

13. Piezo-caloric effect.

14. Electro-caloric effect.

15. Magneto-caloric effect.

16. Heat transmission.

In order to recognize the relationships among the partial derivatives of the equation-system (3.1) let us discuss the Gibb's potential of the system

$$G = U - \sigma_{ij}\varepsilon_{ij} - E_kP_k - H_lM_l - TS.$$ (3.2)

Remembering that the total differential of the internal energy according to the first and second law of thermodynamics is

$$dU = \sigma_{ij} d\varepsilon_{ij} + E_k dP_k + H_l dM_l + T dS$$ (3.3)

one obtains for the total differential of the Gibbs' potential the expression

$$dG = -\varepsilon_{ij}d\sigma_{ij} - P_k dE_k - M_l dH_l - S dT.$$ (3.4)

At the same time one may describe the total differential of the Gibbs' potential with the partial derivatives of the independent variables:

$$dG = \left(\frac{\partial{G}}{\partial\sigma_{ij}}\right) d\... ...l}\right)dH_l + \left(\frac{\partial{G}}{\partial{T}}\right)dT$$ (3.5)

that is

$$\left(\frac{\partial{G}}{\partial\sigma_{ij}}\right) = - \varepsilon_{ij}$$ (3.6)

$$\left(\frac{\partial{G}}{\partial{E}_k}\right) = -P_k$$ (3.7)

$$\left(\frac{\partial{G}}{\partial{H}_l}\right) = -M_l$$ (3.8)

$$\left(\frac{\partial{G}}{\partial{T}}\right) = -S.$$ (3.9)

Investigating the second partial derivatives of the Gibbs' potential and taking into consideration the commutability of the sequence of the partial differentiations one comes to the conclusion that the elastic [s_ijkl], dielectric [$\chi_{jk}$] and diamagnetic susceptibility [$\psi_{kl}$] tensors, as defined by eqs. (3.10)-(3.12) below, are symmetrical

$$- \left(\frac{\partial^2{G}}{\partial\sigma_{kl}\partial\sig... ...= \frac{\partial\varepsilon_{kl}}{\partial\sigma_{ij}}=s_{klij}$$ (3.10)

$$-\left(\frac{\partial^2{G}}{\partial{E}_j\partial{E}_k}\righ... ...E}_j}\right) = \frac{\partial{P}_j}{\partial{E}_k} = \chi_{jk}$$ (3.11)

$$-\left(\frac{\partial^2{G}}{\partial{H}_k\partial{H}_l}\righ... ...}_k}\right) = \frac{\partial{M}_k}{\partial{H}_l} = \psi_{kl}.$$ (3.12)

Moreover, the study of the partial derivatives not only demonstrates the symmetry of the above tensors, but also indicates that the components of the tensors representing the direct and reciprocal effects correspond to each other. Let us investigate the following partial derivatives

$$- \left(\frac{\partial^2{G}}{\partial\sigma_{ij}\partial{E}_... ...rac{\partial \varepsilon_{ij}}{\partial{E}_k}\right) = d_{kij}$$ (3.13)

$$-\left(\frac{\partial^2{G}}{\partial\sigma_{ij}\partial{H}_l... ...frac{\partial \varepsilon_{ij}}{\partial{H}_l}\right)= q_{lij}$$ (3.14)

$$- \left(\frac{\partial^2{G}}{\partial{E}_k\partial{H}_l}\rig... ...\left(\frac{\partial{P}_k} {\partial{H}_l}\right)=\lambda_{lk}$$ (3.15)

$$- \left(\frac{\partial^2{G}}{\partial\sigma_{ij}\partial{T}}... ...rac{\partial \varepsilon_{ij}}{\partial{T}}\right)=\alpha_{ij}$$ (3.16)

$$-\left(\frac{\partial^2{G}}{\partial{T}\partial{E}_k}\right)... ...T}}\right)=\left(\frac{\partial{S}} {\partial{E}_k}\right)=p_k$$ (3.17)

$$-\left(\frac{\partial^2{G}}{\partial{T}\partial{H}_l}\right)... ...}}\right)=\left(\frac{\partial{S}} {\partial{H}_l}\right)=m_l.$$ (3.18)

From the above equations follows that correspondences exist between:

(a) the components of the tensors representing the piezoelectric and reciprocal piezo-electric effect (eq. 3.13)),

(b) the components of the tensors representing the piezo-magnetic and reciprocal piezo-magnetic effect (eq. (3.14)),

(c) the components of the tensors representing the magneto-electric polarization and reciprocal magneto-electric polarization (eq. (3.15)),

(d) the components of the tensors representing the piezo-caloric effect and the thermal dilatation (eq. (3.16)),

(e) the components of the tensors representing the pyroelectric and electrocaloric effect (eq. (3.17)),

(f) the components of the tensors representing the pyromagnetic and magneto- caloric effect (eq. (3.18)).

Integrating equations (3.1) taking into consideration the above statements, and restricting only to the first-order effects, the following system of equations is obtained

$$\varepsilon_{ij}=s_{ijkl}\sigma_{kl}+d_{kij}E_k+q_{lij}H_l+\alpha_{ij}\Delta{T}$$

$$P_k = d_{kij}\sigma{ij}+\chi_{kl}E_l+\lambda_{lk}H_l+p_k\Delta{T}$$ (3.19)

$$M_l = q_{lij}\sigma_{ij}+\lambda_{lk}E_k+\psi_{lm}H_m+m_l\Delta{T}$$

$$\Delta{S} = \alpha_{ij}\sigma_{ij}+p_kE_k+m_lH_l+\frac{c}{T}\Delta{T} \qquad (i,j,k,l = 1, 2, 3).$$

It is perhaps worthwhile to draw the reader's attention to the fact that the system of equations (3.19) represents 16 = 9 + 3 + 3 + 1 equations, the right side of these equations contains 16 terms, since the suffixes occurring twice in each term imply summation according to the Einstein convention. Furthermore the deformation tensor [$\varepsilon_{ij}$] and the stress tensor [$\sigma_{kl}$]are symmetrical, consequently the system of equation (3.19) contains altogether 13 independent equations with 13 independent variables.

As has been pointed out the intrinsic symmetry characteristic for the transport processes is the consequence of Onsager's reciprocal relations. However, it is important to stress that this relation is valid only if the fluxes and the thermodynamical forces connected with them are suitably selected. For simplicity let us study the case of the electrical conductivity. The thermodynamical force [X_k] attached to the electrical current density [j_i] is

$$X_k = \frac{1}{T} \frac{\partial\Phi}{\partial{x}_k} \qquad (k = 1, 2, 3)$$ (3.20)

where $\partial\Phi/\partial{x}_k$ denotes the k-th component of the $\Phi$electrical potential gradient and T is the temperature.

In this case the law of linear current flow is

$$j_i = L_{ik} \frac{1}{T}\frac{\partial\Phi}{\partial{x}_k} \qquad (i,k = 1, 2,3).$$ (3.21)

The expanded form of this equation will be

$$j_1 = L_{11}\frac{1}{T} \frac{\partial\Phi}{\partial{x}_1}+L... ...tial{x}_2}+L _{13}\frac{1}{T}\frac{\partial\Phi}{\partial{x}_3}$$

$$j_2 = L_{21}\frac{1}{T}\frac{\partial\Phi}{\partial{x}_1}+L_... ...rtial{x}_2}+L_{23}\frac{1}{T}\frac{\partial\Phi}{\partial{x}_3}$$ (3.22)

$$j_3 = L_{31}\frac{1}{T}\frac{\partial\Phi}{\partial{x}_1}+L_... ...ial{x}_2}+L_{33}\frac{1}{T}\frac{\partial\Phi}{\partial{x}_3}.$$

According to Onsager's reciprocity relation the L_ik conductivity coefficients are symmetrical with respect to the interchangeability of the suffices, i.e.

L_ik = L_ki.

The relationship between the conductivity coefficients and the components of the specific conductivity tensor [$\sigma_{ik}$] are easily found. The defining equation of the [$\sigma_{ik}$] tensor (see Table 1), is

$$j_i = \sigma_{ik}E_k = -\sigma_{ik}\frac{\partial\Phi}{\partial{x}_k}.$$ (3.24)

However by comparing equations (3.21) and (3.24) one readily sees that

$$L_{ik} = -T\sigma_{ik}.$$ (3.25)

From eqs. (3.23) and (3.25) on the other hand the symmetry of the tensor representing the specific electrical conductivity is quite obvious.

Discussing composite transport processes by some proper selection of the fluxes and thermodynamical forces corresponding to them not only the symmetry of the various tensors, but also the relationships among the tensors representing various properties follow from Onsager's reciprocity relations. For example when discussing the thermoelectric effects the symmetry of the electrical and thermal conductivity tensors follow from Onsager's principle as well as the relationships between the tensors representing the Seebeck effect [$\beta_{ik}$]and the Peltier tensor [$\pi_{ik}$] (see Table 1).

$$T \cdot \beta_{ik} = \pi_{ik}.$$ (3.26)

Additionally it should be remarked that the relationship between the conductivity coefficients in the presence of ($\=H$) magnetic field takes the form

$$L_{ik}(\=H) = L_{ki}(-\=H).$$ (3.27)

Copyright © 1984, 1998 International Union of Crystallography