4. Neumann's Principle

It has been demonstrated in the previous section that the intrinsic symmetry of the physical properties decreases the number of the independent tensor components. Further reduction of the independent components of a physical property tensor, and the zero value of certain components follow from the fact that the crystal symmetry exerts some influence on the symmetry of the physical properties. This fact is expressed by Neuman's principle formulated already in the 19th century according to which the symmetry elements of any physical property of a crystal must include all the symmetry elements of the point group of the crystal :

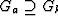$\begin{displaymath} G_a \supseteq G_k\end{displaymath}$

(4.1)

where G_k denotes the symmetry group of the crystal, G_a is the symmetry group of the tensor representing the physical property, the sign $\supset$ indicates that the subgroup belongs to the group. The symmetry group of the crystal refers generally to the 32 point groups derived from the crystal forms, however, sometimes also the recently introduced 90 magnetic or more generally the 122 Shubnikov groups (see [10-14]) should be considered. According to Neumann's principle the tensor representing any physical property should be invariant with regard to every symmetry operation of the given crystal class. The condition of invariance reduces the number of the independent tensor components, since it signifies relationships between the tensor components. In order to describe these relationships it is necessary to discuss the transformation of the tensor components to some extent.

The well-known equations of transformation from an orthogonal x₁, x₂, x₃ system to another similarly orthogonal $x^{\prime}_1, x^{\prime}_2, x^{\prime}_3$ system are for first-, second-, third- and fourth-rank polar tensors according to their definition:

$\begin{displaymath} T^{\prime}_{ij} = a_{ik}a_{jl}T_{kl} \end{displaymath}$

(4.3)

$\begin{displaymath} T^{\prime}_{ijk} = a_{il}a_{jm}a_{kn}T_{lmn} \end{displaymath}$

(4.4)

$\begin{displaymath} T^{\prime}_{ijkl} = a_{im}a_{jn}a_{ko}a_{lp}T_{mnop} \end{displaymath}$

(4.5)

which leads us to the general polar-tensor transformation notation expressed in the equation:

$\begin{displaymath} T^{\prime}_{ijk...n} = a_{ip}a_{jq}a_{kr}\dots a_{nu}T_{pqr...u} \end{displaymath}$

(4.6)

where the a_ij direction cosines are the elements of the (a_ij) matrix. The (a_ij) matrix connects the original and the `new' co-ordinates according to the matrix equation

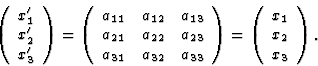$\begin{displaymath} \left(\begin{array} {c} x^{\prime}_1\\ x^{\prime}_2\\ x^{\pr... ...ght)=\left(\begin{array} {c}x_1\\ x_2\\ x_3\end{array}\right). \end{displaymath}$

(4.7)

In some cases the tensor describing the physical properties is not polar, but axial (as for instance the tensor describing the optical activity or piezomagnetism). For axial (or pseudo) tensors the following transformation relation may be used as definition

$\begin{displaymath} T^{\prime}_{ijk...n} = \vert a_{ij}\vert a_{ip}a_{jq}a_{kr}\dots a_{nu}T_{pqr...u} \end{displaymath}$

(4.8)

where |a_ij| denotes the value of the determinant of the matrix (a_ij) whose value is (+1) if the transforming operation consists of pure rotation and (-1) if besides rotation the transformation contains also an inversion, which means that the symmetry operation changes also the hand of the axes.

It is not difficult to find out whether the tensor representing any physical property is polar or axial, since this can be easily decided by the eq. (2.1) defining the physical property in question. If only one of the tensors [A_pqr...u] and [B_ijk...n] in eq. (2.1) is axial (for instance magnetic field is an axial tensor of rank one) also the property tensor [a_{ijk...npqr...u}] as defined by eq. (2.1) will be axial, in every other case the tensor is polar.

It should be remarked that if also the magnetic point groups are considered eq. (4.6) and eq. (4.8) expressing the transformation properties of the tensor components are valid only for conventional symmetry operations. If, however, the conventional symmetry operations are combined with time-inversion which actually happens in anti-symmetry operations (see [10-14]) the right sides of eqs. (4.6) and (4.8) respectively should be multiplied with (-1) whenever eq. (2.1) defining the physical properties contains the magnetic vector quantities (magnetic field, magnetic induction, magnetization vector) odd times. Tensors representing this type of properties are called C-tensors.¹ For a more detailed discussion of this problem the reader is referred to the literature.^1-3

Considering the equations of transformation (4.6) and (4.8) and with regard to the above remark, the relationships between the components of the polar and axial tensors for a given crystal class can now be defined, since the invariance of a tensor with regard to any symmetry operation requires the relationship

$\begin{displaymath} T^{\prime}_{ijk...n} = T_{ijk...n}. \end{displaymath}$

(4.9)

Thus in case of polar tensors, if the matrix (a_ij) describes any conventional symmetry operation of a given crystal class, the tensor components must according to the Neumann's principle satisfy the equation

$\begin{displaymath} T_{ijk...n} = a_{ip}a_{jq}a_{kr}\dots a_{nu}T_{pqr...u} \end{displaymath}$

(4.10)

whereas considering the condition of the invariance of axial tensors taking into account the eqs. (4.8) and (4.9) one may write

$\begin{displaymath} T_{ijk...n} = \vert a_{ij}\vert a_{ip}a_{jq}a_{kr}\dots a_{nu}T_{pqr...u} \end{displaymath}$

(4.11)

Of course in the case of antisymmetry operations and the previously discussed C-tensors the right-hand side of the eqs. (4.10) and (4.11) are multiplied with (-1).

For every tensor component an equation of the type (4.10) and (4.11) respectively should be valid so that the tensor components must satisfy a system of these equations. Since this holds for every symmetry operation of a given crystal class, the number of the systems of equations between the tensor components will be equal to the number of the symmetry operations which may be performed in the given crystal class. However, in order to obtain every relationship among the components of a tensor representing any physical property in case of a given crystal class, it is not necessary to write down for every symmetry operation the system of equations of the type (4.10) and (4.11) respectively. It is well known from the group theory that for various crystal classes every symmetry operation may be deduced from a few basic symmetry operations. The application of the matrices corresponding to these basic operations (the generating matrices) are sufficient to obtain the effect due to the symmetry of a crystal class on the given tensor in question. Tables 2 and 3 summarize a series of generating matrices for every conventional crystal class.

These interrelations appear to be at first instance somewhat complicated, a simple example, however, will help to obtain a better understanding. Let us consider the form of the pyroelectric tensor in the crystal class 3 of the trigonal system assuming that the x₃ axis of the coordinate system is the three-fold rotation axis. As one may see on consulting Tables 2 and 3 the coordinate transformation related to the symmetry operation can be described with the following matrix

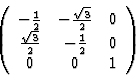$\begin{displaymath} \left(\begin{array} {ccc} -\frac{1}{2}&-\frac{\sqrt{3}}{2}&0\\ \frac{\sqrt{3}}{2}&-\frac{1}{2}&0\\ 0&0&1\end{array}\right) \end{displaymath}$

(4.12)

Taking into consideration the condition of invariance of the polar tensor as expressed in eq. (4.10) one obtains for the tensor components the following equations

$\begin{displaymath} p_1 = -\frac{1}{2}p_1-\frac{\sqrt{3}}{2}p_2\end{displaymath}$

$\begin{displaymath} p_2=\frac{\sqrt{3}}{2}p_1-\frac{1}{2}p_2\end{displaymath}$

(4.13)

**Table 2:** The generating matrices of the 32 point groups (crystal classes). After Koptsik¹³

Crystal system	Class symbol		Generating matrices	No. of symmetry elements	The choice of x₁, x₂, x₃ crystal physical axes in relation to the symmetry axes

	International	Schoenflies

Triclinic	1	C₁	M₀	1
	$\=1$	S₂=C_i	M₁	2
Monoclinic	2	C₂	M₂	2
	m	C_1h=C_s	M₃	2	$x_3 \parallel 2 \mbox{ or }\=2$
	2/m	C_2h	M₂, M₃	4
Orthorhombic	222	V=D₂	M₄, M₂	4	$x_1 \parallel 2\mbox{ or }\=2$
	mm2	C_2v	M₅, M₂	4	$x_2 \parallel 2\mbox{ or }\=2$
	mmm	V_h=D_2h	M₅, M₆, M₃	8	$x_3 \parallel 2$
Tetragonal	4	C₄	M₇	4
	$\=4$	S₄	M₈	4
	422	D₄	M₇, M₄	8	$x_1 \parallel 2\mbox{ or }\=2$
	4/m	C_4h	M₇, M₃	8	$x_2 \parallel 2\mbox{ or }\=2$
	4mm	C_4v	M₇, M₅	8	$x_3 \parallel 4\mbox{ or }\=4$
	$\=42m$	V_d=D_2d	M₈, M₄	8
	4/mmm	D_4h	M₇, M₃, M₅	16
Trigonal	3	C₃	M₉	3
	$\=3$	S₆=C_3i	M₁₀	6	$x_1 \parallel 2\mbox{ or }\=2$
	32	D₃	M₉, M₄	6	$x_2 \perp 2\mbox{ or }\=2$
	3m	C_3v	M₉, M₅	6	$x_3 \parallel 3\mbox{ or }\=3$
	$\=3m$	D_3d	M₁₀, M₅	12
Hexagonal	6	C₆	M₁₁	6
	$\=6$	C_3h	M₁₂	6
	$\=6m2$	D_3h	M₁₂, M₅	12	$x_1 \parallel 2\mbox{ or }\=2$
	622	D₆	M₁₁, M₄	12	$x_2 \perp 2\mbox{ or }\=2$
	6/m	C_6h	M₁₁, M₃	12	$x_3 \parallel 6 \mbox{ or }\=6$
	6/mm	C_6v	M₁₁, M₅	12
	6/mmm	D_6h	M₁₁, M₅, M₃	24
Cubic	23	T	M₁₃, M₂	12	$x_1 \parallel 2$
	m3	T_h	M₁₄, M₂	24	$x_2 \parallel 2, x_3 \parallel 2$
	432	O	M₁₃, M₇	24	$x_1 \parallel 4\mbox{ or }\=4$
	$\=43m$	T_d	M₁₃, M₈	24	$x_2 \parallel 4\mbox{ or }\=4$
	m3m	O_h	M₁₄, M₇	48	$x_3 \parallel 4\mbox{ or }\=4$

**Table 3:** Generating matrices

	identity

inversion		fourfold inversion-rotation about x₃ axis
twofold rotation about x₃ axis		threefold rotation about x₃ axis
reflection in x₁x₂ plane		threefold inversion-rotation about x₃ axis
twofold rotation about x₁ axis		sixfold rotation about x₃ axis
reflection in x₂x₃ plane		sixfold inversion-rotation about x₃ axis
reflection in x₁x₃ plane		threefold rotation about [111] direction
fourfold rotation about x₃ axis		threefold inversion-rotation about [111] direction

The method used in this example may be applied in every case, though with higher rank tensors it may be in many cases rather tiresome.

Considerable time can be saved (with the exception of the trigonal and hexagonal classes) by the direct inspection method worked out by Fumi,⁴, which though in principle not differing from the previous treatment leads to results in a relatively short time. Fumi's method is based on the fact that in an orthogonal coordinate system the polar tensor components transform in the same way as the products of the corresponding coordinates (see eq. (4.6)). One must, however, be careful not to commute the sequence of the factors, thus for instance instead of the product x₁x₂ one cannot write x₂x₁.

Fumi's method may be studied by a simple example considering the form of a polar second-rank tensor, e.g. the dielectric susceptibility tensor of the crystal class 2 of the monoclinic system. Assuming that the two-fold symmetry axis coincides with the x₂ coordinate axis the symmetry operator will transform the coordinates in the following way

$\begin{displaymath} x_1 \rightarrow -x_1 \qquad x_2 \rightarrow x_2 \qquad x_3 \rightarrow -x_3\end{displaymath}$

(4.14)

or in a more concise way

$\begin{displaymath} 1 \rightarrow -1 \qquad 2 \rightarrow 2 \qquad 3 \rightarrow -3\end{displaymath}$

(4.15)

From this it follows that

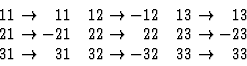$\begin{displaymath} \begin{array} {ccc} 11 \rightarrow \phantom{-}11 & 12 \right... ... & 32 \rightarrow -32 & 33 \rightarrow \phantom{-}33\end{array}\end{displaymath}$

(4.16)

that is

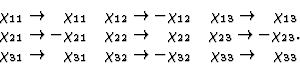$\begin{displaymath} \begin{array} {ccc} \chi_{11} \rightarrow \phantom{-}\chi_{1... ...i_{32} & \chi_{33} \rightarrow \phantom{-}\chi_{33}\end{array} \end{displaymath}$

(4.17)

At the same time as a consequence of Neumann's principle every component should be transformed into itself therefore

$\begin{displaymath} \begin{array} {cc} \chi_{12} = -\chi_{12} = 0 & \chi_{21} = ... ...{23} = -\chi_{23} = 0 & \chi_{32} = -\chi_{32} = 0.\end{array} \end{displaymath}$

(4.18)

Thus for class 2 of the monoclinic system the electric susceptibility tensor has the form

$\begin{displaymath} \left[\begin{array} {ccc} \chi_{11} & 0 & \chi_{13}\\ 0 & \chi_{22} & 0\\ \chi_{31} & 0 & \chi_{33}\end{array}\right]\end{displaymath}$

(4.19)

In the case of dielectric susceptibility as a result of the intrinsic symmetry $\chi_{31}$ is equal to $\chi_{13}$ i.e. the tensor (4.19) is symmetrical.

The forms of tensors or matrices composed of tensor components for the various crystal classes can be found properly tabulated in the special literature, see for example [1, 2, 5-7, 16, 17].

Finally it should be observed that in some cases simple geometric considerations enable the determination of the independent components of the tensors representing the physical properties. It is easy to see that no pyroelectric effect can exist in a crystal possessing a centre of symmetry. This means that for these crystals every component of the pyroelectric tensor is zero, p = [0, 0, 0], because in these crystals if the vector of polarization were pointed in a given direction the vector should appear also in the opposite direction as a result of Neumann's principle, consequently its value can only be zero.