 |
![[IUCr Home Page]](/iucr-top/logos/iucrhome.gif)
![[Commission Home Page]](/iucr-top/logos/cteach.gif)
We will examine in turn what happens when X-rays strike a single atom, when a plane wave front of X-rays strikes a line of atoms, when a beam of X-rays strikes a two-dimensional net of atoms and finally a 3-dimensional lattice of atoms.
When a wavefront of X-rays strikes an atom, the electrons in that atom
interact with the X-rays and immediately re-emit the X-radiation, normally
without change of wavelength, and the X-radiation that is emitted
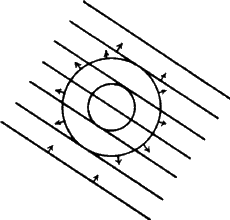
by the atom is emitted as a spherical wavefront (Fig. 12). This, of course,
is an ideal situation which we cannot observe in practice. Consider a line
of identical atoms, distance a apart. Let a beam of wavelength ![]() strike this line of atoms at an angle
strike this line of atoms at an angle ![]() . Each of these atoms
immediately begins to emit radiation in the form of spherical wavefronts
(Fig. 13). If one observes the scattered radiation in the plane of the
incident beam and scans all possible angles, the requirement for seeing a beam
of enhanced intensity is that the path-length difference between the advancing
incident wavefront and the advancing diffracted wavefront shall be a whole
number of wavelengths.
. Each of these atoms
immediately begins to emit radiation in the form of spherical wavefronts
(Fig. 13). If one observes the scattered radiation in the plane of the
incident beam and scans all possible angles, the requirement for seeing a beam
of enhanced intensity is that the path-length difference between the advancing
incident wavefront and the advancing diffracted wavefront shall be a whole
number of wavelengths.
Consider Fig. 14. The length PR-OQ should be equal to n![]() wavelength
wavelength ![]() . If that situation holds, then the observer looking along
the lines of the arrows will see that the scattered radiation is very intense at
that angle: there is constructive interference. If the observer moves away
from that particular angle there will be no enhanced scattered radiation.
It is important to notice that, while the sketch is two-dimensional, each
atom is giving off a spherical wave of radiation. The directions of
scattering thus constitute the surface of a series of cones (see Fig. 15).
The largest cone angle corresponds to a difference of one wavelength
between the incident and the diffracted radiation. The angle of deviation
increases and the cone angle decreases as the integer becomes 1, 2, 3 and
so on. It is fairly obvious that for cosine
. If that situation holds, then the observer looking along
the lines of the arrows will see that the scattered radiation is very intense at
that angle: there is constructive interference. If the observer moves away
from that particular angle there will be no enhanced scattered radiation.
It is important to notice that, while the sketch is two-dimensional, each
atom is giving off a spherical wave of radiation. The directions of
scattering thus constitute the surface of a series of cones (see Fig. 15).
The largest cone angle corresponds to a difference of one wavelength
between the incident and the diffracted radiation. The angle of deviation
increases and the cone angle decreases as the integer becomes 1, 2, 3 and
so on. It is fairly obvious that for cosine ![]() and it is this condition which tells you the maximum number of cones that will
be observable from a line of atoms of spacing d for radiation of
wavelength
and it is this condition which tells you the maximum number of cones that will
be observable from a line of atoms of spacing d for radiation of
wavelength ![]() . Consider now a second line of atoms at some angle to the
first line: a two-dimensional net. Consider the second line of atoms quite
independently from the first line and it is fairly obvious that the second
line of atoms when irradiated by the X-rays will generate a series of cones
also obeying the same criteria. Thus the two-dimensional net will behave
as if it were simply two lines of atoms and produce two families of
intersecting cones. It should be fairly obvious that for two sets of cones
with a common origin but with their axes non-collinear, the intersection
of these cones will consist of a series of lines. Thus, for a two-dimensional
net, very strong constructive interference will be seen only along certain
well defined directions in space, and no longer anywhere along the
surface of the cone as was observed for one line of atoms (see Fig. 16).
. Consider now a second line of atoms at some angle to the
first line: a two-dimensional net. Consider the second line of atoms quite
independently from the first line and it is fairly obvious that the second
line of atoms when irradiated by the X-rays will generate a series of cones
also obeying the same criteria. Thus the two-dimensional net will behave
as if it were simply two lines of atoms and produce two families of
intersecting cones. It should be fairly obvious that for two sets of cones
with a common origin but with their axes non-collinear, the intersection
of these cones will consist of a series of lines. Thus, for a two-dimensional
net, very strong constructive interference will be seen only along certain
well defined directions in space, and no longer anywhere along the
surface of the cone as was observed for one line of atoms (see Fig. 16).
To extend this idea into three dimensions you need only add another line of atoms non-coplanar with the first net. Irradiate this line of atoms with the X-ray beam and, as before, a series of cones is formed. This family can only have a line of intersection common with those of the first two under the special condition that UV and W are coincident (see Fig. 17). The result is that, for a three dimensional lattice of atoms irradiated by X-radiation, strong constructive interference will only occur in specific directions and for specific conditions of incidence. In other words one will not observe constructive interference unless one stands exactly in the right place in space. This type of construction was done by Laue about 1912. Although it is mathematically very straightforward, it is very difficult to picture in three-dimensions what is going on. Fortunately for us, Bragg in 1913 saw that the conditions for constructive interference of X-rays were equivalent to that of a simple plane reflecting the X-ray radiation with the condition that the plane could be described by a triplet of Miller indices. We can take any plane (hkl) in our crystal and we will now consider not spacings between atoms or lattice points, but spacings between the planes.
Consider Fig. 18. The incident X-radiation strikes the planes (hkl) at
an angle ![]() . The spacing between these planes is d. We will assume that
the X-rays are reflected in exactly the same way as light will be reflected
from a mirror so that the reflected beam leaves the plane at angle
. The spacing between these planes is d. We will assume that
the X-rays are reflected in exactly the same way as light will be reflected
from a mirror so that the reflected beam leaves the plane at angle ![]() . The
requirement for constructive interference is very simple. Once again it is
that the path length difference between the incoming and the outgoing
beams should be a whole number of wavelengths. It is very easy to show
that the path difference is equal to
. The
requirement for constructive interference is very simple. Once again it is
that the path length difference between the incoming and the outgoing
beams should be a whole number of wavelengths. It is very easy to show
that the path difference is equal to ![]() and the final result is
and the final result is ![]() . This is called Bragg's
law, and it is of considerable importance in X-ray crystallography. The
maximum value that
. This is called Bragg's
law, and it is of considerable importance in X-ray crystallography. The
maximum value that ![]() will ever have is 1. For
will ever have is 1. For ![]() and the X-ray strikes perpendicular to the
face of the crystal and is reflected back along the incident path. For this
case,
and the X-ray strikes perpendicular to the
face of the crystal and is reflected back along the incident path. For this
case, ![]() ; the minimum d-spacing that we can ever observe with
X-rays in any crystal will be equal to one half of the incident wavelength
of the X-rays. What is interesting here, is that Bragg included the
numerical value n (the integer) because he chose planes whose Miller
indices (hkl) were prime numbers. In other words, Bragg's planes would
be called (111) but never (222) or (333). This followed the normal
conventions used in geology. He would talk about the plane (111) and
then he would consider the n in the equation to be the 1st, 2nd, 3rd, 4th
and so on order of reflection from that plane. For the single crystal X-ray
crystallographer the numerical value of n is normally said to be equal to 1
and then we would simply use the equation
; the minimum d-spacing that we can ever observe with
X-rays in any crystal will be equal to one half of the incident wavelength
of the X-rays. What is interesting here, is that Bragg included the
numerical value n (the integer) because he chose planes whose Miller
indices (hkl) were prime numbers. In other words, Bragg's planes would
be called (111) but never (222) or (333). This followed the normal
conventions used in geology. He would talk about the plane (111) and
then he would consider the n in the equation to be the 1st, 2nd, 3rd, 4th
and so on order of reflection from that plane. For the single crystal X-ray
crystallographer the numerical value of n is normally said to be equal to 1
and then we would simply use the equation ![]() but the
d in the equation would be for a plane whose Miller indices can be either
prime numbers or non-prime. Notice something else about the Bragg equation.
Theta is a variable, in other words it is an angle which you can choose
simply by rotating the crystal relative to the X-ray beam. The wavelength
has a fixed value and d is obviously a fixed value determined by the size
of the unit cell and the Miller indices. If we write down the equation as
but the
d in the equation would be for a plane whose Miller indices can be either
prime numbers or non-prime. Notice something else about the Bragg equation.
Theta is a variable, in other words it is an angle which you can choose
simply by rotating the crystal relative to the X-ray beam. The wavelength
has a fixed value and d is obviously a fixed value determined by the size
of the unit cell and the Miller indices. If we write down the equation as
![]() and fix
and fix ![]() in our experiment, we see that the experimentally
observed value of
in our experiment, we see that the experimentally
observed value of ![]() is a direct measure not of the d spacing but
of the reciprocal of the d spacing of the planes. Notice also that somehow or
other we are looking at perpendiculars to these planes because this d
spacing is the perpendicular distance between planes of the crystal. For
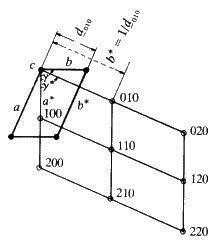
this reason, Ewald (1912) constructed what he called a reciprocal lattice.
A reciprocal lattice is merely a construction that consists of normals
drawn to all possible lattice planes whose indices are (hkl). These normals
radiate from a common origin (the point 0, 0, 0 in the unit cell) and each
normal terminates at a distance from the origin, proportional to the
reciprocal of the d-spacing of the plane (hkl). Consider Fig. 19. What is
interesting about it, is that each family of planes whose Miller indices are
(hkl) is described by only one point in the reciprocal lattice: you may
have an infinite number of planes of indices (hkl) but they correspond to
one point (hkl) in the reciprocal lattice. The geometrical relationship
between real lattices and unit cells and these reciprocal lattices and
reciprocal cells are fairly complex. They will not help us directly with the
applications that we want to consider in this article, therefore it is best
that we stop the discussion of reciprocal lattices at this point and proceed
to some other aspects of X-rays and interactions of X-radiation with
crystals.
is a direct measure not of the d spacing but
of the reciprocal of the d spacing of the planes. Notice also that somehow or
other we are looking at perpendiculars to these planes because this d
spacing is the perpendicular distance between planes of the crystal. For
this reason, Ewald (1912) constructed what he called a reciprocal lattice.
A reciprocal lattice is merely a construction that consists of normals
drawn to all possible lattice planes whose indices are (hkl). These normals
radiate from a common origin (the point 0, 0, 0 in the unit cell) and each
normal terminates at a distance from the origin, proportional to the
reciprocal of the d-spacing of the plane (hkl). Consider Fig. 19. What is
interesting about it, is that each family of planes whose Miller indices are
(hkl) is described by only one point in the reciprocal lattice: you may
have an infinite number of planes of indices (hkl) but they correspond to
one point (hkl) in the reciprocal lattice. The geometrical relationship
between real lattices and unit cells and these reciprocal lattices and
reciprocal cells are fairly complex. They will not help us directly with the
applications that we want to consider in this article, therefore it is best
that we stop the discussion of reciprocal lattices at this point and proceed
to some other aspects of X-rays and interactions of X-radiation with
crystals.
 |
We accept at this stage that any set of planes in a crystal will cause a reflection of the X-ray beam if the set of planes is set at the right angle to the incident X-ray beam. The question now is how strongly will this set of planes reflect the X-rays? Will they necessarily reflect the incoming beam strongly or will they reflect it fairly weakly? The intensity of the reflected beam will be proportional to the product of the intensity of the incident beam and the concentration or density of electrons in the plane that is reflecting the beam. Note: It is the concentration of electrons , not of atoms, because it is the electrons surrounding the atoms that cause the scattering of the X-rays. It should be obvious that, if we know the size of the unit cell and if we know exactly where all the atoms are in that unit cell and if we know the atomic number of each of these atoms (in other words if we know how many electrons are associated with each atom in that cell), we should be able to calculate for any chosen plane with Miller indices (hkl) exactly what the concentration of electrons in that plane will be. In other words, if we know the structure of the unit cell, we should be able to calculate the intensity with which any chosen plane in that cell will scatter X-rays. In fact, this is very easy to do and the name given to such a calculated value is the Structure Factor.
Consider the reverse situation. Imagine that we know the size of the unit cell and that we can measure the intensities of reflection from all possible planes. It appears that from this information we should be able to calculate the positions of the atoms in the cell and not only that, but also the relative number of electrons per atom. The problem of working out where the atoms are in the unit cell from the observed d-spacings and intensities of reflection is called `solving a crystal structure'. This is one thing we will not attempt to do in this course, because what may sound very easy is, in fact, extremely complicated under some circumstances. All that is important at this stage, is to bear in mind that the intensity with which any family of planes can reflect an X-ray beam is directly proportional to the concentration of electrons in those planes. It is obvious that all compounds whose formulae are different, or whose unit cells are different, must have a different collection of possible d-spacings and of different intensities of reflection. The combination of different d-spacings and different intensities is characteristic of any crystalline material and we can use the observed pattern of spacings and intensities of the reflections as a way of identifying an unknown compound in a specific crystalline phase. It will be as characteristic of a particular crystal structure as a fingerprint is of a specific person.
Copyright © 1981, 1997 International Union of Crystallography
IUCr Webmaster