
![[IUCr Home Page]](/iucr-top/logos/iucrhome.gif)
![[Commission Home Page]](/iucr-top/logos/cteach.gif)
Vectors are objects which are encountered everywhere in crystallography: as distance vectors between atoms, as basis vectors of the coordinate system, as translation vectors of a crystal lattice, as vectors of the reciprocal lattice, etc. They are elements of the vector space which is studied by linear algebra and is an abstract space. However, vectors can be interpreted easily visually, see Fig.1.3.1:
 |
For each pair of points X and Y one can draw the arrow
![]() from X to Y. The arrow
from X to Y. The arrow
![]() is a representation of the vector
r, as is any arrow of the direction and length of r,
see Fig. 1.3.1. The set of all vectors forms
the vector space. The vector
space has no origin but instead there is the zero vector
or o vector
is a representation of the vector
r, as is any arrow of the direction and length of r,
see Fig. 1.3.1. The set of all vectors forms
the vector space. The vector
space has no origin but instead there is the zero vector
or o vector
![]() which is obtained by connecting any point
which is obtained by connecting any point ![]() with itself. The vector
r has a length
which is designed by
with itself. The vector
r has a length
which is designed by
![]() , where
r is a non-negative real number. This number is also called the
absolute value of the vector.
A formula for the calculation of
, where
r is a non-negative real number. This number is also called the
absolute value of the vector.
A formula for the calculation of ![]() can be found in
Sections 1.6 and 2.6.
can be found in
Sections 1.6 and 2.6.
For such vectors some simple rules hold which can be visualized, e.g. by a drawing in the plane:
In particular,
![]() is a
vector of length 1. Such a vector is called a unit vector.
Further
is a
vector of length 1. Such a vector is called a unit vector.
Further
![]() ;
;
![]() is the zero-vector with length 0. It is the only vector
with no direction.
is the zero-vector with length 0. It is the only vector
with no direction.
![]() is that vector which
has the same length as r,
is that vector which
has the same length as r,
![]() , but
opposite direction.
, but
opposite direction.

Fig. 1.3.2 Visualization of the commutative
law of vector addition:
|
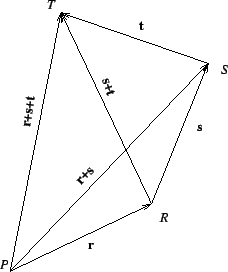 Fig. 1.3.3 Visualization of the associativity
of vector addition:
Fig. 1.3.3 Visualization of the associativity
of vector addition:
|
Definition (D 1.3.2) A set of ![]() vectors
vectors ![]() ,
, ![]() ,
...,
,
..., ![]() is called linearly independent if the equation
is called linearly independent if the equation
In the plane any 3 vectors r![]() , r
, r![]() , and r
, and r![]() are linearly dependent because coefficients
are linearly dependent because coefficients ![]() can always be found
such that
can always be found
such that ![]() not all zero and
not all zero and
Definition (D 1.3.2) The maximal number of linearly independent vectors in a vector space is called the dimension of the space.
As is well known, the dimension of the plane is 2, of the space is 3. Any 4
vectors in space are linearly dependent. Thus, if there are 3 linearly
independent vectors r![]() , r
, r![]() , and r
, and r![]() , then
any other vector r can be represented in the form
, then
any other vector r can be represented in the form
![]()
Such a representation is widely used, it will be considered in the next section.
Copyright © 2002 International Union of Crystallography
IUCr Webmaster