4.7. BAYEST: Bayesian estimates of |I| and |F|
Author: Nick Spadaccini, Computer Science Department, University of Western Australia, Nedlands, WA 6907, Australia
BAYEST determines a posterior intensity and/or structure factor modulus and the associated standard deviations. The program is useful in the treatment of weak or negative intensities. The calculation is based on the work of French and Wilson (1978), and the user should refer to the original paper for details of the method.
4.7.1. Introduction
Intensity measurements which are negative are generally either excluded from the data set or are reset to zero. Both these practices result in biased determinations of the structure. This bias may be overcome by including all reflections in a refinement based on F2. However, for refinements based on F(rel) it is essential to obtain the best possible estimates to the structure factor modulus and its standard deviation.
A more adequate treatment of negative or weak intensities is required. Setting the structure factor to zero ignores the information present in the observation of a negative intensity (i.e. it is weak). Assuming the intensity distribution of data follows the Wilson distribution, and that the true intensity is constrained to be non-negative, a posterior estimate of I or F(rel) and their standard deviations can be made.
4.7.2. Intensity Measurements And Bayes Theorem
When prior information is known, say from a physical model, about an
experimental measurement one has a starting point from which to infer a better
estimate of the observation from the data. A useful method of employing prior
knowledge is in the Bayesian approach to inference where the probability
distribution is regarded as a measure of information and represents our degree
of belief rather than just relative frequencies. Our interest lies in
determining the best estimate of the intensity, denoted J. The experimentally
measured intensity I and its variance 
2(I) are
subject to
counting and statistical error. What must be determined is the probability
distribution of J given the observation I. The prior probability distribution
of J, p(J), is assumed to be the appropriate Wilson distribution. The
likelihood distribution for I, p(I | J), is assumed to be normal with mean J and
variance 2(I). Bayes theorem states that the
posterior probability distribution of J given the observation I is:
p(J | I) = k p(J) p(I | J)
where p(J) = W(J,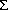
) and p(I | J) = N(J, 2(I))
The posterior estimates for I and its esd are given by the following expectation values:
E(J) =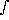 
J p(J | I) dJ
E(2(J)) = 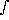(J - E(J))2 p(J | I) dJ
The posterior estimates of F(rel) and 2(F) may
be derived from E(J) and E(2(J)) or from the
expectation values:
E(F) = 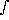F p(J | I) dJ
E(2(F)) = 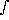(F - E(F))2 p(J | I) dJ
4.7.3. The Wilson Parameter (S)
The prior distribution of J assumed requires knowledge of the Wilson parameter,
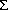. Assuming the data collected contains a fair number of observations,
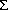is determined from the mean value of F2 in shells of
s2 (where s=sin
/
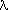). The user may specify the number of
shells the data is to be divided into through the nrange option
in the BAYEST line. The default is 50 shells.
The program searches the bdf for items in a hierarchial manner. The priority
item is F2. If this is present, the distribution of mean
F2 versus s2 is calculated and the appropriate values of
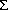determined. If I and Lp corrections are found, F2 is
generated and the distribution determined. If any of these items are present
their esds must also be present.
The user can apply the correction to F(rel) only, leaving the other items as they were input. Otherwise all items present are corrected. The value of F(rel) may be corrected in one of the two following ways.
Requesting the int option and having F(rel) present on the bdf. In this case the corrected F(rel) is derived from the corrected I or F2.
Explicitly requesting F(rel) to be corrected only. In this case the corrected F(rel) and
(F) are derived from the expectation
values E(F) and E(2(F)).
The number of shells should be chosen so that there are sufficient reflections in each shell so that a reasonable determination of the distribution may be made (150-200 or reflections per shell).
4.7.4. Input Output
BAYEST is a two pass operation. The first pass determines the data set distribution and the second pass applies the Bayesian corrections. Items which MUST be present on the bdf are the maximum and minimum values of s, s for each reflection, and either of intensity and Lp, or F2. No expansion to the bdf is made. The items input are also output, though the user has the option to apply the correction as desired.
4.7.5. File Assignments
Reads reflection data from the input archive bdf
Writes corrected reflection data to the output archive bdf
4.7.6. Example
In this run the data is divided into 35 groups and the correction is applied to
F(rel) only leaving the other items uncorrected. The printing is suppressed.
Note that F(rel) and (F) must be present in the input bdf. BAYEST does
not expand the bdf by generating F(rel) from I or F2. That is left
to ADDREF.