4.26. GENSIN: Generate triplets and quartets
Authors: V. Subramanian and Syd Hall
Contact: Syd Hall, Crystallography Centre, University of Western Australia, Nedlands 6907 Australia
GENSIN generates triplet and quartet structure invariant relationships. Group structure factor information entered from the input bdf (from GENEV) can be used to enhance the conditional probabilities of invariant relationships and to improve the estimate of their expected phase value.
4.26.1. Introduction
Most direct methods approaches use the triplet structure invariant relationship
3 = 
(h1) +
(h2) +(h3)
where h1 + h2 + h3 = 0 (1)
The value of 3 is conditional on the
probability expression
A = 2 a |E(h1) E(h2) E(h3)| where
a = 
N f3 / ( Nf2)
3/2 (2)
N is the number of atoms in the unit cell. For uniform-atom structures a
tends to 1/N1/2. The probability distribution of
3, conditional on A, (Cochran, 1955) is
P(3 | A) = exp(A cos 3)
2
I0(A) (3)
The importance of the magnitude of A (and therefore the E-values and N) may be
seen from the variation of P(3|A) for the typical values of
A.
3 and on being able to apply triplet relationships as a
series of equations. For large values of A, 3 has a high
probability of being 0. and this makes large-A triplets particularly important
for these processes.For the quartet structure invariant relationship
4 = (h1) + (h2) +
(h3) + (h4) where
h1+h2+h3+h4 = 0 (4)
the value of 4 depends principally on the probability factor
B = 2b |E(h1) E(h2) E(h3)
E(h4)| where b = N f4 /
(N f2)2 (5)
For uniform-atom structures b tends to 1/N. The probability distribution
of 4, ignoring the cross-vectors magnitudes
E(h1+h2), E(h1+h3), and
E(h1+h4) (referred to later as
E12,E13,E14), may be written as follows
(Hauptman, 1976)
P( 4|B) = exp(B cos 4) / 2
I0(B) (6)
This function is similar to P(3|A), except that the value of B
will tend to be much smaller for large structures. The probability distribution
of 4 is dependent on more than the principal vectors that go to
make up B and is more correctly
P(4|B,E12,E13,E14) = exp(-B
cos 4) / 2 I0(Z) (7)
where Z is a function of the seven vectors E(h1) to E14. An important property of the probability expression (7) is that if the cross-vectors are large, then expression (6) holds, but if the cross-vectors are small then expression (7) approximates as
P(4|B,E12,E13,E14) = exp(-B
cos 4) / 2 I0(2B) (8)
The importance of this result may be illustrated for a fixed value of B (for example, 3.) and for small and large cross-vectors (XV)
Because of the dependence of 4 on the magnitude of the
cross-vectors, quartets are usually grouped into two classes according to the
sum of cross-vector magnitudes.
XVsum = |E12|+|E13|+|E14| (9)
If XVsum is greater than a certain threshold (e.g. XSHI), a quartet is referred
to as a positive quartet (because cos4 should be
positive). If it is less than a lower threshold (e.g. XSLO), a quartet is known
as a negative quartet (because cos4 should be negative).
GENSIN estimates the value of XVSUM and various procedures can be adopted by
the user to control the generation of quartets using this sum.
4.26.2. Application Of Group Structure Factors
The normalization program, GENEV, converts known structural information into one or more group structure factors G(h) for each reflection. These group structure factors are used in GENEV to calculate an expectation value for F2(h) where M depends on the number of molecular fragments and the nature of the fragment information (see GENEV for details).
<F2(h)> = M G2(h)
(10)
GENEV outputs the group structure factor values as the magnitude G(h) and the
phase g(h). Knowledge of the structure influences the values expected for
. If the atomic parameters are known to a certain precision, then G(h) and
g(h) values (which in this instance are the same as F(h) and (h)) may be
used to predict to the same precision. The group structure factor is in
fact an important component in the conditional probability expressions for
3 and 4.
4.26.2.1. Triplets
Main (1976) modifies the value of A to the form:
A' = 2a' |E(h1) E(h2) E(h3)| (11)
where
a' = MG(h1,h2,h3) /
[<F2(h1)><F2(h2)><F2(h3)>]1/2 (12)
The correspondence between a' and a in expression (3) is quite
apparent when the only knowledge of a structure is its atomic content. Then
each <F2(h)>= f2(s); each
G(h1,h2,h3) = f3(s) and a'
= a. With increasing structural information the value of a' may
differ substantially from a. The most important term in expression (12)
is the joint group structure factor
G(h1,h2,h3) which is calculated directly for
each invariant from the known structural information (see Main, 1976). This
calculation is, however, a time-consuming task even for small structures. A
more efficient approach involving a minimal loss in precision is the use of the
individual group structure factors of the form (Hall, 1978):
a'= M [G(h1) G(h2)
G(h3)] / [<F2(h1)><
F2(h2)><F2(h3)>]
1/2 (13)
4.26.2.2. Quartets
This approximation applied to quartet relationships gives
B' = 2b' |E(h1) E(h2) E(h3) E(h4)| (14)
| M [G(h1) G(h2)
G(h3)G(h4)] | ||
| where b' = | ---------------------------------- | (15) |
| [<F2(h1)><F2(h2)><F2(h3)><F2(h4)> ]1/2 |
In this way fragment information is used to predict the distribution of
3 and 4 according to
P(3|A')
and P(3|B',XVsum).
Most importantly, however, the probability
terms A' and B' from (13) and (14) are complex
A' = |A'| exp(i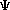 
3 ) and
B' = |B'| exp(i 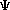4 ) (17)
with the phase values 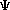3 and 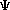4, which are
estimates of 3 and 4, respectively. The
reliability of 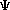3 and 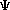4 as phase estimates
depends on the precision of the structural information, and the magnitude of A'
and B', respectively. For random-atom structures (i.e., fragment information
type-1 in GENEV) A' = A and B' = B, and 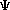3 = 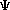4 =
0. If random-fragment (type-2) information is used in GENEV, the
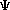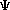3 and 4 values are also assumed to be zero
(this is a limitation of using approximation (15) instead of (14)). For type-3
and type-4 fragments information the values of 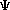3 and
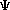4 may be non-zero. In the following description and input line
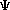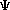formats 3 and 4 values are referred to as the
fragment estimates "QPSI".
4.26.3. Origin And Enantiomorph Definition
In addition to generating structure invariants, GENSIN provides the conditions for the origin and enantiomorph definition of the cell. Fixing the origin and enantiomorph is a necessary first step in the GENTAN phase extension process. It is performed automatically; the user may, however, override this procedure using phases selected according to the definitions output by GENSIN. The conditions for specifying the origin in terms of structure factor seminvariant phases is detailed by Hauptman and Karle (1956) and Karle and Hauptman (1956). Application procedures for applying these conditions are described by Stewart and Hall (1971), Luger (1980), and Hall (1983).
It should be noted that for GENSIN and GENTAN the seminvariant vector conditions are always in terms of the input indices. It is therefore unnecessary to transform centred indices to primitive indices for the purposes of origin specification. Details of the seminvariants vectors for centred space groups are described by Hall (1982).
The origin of a cell is fixed by specifying the structure factor phases of p linearly-independent reflections. The value of p ranges from 0 to 3, and is determined by the space group symmetry.
Any reciprocal lattice vector h is a linear combination of p origin defining vectors h(1). . . h(p)
h = p nj hj (18)
where nj is any integer value. This relationship may be expressed as the vector transformation
h = n H (19)
where n is the set of integers n(1), . . .n(p) and H is the set or origin defining reflections h(1), . . . h(p). The linear relationship of a reflection h to the set of origin defining reflections H is given by
n = h H-1 (20)
A reflection vector h may also be transformed into the seminvariant indices u by the operations
u = h' (mod m) = (u,v,w) (21)
and h' = V h (22)
where V is the seminvariant vector matrix and m the seminvariant moduli (Hauptman and Karle, 1956). A necessary requirement of any set of origin defining reflections is that the matrix of seminvariant indices U
U = (u1, u2,. . . . . up) (23)
has the magnitude
|U| = +1 or -1. (24)
The linear relationship of any structure factor phase (h) may be expressed
in terms of the u from (21) as:
n' = u U-1. (25)
If Q is defined as the set of origin defining phases
Q = ((h1), (h2), . . . .(hp)) (26)
The seminvariant phase due to linear relationship of h to H may be derived from the linear combination of these phases (Hauptman and Karle, 1956)
q(h) = n' Q. (27)
If seminvariant phase q(h) is equal, modulus , to the phase of
vector h, then the value of (h) is independent of the
enantiomorphous structure. If q(h) is significantly different (modulus
) to (h), then the enantiomorph may be specified by fixing
(h) at one of its two possible values.
For space groups where (h) is restricted to one of two values (e.g.
for P212121 (uu0) = ±/2 and
(gu0) = 0,), the calculation of q(h) from integer set n'
and its application to the phase set Q provides a straightforward
approach to identifying the formal requirements of enantiomorphic
discrimination (Hall, 1983).
If all restricted phases have values of (h) = q(h), then a
reflection with a non-restricted phase value must be used to specify the
enantiomorph. For these space groups, q(h) indicates the range of values
(h) should have to separate satisfactorily the enantiomorphs. Typically a
(h) value would be permuted in a multisolution process, to a series
of values for q(h)+/4 to q(h)+3/4 in increments of
/4. Differences between (h) and q(h) of less than /6
will not provide strong enantiomorphic discrimination and are likely to lead to
instability in the phasing process. For examples of enantiomorphic
discrimination see Hall (1983).
4.26.4. Notes On GENSIN Parameters
4.26.4.1. Number of Invariants
In the default mode GENSIN generates both triplet and quartet structure invariant relationships. Invariant types may be specified by the user with the trip and quar control lines. The number of structure invariants generated is determined by a range of parameters, including the number of generators, the magnitude of the E values, and the magnitude of the A and B thresholds. In default mode, the maximum number of invariants for either type is set at 2000.
4.26.4.2. Number of Generators
The reflections used in the generation process are selected from the largest En, where n designates the E-type (1 or 2) output by GENEV. The default value of n is 1. The number of generators is controlled by the user via the gener line, or set automatically according to the algorithm
MAXGEN = max (10000, 150 + NNHA*(4 + ICNT + 1/NEQP)),
where ICNT=1 if centrosymmetric and ICNT=0 if noncentrosymmetric, NNHA is the number of non-hydrogen atoms in the molecule, and NEQP is the number of general equivalent positions.
4.26.4.3. Psi(0) Triplets
Triplet invariants are always generated for up to 100 of the smallest E-values
independent of the TRIP parameters. These are used subsequently in the
(zero) figure-of-merit tests in GENTAN, and are referred to as (0)
triplets (Cochran and Douglas, 1957).
4.26.4.4. Estimation of Psi From bdf Phases
GENSIN provides, via the psical line, the facility to calculate
from phases and structure factor values stored on the bdf. The and
|F| values on the bdf may be from a previous GENTAN run, an FC calculation on a
partial structure, or the back transform of modified density for protein
structures. The bdf lrrefl: ID numbers for and F are assumed to be n750 and n751
unless otherwise specified on the psical line.
4.26.4.5. Application of Fragment QPSI
The inclusion of fragment QPSI values (see the GENSIN line and description above) in the invariant generation process will modify the calculated A and G values, and therefore change the number and nature of invariants generated. This is quite independent of the E used (i.e., E1 or E2). It is recommended that E1, based on random-atom expectation values, are always used, except in special circumstances (see Subramanian and Hall, 1982; Hall and Subramanian, 1982a,b). This is because the QPSI values contain the group structure phase information of the fragment, and E1 has been shown to provide more reliable structure invariant relationships. As a rule-of-thumb E2 should be treated as a second option that the user can invoke in cases of severe non-randomness (e.g., hypersymmetry, super-structures or very dominant heavy atoms).
4.26.4.6. Adjusting |E| Values
The change control line is available for modifying the
magnitude of specific E or 
(E) values. change can be
used to enhance or to suppress a particular E in the generation process by
increasing or decreasing its E value. It is also useful for running "replica"
tests against other software and different machines. Please note that
change lines must be entered in the order of reflection data on
the input bdf, and be the last control lines entered.
4.26.4.7. Types of Quartet Invariants
The nature of quartet invariants generated by GENSIN is determined largely by the cross-vector magnitudes. The types and magnitudes of cross-vectors permitted during the generation process are controlled via the parameters IXVF, XVMN, XVMX, XSLO, and XSHI on the quar line. The XSLO and XSHI parameters apply only to quartets with cross-vectors inside the data sphere. The cross-vector limits XVMN and XVMX are applied to individual cross-vector E values. If an individual cross-vector E lies outside the range XVMN to XVMX the quartet is rejected. In the default mode, the sum of the cross-vector magnitudes XVsum (eqn (9)) is calculated for all cross-vectors inside the data sphere with XVsum < XSLO and XVsum > XSHI.
Quartets generated by GENSIN are used in several different ways in the
subsequent calculations. Typically quartets are divided into three categories:
those with cross-vector sums above an upper threshold XSHI (known as positive
quartets), those below a lower threshold XSLO (known as negative quartets), and
those in between. The last category is often not used in the phasing process
because of the unpredictability of the 4 values. The user can
specify these upper and lower thresholds, XSHI and XSLO, with the
quar line for both the GENSIN and GENTAN calculations.
It is usual to use only quartets with cross-vectors inside the data sphere. The
XVsum is then able to be calculated and a prediction made about the value of
4. There are, however, some drawbacks to this approach. When
XVsum is greater than XSHI it is probable that the quartet generated will in
fact be equivalent to a combination of three triplet invariants also generated
by the GENSIN process. The phase relationships provided by positive quartets
tend therefore to reinforce, rather than add to, those provided by the
triplets. The phase "pathways" provided by quartets will, of course, be
different to those of triplets but the generators they connect will, in effect,
be the same.
Quartets with XSLO < XVsum < XSHI are usually not redundant to triplets but are less useful for the reasons already discussed.
Negative quartets with XVSUM less than XSLO provide completely different phase information to triplets but are very few in number. For this reason they are used in GENTAN for a figure-of-merit parameter.
In contrast, quartet invariants with one or more cross-vectors outside the data
sphere, provide relationships that cannot be represented by a combination of
triplets. These quartets provide new phase pathways and, as such, could prove
crucial in particularly difficult solutions. The disadvantage of these
"extra-terrestrial" quartets is the lack of cross-vector information and,
therefore, the inability to predict the value of 4. However, it
may be assumed that 4 for these quartets has a distribution
based on B (just as 3 is a function of A) and an overall
reliability comparable to that of triplets (ignoring the relative magnitudes of
A and B). See Examples 3 and 4.
4.26.5. File Assignments
Reads E values from the input archive bdf
Writes structure invariant relationships to the file inv
4.26.6. Examples
Generate triplet and quartet invariants to a maximum of 2000 using type-1 E values. Only quartets with cross-vectors inside the data sphere will be output. QPSI values will be applied if fragment information is on the input bdf. Print invariant totals for all generators.
GENSIN nqpi :do not use QPSI information gener *2 300 :use top 300 E values trip yes 1.5 3000 :set max A and max triplets quar no :do not generate quartets print *2 1 50 100 :print SI for gens 1-50 to N of 100 |
Generate maximum of 3000 triplets with A values greater than 1.5 from 300 generators. Available QPSI values are not applied. Structure invariants for the top 50 generators are printed provided all generator numbers are <= 100.
GENSIN smax .45 :exclude all s values >.45 quar yes 0.75 *8 1. 5. :for Q4 B>.75 and XVsum>5 or <1. change 1 7 3 3.2 :make E = 3.2 change 2 3 -4 2.75 :make E = 2.75 |
Generate triplets and quartets for generators selected from Es with s<.45. Quartets will be accepted if B>.75 and has a cross-vector sum (all cross-vectors inside the data sphere) 5. or 1. The E value of reflections 1, 7, 3 and 2, 3, -4 will be modified on input.
Generate triplets and quartets. The quartets must have at least one of their three cross-vectors outside the data sphere.
Generate triplets and quartets. The quartets must have all three cross-vectors outside the data sphere.
4.26.7. References
Cochran, W. and Douglas, D. 1957. The Use of a High-speed Digital Computer for the Direct Determination of Crystal Structures . Proc. Roy. Soc. A243, 281.
Hall, S.R. 1981. A Procedure for Random-access to Reflection Data. J. Appl. Cryst. 14, 214-215.
Hall, S.R. 1982. Seminvariant Vectors for Centred Space Groups . Acta Cryst. A38, 874-875.
Hall, S.R. 1983. A Procedure for Identifying Enantiomorph-Defining PhasesActa Cryst. A39, 22-26.
Hall, S.R. and Subramanian, V. 1982a. Normalized Structure Factors. II. Estimating a Reliable Value of B . Acta. Cryst. A38, 590-598.
Hall S.R. and Subramanian, V. 1982b. Normalized Structure Factors. III. Estimation of Errors . Acta Cryst. A38, 598-608.
Hauptman, H. 1976. Some Recent Advances in the Probabilistic Theory of the Structure Invariants. Crystallographic Computing Techniques. F.R. Ahmed, K. Huml, B. Sedlacek, eds., Munksgaard. Copenhagen: 129-130.
Hauptman, H. and Karle, J. 1956. Structure Invariants and Seminvariants for Noncentrosymmetric Space Groups. Acta. Cryst. 9, 45-55.
Karle, J. and Hauptman, H. 1956. Theory of Phase Determination for the Four Types of Non-centrosymmetric Space Groups 1P222, 2P222, 3P12, 3P22. Acta. Cryst. 9, 635-654.
Luger, P. 1980. Modern X-ray Analysis on Single Crystals. de Gruter: New York.
Main, P. 1976. Recent Developments in the MULTAN System - The Use of Molecular Structure. Crystallographic Computing Techniques F. R. Ahmed, K. Huml, B. Sedlacek, eds., Munksgaard. Copenhagen: 97-105.
Stewart, R.F. and Hall, S.R. 1971. X-ray Diffraction . Determination of Organic Structures by Physical Methods. F.C. Nachod and J.J. Zuckerman, eds., Academic Press: New York, 74-132.
Subramanian, V. and Hall, S.R. 1982. Normalized Structure Factors. I. Choice of Scaling Function. Acta. Cryst. A38, 577-590.