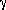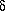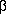4.19. CRYLSQ: Structure factor least-squares refinement
Author: Roeli Olthof-Hazekamp, Laboratorium voor Algemene Chemie, Padualaan 8, 3508 TB Utrecht, The Netherlands
CRYLSQ is a general purpose atomic parameter refinement program. The program can be used for any space group and any setting. It adjusts the scale, extinction, positional, thermal displacement, and site occupancy factors by minimizing the difference between observed and calculated structure factors. Refinement may be based on F, F2 or I. Provision is made for the control of parameters of atoms in special positions; and the refinement of rigid groups or identical molecules; refinement of the Flack absolute structure parameter XABS; and restraints involving bond distances, angles and dihedral angles. Derivatives are accumulated as full matrix, blocked matrix, or diagonal matrix at the user's discretion.
4.19.1. Calculations Performed
The following equations give a summary of the method of establishing the least-squares equations which are used in the CRYLSQ program. The user is referred to a standard crystallographic text for the background to these calculations (Buerger, 1960). The methodology follows closely that which has been used by Busing and Levy (1959), among others. The main enhancements are concerned with the automation of the handling of special positions, matrix blocking, rigid groups, and identical molecules.
Least-squares Procedure
In the least squares procedure the function Q is minimized:
Q =  h [w(Yo - Yc)2] =
h [w(Yo - Yc)2] =
 h [w
h [w  2] (summed over all hkl) (1)
2] (summed over all hkl) (1)
where Yo is the 'observed' value of |F| or F2 or I ; Yc is the calculated value of |F| or F2 or I and w is the least squares weight. The calculated structure factor F is:
Fc = Ac + i Bc (2)
Ac =  n [
n [  s {ƒ1 cos
s {ƒ1 cos - ƒ2 sin
- ƒ2 sin } ] (2a)
} ] (2a)
Bc =  n [
n [  s {ƒ1 sin
s {ƒ1 sin + ƒ2 cos
+ ƒ2 cos } ] (2b)
} ] (2b)
where  n is the sum over the atoms;
n is the sum over the atoms;  s is the sum over the
equivalent positions. The structure factor components are:
s is the sum over the
equivalent positions. The structure factor components are:
ƒ1 = (f + f') K M P exp(U) and ƒ2 = f" K M P exp(U);
cos = cos 2
= cos 2 (hx + ky + lz) and sin
(hx + ky + lz) and sin = sin 2
= sin 2 (hx + ky +
lz),
(hx + ky +
lz),
where K is the reciprocal scale factor; M is the multiplicity; P is the population parameter; exp(U) is the thermal displacement term; f is the atomic scattering factor; f' is the real part of dispersion factor and f" is the imaginary part of dispersion factor.
Minimization of Q gives for each parameter pi:
Q/dpi =  r [w
r [w  dYc /
dpi ] = 0 (3)
dYc /
dpi ] = 0 (3)
Since the structure factor is not a linear function of the parameters, the
function must be expanded in a Taylor series:
Yc = Yc(0) +  j [
j [
 j dYc / dpj ] + H (4)
where
j dYc / dpj ] + H (4)
where  j is the sum over the parameters; Yc(0)
is the structure factor calculated from start parameters;
j is the sum over the parameters; Yc(0)
is the structure factor calculated from start parameters;
 j is the
difference between real and start value of parameter pj and H is
the higher order terms (neglected in CRYLSQ).
j is the
difference between real and start value of parameter pj and H is
the higher order terms (neglected in CRYLSQ).
The normal equations are obtained by substituting equation (4) in equation
(3):
 r [ wYo - Yc(0)
-
r [ wYo - Yc(0)
- j
j  j Yc/dpj } dYc/ dpi ] = 0 (5)
which can be written as
j Yc/dpj } dYc/ dpi ] = 0 (5)
which can be written as
 r [ w
r [ w j { dYc/dpi
j { dYc/dpi j dYc/dpj
] =
j dYc/dpj
] =  r [
w
r [
w j { dYc/dpi
j { dYc/dpi  } ](5a)
} ](5a)
 j [ Aij
j [ Aij  j ] = Bi
j ] = Bi (5b)
or in matrix notation
A
(5b)
or in matrix notation
A  = B (5c)
where
= B (5c)
where
Aij =  r [ w dYc/dpi
dYc/dpj ] and
Bi =
r [ w dYc/dpi
dYc/dpj ] and
Bi =  r [ w
dYc/dpi
r [ w
dYc/dpi  ]
]
The formulae of the various derivatives are given in the section on
derivatives. The shifts,  j, are calculated
from this
equation. Because the normal equations are approximated functions, the
calculations do not lead to the true values of the parameters. However, the
shifts can be used to correct the starting values. The new parameters can be
used as starting values in a subsequent refinement cycle.
j, are calculated
from this
equation. Because the normal equations are approximated functions, the
calculations do not lead to the true values of the parameters. However, the
shifts can be used to correct the starting values. The new parameters can be
used as starting values in a subsequent refinement cycle.
4.19.2. General Structure Parameters
4.19.2.1. F relative Scale Factor(s)
F-relative scale factor(s) are refined as reciprocal scale factor(s) SKF. When groups of reflections have different scale factors, these can be refined separately or as a unit.
4.19.2.2. Pseudo-overall Thermal Displacement Parameter
The overall displacement parameter is used to calculate a measure of the correlation between scale factor(s) and displacement parameters. The scale factors and displacement parameters of a structure are always correlated. If they are refined in separate blocks, incorrect shifts will result unless the correlation is taken into account. By refining the pseudo-UOV in the same block as the scale factor, a compensation is made for the correlation. Individual displacement parameters must also be adjusted based upon the shift in the pseudo-UOV. They are corrected with:
BCORR =  (UOV) -
(UOV) -  '(UOV) (6)
'(UOV) (6)
where  (UOV) is the shift obtained from an n by n matrix with SKF and
pseudo-UOV, and
(UOV) is the shift obtained from an n by n matrix with SKF and
pseudo-UOV, and  '(UOV) is the shift obtained from a 1 by 1 matrix with
the pseudo-UOV only. The
'(UOV) is the shift obtained from a 1 by 1 matrix with
the pseudo-UOV only. The  (pseudo-UOV) is not applied to the overall
thermal displacement parameter, when there are no atoms with an overall value
to be refined.
(pseudo-UOV) is not applied to the overall
thermal displacement parameter, when there are no atoms with an overall value
to be refined.
4.19.2.3. Dispersion Parameters
Atomic scattering factor dispersion factors are applied in the calculation of the structure factors when this is requested in the CRYLSQ line by the ad specification. The values are present in logical record lrscat: of the bdf or are given in disper lines. When specified in both ways, the disper line values are used.
Refinement of all dispersion parameters is turned on by rd in the CRYLSQ line. Using noref lines, in combination with rd in the CRYLSQ line, turns off the refinement of the indicated parameters. In the blocked refinement modes, the dispersion factors are refined in the same block as the scale factor(s).
4.19.2.4. Extinction Parameters
Isotropic extinction parameters may be applied or refined in CRYLSQ. The formalism of Zachariasen can be used, employing the expressions of Larson (1970). Zachariasen introduced two crystal types:
Type I extinction is dominated by the mosaic spread (sometimes referred to as secondary extinction). The extinction is parametrised by the refinable quantity g which is related to the mosaic distribution function.
Type II extinction is dominated by the particle size (sometimes referred
to as primary extinction). The correction is parametrised by the
refinable quantity 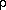 .
.
The correction y applied to each reflection intensity is y = (1 + 2x)-1/2
Details are given in Larson (1970). The above formula does not differentiate
between Type I or II explicitly, although values of g or 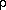 may be inferred
by the user, as explained below.
may be inferred
by the user, as explained below.
For more severe secondary extinction and for primary extinction the formalism
of Becker and Coppens (1974a) may also be used. The Becker-Coppens expression
for y involves a higher order expansion given by
where i=s (secondary) or i=p (primary). The expressions for ai,
bi and ci for primary extinction and for secondary
extinction using either Gaussian or Lorentzian distributions are given in
Becker and Coppens (1974a). Type I or II may be refined in that formalism. A
third type denoted General which represents a mixture of the two types is a
further option in which both g and 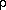 are refined simultaneously.
Their high correlation often leads to convergence problems.
are refined simultaneously.
Their high correlation often leads to convergence problems.
For Type II and General, primary extinction is refined simultaneously since any secondary extinction affected by particle size will have some primary component and be dependent on it. For neutron diffraction the total extinction correction y is
y = yp(xp) . ys (yp(xp) . xs)
The expression in the x-ray case is functionally similar but includes polarisation terms due to the specimen and the monochromator crystal, as given by Becker and Coppens (1974b) in an appendix.
The primary (type II) extinction variables are:
The secondary (type I) extinction varaiables are: where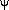 = g /sin 2 = g /sin 2 | for TYP1 |
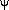 = = 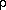 | for TYP2 |
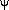 = = 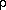 /(1+( /(1+(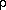 sin2 sin2 /g)2)1/2 /g)2)1/2 | for GEN with a Gaussian distribution |
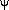 = = 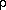 /(1+ /(1+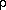 sin 2 sin 2 /g) /g) | for GEN with a Lorentzian distribution |
These expressions indicate the strong dependence of the extinction correction
on Fc. For given g or 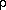 , different values of y can be obtained
depending on the structure factor model. This is a consequence of the
Zachariasen or Becker and Coppens formalism for the posteriori
correction of intensities for extinction.
, different values of y can be obtained
depending on the structure factor model. This is a consequence of the
Zachariasen or Becker and Coppens formalism for the posteriori
correction of intensities for extinction.
For the Zachariasen correction, r* is equal to the final value of EXT printed
by CRYLSQ multiplied by 104. That is, if EXT=.2 then r*=
2000. If one assumes that the extinction is Type I then r* = g. If one assumes
a Type II extinction then r* = 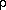 .
.
The values of g and 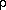 obtained are dimensionless and relate
to the physical properties of the crystal in the following manner,
obtained are dimensionless and relate
to the physical properties of the crystal in the following manner,
 1/2 = (ln 2 / 2 1/2 = (ln 2 / 2 )1/2 / g radians )1/2 / g radians | (= .33214 /EXTx104) for the Gaussian distribution |
 1/2 = 1 / (2 1/2 = 1 / (2 g) radians g) radians | (=.15915/EXTx104) for the Lorentzian distribution, where the half width  1/2 of the distribution indicates the mosaic spread 1/2 of the distribution indicates the mosaic spread |
r = 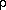 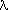 | (= RHO x 104 x 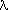 ) where r is thesize of the mosaic blocks and ) where r is thesize of the mosaic blocks and 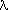 the wavelength the wavelength |
4.19.2.5. Absolute-Structure Parameter
The absolute-structure (twin) parameter xabs may be used to define the absolute configuration or polarity of untwinned crystals (Flack, 1983). The crystal is described as an inversion twin. 1-x and x are the fractions of the structure and its inverse in the macroscopic sample. The structure factor equation is given by
|F(h,k,l,xabs)|2 = (1-x) |F(h,k,l)| 2 + x |F(-h,-k,-l)|2
xabs converges in 2 to 4 cycles, depending on the anomalous dispersion contribution, to values between 0. and 1., within 3 e.s.d.'s. Friedel pair measurements must be present in the bdf for all or part of the reflections. Note that the pakfrl option needs to be used in SORTRF to pack pairs into a single packet.
4.19.3. Atom Specific Parameters
4.19.3.1. Positional Parameters
All positional parameters for selected atoms are refined unless a noref condition is present to direct that a parameter be held invariant.
4.19.3.2. Thermal Displacement Parameters
The program can be used to refine the values of overall, isotropic, anisotropic or mixed thermal displacement parameters. In the mixed mode these parameters are set in accordance with the specification stored in the bdf. For one or more atom types the mode can be changed by the use of a dptype line. In the program, use is made of u or uij. On the printed output, U values (multiplied by 100) are displayed. After correction, the displacement parameters are tested to be sure of their physical significance. If an isotropic thermal displacement parameter is negative or an anisotropic displacement tensor is not positive definite, a warning is printed. When a displacement parameter is found to be non-positive definite one of three options can be specified in the CRYLSQ line -- continue with calculated values ( tw ), reset displacement to positive definite and continue ( tr ), or stop ( tt ).
4.19.3.3. Treatment of Atoms With uov
When one or more atoms has an overall thermal displacement parameter and the use of a full matrix is specified, derivatives are calculated with the formulae that is used for the uov, but summation is over only those atoms with uov. When other block types are used, the summation for UOV is over all atoms.
4.19.3.4. Population Parameter
The term population parameter is used to describe the occupancy of an atom site. It is independent of atom multiplicity for the site. Population parameters are applied in the calculation only when they are present in logical record lratom: of the bdf. Their refinement flag is turned on by the pp code in the CRYLSQ line. noref lines can be used to turn off refinement of indicated population parameters.
4.19.4. Solution Of The Normal Equations
The normal equations are solved by the method of Choleski. A is a positive definite, symmetric matrix. It is decomposed to an upper triangle U and a lower triangle L. Matrix L is the transpose of U, so only enough memory to hold half the matrix is required.
A  = L U
= L U  = B
(7)
= B
(7)
From the decomposed triangle U the shifts can be calculated easily.
4.19.5. Estimated Standard Deviations
The estimated standard deviations are derived by the following expression where n is the number of reflections and m is the number of variables:
 i = {Aii-1
i = {Aii-1  r
[w
r
[w  2]/(n - m)}1/2 (8)
2]/(n - m)}1/2 (8)
For the calculation of standard deviations, the inverted matrix is required. It is obtained by inverting the triangular matrix. Because the inversion is a rather time consuming, the standard deviations are calculated only during the last cycle.
4.19.6. Blocking
There are several options for blocking the matrix of normal equations, A.
All parameters may be refined in one block. This is referred to as full matrix and is specified by fm in the CRYLSQ line.
The matrix may be blocked so that there is one block for the parameters of each atom. This is referred to as block diagonal and is specified by bd in the CRYLSQ line.
The matrix may be blocked in such a way that each block contains the parameters for more than one atom. The option is specified by bl in the CRYLSQ line. When this specification is made details of the structure of the blocks must be given in block lines.
The matrix may be divided into blocks containing any arbitrary parameters. This option is indicated by bl in the CRYLSQ line. Details of the structure of the blocks must be given in block lines.
4.19.7. Invariant Parameters
Parameters can be held invariant by two methods:
4.19.7.1. Method 1:
By commands from logical record lrcons: of the bdf. These commands are generated by the program ADDATM and specify atoms in special position. See the documentation on ADDATM for details.
4.19.7.2. Method 2:
By a noref line. The general form for the invariant parameter set is:
| (P1/P2)(R1/R2) or (P1,P2)(R1,R2) or any combination of these | |
| P1/P2 parameter symbols P1 to P2 inclusive (see lists below) | |
| P1,P2 parameters P1 and P2 only | |
| R1/R2 atom name's R1 to R2 inclusive | |
| R1,R2 atom name's R1 and R2 only |
If only an atom name or atom type is present, then all the parameters for that atom or atom type are held invariant. If only a parameter is specified, then that parameter is held invariant for all atoms. More than one invariant parameter set may be input on a noref line. In addition to the individual atom parameters the following general parameters may also be specified invariant:
| skf | scale factor(s) |
| uov | overall thermal displacement parameter |
| ext | extinction parameter(s) |
| dsp | dispersion factors |
There exist atom types Y and U. In these cases, parameter symbols and atom types must be present.
noref y(c3) : y invariant for atom c3 noref (x,z)(c2,c5) : x and z invariant for atoms c2 and c5 noref (x/u11)(c1/c3) : x to u11 invariant from atom c1 to c3 noref u : u invariant for all atoms noref c5 : all parameters invariant for atom c5 noref u(h) c : u for h atoms and all c parameters invariant |
4.19.8. Dependent Parameters
Parameters may be constrained to be relative to other parameters by: the space group symmetry requirements of an atom sited at a special position, the requirements of definition of the origin in polar space groups or use of the constr option as specified by the user. ADDATM will detect atom parameters constrained by space group symmetry or polar space group requirements and store the information in logical record lrcons: of the bdf.
The general form of a constraint equation on the constr line is:
par(s)(atom(s)) = Q + fct(1)*par(1)(atom(1)) +...+ fct(n)*par(n)(atom(n))
where
| par(s) | = subject (dependent) parameter |
| atom(s) | = subject (dependent) atom name |
| Q | = constant term |
| par(1,2,..,n) | = reference (independent) parameter(s) |
| atom(1,2,..,n) | = reference (independent) atom name(s) |
| fct(j) | = multiplication factor for corresponding parameter par(j) |
Note that the subject parameter or atom must not precede the reference parameter or atom in the parameter or atom list. That is,
| y(Cu1)=0.0+2.0*x(Cu1) | is correct |
| x(Cu1)=0.0+0.5*y(Cu1) | is not correct |
| x(Cu2)=0.5+1.0*x(Cu1) | is correct |
| x(Cu1)=0.5+1.0*x(Cu2) | is not correct |
Two examples follow:
Though the first example is unlikely it illustrates the general form of a constr line input. The use of the constr line restricts the value of the x parameter of the atom C1 to be equal to the y parameter of O2 minus half of the z parameter of C3 plus a constant term. The second example is common in mineral structures where stoichiometric disorder occurs at atom sites. The total population of the two atom types at the site must sum to a population of one.
If the input parameters do not satisfy the above equation prior to refinement, they are modified to do so, except when the constant value Q is given as the letter Q. The applied shifts always satisfy the constraint equation.
4.19.8.1. Mathematical Treatment of the Dependent Parameters
In polar space groups the position of the origin in one or more directions is not fixed by symmetry elements. Coordinates in a polar direction can be considered as a special case of constraints. One polar coordinate depends on all others.(The factors are negative 1.) In the block diagonal approximation polarity does not have to be considered, because it will not lead to singularity of the matrices.
The contribution of the dependent parameters to the derivatives of the
reference parameters is expressed in the chain rule where sum(i) is the sum
over all parameters dependent on p(j), including the derivative of p(j) itself
(Finger, 1969).
dF/dpj =
 i [fct(i) dF/dpi] (9)
i [fct(i) dF/dpi] (9)
The standard deviation of the dependent parameter is calculated according to
the approximate formula:
 pi = {
pi = { j
[
j
[  k [fct(j) fct(k) COV(j,k) ] ]
k [fct(j) fct(k) COV(j,k) ] ]
 r [w
r [w 2]/(n-m) }1/2 (10)
2]/(n-m) }1/2 (10)
where COV(j,k) is the covariance of the jth and kth reference parameters.
4.19.9. Rigid Groups And Identical Molecules
The total number of parameters in a structure can be reduced if some subset of the atoms can be considered as a rigid group. Idealized coordinates for rigid groups can be calculated and written to the bdf either by the program RIGBOD or by the program BONDAT. Another method of reducing the total number of parameters is when a structure contains two or more fragments consisting of "identical" points. These are referred to as identical molecules. Using the identical molecule, two or more groups of atoms in a crystal structure can be forced to maintain the same intermolecular structure during the refinement.
In both cases use is made of the Euler parameters: three coordinates of the centre of gravity and three angles that relate the principal axes of the group to the cell axes respectively, to the principal axes of the first identical molecule. For the Euler angles the Goldstein definition from classical mechanics is used. The calculation of the principal axes is accomplished by the diagonalization of the inertia tensor by the method of Jacobi.
For a non-degenerate inertia tensor three non-collinear atoms are needed in the rigid group. Groups positioned on a symmetry element lead to dependent or invariant Euler parameters. Information on fixed parameters must be given in the group line; dependency must be given in constr lines for the first atom(s) of the group(s).
Thermal displacement parameters and population parameters can be refined either for the individual atoms or for the groups (for group isotropic displacement parameters only). Dependencies of these parameters for different groups can be maintained by the use of constr lines. When there is only one displacement parameter or one population parameter for a group, one constr line will suffice (for the first atoms of the groups).
4.19.10. Restrained Parameters
The use of stereochemical data as individual observational equations was first proposed by Waser (1963). In CRYLSQ these eqquations are referred to as restraints. The atom model is restricted to a realistic range of geometries. The weights are inversely related to the standard deviation of the distribution of possible values. The extra term to be minimized by the least squares process is
 n wn (
n wn ( n -
n -  nobs)2
nobs)2
where  n is either the bond distance,
bond angle, or dihedral angle; and
n is either the bond distance,
bond angle, or dihedral angle; and
wn =  r [w
r [w  2] / (n-m) * 1 /
2] / (n-m) * 1 / 2
2 n
n
4.19.11. Weighting
The process of refinement of a crystal structure utilizing a nonlinear least-squares procedure requires some attention to be given to the weight assigned to each experimental observation. In the XTAL system, the quantity stored in the binary data file is the square root of the reflection weight (this convention has arisen because it saves many thousands of multiplication operations during the building of the matrix and vector of the normal equations). The practice follows that established in ORXLS (Busing and Levy, 1959) and is common to many least squares programs.
The derivation of the values of the weights is a matter of considerable
controversy in the crystallographic literature. For this reason, a number of
methods of dealing with the problem of establishing values suitable to the user
are provided. The weights to be applied may be specified in three different
ways: a weight of 1.0 for all observations ( wu ), a weight of
1/ 2F ( ws ), or the weights supplied in the bdf
( ww ).
2F ( ws ), or the weights supplied in the bdf
( ww ).
4.19.12. Partial Shift Factor
In all block modes a partial shift factor of 0.8 is automatically applied. The factor may be changed by using the code fu q in the CRYLSQ line. The factor which is used will depend on the correlation between atoms in different blocks. When correlations are high, a small shift factor should be applied to damp the shifts.
4.19.13. Reflection Classification
Poorly measured data points can be treated in a number of ways. A broad
category, referred to as less-thans (rcode=2) may be suppressed from the data
set by the tl q option in the CRYLSQ line where
the threshold of observability is defined in terms of multiples of  (F,
F2, or I).
(F,
F2, or I).
In general, less-thans are not contributed to the least-squares matrix. This
can be overridden by the ml option on the
CRYLSQ line which forces all less-thans with a Fc
greater than Fo to contribute to the matrix. Only those reflections
considered to be more accurately measured (where the weight* (F) is less
than some user defined quantity q ) can contribute to the matrix
by the mr q option in the CRYLSQ line. When
this reclassification is specified, it is only applied during the current
calculation. It will not be written to the bdf.
(F) is less
than some user defined quantity q ) can contribute to the matrix
by the mr q option in the CRYLSQ line. When
this reclassification is specified, it is only applied during the current
calculation. It will not be written to the bdf.
4.19.14. Scattering Factors
Scattering factors are entered from the bdf. If interpolated scattering factors are present on the reflection data record lrrefl: (as inserted by ADDREF), these will be used. Otherwise, scattering factors are extracted from the form factor tables on lrscat:.
WARNING:The scattering factors from the form factor tables are considered sufficiently reliable for routine analyses with R-factors above 0.03. For more accurate analyses the interpolated form factors must be used.
4.19.15. Space Group Symmetry
The CRYLSQ program is general with respect to symmetry. The symmetry operations stored in the bdf are used to generate all the symmetrically equivalent points for the asymmetric set of reflections and atoms supplied. It is important to note that there must be no systematically absent reflections coded as observed reflections (rcode=1 or 2) included in the data supplied.
4.19.16. Fixed Atom Contribution
The number of unique atoms which is used for the calculations may be limited. The structure factor calculation and refinement procedure can be carried out with a selected set of atoms (use the select line). Fixed contributions to the structure factors for the remaining atoms must have been calculated in a former structure factor calculation with FC or CRYLSQ. By using ep in the CRYLSQ line the fixed contributions ar applied as partial contributions too the structure factor sums and they are stored in lrrefl: (IDN 1810 etc.). In subsequent runs, with the same selected atom set, the same fixed contributions may again be applied ( ap in the CRYSLQ line). In this way it is possible to carry out blocks of refinements of various parts of the structure to achieve overall refinement of the complete structure.
4.19.17. Initial Refinement
During the initial steps of refinement it is not always necessary to use all reflections. The number of reflections can be limited by:
Defining a sin
 /
/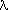 range in a maxhkl line.
range in a maxhkl line.Assignation of maximum h, k and l values in a maxhklline.
Skipping of reflections with the sk n option in the CRYLSQ line.
4.19.18. Derivatives
The following formulae give the equations used in the calculation of the derivatives of F(cal) required in the building of the least-squares matrices.
The structure factor equation (2) can be written as:
F =  n [(A/F)(A' - B") + (B/F)(B' + A")] =
n [(A/F)(A' - B") + (B/F)(B' + A")] =
 nFnb
nFnb
where A' =  s [f1 cos
s [f1 cos  ]
B' =
]
B' =  s [f1 sin
s [f1 sin  ]
]
and A" =  s [ƒ2 cos
s [ƒ2 cos ]
B" =
]
B" =  s [ƒ2 sin
s [ƒ2 sin ]
]
The factors A/F and B/F are introduced to relate the phases of the partial derivatives with the phase of F. The formulae for the derivatives are:
4.19.18.2. Overall thermal displacement parameter (uov)
dF/dUOV = -s2  n'Fn'
n'Fn'
where n' is the atoms with overall thermal displacement parameter. When uov is used for the correlation correction, the summation is over all atoms.
4.19.18.3. Dispersion factors (f' and f")
dF/df' =  n' [ƒ1 /(f+f') ((A/F)A' + (B/F)B')]
n' [ƒ1 /(f+f') ((A/F)A' + (B/F)B')]
dF/df" =  n' [ƒ2 / f'' ((-A/F)B" + (B/F)A")]
n' [ƒ2 / f'' ((-A/F)B" + (B/F)A")]
where n' is the atoms with specified f' and f''.
4.19.18.4. Extinction factors
dF/dg = -.5*DELT*F3*(1+2*g*DELT*(F2))-5/4
where the derivatives are reported by Becker & Coppens (1974).
4.19.19. File Assignments
Reads atom and reflection data the input archive bdf
Writes refined atom and reflection data the output bdf
Optionally writes correlation matrix to file cmx
Optionally outputs atom lines to the line file PCH
4.19.20. Examples
The input above causes all the defaults to be taken by CRYLSQ. All positional and thermal parameters of all atoms on the bdf will be refined in a single cycle of block diagonal refinement based on F(rel). The thermal displacement parameter type used in the calculation for each atom will be read from logical record lratom: of the bdf.
The compound used in this example is 4,4'-dinitrodiphenyl.The bdf for this example has been formed so that the first atom in lratom: is N1. It is followed by O1, O2 and carbon atoms C11 through C16. After these atoms comes N2 and then the remaining atoms. The block line requests that the matrix be blocked in two pieces, each block containing the atoms of one of the rings. Such a blocking scheme can be useful at early stages of refinement or when there is insufficient storage to hold the entire matrix. The information on the CRYLSQ line specifies three cycles of refinement on F2 with isotropic thermal displacement parameters for all atoms.
Both parts of the molecule are refined as rigid groups. There is only one isotropic thermal displacement parameter for all 18 atoms.
ADDREF dset 1 extf reduce f2tof rlp2 neut hklin hkl f2rl sgf2 hkl 0 0 2 5.227 1.303 hkl 0 0 4 19.679 2.195 |
CRYLSQ asn nu f2 ws rx cy 3 fm scale 0.2295 1 extinc *4 .11726 noref C1/H10 CRYLSQ asn nu f2 ws l1 cy 2 fm rx |
4.19.21. References
Becker, P.J. and Coppens, P. 1974. Extinction within the Limit of Validity of the Darwin Transfer Equations. I. Refinement of Extinction in Spherical Crystals of SrF2 and LiF. Acta Cryst. A30, 148.
Buerger, M.J. 1960. Crystal Structure Analysis. New York: John Wiley.
Busing, W.R. and Levy, H.A. 1959. ORXLS, A Crystallographic Least-squares Refinement Program for the IBM 704. ORNL Report ORNL-CF 59-4-37
Finger, L.W. 1969. The Inclusion of Secondary Extinction in Least-Squares Refinement of Single-crystal X-ray Data. Yearbook 67. Carnegie Inst.Washington: 216.
Flack, H.D. 1983. On Enantiomorph-Polarity Estimation. Acta Cryst.A39, 876.
Larson , A.C. 1969. The Inclusion of Secondary Extinction in Least-Squares Refinement of Crystal Structures. Crystallographic Computing. F.R. Ahmed, S.R.Hall, C.P. Huber, eds., Munksgaard. Copenhagen: 291-294.
Waser, J. 1963. Least-Squares Refinements with Subsidiary Conditions. Acta Cryst. 15, 1091.
Zachariasen, W.H. 1967. A General Theory of X-Ray Diffraction in Crystals. Acta Cryst. 23, 558.