4.29. LATCON: Refine lattice parameters
Authors: Dieter Schwarzenbach and Geoff King
Contact: Geoff King, Fysica-Chemische Geologie, K.U. Leuven, B-3001 Heverlee, Belgium
LATCON is a rewrite of Dieter Schwarzenbach's program of the same name in
the XRAY76 system. It determines the 'best' lattice parameters and their
standard deviations from the 2 diffraction angles of a set of indexed
reflections, taking into account any constraints imposed by the crystal system
and allowing for systematic errors in the zero values.
diffraction angles of a set of indexed
reflections, taking into account any constraints imposed by the crystal system
and allowing for systematic errors in the zero values.
Given a set of indexed reflections with their diffraction angles 2 , the
program uses the least-squares method to determine the best values of the
reciprocal and direct metric tensors and lattice parameters with their
estimated standard deviations (esd's) together with the variance-covariance and
correlation matrices. The 2
, the
program uses the least-squares method to determine the best values of the
reciprocal and direct metric tensors and lattice parameters with their
estimated standard deviations (esd's) together with the variance-covariance and
correlation matrices. The 2 values may have been obtained by powder or
single-crystal measurements. Different schemes are available for allowing for
systematic errors.
values may have been obtained by powder or
single-crystal measurements. Different schemes are available for allowing for
systematic errors.
In principle there are two methods of refining lattice constants by minimizing
R =  w (2
w (2 obs - 2
obs - 2 calc)2
calc)2
The first is to express 2 as a non-linear function of the lattice
constants. This leads to a non-linear least-squares procedure which requires
starting values and several cycles of refinement. The second, used here, takes
advantage of the fact that sin2
as a non-linear function of the lattice
constants. This leads to a non-linear least-squares procedure which requires
starting values and several cycles of refinement. The second, used here, takes
advantage of the fact that sin2  is a linear function of the
reciprocal metric tensor giving a linear least-squares problem which can be
solved directly without the need for starting values and without iteration. The
much more complicated task consists then in computing the esd's of the best
lattice constants from those of the reciprocal metric tensor elements.
is a linear function of the
reciprocal metric tensor giving a linear least-squares problem which can be
solved directly without the need for starting values and without iteration. The
much more complicated task consists then in computing the esd's of the best
lattice constants from those of the reciprocal metric tensor elements.
The following concepts are useful:
| Metric tensor (M) | Reciprocal metric tensor (M*) | Vector (v*) |
| a2 a.*b a.*c | a*2 a*.*b* a*.*c* | h |
| a.b b2 b.c | a*.b* b2 b*.c* | k |
| a.c b.c c2 | a*.c* b*.c* c2 | l |
All symbols containing a "*" refer to reciprocal space. The matrix M* is the inverse of the matrix M. The vector v*T is the row vector (h k l), i.e. v* transposed. Therefore,
sin2  = (
= (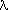 2/4)
(v*T M* v*)
2/4)
(v*T M* v*)
The variance-covariance matrix COV (see e.g. ref. 1) is calculated from the inverse N-1 of the normal-equation matrix N.
COV = eN-1 , e = R/(n-k)
With R defined above, n = number of observations, k = number of parameters
refined, n-k is the number of degrees of freedom and e the variance of an
observation with unit weight, so √e, the error of fit, is the corresponding
 . If the weights are the reciprocals of real variances,
the expectation
value for the error of fit is unity and R should be distributed as
. If the weights are the reciprocals of real variances,
the expectation
value for the error of fit is unity and R should be distributed as
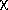 2.
The diagonal terms of COV are the variances whose square
roots are the standard deviations (esd's),
2.
The diagonal terms of COV are the variances whose square
roots are the standard deviations (esd's),  .
The ij th term of the correlation matrix COR is given by
.
The ij th term of the correlation matrix COR is given by
CORij = COVij / ( i
i
 j)
j)
The law of propagation of errors expresses the variance-covariance matrix
COVBof derived quantities b1=
function1(a1, a2,...), b2 =
function2(a1, a2...), etc in terms of COVA of
a1,a2,... Denoting the derivative of bk with
respect to al by
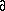 bk/
bk/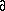 al and the matrix of
derivatives as D, we obtain
al and the matrix of
derivatives as D, we obtain
COVBij =  k,l
k,l
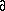 bi/
bi/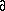 ak
ak 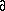 bj/
bj/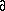 al COVAkl
al COVAkl
COVB= D COVA D T
The program proceeds by the following steps:
The esd's (i.e.
 's) of the 2
's) of the 2 values are used to compute the
values are used to compute the
 's of sin2
's of sin2
i.e. Q = 1/d2 = 4 sin2
 /
/ 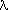 2
2where d is the interplanar spacing. According to the error propagation law,
 (Q) = (2/
(Q) = (2/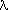 2) sin2
2) sin2
 (2
(2 )
The weight is 1/
)
The weight is 1/ 2.
2.With these weights the linear least squares problem is set up, the symmetry constraints are introduced and the tensor M* is determined together with COV and COR. These matrices are complete and include the elements which are determined by the crystal symmetry and which must not be refined. Thus the variances, covariances and correlations of invariant terms are zero. For a dependent term s = k x t we obtain
variance(s) = k2 variance(t) ;
 (s) = k
(s) = k  (t)
(t)covariance(s,t) = k variance(t) ; correlation(s,t) = 1
The reciprocal lattice constants a*, b*, c*, cos
 *, cos
*, cos 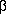 * and
cos
* and
cos 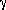 * are determined together with their COV and COR
matrices, using the error propagation law. The
* are determined together with their COV and COR
matrices, using the error propagation law. The  's of these quantities
are again the square roots of the diagonal terms of COR; the
's of these quantities
are again the square roots of the diagonal terms of COR; the  of
the angles in degrees are derived from those of their cosines.
of
the angles in degrees are derived from those of their cosines.The matrix of the reciprocal metric tensor M* is inverted to give M, again with the appropriate COV and COR matrices. This requires the evaluation of all 36 derivatives of the matrix elements with respect to the reciprocal matrix elements e.g.
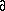 a*b/
a*b/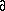 a*2,
a*2, 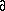 b2/
b2/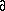 c*2
etc.
c*2
etc.The direct lattice constants are obtained as in step 3. If all reflections have been measured with the same wavelength, the COR matrix and therefore the
 's may be corrected for the uncertainty of the
wavelength,
's may be corrected for the uncertainty of the
wavelength,  (lambda;), which is especially interesting in neutron
diffraction.- This must not, of course, involve the least-squares weighting.
Since the relative error in Q due to an error in the wavelength is
(lambda;), which is especially interesting in neutron
diffraction.- This must not, of course, involve the least-squares weighting.
Since the relative error in Q due to an error in the wavelength is (Q)/Q = 2
(Q)/Q = 2 (
(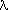 )/
)/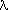
The variances of M* after refinement are increased by
 2(Q) x tensor element. The covariances are derived so as to
leave the correlation coefficients unchanged.
2(Q) x tensor element. The covariances are derived so as to
leave the correlation coefficients unchanged.
4.29.1. Systematic Errors
Two mutually exclusive schemes for taking account of systematic errors may be used in the refinement. Both involve refinement of an additional parameter Dk.
This scheme is included when the mnemonic rq is used in the LATCON line. It has been shown (2) that errors in the measured d-values (
 d) caused by absorption and spherical eccentricity of the
specimen are approximately proporional to
d) caused by absorption and spherical eccentricity of the
specimen are approximately proporional to d = k d cos2
d = k d cos2 = - 2Dk d
cos2
= - 2Dk d
cos2
where d=1/sin
 . Thus
. Thus  Q is equal to the derivative of Q with
respect to d times
Q is equal to the derivative of Q with
respect to d times  d.
d. Q = Dk (4/
Q = Dk (4/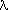 2) sin22
2) sin22
Dk is refined as an additional parameter. The computed Q and 2
 values listed in the output are no longer the TRUE values but they
include the correction term. This correction can be used if the position of the
primary beam is well-known, i.e. if 2
values listed in the output are no longer the TRUE values but they
include the correction term. This correction can be used if the position of the
primary beam is well-known, i.e. if 2 has been determined from
corresponding reflections at plus and minus 2
has been determined from
corresponding reflections at plus and minus 2 or with respect to an
internal standard. Note that many high orders must be included in the
refinement since the error approximation is valid for high scattering angles
and corresponds to an extrapolation of d to cos2
or with respect to an
internal standard. Note that many high orders must be included in the
refinement since the error approximation is valid for high scattering angles
and corresponds to an extrapolation of d to cos2 zero.
Furthermore, the relative error
zero.
Furthermore, the relative error  Q/Q in Q is proportional to
cos2
Q/Q in Q is proportional to
cos2 which has non-negligable values at quite high angles.
Limiting measurements to low orders leads to very high correlations between
Dk and the metric tensor elements so that the correction may be
meaningless.
which has non-negligable values at quite high angles.
Limiting measurements to low orders leads to very high correlations between
Dk and the metric tensor elements so that the correction may be
meaningless.Sometimes the position of the primary beam may not be accurately known, as in the case when the diffractometer does not allow measurements at negative 2
 values,. Here we must set
values,. Here we must set 2
 true =
2
true =
2 obs - 2Dk
obs - 2Dkwhere 2Dk may be called the true zero value of 2
 . The
refinement of Dk results in a non-linear least-squares procedure for
this parameter and several cycles may be necessary to achieve convergence.
Experience shows, however, that convergence is quite fast. The maximum number
of cycles must be input after the mnemonic rz but a shift of
less than 0.002� halts the refinement. An initial value of 2
. The
refinement of Dk results in a non-linear least-squares procedure for
this parameter and several cycles may be necessary to achieve convergence.
Experience shows, however, that convergence is quite fast. The maximum number
of cycles must be input after the mnemonic rz but a shift of
less than 0.002� halts the refinement. An initial value of 2 zero
may also be given (and will be held constant unless rz
refinement is invoked). Linearisation of the expression for Q leads to
zero
may also be given (and will be held constant unless rz
refinement is invoked). Linearisation of the expression for Q leads to Q = Dk (4/
Q = Dk (4/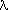 2) sin2
2) sin2
Qtrue = V*T M* V* + Dk (4/
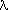 2) sin2
2) sin2
and Dk is refined as an additional parameter. The true Q and 2
 values are listed in the output. Inclusion of many
high-order
reflections is desirable but the correlation of Dk with the metric
tensor is less severe than in scheme 1 since
values are listed in the output. Inclusion of many
high-order
reflections is desirable but the correlation of Dk with the metric
tensor is less severe than in scheme 1 since  Q/Q
is proportional to
cot
Q/Q
is proportional to
cot , which decreases faster than cos2
, which decreases faster than cos2 and has large
values at low orders.
and has large
values at low orders.
LATCON should give exactly the same results as a non-linear least-squares
procedure. The errors in the variances and covariances derived from the error
propagation law, which is due to the series expansion involved, are very small
for  's of a few percent or less.
's of a few percent or less.
LATCON can also use the angle data and the crystal system stored on the archive bdf. The option line skip enables reflections to be omitted. Options also exist for outputting the refined cell dimensions.