4.31. LSABS: Absorption corrections
Authors: Eric Blanc & Dieter Schwarzenbach
Contact: Eric Blanc, Institut de Cristallographie, University of Lausanne, 1015 Lausanne, Switzerland
LSABS calculates transmission factors T, absorption-weighted mean-path
lengths T, and derivatives,
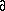 T/
T/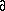 dm
dm
4.31.1. Overview
The calculation may be carried out either with an analytical method similar to
the one of de Meulenaer & Tompa (1965) or by Gaussian grid integration
(Busing & Levy, 1957). A major innovation in this program is the
calculation of the derivatives of transmission with respect to crystal shape
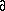 T/
T/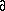 dm, where dm defines the
distance of the mth crystal face from an origin inside the crystal.
These derivatives may be used during least-squares refinement to obtain
improved estimates of the crystal shape and consequently an improved absorption
correction. The program uses crystal-based azimuthal angles (Schwarzenbach
& Flack, 1989, 1992) to define the diffraction geometry and is thus
independent of the particular instrument (diffractometer, camera, etc.)
used to collect the intensity data.
dm, where dm defines the
distance of the mth crystal face from an origin inside the crystal.
These derivatives may be used during least-squares refinement to obtain
improved estimates of the crystal shape and consequently an improved absorption
correction. The program uses crystal-based azimuthal angles (Schwarzenbach
& Flack, 1989, 1992) to define the diffraction geometry and is thus
independent of the particular instrument (diffractometer, camera, etc.)
used to collect the intensity data.
4.31.2. Methods of Absorption Correction
LSABS offers two methods of integration, the analytical method and Gaussian integration. The analytical method is more efficient than the Gaussian method in calculating the derivatives. For this reason, execution times for the two methods are comparable in the case of a coarse Gaussian grid, and in favour of the analytical method in the case of a fine Gaussian grid.
4.31.3. Analytical method
The analytical method proposed by de Meulenaer & Tompa (1965) describes the crystal shape by the set of its vertices, whereas LSABS defines it by the set of its edges. This technique facilitates an unambiguous identification of the vertices and minimizes rounding errors.
4.31.4. Gaussian grid integration
The implementation of the numerical integration of Gauss-Legendre offers a
choice of grids with 6, 8, 10 ,12, 14, 16, 24, or 32 intervals for each
dimension. For needle- and plate- shaped crystals the orientation of the grid
may be selected to lie along one of the principal directions. For a needle, the
z-axis of the grid is chosen along the needle axis identified by its zone
indices [u v w]. For a plate, the z-axis of the grid is chosen along the
plate normal identified by the face indices (h k l). The calculation of
the derivatives 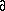 T/
T/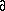 dm requires evaluation
of surface integrals. Consequently a surface grid must be specified in addition
to the 3-dimensional grid for the volume integral.
dm requires evaluation
of surface integrals. Consequently a surface grid must be specified in addition
to the 3-dimensional grid for the volume integral.
4.31.5. The Linear Absorption Coefficient �
The linear absorption coefficient � is calculated by LSABS
using the chemical formula stored on the bdf and the X-ray cross sections
stored in the program. For the moment, the available X-ray cross sections are
those for CuK , MoK
, MoK or AgK
or AgK radiation taken from Table 2.1B
of International Tables for X-ray Crystallography Vol IV (Ibers & Hamilton,
1974) for the elements from hydrogen to plutonium. For other wavelengths and
elements the value of � may be entered on the LSABS
line.
radiation taken from Table 2.1B
of International Tables for X-ray Crystallography Vol IV (Ibers & Hamilton,
1974) for the elements from hydrogen to plutonium. For other wavelengths and
elements the value of � may be entered on the LSABS
line.
4.31.6. Input and Output Data Specification
The M plane faces of a polyhedral crystal are defined by their Miller indices
(hm km lm) relative to
the lattice base a, b, c, and by the perpendicular
distances dm from a given point inside the crystal to each
face (m = 1, ..M). For the natural faces of a crystal, (hm
km lm) are integers. dm
should have been carefully measured and an estimated standard deviation of
dm should be available. The I Bragg reflections are
identified by their Miller indices hi ki
li and an instrument-independent crystal-based azimuthal
angle 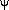 i as defined by Schwarzenbach & Flack (1989, 1992).
The above data must be available on the bdf for LSABS to
function correctly.
i as defined by Schwarzenbach & Flack (1989, 1992).
The above data must be available on the bdf for LSABS to
function correctly.
By default the nett intensities of the reflections (Schwarzenbach & Flack,
1991) are not modified by LSABS : the calculated quantities
A=1/T, <T>(i.e. Tbar) and 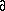 T/
T/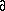 dm are simply stored on
the bdf.
dm are simply stored on
the bdf.
The recommended method of placing raw diffractometer information including crystal face indices and distance data on the bdf is first to transform a diffractometer-specific file into a CIF using DIFRAC (Flack, Blanc & Schwarzenbach, 1992). This file may then be read with CIFENT (same input lines as CIFIO) to create a bdf. This process compactly loads all of the necessary raw experimental data onto a bdf in a diffractometer-independent way.
4.31.7. File Assignments
Reads data from the input archive bdf.
Writes data to the output archive bdf.
4.31.8. Examples
title Create an absorption-corrected |F| bdf CIFENT cifin STARTX upd sgname -C 2YC REFCAL neti LSABS gauss shape needle 1 2 0 grid 10 10 24 sgrid 16 REFCAL frel SORTRF aver 1 frel |
The above example shows the use of STARTX, REFCAL, LSABS, and SORTRF to create a bdf with |Fo| data from diffractometer data produced in CIF format by the DIFRAC program. STARTX calculates the direct and reciprocal cell metrics, loads the scattering factor tables, atomic radii, and checks the symmetry information - the sgname line is necessary in STARTX as this information is not stored with the raw diffractometer data. REFCAL calculates the reflection information. LSABS performs a Gaussian grid integration and applies the absorption correction to the net intensities in the bdf. As the crystal is needle-shaped, the Gaussian grid is oriented with the needle direction [1�2�0] parallel to the grid z axis. A finer grid is defined along the needle axis than in the other directions. A second pass through REFCAL is needed to convert the net intensities to |Fo| corrected for absorption. Finally the absorption-corrected data are sorted and averaged leaving a bdf ready for structure solution and conventional |Fo| refinement.
title Create a net intensity bdf CIFENT cifin STARTX upd sgname -C 2YC REFCAL neti inst 1 incl LSABS SORTRF |
A bdf with net intensity data is created. LSABS performs an analytical absorption correction and stores the resulting values in the bdf. The bdf is suitable for the refinement of the crystal shape and decay parameters.
4.31.9. References
Blanc, E., Schwarzenbach, D. & Flack, H.D. (1991). J. Appl. Cryst. 24, 1035-1041
Busing, W. R. & Levy, H. A. (1957). Acta Cryst. 10, 180-182.
de Meulenaner, J. & Tompa, H. 1965. Acta Cryst. 19, 1014-1018.
Flack, H.D., Blanc, E. & Schwarzenbach, D. (1992) J. Appl. Cryst. 25, 455-459.
Ibers, J.A. & Hamilton, W.C. (1974) Eds. International Tables for X-rays Crystallography Vol. IV, Birmingham, England: Kynock Press
Schwarzenbach, D. & Flack, H. D. (1989). J. Appl. Cryst. 22, 601-605.
Schwarzenbach, D. & Flack, H. D. (1991). Acta Cryst. A47, 134-137.
Schwarzenbach, D. & Flack, H. D. (1992). J. Appl. Cryst. 25, 69.