Nomenclature of inorganic structure types*
Report of the International Union of Crystallography Commission on Crystallographic Nomenclature Subcommittee on the nomenclature of inorganic structure types
By J. LIMA-DE-FARIA (Chairman), Centro de Cristalografia e Mineralogia, Instituto de Investigação Científica Tropical, Alameda D. Afonso Henriques 41-4o Esq., P-1000 Lisbon, Portugal,
E. HELLNER, Fachbereich Geowissenschaften, Universität Marburg, Lahnberge, D-3550 Marburg, Federal Republic of Germany,
F. LIEBAU, Mineralogisches Institut, Universität Kiel, Olshausenstrasse 40, D-2300 Kiel, Federal Republic of Germany,
E. MAKOVICKY, Institute of Mineralogy, University of Copenhagen, OEstervoldgade 10, DK-1350 Copenhagen, Denmark
AND E. PARTHÉ, Laboratoire de Cristallographie aux Rayons-X, Université de Genève, 24 quai Ernest-Ansermet, CH-1211 Geneva, Switzerland
(Received 6 June 1989; accepted 19 July 1989 )
*Final Report accepted 15 May 1989 by the IUCr Commission on Crystallographic Nomenclature and 19 July 1989 by the IUCr Executive Committee. The nomenclature proposed in this Report is strongly recommended but is not considered as binding on IUCr publications.
Abstract
Different degrees of similarity between inorganic crystal structures are defined concisely and examples are presented that illustrate their practical application. A notation giving the coordination of atoms is presented together with some basic rules for developing crystal-chemical formulae and the Bauverband description of inorganic structure types. Typical examples of the nomenclature are: pyrite ![]() S2[(3;1)t]],
S2[(3;1)t]], ![]() FeS2
FeS2 ![]() ; spinel Mg[4]Al2[6]O4,
; spinel Mg[4]Al2[6]O4, ![]() Mg[4t]Al2[6o]O4 [1,3;12co]],
Mg[4t]Al2[6o]O4 [1,3;12co]], ![]() ,
, ![]() MgAl2O4
MgAl2O4 ![]() .
.
Introduction
Chemical formulae in inorganic crystal structure papers often give very little structural information. This is due partly to the existence of several different notations in the literature and partly to the lack of a single generally accepted nomenclature. In addition, relationships between structures, such as isotypism and homeotypism, are described differently.
The Ad hoc Meeting on the Nomenclature of Inorganic Structure Types, sponsored by the IUCr Commission on Crystallographic Nomenclature at the 13th International Congress of Crystallography in Hamburg on 11 August 1984, prompted the Commission to appoint a Provisional Subcommittee to study the problems discussed [see Acta Cryst. (1986). A42, 64 for the Subcommittee membership]. The progress subsequently made at an informal meeting in Lisbon led to recognition of the Provisional Subcommittee as a regular Subcommittee of the Commission on 19 August 1985.
In the present Report, the Subcommittee proposes concise definitions for different degrees of similarity between inorganic structure types and a detailed notation for the coordination of atoms. Basic rules for developing crystal-chemical formulae and Bauverband descriptions are recommended as well. The primary aim is to promote, although not to enforce, the use of crystal-chemical formulae instead of traditional chemical formulae which contain no structural information.
This Report was prepared during four meetings of the Subcommittee, the first held in Lisbon (April 1985), the others in Marburg (February 1986), Geneva (December 1986), and Copenhagen (March 1988). It represents an extension and updating of pioneering concepts on crystal-chemical formulae by Machatschki (1928, 1947, 1953), Bragg (1930) and Bokii (1954), and on lattice complexes by Niggli (1919, 1945), Laves (1930) and Hermann (1960).
I. Terms that define different degrees of similarity between inorganic structures
The following hierarchy of terms is considered based on the degree of structural similarity: isopointal, isoconfigurational, crystal-chemically isotypic, and homeotypic structures. Other relationships of interest are also listed.
I.1. Two structures are defined as isopointal if :
(i) they have the same space-group type (as defined in IT, ![]() 8.2.1)
8.2.1) ![[*]](https://www.iucr.org/__data/assets/image/0015/12534/foot_motif.gif) or belong to a pair of enantiomorphic space-group types; and
or belong to a pair of enantiomorphic space-group types; and
(ii) the atomic positions, occupied either fully or partially at random, are the same in both structures, i.e. the complete sequence of the occupied Wyckoff positions (including the number of times each Wyckoff position is occupied) is the same for both structures when the structural data have been standardized.
As there are no limitations on the values of the adjustable parameters of the Wyckoff positions (as used in IT ) or on the cell parameters, isopointal structures may have different geometric arrangements and atomic coordinations.
Two structures may be shown to be isopointal if they can be described in such a way that corresponding occupied Wyckoff positions have the same Wyckoff letters; to achieve this, it may be necessary to shift the origin and/or rotate/permute the coordinate system. This can be done by application of the affine normalizer (IT ![]() 8.3.2 and 14.1) or by standardization procedures (Parthé & Gelato, 1984; Gelato & Parthé, 1987).
8.3.2 and 14.1) or by standardization procedures (Parthé & Gelato, 1984; Gelato & Parthé, 1987).
I.2. Two structures are defined as isoconfigurational (configurationally isotypic ) if:
(i) they are isopointal; and
(ii) for all corresponding Wyckoff positions, both the crystallographic point configurations (crystallographic orbits![[*]](https://www.iucr.org/__data/assets/image/0015/12534/foot_motif.gif) ) and their geometrical interrelationships are similar.
) and their geometrical interrelationships are similar.
These conditions require the entire configurations of the two structures to be similar. Consequently, all geometrical properties, such as axial ratios, angles between crystallographic axes, values of corresponding adjustable positional parameters (x, y, z), and coordinations of corresponding atoms are similar. The term 'similar' used in this definition is discussed below.
Standardization procedures may be necessary to test whether two structures are isoconfigurational.
I.3. Two structures are defined as crystal-chemically isotypic if:
(i) they are isoconfigurational; and
(ii) the corresponding atoms and corresponding bonds (interactions) have similar physical/chemical characteristics.
Crystal-chemical isotypism may be defined in different ways, depending on the number and nature of the physical/chemical characteristics that are taken into consideration, such as bond strength distribution, bond character, electronegativities assigned to atoms, radius ratios assigned to pairs of atoms, and electronic states.![[*]](https://www.iucr.org/__data/assets/image/0015/12534/foot_motif.gif)
The use of the term 'similar', in the definitions of configurational and crystal-chemical isotypism, arises from the inherent difficulty in defining a priori limits on the similarity of geometrical configurations or physical/chemical characteristics. These limits may differ between different categories of structures; they may also differ according to the purpose of a particular investigation or the physical or chemical property studied. Several approaches are possible in defining limits, such as a priori considerations (modelling) or statistical studies of known structure categories. Different approaches may yield different results. Examples of crystal-chemical isotypes are given in Table 1. Another example is the low-pressure and high-pressure forms of Ce which are crystal-chemically isotypic with regard to most crystal-chemical criteria; they are, however, not crystal-chemical isotypes with regard to electronic states.
| Pnma | I4/mmm | |||||||
| 4(a), 8(c)xxx | 2(a),4(e) c/a=2.52-c/a=3.30 | 16(a),24(c), 24(d),96(h)xyz | 4(a) | 4(a),4(e) | 4(a),8(c) | 4(a),8(c)xxx | ||
| LuRuB2-ScRhSi2 | FeS2(pyrite)-CO2 | ZrPd2-Zr2Pd | Ca3Al2Si3O12-Y3Fe 3+5O12 | Cu-Ne | NaCl-PbS | CaF2-Li2O | FeS2(pyrite)-PtP2 | |
| Isopointal | No | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Isoconfigurational | - | No | * | Yes | Yes | Yes | Yes | Yes |
| Crystal-chemically isotypic according to | ||||||||
| bond-strength distribution | - | - | Yes | No | Yes | Yes | Yes | Yes |
| bond character | - | - | Yes | No | No | No | Yes | Yes |
| radius ratios assigned to pairs of corresponding sites | - | - | No | Yes | Yes | Yes | No | Yes |
| electronegativities assigned to sites | - | - | Nearly yes | Yes | No | Yes | No | Yes |
*Notice that in this case the two structures which have c/a ratios differing by 30% are isoconfigurational if the limit of similarity is set above 30% and non-isoconfigurational if it is set below 30%.
I.4. Two structures represent a type and antitype if:
(i) they are isoconfigurational; and
(ii) some important physical/chemical characteristics of corresponding atoms are interchanged (reversed).
The characteristics usually considered in this context are electronegativities (positive versus negative charges) and larger versus smaller radii.
Examples are: CaF2-Li2O (Table 1), LaF3-Cu3P, CaCl2-Co2C, NaCl-RbF.
I.5. Two structures are defined as homeotypic if one or more of the following conditions required for isotypism are relaxed:
(i) identical or enantiomorphic space-group types, allowing for group-subgroup and group-supergroup relationships;
(ii) limitations imposed on the similarity of geometric properties, i.e. axial ratios, interaxial angles, values of adjustable positional parameters, and the coordination of corresponding atoms;
(iii) site occupancy limits, allowing given sites to be occupied by different atomic species.
The present definition narrows the original concept of Laves (1980). Two structures are considered as homeotypic if all essential features of topology are preserved between them. Relaxation of the geometric limits as in I.5(ii) without relaxation of the isosymmetry condition leads to structure type branches.
Examples of homeotypic structures are:
Distortion variants (or distortion derivatives): CaTiO3 (ideal perovskite) ![]() KCuF3, BaTiO3, GdFeO3, etc. with subgroup symmetries.
KCuF3, BaTiO3, GdFeO3, etc. with subgroup symmetries.
Site-ordering variants (or substitution derivatives): C (diamond) ![]() ZnS (sphalerite)
ZnS (sphalerite) ![]() Cu3SbS4 (famatinite)
Cu3SbS4 (famatinite) ![]() Cu2FeSnS4 (stannite); K(Al0.25Si0.75)4O8 (sanidine)
Cu2FeSnS4 (stannite); K(Al0.25Si0.75)4O8 (sanidine) ![]() KAlSi3O8 (microcline).
KAlSi3O8 (microcline).
I.6. Polytypic structures are defined in the Report of the IUCr Ad-hoc Committee on the Nomenclature of Disordered, Modulated and Polytype Structures (Guinier et al., 1984).
Examples are: closest-packed structures of chemical elements, SiC polytypes, Friauf-Laves phases, micas.
I.7. Interstitial (or 'stuffed') derivatives represent compounds in which unoccupied 'interstitial' sites (voids) of the basic structure are (progressively) filled by atoms in the derivative structure. In general, the relationship between the unfilled parent (basic) structure and the derivatives based on filling one specific interstitial site approaches homeotypism.
Examples are: ReO3  CaTiO3; Mg
CaTiO3; Mg  Mo2C; SiO2 ('ideal' tridymite)
Mo2C; SiO2 ('ideal' tridymite)  KNa3(AlSiO4)4 (nepheline).
KNa3(AlSiO4)4 (nepheline).
I.8. 'Recombination' structures are formed when topologically simple parent structures are periodically divided into blocks,![[*]](https://www.iucr.org/__data/assets/image/0015/12534/foot_motif.gif) rods or slabs which in turn are recombined into derivative structures by means of one or more structure building operations.
rods or slabs which in turn are recombined into derivative structures by means of one or more structure building operations.
The most important of these operations are (1) unit-cell twinning, (2) crystallographic shear planes, (3) intergrowth of blocks, rods or slabs of different structure types, (4) periodic out-of-phase or antiphase boundaries, (5) rotation of rods (blocks) and (6) the vernier principle (Makovicky & Hyde, 1981). For most of these operations, not only parallel but also cyclic examples have been observed. In general, the sites on block, rod or slab interfaces differ in coordination and chemistry from those in the interior. This interface modulation can be accompanied or substituted by an overall long-range compositional modulation.
In cases (1) to (5), the frequency of structure building operators (or, conversely, the size of 'undisturbed' structure blocks, rods or slabs between two consecutive operators) can vary by well defined increments so that these phases often occur as members of homologous series.
Examples are:
Twinning on unit-cell scale: PbS ![]() lillianite homologous series (Pbn-1Bi2Sn+2), e.g. Pb3Bi2S6 (lillianite).
lillianite homologous series (Pbn-1Bi2Sn+2), e.g. Pb3Bi2S6 (lillianite).
Shear derivatives: TiO2 (rutile) ![]() TinO2n-1 (Magnéli phases) or TiO2 (rutile)
TinO2n-1 (Magnéli phases) or TiO2 (rutile) ![]() Nb2O5.
Nb2O5.
Intergrowth on unit-cell scale: olivine-norbergite homologous (polysomatic) series n(Mg,Fe)2SiO![]() Mg(OH,F)2; biopyriboles, e.g. Mg3n+1Si4nO10n+2(OH) 2n-2; MgCu2-type and CaCu5-type slabs
Mg(OH,F)2; biopyriboles, e.g. Mg3n+1Si4nO10n+2(OH) 2n-2; MgCu2-type and CaCu5-type slabs ![]() Ce2Ni7.
Ce2Ni7.
Antiphase boundaries: CuAu II, Dy5Cl11.
Block (rod) rotation: ReO![]() Nb8W9O47 or ReO
Nb8W9O47 or ReO![]() Mo5O14.
Mo5O14.
Vernier principle: slabs PbS (100) and PbS (111) ![]() Pb46Bi54S127 (cannizzarite), Y6O5F8, Pb2Bi2S5 (cosalite), NdCo4B
Pb46Bi54S127 (cannizzarite), Y6O5F8, Pb2Bi2S5 (cosalite), NdCo4B![]() Sm17(Fe4B4)15.
Sm17(Fe4B4)15.
Compositional modulation: Pb46Bi54S127 (cannizzarite), FePb3Sn4Sb2S14 (cylindrite).
Note : In each example the sequence indicated is: parent(s) ![]() derivative(s).
derivative(s).
II. Coordination of the atoms
The coordination number [N] of an atom is given by the number of coordinating atoms: the definition of 'coordinating atoms' depends on the bonding model, the nature of the problem and the calculation methods. The coordination polyhedron of an atom is the polyhedron that has vertices coincident with the centres of coordinating atoms. In structures which contain lone electron pairs and in which volumes ascribable to these lone electron pairs are comparable with the volumes of individual atoms, coordination polyhedra can be considered that include lone electron pairs as some of the vertices.
Several methods have been proposed to define coordination numbers in complicated structures. Most yield a 'weighted' coordination number resulting from a form of weighting the coordinating atoms according to their distances from the central atom, e.g. by means of Voronoi polyhedra (Wirkungsbereiche, Dirichlet domains) with or without consideration of the atomic radii (Frank & Kasper, 1958, 1959; Bruzzone, Fornasini & Merlo, 1970; Brunner & Schwarzenbach, 1971; Fischer, Koch & Hellner, 1971; Brunner, 1977; O'Keeffe, 1979; Hoppe, 1979).
This Subcommittee proposes, as an improvement of earlier notations (Machatschki, 1947; Donnay, Hellner & Niggli, 1964; Lima-de Faria & Figueiredo, 1976), a specific set of symbols for the most commonly observed types of coordination polyhedra. These coordination symbols are added as trailing superscripts to the symbols used for the chemical elements in crystal-chemical formulae and, preferably, are placed between square brackets.![[*]](https://www.iucr.org/__data/assets/image/0015/12534/foot_motif.gif)
For another use of these symbols, see the Bauverband approach (![]() IV and Hellner, 1965).
IV and Hellner, 1965).
Two levels of symbols are proposed, complete and simplified.
(1) Each complete symbol gives the total number of atoms coordinated to a central atom A. The type of coordination polyhedron is indicated by lower-case letters. The most common coordination polyhedra are listed in Table 2; for example,
![]()
| Coordination polyhedron around atom A | Complete symbol | Simplified symbols | IUPAC symbol | ||
| Single neighbour | [1l] | [1] | |||
| Two atoms collinear with atom A | [2l] | L-2 | |||
| Two atoms non-collinear with atom A | [2n] | A-2 | |||
| Triangle coplanar with atom A | [3l] | TP-3 | |||
| Triangle non-coplanar with atom A | [3n] | TPY-3 | |||
| Triangular pyramid with atom A in the centre of the base | [4y] | ||||
| Tetrahedron | [4t] | [t] | t | T-4 | |
| Square coplanar with atom A | [4l]* | [s] | s | SP-4 | |
| Square non-coplanar with atom A | [4n] | SPY-4 | |||
| Pentagon coplanar with atom A | [5l] | ||||
| Tetragonal pyramid with atom A in the centre of the base | [5y] | SPY-5 | |||
| Trigonal bipyramid | [5by] | TBPY-5 | |||
| Octahedron | [6o] | [o] | o | OC-6 | |
| Trigonal prism | [6p] | [p] | p | TPR-6 | |
| Trigonal antiprism | [6ap] | [ap] | ap | ||
| Pentagonal bipyramid | [7by] | PBPY-7 | |||
| Monocapped trigonal prism | [6p1c] | TPRS-7 | |||
| Bicapped trigonal prism | [6p2c] | TPRT-8 | |||
| Tetragonal prism | [8p] | ||||
| Tetragonal antiprism | [8ap] | ||||
| Cube | [8cb] | [cb] | cb | CU-8 | |
| Anticube | [8acb] | [acb] | acb | SAPR-8 | |
| Dodecahedron with triangular faces | [8do] | [do] | do | DD-8 | |
| Hexagonal bipyramid | [8by] | HBPY-8 | |||
| Tricapped trigonal prism | [6p3c] | [9] | TPRS-9 | ||
| Cuboctahedron | [12co] | [co] | co | ||
| Anticuboctahedron (twinned cuboctahedron) | [12aco] | [aco] | aco | ||
| Icosahedron | [12i] | [i] | i | ||
| Truncated tetrahedron | [12tt] | ||||
| Hexagonal prism | [12p] | ||||
| Frank-Kasper polyhedra with: | |||||
| 14 vertices | [14FK] | [14] | |||
| 15 vertices | [15FK] | [15] | |||
| 16 vertices | [16FK] | [16] |
*Also [4s].
Some of the principles which have been adopted for creating coordination symbols and which can be used for possible extension are as follows:
[Nn] denotes an N-sided non-coplanar coordination polygon around atom A;
[Nl] denotes an N-sided coplanar (collinear for N < 3) coordination polygon around A;
[Np] denotes an N/2-sided coordination prism around A;
[Ny] denotes an (N - 1)-sided coordination pyramid around A;
[Nby] denotes an (N - 2)-sided coordination bipyramid around A.
In addition to these systematically derived symbols, Table 2 also contains the corresponding symbols recommended by IUPAC (1990).
(2) The simplified symbol requires only the coordination number [N], without specifying the polyhedron type. On the other hand, for the most common coordination polyhedra, a simplified letter notation can be used as a trailing superscript with or without square brackets (t for tetrahedron, o for octahedron, cb for cube etc., as in Table 2); for example,
![]()
Coordination polyhedra which include one or several lone electron pairs as vertices can be denoted as follows: [![]() ] (equivalent to [3n]), [
] (equivalent to [3n]), [![]() ], [
], [![]() ] (equivalent to [5y]) and [
] (equivalent to [5y]) and [![]() ] etc.
] etc.
The notation must be able to describe coordination by different sets of atoms, or coordination at different (sets of) distances, or self-coordination and coordination polyhedra composed of several distinct atomic species, in addition to giving the shape of coordination polyhedra and/or the number of coordinating atoms. The notation should also be flexible and able to express either the complete coordination or only the desired limited amount of information. The notation rules recommended by this Subcommittee are outlined in the following paragraphs.
For normal oxycompounds, a simple coordination notation such as that for perovskite, CaTiO3:
![]()
![]()
However, in the general case such simplification results in substantial loss of information and ambiguity of interpretation. The coordination of atom A in compound AaBbCc for such a case is written as
A[m,n;p]
where m and n denote the numbers of atoms B and C (i.e. always in the sequence given in the formula) which are coordinated to atom A. These coordination numbers are separated by commas. The self-coordination number p of A by atoms A follows the semicolon. The coordination of atom B is then written as![]()
For example, more complete information on perovskite reads:
| Ti | O | Ca | Ca | O | Ca | Ti | O |
| Ca[8cb,12co;6o] | Ti[8cb,6o;] | O3[4l,2l;8p]. | |||||
The element symbols above the superscripts merely indicate the species to which the given coordination symbol applies and are not part of the coordination terminology. The crystal-chemical formula can be simplified as follows:
![]()
![]()
Further simplifications for perovskite have been given above.
As another example, atom A may be considered to be tetrahedrally coordinated by three B atoms and one C atom. In addition, atom A may be coordinated by a cuboctahedron of twelve A atoms. Its coordination can then be described in the following ways:
A[(3,1)t;12co], A[3,1;12], A[(3,1)t], A[;12], A[t;], A[t], A[;co].
For pyrite, cubic FeS2, the coordination is described as
![]()
![]()
If in a compount AaBb, B is coordinated to A at two different distances or at two distinct distance ranges (1 and 2), then the coordination is written as
A[(m1+m2);(p1+ p2)].
For example, ![]() -SnS:
-SnS:
![]()
NaCu4(AsO4)3: if only coordination of cations by oxygen is of interest,
![]()
![]()
III. Nomenclature for crystal-chemical formulae
III.1. General remarks
An acceptable nomenclature for crystal-chemical formulae should exhibit the following general characteristics:
(1) It should be as simple and self-explanatory as possible.
(2) It should retain the chemical symbols of the elements and, whenever possible, follow the normal rules of chemical formulae.
(3) It should retain other widely used symbols (e.g. coordination number, dimensionality etc.) as far as possible.
(4) It should not introduce symbols which are already widely used but with a different meaning.
(5) It should be flexible, allowing symbols to be eliminated for simplification, or permitting the inclusion of extra symbols for additional information.
(6) It should be easy to print and suitable for computer use.
The proposed nomenclature for crystal-chemical formulae is based on the distribution of bond strengths. The spatial distribution of bond strengths in a structure can be either homogeneous or heterogeneous. If the distribution is heterogeneous, certain atoms![[*]](https://www.iucr.org/__data/assets/image/0015/12534/foot_motif.gif) are more tightly bonded together than others, resulting in finite groups or in assemblages that are infinite in one, two or three dimensions. These assemblages are considered as structural units and the remaining atoms as interstitial atoms.
are more tightly bonded together than others, resulting in finite groups or in assemblages that are infinite in one, two or three dimensions. These assemblages are considered as structural units and the remaining atoms as interstitial atoms.
If the spatial bond-strength distribution is homogeneous, two limiting situations may be discerned: either the structure is based on a three-dimensional framework (examples are diamond or cristobalite with directional bonds), or it is simply a packing of individual atoms (examples are helium, copper or sodium chloride with non-directional bonds). The corresponding sructural units are thus either a framework or the individual atoms, respectively.
There are five main categories of structural units, according to the kind of bond-strength distribution:
| Dimensionality of structural unit | Category of structural unit | |
| 0-dimensional | 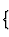 |
individual atoms |
| groups (i.e. rings, chain fragments, cages) | ||
| 1-dimensional | chains | |
| 2-dimensional | sheets | |
| 3-dimensional | frameworks. |
A structural unit may be considered to consist of subunits such as single atoms, polyhedra, single rings, single chains or single layers.
A structure can be considered to consist of structural units packed together, with interstitial atoms located between them. If the structural unit is a framework, the interstitial atoms or groups of atoms occupy holes within the framework.
Since the strengths of bonds cannot always be accurately quantified, some ambiguity may exist in assigning a structure to a given category.
III.2. Fundamental features of notation
III.2.1. General crystal-chemical formulae. Crystal-chemical formulae give detailed structural information on the structural unit(s), their constitution, the packing scheme, the interstitial atoms, and the coordination of the atoms (both interstitial and those contained in the structural units).
Symbols for atoms belonging to the structural unit(s) are placed between square brackets, [ ], and the packing information between angle brackets, ![]() . The information on constitution which relates to the structural unit as a whole is placed within curly brackets, { }. However, the constitutional information which relates to subunits of the structural unit(s) may be expressed either within curly brackets or as trailing superscripts to the chemical elements or subunits inside the structural unit.
. The information on constitution which relates to the structural unit as a whole is placed within curly brackets, { }. However, the constitutional information which relates to subunits of the structural unit(s) may be expressed either within curly brackets or as trailing superscripts to the chemical elements or subunits inside the structural unit.
Curly brackets with constitutional information precede and angle brackets for packing information immediately follow the structural unit to which they refer.
Information concerning interstitial atoms and/or groups of atoms should generally be placed before or after that on the structural unit(s) in the sequence that chemical formulae are usually written.
In accordance with IUPAC (1990) rules, the valency state of each atom is expressed immediately after its chemical symbol by a Roman numeral in parentheses [e.g. Fe(III)], a superscripted Roman numeral (e.g. Fe![]() ), or by a superscripted Arabic numeral followed by the sign + or - (e.g. Fe3+).
), or by a superscripted Arabic numeral followed by the sign + or - (e.g. Fe3+).
The coordination of each atom, either interstitial or in the structural unit, is expressed within square brackets as a trailing superscript to the chemical symbol. If additional constitutional information related to subunits is given within the square brackets for the structural unit, then it should be placed between Japanese quotation marks (called 'brackets') below), ![]() , as an additional trailing superscript:
, as an additional trailing superscript: ![]() .
.
The general notation for a compound AaBbCc DdEeF f Gg could thus be:
| interstitial atoms | constitution of structural unit | structural unit | packing of structural units | interstitial atoms. |
Examples are given in ![]() III.2.2 and Table 3.
III.2.2 and Table 3.
| Compound | Crystal-chemical formulae with different structural interpretations and degrees of simplification | Bauverband description (lattice-complex notation) | |||||
| He (hex.) | He | P63/mmc | |||||
| Cu | Cu | Fm3m | |||||
| C (diamond) | C | ||||||
| NaCl | NaCl | Fm3m | |||||
| SiO2 (quartz) | SiO |
P6222 | |||||
| SiO2 (cristobalite) | SiO |
||||||
| FeS2 (pyrite) | FeS |
||||||
| FeS2 (marcasite) | FeS |
Pmnn | |||||
| (Mg,Fe)2SiO4 (olivine) | Pmcn | ||||||
| MgAl2O4 (spinel) | |||||||
| CaMgSi2O6 (diopside) | |||||||
| KAl3Si3O10(OH)2 (muscovite) | |||||||
| LaP2 (HT form) | |||||||
| Ba3AlSb3 | |||||||
| Ca3AlAs3 | |||||||
| (Mn,Fe)AlPO4(OH)2H2O (eosphorite) | |||||||
| Na3AlF6 (cryolite) | |||||||
| Ca3Si2O7 (rankinite) | |||||||
| Ca3Si2O7 (kilchoanite) | |||||||
If several distinct structural units are present, each is considered separately with its information in curly brackets followed by that in square brackets, for example:
![]()
The packing information within angle brackets describes the way the two different structural units pack together.
The hierarchy of bonds leads to a hierarchy of structural units when several degrees of bond strengths may be discerned in a structure. This often leads to weaker bond-strength units incorporating previous more strongly bonded units, and can be expressed by multiple brackets, with the central brackets referring to the structural unit having the strongest bonds:
![]()
The proposed formula can be used with any amount of any selection of structural information depending on the purpose of the study; see below.
III.2.2. Constitution of structural units. The constitution of a structural unit expresses its extensional and geometrical 'structural'. i.e. the way the structural unit is built from its subunits, which may be polygons, polyhedra or any other clusters.
Some of the constitutional aspects are concerned with the structural unit as a whole, whereas other aspects are only concerned with the way each subunit is linked to other subunits. The former include dimensionality, multiplicity, branchedness and periodicity.
(i) The dimensionality is the number of dimensions in which a structural unit has infinite extension. It is zero for individual atoms and finite groups and one, two or three for infinite chains, sheets and frameworks, respectively. The corresponding symbols to be used in a crystal-chemical formula are ![]() and
and ![]() .
.
The following specific symbols may be used instead of ![]() for 0-dimensional structural units:
for 0-dimensional structural units:
| individual atom: {a} | |||
| group: {g} | 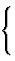 |
ring: |
|
| chain fragment: |
|
||
| cage: |
|
||
Examples are: Cs![]() S6], Na
S6], Na![]() Si4], Cu6{r}[Si6O18].6H2O.
Si4], Cu6{r}[Si6O18].6H2O.
If dimensionality is the only information expressed, the ![]() and the pictorial symbols
and the pictorial symbols![[*]](https://www.iucr.org/__data/assets/image/0015/12534/foot_motif.gif) may be used without curly brackets. Otherwise, curly brackets are compulsory in order to avoid ambiguity.
may be used without curly brackets. Otherwise, curly brackets are compulsory in order to avoid ambiguity.
The symbol {a} is not needed when several individual atoms, ![]() , considered as structural units, are written
, considered as structural units, are written ![$[A] [B] [C]\dots$](https://www.iucr.org/__data/assets/image/0005/12398/img126.gif) . When only one atom symbol is placed within square brackets, it means that the structural unit is reduced to an individual atom. However, if the same atom symbols are written [ABC], then it is necessary to add {a} in front of the square brackets.
. When only one atom symbol is placed within square brackets, it means that the structural unit is reduced to an individual atom. However, if the same atom symbols are written [ABC], then it is necessary to add {a} in front of the square brackets.
In the case of group structures, e.g. ring, chain fragment, and cage structures, the number of atoms of each chemical element within square brackets must be equal to the number of atoms of each chemical element in the finite group.
(ii) The multiplicity of a structural unit is the number of single subunits, e.g. polyhedra, single rings, single chains or single layers which are linked to form a complex structural unit of the same dimensionality.
(iii) With regard to branchedness, finite structural units and single chains are called unbranched if they contain no subunits that are linked to more than two other units. They are called branched if they do. In addition, complex structural units, which can be considered as formed by linking unbranched (branched) finite structural units or single chains, are described as unbranched (branched).
(iv) The periodicity of a structural unit of infinite extension is the number of subunits, excluding branches, within one repeat unit of the chain from which the structural unit can be generated by successive linking.
For details of concepts under (ii)-(iv) see Liebau (1982, 1985); a publication on their usage in the present formulae is in preparation.
The main constitutional aspects concerned only with the way each subunit is linked to the other subunits are linkedness and connectedness.
(i) The linkedness is the number L of peripheral atoms shared between two subunits. The value of linkedness is zero for an isolated subunit. It is one or two for two subunits sharing a corner or an edge, respectively, and it is three or more for two subunits sharing a face. The average linkedness value of a subunit may be non-integral if the given subunit shares corners plus edges with different adjacent subunits.
(ii) The connectedness of a subunit is the total number s of adjacent subunits with which it shares common atoms, irrespective of its linkedness with a particular adjacent subunit. A subunit may be singular (isolated), primary (linked to only one other subunit), secondary (linked to two others), etc.
The specific values L1, L2 etc. of linkedness and/or s of connectedness of a subunit are written within 'Japanese brackets' as trailing superscripts to its central atom, by analogy with the coordination symbols. The first entries in the Japanese brackets are the different values of Ln, separated from the value of s by a semicolon. The general formula for a structural unit with only one kind of subunit then reads
[Am[L1,L 2,..;s]Bn].
For example, SiO2 exists in a number of polymorphs having different values of linkedness and connectedness of the SiO4 tetrahedra:
fibrous silica:
![]()
quartz, cristobalite, coesite etc. :
![]()
and stishovite
![]()
A structural unit can often be generated from a part of either lower or the same dimensionality by a simple geometrical process that usually represents an infinitely repeated translation. This imaginary geometrical process is called condensation because it emphasizes the way a chain can be generated from a group, a sheet from a chain, and a framework from a sheet. It also reveals certain similarities between different structural units, and a specific composite notation for the structural units has been developed which emphasizes this interrelationship (![]() V).
V).
III.2.3. Packing of structural units. The packing of structural units expresses the three-dimensional arrangement in space. When the structural units are individual atoms, the known nomenclature for describing the packing of atoms (three-dimensional and layer-stacking descriptions) may be used. When the structural units are groups, their centres of gravity may be used with the same nomenclature as for the packing of atoms. However, this will be an incomplete description because of the lack of information on the orientation of the groups.
Packing of structural units in structures based on groups, infinite chains or sheets may be treated by layer description. Such a layer description consists of slicing the structure into layers which, by stacking, completely generate the original crystal structure. Structural units should be preserved intact in the process of slicing. The structure is then described by the packing of structural units in the layer and by a set of stacking operators.
The layer description can also be applied to framework structures taking into consideration the fact that the units operated upon are parts of a single framework.
With respect to the nomenclature for the packing of structural units, only the symbols for cubic closest packing, c, and hexagonal closest packing, h, and their sequential combination are adopted here. When no other packing information is provided these symbols may be given as trailing superscripts to the square brackets which contain the structural unit. In this case, angle brackets are not compulsory. Any other packing information, particularly the packing (or stacking) symbolism used by individual authors should be given in angle brackets on the line.
![]()
If packing information is to be given for a set of atoms which does not constitute a structural unit, the symbol should be placed within vertical bars followed by the packing information:
![]()
IV. The Bauverband approach
The Bauverband terminology offers a brief description of crystal structures that can be used for explaining relationships between structure types as well as for their classification, recognition of configurational isotypes and for the retrieval of structures with specified relationships.
A crystallographic Bauverband may be defined as a three-dimensionally periodic arrangement of points occupied by atoms or polyhedra of atoms with definite geometric properties: it represents a connectivity pattern typical for a given structure type and it represents, or approximates, a sphere packing with typical self-coordination and with several types of voids for interstitial atoms. The arrangement of such points in a unit cell with specified space group may be described by the parameters of one point position (homogeneous Bauverband) or by the parameters of two or more independent point positions (heterogeneous Bauverband). A Bauverband is described by a combination of applicable original or transformed invariant lattice complexes [henceforth denoted as invariant LC] (IT ![]() ), together with a symbol for the circumscribed coordination polyhedra and their orientation (when applicable).
), together with a symbol for the circumscribed coordination polyhedra and their orientation (when applicable).
The Bauverband describes the essential part of the structure type. Positions of atoms not involved in the Bauverband are described using the same symbolism as used for the Bauverband. To explore different structure-type relationships, different Bauverband symbols or even choices can be selected in the same structure. The Bauverband is designated by bold-face characters and bold-face square brackets in the structure-type symbol.
The invariant LC in the characteristic Wyckoff positions are represented mainly by capital letters ; LC with equipoints at the nodes of the Bravais lattice are designated by their appropriate lattice symbols: P, A, B, C, I, F, R (Hermann, 1960). The other invariant complexes are designated by letters that recall some structural features of a given complex, for example: D (derived from the diamond structure), E (hexagonal close packing), Q (Si atoms in high-temperature quartz), W (![]() -W structure), as well as the two-dimensional complexes G (graphite layer) and N (Kagomé net). Invariant LC in their standard descriptions are given in Table 14.3 of IT.
-W structure), as well as the two-dimensional complexes G (graphite layer) and N (Kagomé net). Invariant LC in their standard descriptions are given in Table 14.3 of IT.
Those special point configurations of variant LC which have higher symmetry than the symmetry of the variant LC itself, i.e. the so-called limiting complexes (Grenzkomplexe) (IT ![]() 14.3.2) can also be employed in Bauverband symbolism. Such point configurations are designated by the applicable invariant LC symbols plus small letters showing the direction of positional freedom, e.g. Fxxx in site 4(a) of space group P213.
14.3.2) can also be employed in Bauverband symbolism. Such point configurations are designated by the applicable invariant LC symbols plus small letters showing the direction of positional freedom, e.g. Fxxx in site 4(a) of space group P213.
Some of the non-standard settings of an invariant LC can be described by a shifting vector added in front of the symbol. The shifting vector is given in terms of fractional coordinates; for example, in the CsCl structure type, Cl is considered the Bauverband which is expressed as CsCl, and the entire structure type is described as ![]() . The most common shifting vectors have been abbreviated:
. The most common shifting vectors have been abbreviated: ![]() represents
represents ![]() represents
represents ![]() and
and ![]() represents
represents ![]() ; for example
; for example ![]() represents NaCl whereas
represents NaCl whereas ![]() represents sphalerite, ZnS.
represents sphalerite, ZnS.
In many structures, the unit cell represents for certain atoms a multiple of the basic cell in standard setting, e.g. the unit cell of spinel represents for oxygen atoms a 2 ![]() 2
2 ![]() 2 multiple of the standard F-centred cell. In general, a transformation matrix which expresses the new basis vectors in terms of the standard ones must be given. The order of the transformation matrix is given by the value of the determinant of this matrix, e.g. 8 in the above case. Thus, the Bauverband description for spinel is MgAl2O4 and
2 multiple of the standard F-centred cell. In general, a transformation matrix which expresses the new basis vectors in terms of the standard ones must be given. The order of the transformation matrix is given by the value of the determinant of this matrix, e.g. 8 in the above case. Thus, the Bauverband description for spinel is MgAl2O4 and ![]() . Fxxx in this formula expresses the fact that in the new cell oxygen is described by a limiting complex with
. Fxxx in this formula expresses the fact that in the new cell oxygen is described by a limiting complex with ![]() . Mg forms the D and Al the
. Mg forms the D and Al the ![]() point configuration.
point configuration.
For complicated structures, efficient description can be achieved if complicated atomic configurations are understood as polyhedra - centred or not, connected or isolated - which are circumscribed about the points of an invariant LC. The same symbolism was chosen for these polyhedra as is used for coordination polyhedra in Table 2. However, centred polyhedra are specified by a dot, e.g. [.4t], the empty ones by a small square, e.g. [![]() 4t]. The linkedness of these polyhedra, i.e. corner, edge and face sharing is described by subscripts c, e and f, respectively. These are equivalent to L = 1, 2 and 3 or more in
4t]. The linkedness of these polyhedra, i.e. corner, edge and face sharing is described by subscripts c, e and f, respectively. These are equivalent to L = 1, 2 and 3 or more in ![]() III.2.2. The mutual orientation of these polyhedra is expressed by selected symmetry operations of the space group which are given as a symbol preceding the capital letter.
III.2.2. The mutual orientation of these polyhedra is expressed by selected symmetry operations of the space group which are given as a symbol preceding the capital letter.
Examples are: ![]() for SiF4 in
for SiF4 in ![]() ;
; ![]() (or
(or ![]() + I for W
+ I for W![]() in
in ![]() and
and ![]() + W in
+ W in ![]() (i.e. U
(i.e. U![]() in
in ![]() with the diagonal glide plane ..n generating the second icosahedron [12i] at
with the diagonal glide plane ..n generating the second icosahedron [12i] at ![]() in contrast to the translation symmetry in the previous case.
in contrast to the translation symmetry in the previous case.
If the Bauverbände in a set of structures belong to the same point configuration (the same LC), they form a family. Families are divided into main classes according to the transformation matrix and/or according to splitting of the 'parent' LC (Hellner, 1986). Structure types which can be described by the subtraction of one or more LC from the 'parent' LC of a main class form subclasses. Examples selected from the F family are: ![]() (1st order) describes Cu, ZnS, PbS etc. whereas
(1st order) describes Cu, ZnS, PbS etc. whereas ![]() describes Re
describes Re![]() , CaTi
, CaTi![]() etc.;
etc.; ![]() (8th order) describes spinel, MgAl
(8th order) describes spinel, MgAl![]() , and pentlandite, (Ni, Fe, Co)
, and pentlandite, (Ni, Fe, Co)![]() , whereas the subclass
, whereas the subclass ![]() describes tetrahedrite, Cu12Sb
describes tetrahedrite, Cu12Sb![]() .
.
For structures in which layer description is essential, two-dimensional LC have been used together with corresponding layer-stacking sequences (Hellner, 1986).
V. Examples and further references
Examples presented in Table 3 have been selected in such a way as to show the flexibility of choice between various formulae (notations) as well as the flexibility in amount of information included or omitted, depending on the purpose of the study. It should be noted that at some stage of simplification the formulae may describe a group of structure types related through common crystal-chemical features rather than a single structure type.
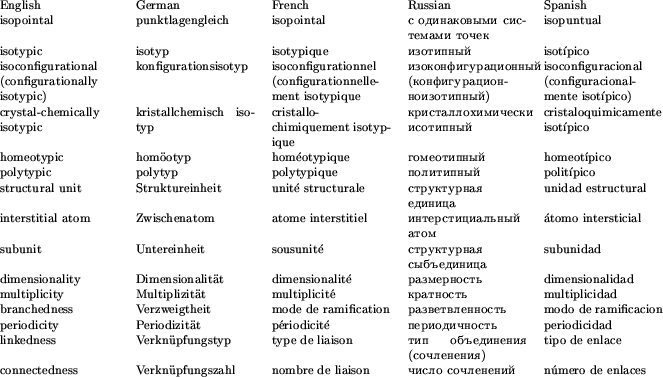
A glossary of the principal English, German, French, Russian and Spanish nomenclature terms used in this report is provided in Table 4 for the convenience of the reader.
Thiis Subcommittee has not considered certain aspects of the notation in detail, especially those which deal with very complex topics that are either not yet developed in sufficient detail or to which a number of different approaches exist. In order to assist the reader, the following reference list is given. Many citations contain further extensive reference lists.
Recombination structures
Hyde, Andersson, Bakker, Plug & O'Keeffe (1979); Makovicky (1981, 1985); Makovicky & Hyde (1981); Andersson (1983); Parthé, Chabot & Cenzual (1985).
Crystal-chemical formulae, dimensionality
Lima-de-Faria & Figueiredo (1976); Parthé (1980); Liebau (1982, 1985).
Multiplicity, branchedness, periodicity, linkedness, connectedness
Liebau (1982, 1985)
Condensation process
Lima-de-Faria & Figueiredo (1976, 1978); Hawthorne (1983).
Packing of structural units
Lima-de-Faria & Figueiredo (1976); Zvyagin (1987).
Layer description
Lima-de-Faria (1965); Lima-de-Faria & Figueiredo (1976); O'Keeffe & Hyde (1980); Hellner (1986); Smith & Dytrych (1986).
Bauverband approach
Hellner, Koch & Reinhardt (1981); Hellner & Sowa (1985); Hellner (1986).
The constructive criticism and encouragement of Dr. S. C. Abrahams and Professor Th. Hahn are gratefully acknowledged. Our work was made possible by the financial support of the following institutions: Instituto de Investigação Científica Tropical (Lisbon); Instituto Nacional de Investigação Científica (Lisbon); Calouste Gulbenkian Foundation (Lisbon); Stiftung Volkswagenwerk (Hannover); Commission Administrative, Université de Genève (Geneva); Danish Natural Science Research Council (Copenhagen).
References
ANDERSSON, S. (1983). Angew. Chem. 95, 67-80.
BOKII, G. B. (1954). Introduction to Crystal Chemistry. Moscow: Univ. Publ. House. (In Russian.) Engl. transl. by Joint Publ. Res. Service, New York (1960) (esp. pp. 192-199).
BRAGG, W. L. (1930). Z. Kristallogr. 74, 237-305.
BRUNNER, G. O. (1977). Acta Cryst. A33, 226-227.
BRUNNER, G. O. & SCHWARZENBACH, D. (1971). Z. Kristallogr. 133, 127- 133.
BRUZZONE, G., FORNASINI, M. L. & MERLO, F. (1970). J. Less-Common Met. 22, 253-264 (esp. p.260).
DONNAY, J. D. H., HELLNER, E. & NIGGLI, A. (1964). Z. Kristallogr. 120, 364-374.
FISCHER, W., KOCH, E. & HELLNER, E. (1971). N. Jahrb. Mineral. Monatsh. pp. 227-237.
FRANK, F. C. & KASPER, J. S. (1958). Acta Cryst. 11, 184-190.
FRANK, F. C. & KASPER, J. S. (1959). Acta Cryst. 12, 483-499.
GELATO, L. M. & PARTHÉ, E. (1987). J. Appl. Cryst. 20, 139-143.
GUINIER, A., BOKII, G. B., BOLL-BORNBERGER, K., COWLEY, J. M., DUROVIC, S., JAGODZINSKI, H., KRISHNA, P., DE WOLFF, P. M., ZVYAGIN, B. B., COX, D. E., GOODMAN, P., HAHN, TH., KUCHITSU, K. & ABRAHAMS, S. C. (1984). Acta Cryst. A40, 399-404.
HAWTHORNE, F. C. (1983). Acta Cryst. A39, 724-736.
HELLNER, E. (1965). Acta Cryst. 19, 703-712.
HELLNER, E. (1986). Z. Kristallogr. 175, 227-248.
HELLNER, E., KOCH, E. & REINHARDT, A. (1981). The Homogeneous Frameworks of the Cubic Crystal Structures. Physics Data, Vol. 16-3. Karlsruhe: Fachinformationszentrum.
HELLNER, E. & SOWA, H. (1985). The Cubic Structure Types Described in their Space Groups with the Aid of Frameworks. Physics Data, Vol. 16-3. Karlsruhe: Fachinformationzentrum.
HERMANN, C. (1960). Z. Kristallogr. 113, 142-154.
HOPPE, R. (1979). Z. Kristallogr. 150, 23-52.
HYDE, B. G., ANDERSSON, S., BAKKER, M., PLUG, C. M. & O'KEEFFE, M. (1979). Prog. Solid State Chem. 12, 273-327.
International Tables for Crystallography (1983). Vol. A, 1st ed. (2nd ed., 1987), edited by Th. Hahn. Dordrecht: Reidel. (Present distributor Kluwer Academic Publishers, Dordrecht.)
IUPAC (1990). Nomenclature of Inorganic Chemistry. Oxford: Blackwell.
LAVES, F. (1930). Z. Kristallogr. 73, 202-265, 275-324.
LAVES, F. (1980). Z. Kristallogr. 151, 21-29.
LIEBAU, F. (1982). Rev. Mineral. 5, 1-24.
LIEBAU, F. (1985). Structural Chemistry of Silicates. Structure, Bonding and Classification. Berlin: Springer, Russian ed. Strukturnaya Khimiya Silikatov. Moscow: Mir, 1988.
LIMA-DE-FARIA, J. (1965). Z. Kristallogr. 122, 346-358, 359-374.
LIMA-DE-FARIA, J. & FIGUEIREDO, M. O. (1976). J. Solid State Chem. 16, 7-20.
LIMA-DE-FARIA, J. & FIGUEIREDO, M. O. (1978). Garcia de Orta, Sér. Geol. 2, 69-76.
MACHATSCHKI, F. (1928). Centralbl. Miner. Geol. Paläont. Abt. A, pp. 97-104.
MACHATSCHKI, F. (1947). Monatsh. Chem. 77, 333-342.
MACHATSCHKI, F. (1953). Specielle Mineralogie auf geochemischer Grundlage (esp. pp. 298-353). Wien: Springer.
MAKOVICKY, E. (1981). Fortschr. Mineral. 59, 137-190.
MAKOVICKY, E. (1985). Fortschr. Mineral. 63, 45-89.
MAKOVICKY, E. & HYDE, B. G. (1981). Non-commensurate (Misfit) Layer Structures. In Structure and Bonding, Vol. 46, pp. 101-175. Berlin: Springer.
NIGGLI, P. (1919). Geometrische Kristallographie des Diskontinuums. Leipzig: Bornträger.
NIGGLI, P. (1945). Grundlagen der Stereochemie. Basel: Birkhäuser.
O'KEEFFE, M. (1979). Acta Cryst. A35, 772-775.
O'KEEFFE, M. & HYDE, B. G. (1980). Philos. Trans. R. Soc. London, 295, 553-623.
PARTHÉ, E. (1980). Acta Cryst. B36, 1-7.
PARTHÉ, E., CHABOT, B. A. & CENZUAL, K. (1985). Chimia, 39, 164- 174.
PARTHÉ, E. & GELATO, L. M. (1984). Acta Cryst. A40, 169-183.
SMITH, J. V. & DYTRYCH, W. J. (1986). Z. Kristallogr. 175, 31-36.
ZVYAGIN, B. B. (1987). Sov. Phys. Crystallogr. 32, 394-399.
- ...
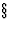 8.2.1)
8.2.1) - IT will henceforth denote International Tables for Crystallography, Vol. A, 1983 (first edition) and 1987 (second edition).
- ...orbits
- A crystallographic point configuration (or crystallographic orbit) (IT
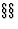 8.3.2 and 14.1) is an infinite set of points which is generated from one point by all symmetry operations of a given space group.
8.3.2 and 14.1) is an infinite set of points which is generated from one point by all symmetry operations of a given space group.
- ...states.
- The term isostructural is synonymous with isotypic. Isomorphy in its original definition meant close similarity of external crystal shape and analogy of chemical composition with the implication of close similarity of internal structure. Nowadays this term is used for a variety of different phenomena [series of crystal-chemical isotypes; solid-solution series (mixed crystals); atomic/ionic substitutions in crystal structures without regard to the existence or absence of isotypy]. Its use is not recommended.
- ...blocks,
- Blocks, rods and slabs are understood here as structure portions which are finite, or infinite in one or two dimensions, respectively.
- ...brackets.
-
The present proposal strongly advocates putting information on coordination numbers and coordination polyhedra in the form of trailing superscripts and not as subscripts as suggested by IUPAC (1990). Although all symbols proposed here could be used as subscripts, their juxtaposition with atomic proportions (especially fractional ones) can lead to confusion even in simple cases. For example:
K[6]Alo,2
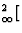 AltSit,3O10](OH) 2 (for muscovite) instead of K[6]Al
AltSit,3O10](OH) 2 (for muscovite) instead of K[6]Al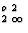 [AltSit 3O10](OH)2.
[AltSit 3O10](OH)2.The IUPAC system with its longer subscripts (tet for tetrahedral instead of t etc.) can be extended to more complicated cases only with difficulty (and ambiguity) and is inappropriate for irregular coordination that can only be expressed numerically, e.g. K[12]. The IUPAC proposal to indicate diferent types of coordination by parentheses has similar problems, since different types of brackets are used with meanings that differ from those in normal chemical formulae.
- ...atoms
- Henceforth the term 'atom' will be applied regardless of ionization state.
- ...symbols
- These pictorial symbols have already been used in Acta Cryst. (Parthé, 1980).
These pages are maintained by the Commission Last updated: 15 Oct 2021