4.69. XTINCT: Extinction from equivalent reflections

4.69.1. Introduction

The greater accuracy required for high precision density studies has led to the development of XTINCT. These studies require a particularly careful treatment of the correction factors for absorption and extinction, both of which depend on the size and shape of the crystal. Extinction coefficients determined from structure factor least squares processes (such as CRYLSQ) are approximate because of correlation with other intensity dependent errors.

XTINCT determines the isotropic extinction correction factor from the measured intensity variations of symmetrically equivalent reflections. This application relies on a non-spherical crystal in which the path lengths of symmetrically equivalent reflections are different. The precision of the method depends on several factors: the measured precision of the intensity data, the crystal shape (non-spherical but well-defined faces so that accurate path lengths can be calculated), the space group symmetry (the higher the better) and the extent of the data measured (a full sphere is highly desirable).

The correction for secondary (Type I) extinction is based on the theory of Zachariasen (1967) and the application procedure of Larson (1970). The corrected measured structure factor is F_m^(cor).

F_m ^(cor) = F_m/y^1/2

where

y = (1 + 2r^*|F_k|²Qg())^-1/2

and

Q = (e⁴/(m²c⁴V²)) (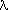³/sin2) ((p+(1-p)cos⁴2)/ (p+(1-p)cos²2))T

The function g() adapts the formalism to several special cases of extinction. This is necessary to ensure that the parameter r* is independent of scattering angle.

case 1 - Type II, primary extinction g() = sin2

case 2 - Type I, secondary extinction g() = 1

Parameter p specifies the fraction of total intensity incident on the crystal specimen, that is polarised perpendicularly to the diffraction plane of that specimen. In the instance of neutron diffraction Q reduces simply to

k²(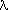³/(V²sin2))T ,

where the neutron scattering length k=10^-14m.

The secondary extinction coefficient r* is determined by minimising the statistical variation of the intensities for symmetry equivalent reflections. The minimum variance is found when the first derivative of the variance quadratic is zero. The derivative is taken with respect to the extinction parameter r*, which in the isotopic case is a scalar variable. In practice the quadratic is approximated by a Taylor expansion about r* truncated at the second order. The zero point of the first-order differential equation is found analytically using an iterative method which terminates when the shift in r* at each iteration becomes less than 0.0001 of (r*). The weighting of each set of equivalents is given by 1/² so that the stronger reflection intensities dominate the refinement. In accordance with the theory, the stronger reflections more accurately reflect the effect of extinction.

4.69.2. Application

XTINCT works best when applied to a full sphere of measured intensities. This provides as many equivalent reflections as possible. The strong dependence of the refinement on path length variations between equivalents restricts its application to non-spherical crystals. The procedure is applied after absorption corrections and applied to clustered F squared data.Here are the calculation steps needed for the application of XTINCT. This is when extinction is applied to |F|² data. See example 4 for a typical input file which parallels these steps.

1. A full sphere of intensity data should be collected from a single non-spherical crystal and processed with the STARTX and DIFDAT steps.

2. The intensity data is then processed using SORTRF aver 2to calculate the merge R-factor R_int. The output of this run is NOT saved.

3. The intensity data from (1) is then corrected for absorption using the program ABSORB. The tbar option must be set so that the mean path lengths of the individual reflections are stored on the bdf. An analytical absorption calculation is recommended for the most precise path lengths.

4. The output bdf from ABSORB is processed with SORTRF aver 2 to again calculate the merge R-factor R_int. The output of this run is NOT saved. This is to check the effect of the absorption corrections on the equivalent data.

5. The output bdf from ABSORB is processed with SORTRF clus to cluster equivalent reflections into sequential groups. sepfrl is required to group Friedels separately, if a non-centrosymmetric structure. This output is saved.

6. The clustered intensities from SORTRF are converted to structure factors squared with ADDREF nobay and reduce itof2.

7. Then use GENEV enot to determine the scale factor between observed and calculated structure factors. This is essential to place the extinction coefficient r* calculated in the next step on an absolute scale.

8. Apply the XTINCT program (a description of the input options is below).

9. Apply ADDREF nobay and reduce f2toi to convert the F squared to I.

10. Apply SORTRF aver 2 for the fourth time to yield the final R-factor R_int. This provides the final measure of the effect of correcting for extinction and absorption.

11. Finally apply ADDREF nobay and reduce itof to reduce the intensities to F.

4.69.3. XTINCT Options

In the default mode XTINCT calculates, refines and applies the extinction coefficient r* to the F² data. This data is output to the bdf along with the value of r* (on the absolute scale supplied from the prior GENEV run). 25 reflections will be printed.

Options on the XTINCT line and on the limits line provide for various controls on this calculation. The coefficient r* may be determined within specific regions of the data using the limits control line (though the resulting r* is then applied to all data). The value of r* may also be determined separately for each set of equivalents by entering the sall option (the resulting values are output to the PCH file). A value of r* may be input and applied using the appx option. Because sets of equivalent reflections with identical tbars can result in singularities, or negative r*, these sets are automatically skipped in the refinement. They may, however, be included using the incl option. Similarly, large anomalous dispersion difference between Friedel related reflections (for non-centrosymmetric spacegroups) can effect the refinement of r* and these will normally be treated separately, but will be treated as symmetrically equivalent reflections if the option eqfr is entered. The polarisation factor p, if unavailable on the bdf and not included as an option on the title line, takes the default value of unpolarised radiation (0.5).

4.69.4. File Assignments

• Reads reflection data from the input archive bdf.

• Outputs corrected (or uncorrected) data on the output archive bdf.

• Optionally outputs a pch file.

4.69.5. Examples

XTINCT

This is the standard run which refines and applies the extinction coefficient dat to the F² data. 25 reflections will be printed and the scaled r* value will be stored on the output bdf.

XTINCT print eqfr  
limits  f2rl 1000  100000

The extinction r* will be refined on all sets of equivalents for which the average F² lies between 1000 and 100000. All reflections will be printed, and the Friedel related intensities will be treated as equivalent reflections.

XTINCT  appx 153 22  print 40

The unscaled extinction correction r* of 153 and a sigma r* of 22 will be applied to the data. The first 40 reflections on the bdf will be printed.

SORTRF  aver 2 
end              : important - do not use a copybdf without preceding end 
copybdf b a   : <<<<<<<<<<<< do not save output bdf
ABSORB   analyt  scal 7604.19 irel tbar print 20       
diff    a a c a        
orient  2  0  0  29.91 27.79  0 2 0 331.86 99.84       
faceml -1  1  0  .00318                     
faceml  1 -1  0  .00318       
faceml  1  1  0  .00364        
faceml -1 -1  0  .00364        
faceml  0  0  1  .00635        
faceml  0  0 -1  .00635        
faceml -5 -8 -2  .00440        
faceml  5  0 -1  .00440        
SORTRF  aver 2
end              : important - do not use a copybdf without preceding end 
copybdf b a   : <<<<<<<<<<<<<<< do not save output bdf
SORTRF  clus        
ADDREF  nobay lpin       
reduce  itof2 rlp4       
bdfin   all
remove  f2rl sgf2       
GENEV   enot       
XTINCT  irel       
SORTRF  aver 2 print -9999       
ADDREF  nobay ffac        
reduce  itof       
bdfin   all

4.69.6. References

• Becker, P.J. Coppens, P. (1974) Acta Cryst A30, 129-147.

• Olthof-Hazekamp, R. (1991) Xtal3.4 Manual, CRYLSQ.

• Larson, A.C. (1970) p292 Crystallographic Computing: Munksgaard.

• Maslen, E.N. Spadaccini, N. (1992) Acta Cryst. A49, 661-667.

• Spadaccini, N. (1989) Proceedings of CRYSTAL XVI, Lorne SCA Meeting.

• Zachariasen, W. H. (1967) Acta Cryst 23, 558-564.