Projections of cubic crystals

Ian O. Angell and Moreton Moore

1. Introduction

Crystals are three-dimensional objects and are represented on paper by suitable projections. The use to which the resulting picture is to be put determines the choice of projection. Clinographic, orthographic and perspective projections are briefly described here, with examples taken from the cubic crystal system.

2. Clinographic, orthographic and perspective projections

Imagine one wishes to represent a cube on paper. There are six square faces but one cannot see them all at once (unless the cube is transparent!). The hidden edges may be included in the drawing to indicate their positions as if they were visible.

Only one face will be seen if the cube is viewed centrally and perpendicular to this face: not a very informative view if one wishes to obtain an overall impression of the object (which in this case might be a square prism). It is usual to arrange the viewpoint so that as many faces as possible are visible, or equivalently the object is turned so that this is the case.

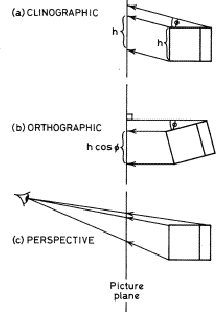
In the clinographic projection the cube is turned through an angle ( $\theta$ ) about a vertical axis, making both the front and right hand faces visible. The cube is then projected on to a vertical plane by parallel straight lines, which are inclined to the horizontal so that the top face is brought into view (Fig. ia).

**Figure i**
$\begin{figure} \includegraphics {figi.ps} \end{figure}$

The orthographic projection is also a parallel one, but here the projection lines meet the (vertical) plane at right angles. The cube is tilted forwards through an angle $\phi$ before projection to show the top face (Fig. ib). If the angle of tilt $\phi$ equals the angle that the projection lines make with the horizontal in the clinographic projection, then these clinographic and orthographic views are closely similar, (Fig. ii), but differ as follows. The vertical dimensions in the clinographic projection are magnified by the factor sec $\phi$ compared with the orthographic: or in other words, the height h of the crystal will be preserved in the clinographic projection, whereas in this orthographic projection it will appear as h cos $\phi$ .

In the standard setting of the crystal, $\phi$ is usually chosen to be 9 $^\circ$ 28 $^{\prime}$ so that its tangent is $\frac{1}{6}$ , for ease of drawing. sec $\phi$ is then ( $\sqrt{37}$ )/6 = 1.0138, and cos $\phi$ = 0.9864. The fact that these figures are very close to unity shows that these two views will be nearly the same. (In early books on mineralogy, tan $\phi$ was taken to be $\frac{1}{9}$ .) The angle $\theta$ about the vertical is usually chosen to be 18 $^\circ$ 26 $^{\prime}$ so that tan $\theta$ = $\frac{1}{3}$ . An orthographic projection which is closely similar to this clinographic standard is one projected along the direction which (in the cubic crystal system) has zone-axis symbol [621] (and appearing in the diagrams as 6.0 2.0 1.0: these are the components, referred to the cube, of a vector in this direction).

**Figure ii**
$\begin{figure} \includegraphics {figii.ps} \end{figure}$

Clinographic and orthographic projections are used widely in crystallography because parallel lines in the crystal project to parallel lines in the projections, and thus zonal relationships are preserved visually. The eye however sees things differently. A perspective view is a conical projection, with the apex of the cone at the eye. The picture plane is placed between the observer and the object: and parallel lines in space project to lines which converge to vanishing points on the picture plane.¹ The size of the picture will be determined not only by the size of the object but also by the relative distances of eye to picture plane and eye to object. Rear faces of the crystal will appear smaller than front faces because they are further away. In Fig. iic the viewpoint has coordinates (36, 12, 6) on an arbitrary scale, that is, the components are in the ratio 6:2:1, and so one is looking along the same direction as the [621] orthographic view. Perspective projections with slightly differing viewpoints, corresponding to the left and the right eye, may be used to construct stereoscopic pairs.

3. Cubic crystals

The variety of crystal shapes is so great that only crystals built up from cubes are considered in this pamphlet: other structural units have been omitted. Three mutually perpendicular crystallographic axes may be chosen parallel to the edges of the cubic unit cells. These are the familiar Cartesian axes Ox, Oy and Oz of coordinate geometry, where O is the origin. Their directions are represented by [100], [010] and [001]. Directions related by symmetry, such as these three, are written for brevity as $\langle$ 100 $\rangle$ . Other directions in the crystal may be referred to these axes; as in the earlier remark that the [621] direction has components in the ratios 6:2:1 along these three axes respectively.

A set of crystal faces, related to one another by symmetry, is called a form ; the symmetry being more obvious in specimens in which the faces are equally developed. For example, the cube, in the most symmetrical class, has three tetrad axes coinciding with the Ox, Oy and Oz axes, and three mirror planes perpendicular to these axes; four triad axes coinciding with the body diagonals $\langle$ 111 $\rangle$ ; six diad axes parallel to the face diagonals $\langle$ 110 $\rangle$ , and six mirror planes (making nine in all) perpendicular to these diad axes. The cube has a centre of symmetry. The underlying symmetry of crystals is much less obvious in specimens for which the faces of individual forms are unequally developed; but may still be deduced by considering the perpendiculars drawn to the faces from a point within the crystal, and their distribution in space. This is best done using a stereographic projection: the subject of another pamphlet².

**Figure iii** Rhombic dodecahedron made from cubes.
$\begin{figure} \includegraphics {figiii.ps} \end{figure}$

In the cubic crystal system there are five distinct classes or point groups : that is, five different combinations of symmetry elements, but all have in common the presence of four triad axes of symmetry. These are listed in Table 1. An axis of symmetry X perpendicular to a mirror plane m is written $\displaystyle\frac{\mbox{X}}{m}$ (or X/m ). The maximum symmetry of a cube, as described above, is represented by the point group symbol $\displaystyle\frac{4}{m} \overline{3} \frac{2}{m}$ (or 4/m $\overline{3}$ 3/m , often abbreviated to m 3 m ).

The orientation of a plane in crystallography is described in terms of its Miller indices . These are the reciprocals of the relative intercepts, in terms of unit cell edges, that the plane makes with the three crystallographic axes, expressed in whole numbers. In general, if the intercepts are a/h, b/k, c/l, where a, b and c are the cell edges, then the Miller indices of the plane are h, k, l, usually written (hkl). In the cubic crystal system, the unit cells are cubes, so a = b = c. (In the drawings here a = 1.) The face of the cube, perpendicular to the [100] direction (i.e. to the Ox Cartesian axis) has Miller indices (100), since the intercepts on the three axes are a/1, a/0, a/0: the latter two intercepts (on Oy and Oz), being at infinity. (For cubic crystals, the [hkl] direction is perpendicular to the (hkl) plane, but this is not so for crystals of other crystal systems.) The faces of an octahedron make equal intercepts, positive and negative, on all three axes and therefore have Miller indices (111), ( $\overline{1}$ 11), (1 $\overline{1}$ 1), (11 $\overline{1}$ ), ( $\overline{111}$ ), (1 $\overline{11}$ ), ( $\overline{1}$ 1 $\overline{1}$ ) and ( $\overline{11}$ 1). The minus signs are written above the symbols for compactness. All eight symmetrically related faces of the form are written as $\{$ 111 $\}$ .

**Table 1:** Cubic crystal classes or point groups

Full symbol	Abbreviated symbol		Symmetry elements along the directions

		$\langle$ 100 $\rangle$	$\langle$ 111 $\rangle$	$\langle$ 110 $\rangle$

$\displaystyle\frac{4}{m}\,\=3\,\frac{2}{m}$	$m\,3\,m$	4-fold axes perpendicular to mirror planes	3-fold rotation-inversion axes	2-fold axes perpendicular to mirror planes
$4\,3\,2$	$4\,3$	4-fold axes	3-fold axes	2-fold axes
$\=4\,3\,m$	$\=4\,3\,m$	4-fold rotation-inversion axes	3-fold axes	mirror planes perpendicular to these directions
$\displaystyle\frac{2}{m}\,\=3$	$m\,3$	2-fold axes perpendicular to mirror planes	3-fold rotation-inversion axes	-
$2\,3$	$2\,3$	2-fold axes	3-fold axes	-

4. The diagrams

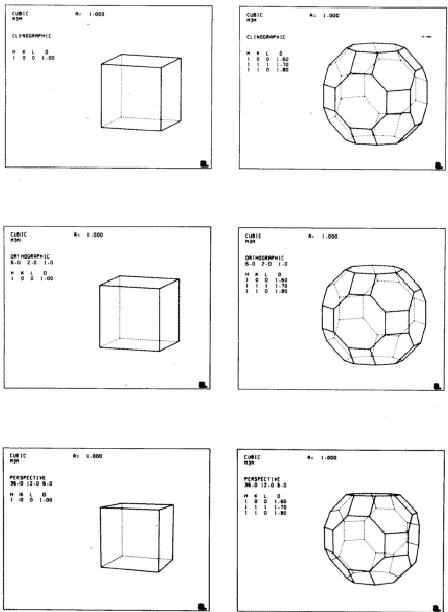
In each computer drawn diagram, the Miller indices of the face(s) defining the form(s) are shown under the letters H, K, L (printed by the computer as capital letters). The distance of this face from the centre, on an arbitrary scale, is shown under D. The point group symmetry (shown at the top of each diagram under the word CUBIC) then operates on the specified face (or faces) to give the complete solid. For example, m 3 m symmetry generates all six faces of the cube from the single face (100). For the solids thus generated from a single face, four orthographic views are given with hidden edges omitted: a `general' view along the [621] axis, closely similar to a standard clinographic projection; and views along the [100], [110] and [111] directions. For each cubic crystal viewed along the [111] direction the three-fold symmetry is evident. There are three other equivalent three-fold axes along [1 $\overline{11}$ ], [ $\overline{1}$ 1 $\overline{1}$ ] and [ $\overline{11}$ 1]. One can also see immediately whether the crystal possesses a four-fold axis along [100], a diad axis along [110], or mirror planes bisecting any of the projections along [100], [110], and [111].

As far as possible, similarly shaped solids are placed together in the pages which follow. In some cases two different settings (`positive' and `negative') are given for the same crystal: (3 & 4, 9 & 10, 15 & 16, 19 & 20, 25 & 26); and some crystals are mirror images (enantiomorphs) of one another: (22 & 23, 27 & 28).

Table 2 lists the names of the crystal forms and table 3 shows their distribution amongst the five cubic point groups, or crystal classes.

The cube (no. 1) appears in all five columns because any one of the cubic point group symmetries operating on the (100) plane will generate all six faces of the cube. The rhombic dodecahedron (5) also appears five times for the same reason; whilst the octahedron (2) appears three times, and the tetrahedron (3) twice. $\{$ 210 $\}$ , $\{$ 310 $\}$ and $\{$ 320 $\}$ are particular examples of $\{h k 0\}$ ; $\{$ 211 $\}$ and $\{$ 311 $\}$ of $\{$ hll $\}$ with h > l ; and $\{$ 221 $\}$ is an example of $\{$ h h l $\}$ with h > l . $\{$ 321 $\}$ is a particular case of the general form $\{hkl\}$ in which all the indices are different and non-zero. In table 3, it will be seen, for example, that the same crystal form (15) will be generated either by $\overline{4}$ 3 m or by 23 operating on (211).

Very often crystals exhibit faces of more than one form together. Some examples of combinations of two forms are shown here. The overall shape of a crystal is very much determined by the relative distances from the centre of the two kinds of face: one dominant form perhaps being only slightly modified by another. The drawings are still of ideal crystals, in which all faces of each form have the same size and shape. Real crystals seldom have the faces of forms so uniformly developed.

Graphical index

**Table 2:** Cubic crystal forms: key to the figure numbers
Fig. No.	Form	(Maximum) Symmetry	Name	No. of faces
1	$\{$ 100 $\}$	m 3 m	Cube	6
2	$\{$ 111 $\}$	m 3 m	Octahedron	8
3	$\{$ 111 $\}$	$\=4 3 m$	Tetrahedron (positive)	4
4	$\{1\=11\}$	$\=4 3 m$	Tetrahedron (negative)	4
5	$\{$ 110 $\}$	m 3 m	Rhombic dodecahedron	12
6	$\{$ 210 $\}$	m 3 m	Tetrahexahedra	24
7	$\{$ 310 $\}$
8	$\{$ 320 $\}$
9	$\{$ 210 $\}$	m 3	Pentagonal dodecahedra (or pyritohedra)	12
10	$\{$ 120 $\}$
11	$\{$ 310 $\}$
12	$\{$ 320 $\}$
13	$\{$ 211 $\}$	m 3 m	Icositetrahedra (or trapezohedra)	24
14	$\{$ 311 $\}$	m 3 m
15	$\{$ 211 $\}$	$\=4 3 m$	Tristetrahedra	12
16	$\{2\=11\}$
17	$\{$ 311 $\}$
18	$\{$ 221 $\}$	m 3 m	Trisoctahedron	24
19	$\{$ 221 $\}$	$\=4 3 m$	Deltoid dodecahedron (or deltohedron)	12
20	$\{2\=21\}$	$\=4 3 m$
21	$\{$ 321 $\}$	m 3 m	Hexoctahedron	48
22	$\{$ 321 $\}$	4 3	Pentagonal icositetrahedra (or gyroids)
23	$\{$ 312 $\}$	4 3		24
24	$\{$ 321 $\}$	$\=4 3 m$	Hexatetrahedron	24
25	$\{$ 321 $\}$	m 3	Didodecahedron (or diploid)
26	$\{$ 312 $\}$	m 3		24
27	$\{$ 321 $\}$	2 3	Tetrahedral pentagonal dodecahedra
28	$\{$ 312 $\}$	2 3	(or tetartoids)	12

(The figures continue unnumbered for the combinations of forms.)
(29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40)

**Table 3:** Distribution of crystal forms amongst the five cubic classes
	m 3 m	4 3	$\=4 3 m$	m 3	2 3
$\{$ 100 $\}$	1	1	1	1	1
$\{$ 110 $\}$	5	5	5	5	5
$\{$ 111 $\}$	2	2	3	2	3
$\{$ hk0 $\}$	6	6	6	9	9
$\{$ hll $\}$ h > l	13	13	15	13	15
$\{$ hhl $\}$ h > l	18	18	19	18	19
$\{$ h k l $\}$	21	22	24	25	27

The numbers are figure numbers. See Table 2 for the names of the forms.

Acknowledgements

The authors would like to thank Dr A. F. Seager and Dr E. J. W. Whittaker for helpful comments on the manuscript.

Crystallography Matters!