Close-packed structures
P. Krishna and D. Pandey
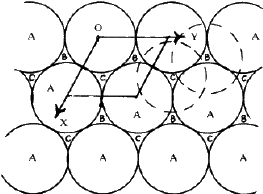
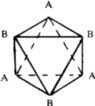
The crystal structures of a large number of metals, alloys and inoganic compounds can be described geometrically in terms of a close-packing of equal spheres, held together by interatomic forces. Frequently, the positions of one kind of atoms of ions in inorganic structures correspond approximately to those of equal spheres in a close-packing with the other atoms distributed among the voids. All such structures will be referred to as close-packed structures though they may not be ideally close-packed. The close-packed arrangement of equal spheres in a plane is shown in Fig. 1 where each sphere is in contact with six other spheres. Since the symmetry of this layer is 6mm , such a layer is called a hexagonal close-packed layer. Let this layer be called an A layer. It contains two types of triangular voids, one with the apex of the triangle upwards in the diagram and labelled B, and the other with the apex downwards and labelled C. In the two-dimensional unit cell indicated in the figure (a=b, ![]() =120
=120![]() ) the three positions, A, B and C have coordinates 00,
) the three positions, A, B and C have coordinates 00, ![]()
![]() and
and ![]()
![]() .
.
In a three-dimensional packing the next hexagonal close-packed layer of spheres can occupy either the sites B or C, but not both. Similarly the layer above a B layer can be either C or A and that above a C layer either A or B. No two successive layers can be alike. The positions B and C are displaced with respect to A by vectors +S and -S respectively where S = a/3 ![]()
![]() 010
010![]() in the Miller-Bravais notation.
in the Miller-Bravais notation.
Any sequence of the letters, A. B and C with no two successive letters alike represents a possible manner of close-packing equal spheres. In such a three- dimensional close-packing, each sphere is surrounded by and touches 12 other spheres. This is the maximum number of spheres that can be arranged to touch a given sphere and it provides the maximum packing density for an infinite lattice arrangement. (There are however other arrangements of a finite number of equal spheres which have a higher packing density1.) It is evident from the foregoing that the number of different close-packed structures that are possible in three dimensions is infinite. The identity period or c dimension of the hexagonal unit cell in a three-dimensional close-packed structure is determined by the number of layers after which the stacking sequences repeats itself. The two most common close-packed structures which occur in nature are: (i) the hexagonal close-packing (hcp) with a layer stacking ABAB.. and (ii) the cubic close-packing (ccp) with a layer stacking ABCABC.. They have identity periods of two and three layers respectively. In addition to the hcp and ccp modifications, a number of materials, like SiC, ZnS, CdI2, PbI2, AgI and GaSe are known2,3,4 to crystallize in a large variety of close-packed structures, called polytypes, with larger identity periods. The different polytype structures of the same material have identical a and b dimensions of their hexagonal unit cell but differ along c . Even for the same identity period of n layers, a number of different close-packed structures are possible with different arrangements of the n layers. The extent to which a real crystal structure approximates to a close- packing can be determined from the h /a ratio, where h is the separation between successive close-packed layers and a is the diameter of the spheres. For an ideally close-packed structure, this ratio must be ![]() = 0.81652,5. Table 1 lists the h /a ratio for some metals and inorganic materials with hcp structure.
= 0.81652,5. Table 1 lists the h /a ratio for some metals and inorganic materials with hcp structure.
| Material | h/a | Material | h/a |
| Cd | 0.943 | AgI | 0.815 |
| Zn | 0.928 | BeO | 0.815 |
| He | 0.8165 | CdSe | 0.815 |
| Co | 0.814 | ZnO | 0.800 |
| Mg | 0.812 | AlN | 0.800 |
| Sc | 0.797 | CdS | 0.810 |
Voids in a close-packing
In case of close-packed inorganic compounds, the larger atoms or ions occupy positions approximately corresponding to those of equal spheres in a close- packing while the smaller atoms are distributed among the voids. Three- dimensional close-packings of spheres have two kinds of voids:
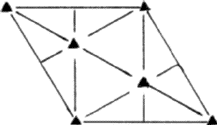
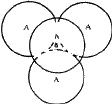
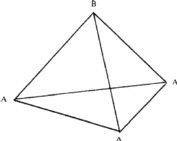
(i) If the triangular void in a close-packed layer has a sphere directly over it, there results a void with four spheres around it, as shown in Fig. 2a. Such a void is called a tetrahedral void since the four spheres surrounding it are arranged on the corners of a regular tetrahedron (Fig. 2b). If R denotes the radius of the four spheres surrounding a tetrahedral void, the radius of the spheres that would just fit into this void is given2,5 by 0.225 R.
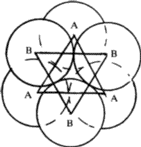
(ii) If a triangular void pointing up in one close-packed layer is covered by a triangular void pointing down in the adjacent layer, then a void surrounded by six spheres results (Fig. 2c). Such a void is called an octahedral void since the six spheres surrounding it lie at the corners of a regular octahedron (Fig. 2d). The radius of the sphere that would just fit into an octahedral void in a close-packing is given2,5 by 0.414 R.
| (a):Tetrahedral void | (b): Tetrahedron |
 |
 |
| (c): Octahedral void | (d): Octahedron formed by the centres of squares |
 |
 |
To determine the number of tetrahedral and octahedral voids in a three-dimensional close-packing of spheres, we note that a sphere in a hexagonal close-packed layer A is surrounded by three B voids and three C voids (Fig. 1). When the next layer is placed on top of this, the three voids of one kind (say B) are occupied and the other three (say C) are not. Thus the three B voids become tetrahedral voids and the three C voids become octahedral voids. A single sphere in a three-dimensional close-packing will have similar voids on the lower side as well. In addition, the particular sphere being considered covers a triangular void in the layer above it and another in the layer below it. Thus two more tetrahedral voids surround the spheres. This results in 2 ![]() 3 + 1 + 1 = 8 tetrahedral voids and 2
3 + 1 + 1 = 8 tetrahedral voids and 2 ![]() 3 = 6 octahedral voids surrounding the sphere. Since a tetrahedral void is shared by four spheres, there are twice as many tetrahedral voids as there are spheres. Similarly, since an octahedral void is surrounded by six spheres, there are as many octahedral voids as there are spheres.
3 = 6 octahedral voids surrounding the sphere. Since a tetrahedral void is shared by four spheres, there are twice as many tetrahedral voids as there are spheres. Similarly, since an octahedral void is surrounded by six spheres, there are as many octahedral voids as there are spheres.
In an actual crystal structure a particular atom can best fit into one or the other kind of void depending on its size relative to that of the close-packed atoms. Thus the radius ratio of the atoms present in a crystal imposes limitations on the coordination that they can have in real structures. Conversely, the coordination number of an atom imposes a limitation on the radius ratio. In effect this means that the size and coordination number of a central atom may require that its close-packed neighbours do not touch each other.
Symmetry and space group of close-packed structures
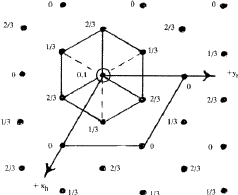
The symmetry of a single close-packed layer of spheres is 6mm . It has 2- , 3- and 6- fold axes of rotation normal to its plane as shown in Fig. 3. In addition it has three symmetry planes--one perpendicular to the x -axis, one perpendicular to the y axis and the third equally inclined to x and y . When two or more layers are stacked over each other in a close-packing the resulting structure retains all the three symmetry planes and has at least 3-fold axes parallel to [00.1] through the points 000, ![]()
![]() 0 and
0 and ![]()
![]() 0 as shown in Fig. 4. Such a structure belongs to the trigonal system and has a space group P3m1 or R3m1, according as the lattice is hexagonal or rhombohedral. This represents the lowest symmetry of a close-packing of spheres comprised of a completely arbitrary periodic stacking sequence of close-packed layers. If the arbitrariness in stacking successive layers in the unit cell is limited then higher symmetries can also result. It can be shown2,6 that it is possible to have three additional symmetry elements, namely, a centre of symmetry (
0 as shown in Fig. 4. Such a structure belongs to the trigonal system and has a space group P3m1 or R3m1, according as the lattice is hexagonal or rhombohedral. This represents the lowest symmetry of a close-packing of spheres comprised of a completely arbitrary periodic stacking sequence of close-packed layers. If the arbitrariness in stacking successive layers in the unit cell is limited then higher symmetries can also result. It can be shown2,6 that it is possible to have three additional symmetry elements, namely, a centre of symmetry (![]() , a mirror plane perpendicular to [00.1], and a screw axis 63. It was shown by Belov7 that consistent combinations of these symmetry elements can give rise to only eight possible space groups:
, a mirror plane perpendicular to [00.1], and a screw axis 63. It was shown by Belov7 that consistent combinations of these symmetry elements can give rise to only eight possible space groups:
P3m1, ![]() ,
, ![]() , P63mc
, P63mc
P63/mmc, R3m, ![]() and
and ![]()
Possible lattice types
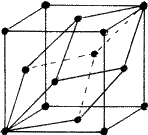
Close-packing of equal spheres can belong to the trigonal, hexagonal or cubic crystal systems. When the structure has the minimum symmetry discussed earlier it belongs to the trigonal system. When it has a 63 axis of symmetry it belongs to the hexagonal system. Structures belonging to the hexagonal system necessarily have a hexagonal lattice, i.e. a lattice in which we can choose a primitive unit cell with a = b ![]() c,
c, ![]() =
= ![]() = 90
= 90![]() , in Fig. 5. It should be noted that there are two spheres associated with each lattice point in the hcp structure, one at 000 and the other at
, in Fig. 5. It should be noted that there are two spheres associated with each lattice point in the hcp structure, one at 000 and the other at ![]()
![]()
![]() . Structures belonging to the trigonal system can have either a hexagonal or a rhombohedral lattice. By a rhombohedral lattice is meant a lattice in which we can choose a primitive unit cell with a = b = c,
. Structures belonging to the trigonal system can have either a hexagonal or a rhombohedral lattice. By a rhombohedral lattice is meant a lattice in which we can choose a primitive unit cell with a = b = c, ![]() =
= ![]() =
= ![]()
![]() 90
90![]() . Both types of lattices can be referred to either hexagonal or rhombohedral axes, the unit cell being non-primitive when a hexagonal lattice is referred to rhombohedral axes or vice versa.
. Both types of lattices can be referred to either hexagonal or rhombohedral axes, the unit cell being non-primitive when a hexagonal lattice is referred to rhombohedral axes or vice versa.
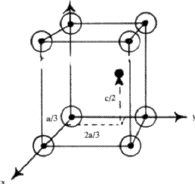
Figure 6 shows a rhombohedral lattice in which the primitive cell is defined by the rhombohedral axes a1, a2, a3; but a non-primitive hexagonal unit cell can be chosen by adopting the axes A1, A2, C. The latter has lattice points at 000.,
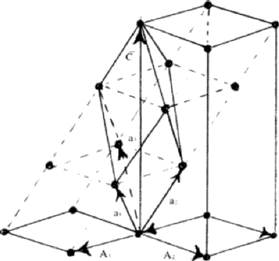 |
 |
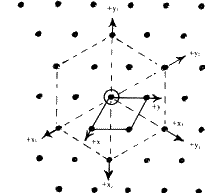
In close-packed structures, it is generally convenient to refer both hexagonal and rhombohedral lattices to hexagonal axes. The projection of the hexagonal lattice on the (001) plane is shown in Fig. 8. The axes, x, y define the smallest hexagonal unit cell, the z axis being normal to the plane of the paper; the hexagonal unit cell is primitive with all the lattice points at 000. Figure 9 depicts the projection of a rhombohedral lattice on the (00.1) plane. The full lines Oxh, Oyh represent the hexagonal axes and the three dotted lines represent rhombohedral axes. It is evident from the figure that the hexagonal unit cell of a rhombohedral lattice is non-primitive with lattice points at 000, ![]()
![]()
![]() and
and ![]()
![]()
![]() . If the lattice is rotated through 60
. If the lattice is rotated through 60![]() around [001], the hexagonal unit cell will then be centred at
around [001], the hexagonal unit cell will then be centred at ![]()
![]()
![]() and
and ![]()
![]()
![]() . These two settings of the rhombohedral lattice are called 'obverse' and 'reverse' settings. They are indistinguishable by X-ray methods since the two are crystallographically equivalent: they represent twin arrangements when both of them occur in the same single crystal.
. These two settings of the rhombohedral lattice are called 'obverse' and 'reverse' settings. They are indistinguishable by X-ray methods since the two are crystallographically equivalent: they represent twin arrangements when both of them occur in the same single crystal.
 |
 |
Notations used for representing close-packed structures
The special notations employed to distinguish the different close-packed structures of a material have been described in detail by Verma and Krishna2. In this section a brief description of only those notations which are more commonly used is given.
(a) Ramsdell's notation8
Close-packed structures can be designated by specifying the total number of layers in the hexagonal unit cell followed by the letter H , R or C to indicate the lattice type. Thus a symbol nH represents a structure with n layers in the primitive hexagonal unit cell while mR denotes a structure whose primitive lattice is rhombohedral and contains m layers in its hexagonal unit cell. In order to distinguish structures with same lattice type as well as the same repeat period along c , subscripts a , b , c or 1, 2, 3 are often used. This notation is applicable to all close-packed structures but it does not reveal the actual arrangement of the layers in the unit cell.
(b) The classical ABC notation
As pointed out earlier, the actual arrangement of layers in all close-packed structures can be described in terms of the ABC notation for close-packing of spheres. Thus the SiC type 6H has six Si and six C layers in its hexagonal unit cell stacked as A![]() B
B![]() C
C![]() A
A![]() C
C![]() B
B![]() where the Roman letters denote positions of layers of Si atoms and the Greek letters those of C atoms. Since the positions of C atoms are fixed relative to the positions of Si atoms it is customary to omit the Greek letters and write the structure as ABCACB. In the case of CdI2 structures, where the Cd atoms lie in the octahedral voids between alternate close-packed iodine layers, one often retains the Greek letters to denote the positions of Cd layers. Thus CdI2 type 4H has a structure A
where the Roman letters denote positions of layers of Si atoms and the Greek letters those of C atoms. Since the positions of C atoms are fixed relative to the positions of Si atoms it is customary to omit the Greek letters and write the structure as ABCACB. In the case of CdI2 structures, where the Cd atoms lie in the octahedral voids between alternate close-packed iodine layers, one often retains the Greek letters to denote the positions of Cd layers. Thus CdI2 type 4H has a structure A![]() B C
B C![]() B. While this notation gives a complete description of the structure it does not reveal the symmetry or lattice type directly and becomes cumbersome for structures with large repeat periods.
B. While this notation gives a complete description of the structure it does not reveal the symmetry or lattice type directly and becomes cumbersome for structures with large repeat periods.
(c) Zhdanov notation
If the layers in a close-packed structure are projected on to one of the close- packed planes, the atoms fall into one of the three possible positions A, B and C with xy coordinates 00, ![]()
![]() and
and ![]()
![]() respectively. The passage from A
respectively. The passage from A![]() B
B![]() C
C![]() A involves a vector translation of
A involves a vector translation of ![]()
![]() in the basal plane, whereas the passage from A
in the basal plane, whereas the passage from A![]() C
C![]() B
B![]() A involves a vector translation of
A involves a vector translation of ![]() ,
, ![]() =
= ![]() ,
, ![]() (fig. 1). H
(fig. 1). H![]() gg9 therefore denoted the former by a plus sign (+) and the latter by a minus sign (-). A structure such as ABCB is thus represented as ++--. The relationship between the three orientations, A, B and C of the close-packed layers may also be visualized in terms of clockwise or anticlockwise rotation about [00.1] through 60
gg9 therefore denoted the former by a plus sign (+) and the latter by a minus sign (-). A structure such as ABCB is thus represented as ++--. The relationship between the three orientations, A, B and C of the close-packed layers may also be visualized in terms of clockwise or anticlockwise rotation about [00.1] through 60![]() . Frank10 used the symbols
. Frank10 used the symbols ![]() and
and ![]() for the two rotations. Thus the
for the two rotations. Thus the ![]() symbol implies a cyclic change A
symbol implies a cyclic change A![]() B
B![]() C
C![]() A and the symbol
A and the symbol ![]() implies an anticyclic change. No compactness results from the use of these + and - or
implies an anticyclic change. No compactness results from the use of these + and - or ![]() and
and ![]() symbols for representing a close-packed structure because their number remains the same as the number of layers in the ABC sequence of the structure. Zhdanov11 therefore suggested summing up the consecutive + (or
symbols for representing a close-packed structure because their number remains the same as the number of layers in the ABC sequence of the structure. Zhdanov11 therefore suggested summing up the consecutive + (or ![]() ) and - (or
) and - (or ![]() ) signs and putting them down in numeral figures. Thus the 6H SiC structure having the ABC sequence ABCACB and a H
) signs and putting them down in numeral figures. Thus the 6H SiC structure having the ABC sequence ABCACB and a H![]() gg9 sequence +++-- is denoted by the symbol (33) in the Zhdanov notation.
gg9 sequence +++-- is denoted by the symbol (33) in the Zhdanov notation.
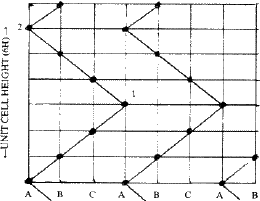
Ramsdell8 interpreted the Zhdanov symbols in terms of the zig-zag sequence of Si and C atoms in the (11![]() 0) planes of SiC structure. These planes contain all the atoms of the structure since the three symmetry axes parallel to [001] all lie in this plane. Figure 10 illustrates the meaning of the zig-zag sequence, taking the 6H (33) structure of SiC as example. If a Si or C atom lies on A in one layer, the next must be either to the right on B, or to the left on C. If to the right, the third layer may have its atom continue to the right or it may change direction and go to the left. Because of these repeated changes, a zig-zag pattern results. Such an arrangement can be described in terms of the number of layers added in each direction in succession and has been called the 'zigzag sequence' by Ramsdell. The unit cell is completed after arriving at an identical atom having the same environment as the atom from which one started. Thus in Fig. 10 the unit-cell of 6H is completed at 2 and not at 1. The Zhdanov notation is by far the most convenient and concise notation to describe close-packed structures.
0) planes of SiC structure. These planes contain all the atoms of the structure since the three symmetry axes parallel to [001] all lie in this plane. Figure 10 illustrates the meaning of the zig-zag sequence, taking the 6H (33) structure of SiC as example. If a Si or C atom lies on A in one layer, the next must be either to the right on B, or to the left on C. If to the right, the third layer may have its atom continue to the right or it may change direction and go to the left. Because of these repeated changes, a zig-zag pattern results. Such an arrangement can be described in terms of the number of layers added in each direction in succession and has been called the 'zigzag sequence' by Ramsdell. The unit cell is completed after arriving at an identical atom having the same environment as the atom from which one started. Thus in Fig. 10 the unit-cell of 6H is completed at 2 and not at 1. The Zhdanov notation is by far the most convenient and concise notation to describe close-packed structures.
(d) The h-c notation
In the h-c notation, used by Pauling12, Wyckoff13 and Jagodzinski14, one specifies each layer in terms of the orientation of layers above and below it. A layer is said to be in hexagonal configuration and is denoted as 'h' if it is surrounded on either side by layers in similar orientations. A layer is said to be in cubic configuration and is denoted as 'c' if it is surrounded on either side by layers in different orientations. Thus the 6H SiC structure with stacking sequence ABCACB can be written as hcchcc in the h-c notation. This notation is specially useful in dealing with X-ray diffraction effects from faulted structures and for calculating stacking fault energies15.
It is quite easy to transform from one notation to another. For this it is convenient to write first the complete ABC sequence of the structure and then express this in the desired notation. Some close-packed structures expressed in different notations are listed in Table 2.
| Ramsdell notation | ABC sequence | Zhdanov number | h-c notation |
| 2H | AB | (11) | h |
| 3C | ABC | c | |
| 4H | ABCB | (22) | hc |
| 6H 1 | ABCACB | (33) | hcc |
| 6H 2 | ABCBAB | (2211) | hchchh |
| 9R | ABACACBCB | (12) | hhc |
Examples of some close-packed structures
(i) Elements
The structure of many of the metallic and non-metallic elements can be described in terms of a close packing of equal spheres. There is a clear relationship between the structure and the position of an element in the Periodic Table. Elements in the same group tend to have the same structure at room temperature; for example, the alkali metals and Be, Mg, Zn and Cd (group IIA and IIB) are hcp; Cu, Ag and Au (group IB) are ccp. The elements of the rare-earth series crystallize in the ccp structure, the hcp structure or the 4H (ABCB) structure (e.g. Sm). The stable modification of Co at room temperature is probably hcp but it undergoes transformation to a ccp structure at high temperature.
(ii) Inorganic compounds
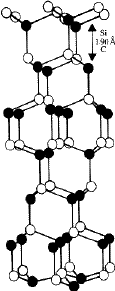
(a) Silicon carbide and zinc sulphide
SiC has a binary tetrahedral structure in which the Si and C layers are stacked alternately, each carbon layer occupying half the tetrahedral voids between successive close-packed silicon layers. One can regard the structure as consisting of two identical interpenetrating close-packings, one of Si and the other of C, with the one displaced relative to the other along the c -axis through one fourth of the layer spacing. The binding between Si and C atoms in SiC is predominantly covalent. The silicon-carbon bond length of 1.94 Å as calculated from the known covalent tetrahedral radii of C and Si is nearly equal to the observed silicon-carbon bond length of 1.89 Å. The tetrahedral arrangement of Si and C in SiC does not permit either a centre of symmetry (![]() ) or a plane of symmetry (m ) perpendicular to [00.1]. Silicon carbide can therefore have only four possible space groups -- P 3m 1, R 3m 1, P 63mc and F
) or a plane of symmetry (m ) perpendicular to [00.1]. Silicon carbide can therefore have only four possible space groups -- P 3m 1, R 3m 1, P 63mc and F ![]() 3m.
3m.
 |
Commercial SiC crystals are grown at temperatures above 2000![]() C and are called
C and are called ![]() -SiC crystals. The more common modifications in the
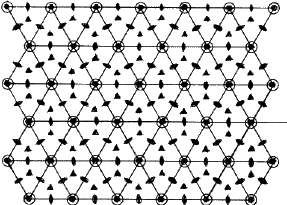
-SiC crystals. The more common modifications in the ![]() -SiC crystals are 6H , 15R and 4H . They have stacking sequences /ABCACB/ (=6H ), /ABCBACABACBCACB/(=15R ) and /ABCB/...(4H ). Figure 11 depicts the structure of the most common
-SiC crystals are 6H , 15R and 4H . They have stacking sequences /ABCACB/ (=6H ), /ABCBACABACBCACB/(=15R ) and /ABCB/...(4H ). Figure 11 depicts the structure of the most common ![]() -SiC modification 6H with a packing ABCACB. In addition to the common modications (often called the 'basic structures' of
-SiC modification 6H with a packing ABCACB. In addition to the common modications (often called the 'basic structures' of ![]() -SiC) several polytype structures with stacking sequences of larger repeat periods have been discovered. These have either a hexagonal or a rhombohedral lattice2. Table 3 lists the known structures of SiC. In all these structures the h/a ratio is 0.817, which is very close to the value of 0.8165 for an ideal close-packing. The cubic or
-SiC) several polytype structures with stacking sequences of larger repeat periods have been discovered. These have either a hexagonal or a rhombohedral lattice2. Table 3 lists the known structures of SiC. In all these structures the h/a ratio is 0.817, which is very close to the value of 0.8165 for an ideal close-packing. The cubic or ![]() -SiC, with a packing /ABC/ABC/..., is denoted as 3C and normally forms2 at temperatures below 1800
-SiC, with a packing /ABC/ABC/..., is denoted as 3C and normally forms2 at temperatures below 1800![]() C. It is regarded as the low- temperature modification of SiC and undergoes a solid-state transformation to the 6H structure at temperatures above 1800
C. It is regarded as the low- temperature modification of SiC and undergoes a solid-state transformation to the 6H structure at temperatures above 1800![]() C2,16,17. The wurtzite (2H ) modification of SiC, with a stacking sequence /AB/AB/..., does not occur in commercial SiC and has been synthesized by special methods between the temperatures of 1400 and 1500
C2,16,17. The wurtzite (2H ) modification of SiC, with a stacking sequence /AB/AB/..., does not occur in commercial SiC and has been synthesized by special methods between the temperatures of 1400 and 1500![]() C18. It is regarded as a metastable modification of SiC and undergoes solid-state transformation to the 3C and 6H structures at temperatures above 1400
C18. It is regarded as a metastable modification of SiC and undergoes solid-state transformation to the 3C and 6H structures at temperatures above 1400![]() C17. The h/a ratio in this structure is 0.8205 which differs considerably from the ideal h/a ratio for perfect close-packing.
C17. The h/a ratio in this structure is 0.8205 which differs considerably from the ideal h/a ratio for perfect close-packing.
| Polytype | Structure (Zhdanov sequence) | Polytype | Structure (Zhdanov sequence) |
| 2H | 11 | 54H | (33)6323334 |
| 3C | 57H | (23)93333 | |
| 4H | 22 | 57R | (33)234 |
| 6H | 33 | 69R 1 | (33)332 |
| 8H | 44 | 69R 2 | 33322334 |
| 10H | 3322 | 75R 1 | (33)334 |
| 14H | (22)233 | 75R 2 | (32)3(23)2 |
| 15R | 23 | 81H | (33)535(33)634 |
| 16H 1 | (33)222 | 84R | (33)3(32)2 |
| 16H 2 | 332332 | 87R | (33)432 |
| 18H | (22)333 | 90R | (23)43322 |
| 19H | (23)322 | 96R | (33)33434 |
| 20H | (22)344 | 99R | (33)43222 |
| 21H | 333534 | 105R | (33)532 |
| 21R | 34 | 111R | (33)534 |
| 24R | 35 | 120R | (22)523222333 |
| 27H | (33)2(23)3 | 123R | (33)632 |
| 27R | 2223 | 141R | (33)732 |
| 33R | 3332 | 147R | (3332)432 |
| 33H 1 | (33)2353334 | 159R | (33)832 |
| 33H 2 | (33)3(23)3 | 168R | (23)1033 |
| 36H 1 | (33)232(33)234 | 174R | (33)66(33)54 |
| 36H 2 | (33)43234 | 189R | (34)843 |
| 39H | (33)232(33)3(32)2 | 222R | (33)634(33)434 |
| 39R | 3334 | 267R | (23)1722 |
| 45R | 232332 | 273R | (23)1733 |
| 51R 1 | (33)232 | 303R | (33)1632 |
| 51R 2 | (22)323 | 393R | (33)2132 |
The structure of ZnS is analogous to that of SiC. The bonding in ZnS is known to be partly ionic and partly covalent. The wurtzite and sphalerite modifications of this compound, which occur as minerals, correspond to the /AB/AB/AB/... and /ABC/ABC/,... packings respectively.
The cubic form is known to be the low-temperature modification and undergoes a reversible phase transformation2 to the 2H form around 1020![]() C. In addition to these two common modifications, ZnS is known19 to display a large variety of polytype structure with larger identity periods. As stated earlier, all the polytype modifications of a material have identical a and b lattice parameters and differ only along c . The h/a ratio for the 2H modification of ZnS is 0.818 which is somewhat different from the ideal value 0.8165 for a perfect close-packing.
C. In addition to these two common modifications, ZnS is known19 to display a large variety of polytype structure with larger identity periods. As stated earlier, all the polytype modifications of a material have identical a and b lattice parameters and differ only along c . The h/a ratio for the 2H modification of ZnS is 0.818 which is somewhat different from the ideal value 0.8165 for a perfect close-packing.
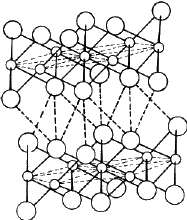
Cadmium iodide
Cadmium iodide is an ionic compound, the ionic radii of Cd and I being 0.97 Å and 2.16 Å respectively2. The structure consists of a close- packing of the I ions with the Cd ions distributed among the octahedral voids. The radius ratio r Cd/r I = 0.45 permits the Cd ions to occupy the octahedral voids. Since there are only half as many Cd ions as I ions in the structure, only half of the total octahedral voids are occupied. Thus the Cd and I layers are not stacked alternately; there is one Cd layer after every two I layers as shown in Fig. 12. The structure therefore consists of molecular sheets (called minimal sandwiches) with a layer of Cd ions sandwiched between two close-packed layers of I ions. The binding within the minimal sandwich is ionic in character and is much stronger than the binding between successive sandwiches which is of van der Waals type. It is because of the weak van der Waals bonding between the successive minimal sandwiches that the material possesses the easy cleavage characteristic of a layer structure. Cadmium iodide structures can have a centre of symmetry in octahedral voids, but cannot have a symmetry plane perpendicular to [00.1]. Cadmium iodide can therefore have five possible space groups - P 3m 1, P ![]() m , R 3m , R
m , R 3m , R ![]() m and P 63mc . Cubic symmetry is not possible in CdI2 on account of the presence of Cd atoms. The most common modifications of CdI2 are 4H and 2H with stacking sequences /A
m and P 63mc . Cubic symmetry is not possible in CdI2 on account of the presence of Cd atoms. The most common modifications of CdI2 are 4H and 2H with stacking sequences /A![]() B C
B C![]() B/...., and /A
B/...., and /A![]() B/A
B/A![]() B/.... respectively, where the Greek letters denote the positions of Cd ions. In addition, this material also displays2,19 a number of polytype modifications of large repeat periods. From the structure of CdI2 it follows that the identity period of all such modifications must consist of an even number of iodine layers. The h/a ratio in all these modifications of CdI2 is 0.805 which differs considerably from the ideal value of 0.8165.
B/.... respectively, where the Greek letters denote the positions of Cd ions. In addition, this material also displays2,19 a number of polytype modifications of large repeat periods. From the structure of CdI2 it follows that the identity period of all such modifications must consist of an even number of iodine layers. The h/a ratio in all these modifications of CdI2 is 0.805 which differs considerably from the ideal value of 0.8165.
 |
Identification of close-packed structures by X-ray diffraction
When a material crystallizes into a number of different close-packed structures all of which have identical layer spacings and different only in the manner of stacking the layers, crystals of the different modifications look alike and cannot be identified by their external morphology. In order to identify such polytype modifications, it is necessary to determine the number of layers in the hexagonal unit cell and the lattice type of the crystal. This can be conveniently achieved by recording reciprocal-lattice rows parallel to c * on single-crystal X-ray diffraction photographs. Since the different polytypes of the same material have identical a and b parameters of the direct lattice, the a * b * reciprocal lattice net is also the same. The reciprocal lattice of these modifications differ only along the c * axis which is perpendicular to the layers. For each reciprocal-lattice row parallel to c * there are others with the same value of the cylindrical coordinate ![]() . For example, the rows 10.l, 01.l,
. For example, the rows 10.l, 01.l, ![]() 1.l,
1.l, ![]() 0.l, 0
0.l, 0![]() .l and 1
.l and 1![]() .l all have
.l all have ![]() =
= ![]() a *
a *![]() . Due to symmetry, it is sufficient to record any one of them on X-ray diffraction photographs. The number of layers, n , in the hexagonal unit cell can be found by determining the c parameter from c -axis rotation or oscillation photographs and dividing this by the known layer-spacing h for that compound (n = c/h ). The density of reciprocal points along rows parallel to c * depends on the periodicity along the c axis. The larger the identity period along c , the more closely spaced are the reciprocal-lattice points along c *. In case of long-period polytypes the number of layers in the hexagonal unit cell can be determined by using a simple alternative method suggested by Krishna and Verma20. This requires the counting of the number of spacings after which the sequence of relative intensities begins to repeat along the 10.l row of spots on an oscillation or Weissenberg photograph. If the structure contains one-dimensional disorder due to a random-distribution of stacking faults, this effectively causes the c lattice parameter to become infinite (c *
. Due to symmetry, it is sufficient to record any one of them on X-ray diffraction photographs. The number of layers, n , in the hexagonal unit cell can be found by determining the c parameter from c -axis rotation or oscillation photographs and dividing this by the known layer-spacing h for that compound (n = c/h ). The density of reciprocal points along rows parallel to c * depends on the periodicity along the c axis. The larger the identity period along c , the more closely spaced are the reciprocal-lattice points along c *. In case of long-period polytypes the number of layers in the hexagonal unit cell can be determined by using a simple alternative method suggested by Krishna and Verma20. This requires the counting of the number of spacings after which the sequence of relative intensities begins to repeat along the 10.l row of spots on an oscillation or Weissenberg photograph. If the structure contains one-dimensional disorder due to a random-distribution of stacking faults, this effectively causes the c lattice parameter to become infinite (c *![]() 0) and results in the production of characteristic streaks along reciprocal lattice rows parallel to c *. It is therefore difficult to distinguish by X-ray diffraction between structures of very large unresolvable periodicities and those with random disorder. Lattice resolution in the electron-microscope has been used in recent years to identify such structures21. Figure 13 depicts the 10.l rows of some close-packed structures of SiC as recorded on c -axis oscillation photographs. When the structure has a hexagonal lattice, the positions of spots are symmetrical about the zero layer line on the c -axis oscillation photograph as seen in Fig. 13 (a) and (b) for the 6H and 36H SiC structures. However, the intensities of the reflections on the two sides of the zero layer line are the same for the 6H structure but not for the 36H . This is because the 6H structure belongs to the hexagonal space group P 63mc whereas the 36H structure belongs to the trigonal space group P 3m 12. The apparent mirror symmetry perpendicular to the c -axis in Fig. 13(a) results from the combination of the 63 screw axis with the centre of symmetry introduced by X-ray diffraction22. For a structure with a rhombohedral lattice, the positions of X-ray diffraction spots are not symmetrical about the zero layer line because the hexagonal unit cell is non-primitive causing the reflections hkl to be absent when
0) and results in the production of characteristic streaks along reciprocal lattice rows parallel to c *. It is therefore difficult to distinguish by X-ray diffraction between structures of very large unresolvable periodicities and those with random disorder. Lattice resolution in the electron-microscope has been used in recent years to identify such structures21. Figure 13 depicts the 10.l rows of some close-packed structures of SiC as recorded on c -axis oscillation photographs. When the structure has a hexagonal lattice, the positions of spots are symmetrical about the zero layer line on the c -axis oscillation photograph as seen in Fig. 13 (a) and (b) for the 6H and 36H SiC structures. However, the intensities of the reflections on the two sides of the zero layer line are the same for the 6H structure but not for the 36H . This is because the 6H structure belongs to the hexagonal space group P 63mc whereas the 36H structure belongs to the trigonal space group P 3m 12. The apparent mirror symmetry perpendicular to the c -axis in Fig. 13(a) results from the combination of the 63 screw axis with the centre of symmetry introduced by X-ray diffraction22. For a structure with a rhombohedral lattice, the positions of X-ray diffraction spots are not symmetrical about the zero layer line because the hexagonal unit cell is non-primitive causing the reflections hkl to be absent when ![]() (
(![]() n = 0, 1, 2,...). For the 10.l row this means that the permitted reflections above the zero layer line are 10.1, 10.4, 10.7 etc. and below the zero-layer line 10.
n = 0, 1, 2,...). For the 10.l row this means that the permitted reflections above the zero layer line are 10.1, 10.4, 10.7 etc. and below the zero-layer line 10.![]() , 10.
, 10.![]() , 10.
, 10.![]() etc. The zero layer line will therefore divide the distance between the nearest spots on either side (namely 10.1 and 10.
etc. The zero layer line will therefore divide the distance between the nearest spots on either side (namely 10.1 and 10.![]() ) approximately in the ratio 1:2. This enables a quick identification of a rhombohedral lattice. Thus the lattice type corresponding to Fig. 13(c) is rhombohedral and the polytype is designated as 90R and belongs to the space group R3m. Figure 13(d) depicts the 10.l row of a disordered 2H SiC structure. The diffuse streak connecting the strong 2H reflections is due to the presence of a random distribution of stacking faults in the 2H structure.
) approximately in the ratio 1:2. This enables a quick identification of a rhombohedral lattice. Thus the lattice type corresponding to Fig. 13(c) is rhombohedral and the polytype is designated as 90R and belongs to the space group R3m. Figure 13(d) depicts the 10.l row of a disordered 2H SiC structure. The diffuse streak connecting the strong 2H reflections is due to the presence of a random distribution of stacking faults in the 2H structure.
 |
Conclusion
Several other materials with close-packed structures are now known to exhibit similar complicated close-packings and it is necessary to point out to students that the hcp and ccp structures are not the only close-packed structures which occur in nature. The mechanism of the formation of long-period polytype structures, with a periodicity much larger than the range of any known atomic forces, has posed a problem in solid-state physics which has yet to be answered satisfactorily. For a detailed account of polytype structures observed in different materials and the different theories put forward to explain their formation, the reader is referred to a book by Verma and Krishna3 and to more recent review articles23,24,25,26.
References
1. Boerdijk, A. H., (1952). Philips, Res. Rept. 7, 303
2. A. R. Verma & P. Krishna, (1966). Polymorphism and Polytypism in Crystals. New York: Wiley. [Russian translation, (1969). Edited by A. S. Povarennykh, MIR: Moscow.]
3. Prager, P. R. (1974) Acta Cryst. A30, 369.
4. Terhell, J. C. J. M. & Van der Vleuten, W. C. (1976). Mater. Res. Bull. 11, 101.
5. Azaroff, L. V. (1960). Introduction to Solids, McGraw-Hill.
6. (1962). International Tables for X-ray crystallography. Vol. III. Birmongham: Kynoch Press.
7. Belov, N. V. (1947). The Structure of Ionic Crystals and Metal Phases (in Russian) Izd. AN SSSR: Moscow.
8. Ramsdell, L. S. (1947). Am. Mineralogist 32, 64.
9. H![]() gg, G. (1943). Ark. Kem. Mineral. Geol. 163, 1.
gg, G. (1943). Ark. Kem. Mineral. Geol. 163, 1.
10. Frank, F. C. (1951). Phil. Mag. 42, 1014.
11. Zhdanov, G. S. (1945). Compt. Rend. Acad. Sci. URSS 48, 43.
12. Pauling, L. (1945). Nature of the Chemical Bond, Cornell Univ. Press: Ithaca.
13. Wyckoff, R. W. G. (1948). Crystal Structures, Vol. I, New York: Interscience.
14. Jagodzinski, H. (1949). Acta Cryst. 2 201.
15. Pandey D. & Krishna, P. (1975). Mater. Sci. Eng. 20, 243; (1976). Mater. Sci. Eng. 26, 53.
16. Jagodzinski, H. (1971) Kristallografiya, 16, 1235.
17. Krishna, P. & Marshall, R. C. (1971) J. Crystal Growth. 9, 319; (1971). J. Crystal Growth . 11 147.
18. Adamsky, R. F. & Merz, K. M. (1959). Z. Krist. 111 350.
19. Trigunayat, G. C. & Chadha, G. K. (1971). Phys. Stat. Sol. A, 4, 1.
20. Krishna P. & Verma, A. R. (1963). Proc. Roy. Soc. (London), Ser A 272, 490.
21. Dubey, M., Singh G. & Van Tendeloo, G. (1977) Acta Cryst. A33, 276.
22. Ramsdell, L. S. & Kohn, J. A.(1951) Acta Cryst. 4, 111.
23. Krishna, P. & Verma, A. R. (1966) Physica Stat. Sol. 17, 437.
24. Shaffer, P. T. B. (1969) Acta Cryst. B25, 477.
25. Trigunayat, G. C. & Verma, A. R. (1976) Crystallography and Crystal Chemistry of Materials with Layered Structures, p. 269. D. Reidel Pub. Co.: Dordrecht-Holland.
26. Krishna, P. & Pandey, D. (1978) Advances in Crystallography Oxford and IBH: New Delhi.