Metric tensor and symmetry operations in crystallography

Germano Rigault

Introduction

In the first part of this monograph the concepts of symmetry operations, symmetry elements and symmetry groups based on the metric tensor invariance are introduced.

In the second part the crystallographic point groups are derived: first the enantiomorphic groups using all possible combinations of the rotation axes; secondly, the centrosymmetric groups; and, finally, the non-enantiomorphic, non-centrosymmetric groups.

This scheme is directed to students who already have a basic knowledge of vector and matrix calculus, and of group theory (i.e. students of the III course in Chemistry).

I hope this presentation will be helpful to teachers in relating some aspects of crystallography to other topics in the field of physical chemistry.

In a crystallography course this subject should be preceded by an introduction to direct lattice and to reciprocal lattice (distances and angles, transformations) and followed by a discussion of space groups, i.e. of the combinations of the possible symmetry operations of the type {A /t }.

Metric tensor

The scalar product of two vectors r₁ and r₂ referred to the same base system consisting of the three non-coplanar vectors $\boldsymbol{\tau}_1$ , $\boldsymbol{\tau}_2$ , $\boldsymbol{\tau}_3$ is defined as:

$\begin{displaymath} \textbf{r}_1 \cdot \textbf{r}_2 = (x_1 \boldsymbol{\tau}_1 +... ...bol{\tau}_1 + y_2\boldsymbol{\tau}_2 + z_2\boldsymbol{\tau}_3).\end{displaymath}$

(1)

In matrix notation it could be written:

$\begin{displaymath} \textbf{r}_1 \cdot \textbf{r}_2 = [x_1y_1z_1]\left[\begin{ar... ...ght] \left[\begin{array} {c} x_2\\ y_2\\ z_2\end{array}\right];\end{displaymath}$

(2)

it is easy to verify that formulae (1) and (2) are equivalent. Relation (2) can be written more briefly as follows:

$\begin{displaymath} \textbf{r}_1 \cdot \textbf{r}_2 = r^t_1Gr_2\end{displaymath}$

(3)

where r₂ is a column matrix

$\begin{displaymath} \left[\begin{array} {c}x_2\\ y_2\\ z_2\end{array}\right]\end{displaymath}$

and r^t₁ a transposed column matrix [ $x_1\,y_1\,z_1$ ]; G is the 3 $\times$ 3 matrix of relation (2) and is called a metric matrix or metric tensor, because its elements $g_{ij} = \boldsymbol{\tau}_i \cdot \boldsymbol{\tau}_j$ are dependent both on the length of the base vectors and on the angles formed by them.

If in (3) we assume r₁ = r₂, we have:

$\begin{displaymath} \textbf{r}_1 \cdot \textbf{r}_1 = \vert\textbf{r}_1\vert \cdot \vert\textbf{r}_1\vert = r^t_1 Gr_1\end{displaymath}$

(4)

and therefore:

$\begin{displaymath} \vert\textbf{r}_1\vert = \sqrt{r^t_1Gr_1}.\end{displaymath}$

(5)

On the other hand, bearing in mind that $\textbf{r}_1 \cdot \textbf{r}_2 = \vert\textbf{r}_1\vert \vert\textbf{r}_2\vert\cos \phi$ , where $\phi$ is the angle between $\textbf{r}_1$ and $\textbf{r}_2$ , we have:

$\begin{displaymath} \textbf{r}_1 \cdot \textbf{r}_2 = \vert\textbf{r}_1\vert\vert\textbf{r}_2\vert \cos \phi = r^t_1Gr_2 \end{displaymath}$

(6)

and finally, using relation (5), we obtain:

$\begin{displaymath} \cos \phi = \frac{r^t_1Gr_2}{\sqrt{r^t_1Gr_1} \cdot \sqrt{r^t_2Gr_2}}.\end{displaymath}$

(7)

Equations (5) and (7) are the rules to obtain the vector lengths and the angles between vectors. The space in which the lengths and the angles between vectors are defined, is called metric space. The metric is given by the G matrix.

Symmetry operations

We can represent every symmetry operation by a matrix A:

$\begin{displaymath} A = \left[\begin{array} {ccc}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32 }&a_{33}\end{array}\right]; (8)\end{displaymath}$

(8)

the value of the elements of this matrix is dependent on the kind and orientation of the corresponding symmetry element with respect to the base system, and on the choice of the latter. In fact, in direct space a symmetry operation transforms a given vector r into the vector r $^{\prime}$ ; in matrix notation we can write:

$\begin{displaymath} r^{\prime} = Ar\end{displaymath}$

(9)

where r and $r^{\prime}$ are the two column matrices whose elements are given by the components of the two vectors.

If the base system is given by the three vectors ${\tau}_1$ , ${\tau}_2$ , ${\tau}_3$ of a primitive lattice, the elements a_ij of the A matrix are necessarily integers. In fact relation (9) must hold true for every vector r of the lattice; A transforms r in another vector r $^{\prime}$ : in this case the components of r and r $^{\prime}$ are integers, and since relation (9) holds for every group of these integers relative to r, the elements of A must be integers.

We will now examine other restrictions on A which allow us to define the single elements a_ij as a function of the metric tensor. A symmetry operation obviously must not change the length of a vector or the angle between vectors. Therefore we have:

$\begin{displaymath} \textbf{r}^{\prime} \cdot \textbf{r}^{\prime} = \textbf{r} \cdot \textbf{r}\end{displaymath}$

from which follows, applying relation (4):

$\begin{displaymath} r^{{\prime}t}Gr^{\prime} = r^tGr\end{displaymath}$

and from (9):

r^tA^tGAr = r^tGr

and finally, since the previous relation must hold for any value of r:

G = A^tGA

(10)

i.e.:

$\begin{displaymath} \left[\begin{array} {ccc} g_{11}&g_{12}&g_{13}\\ g_{12}&g_{2... ...\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{array}\right]\end{displaymath}$

(11)

This identity is the matrix expression of the scalar product conservation on the crystallographic base system. All the matrices satisfying relation (10) are symmetry operations on the base system defined by G (see the example in the Appendix).

From relation (10), using matrix and determinant properties, we obtain:

$\begin{displaymath} \vert G\vert = \vert A^t\vert \cdot \vert G\vert \cdot \vert A\vert\end{displaymath}$

from which, keeping in mind that |A^t| = |A|, follows that the determinant associated with the A matrix must be equal to $\pm$ 1. If the determinant is equal to +1 the symmetry operation is said to belong to the type I and it is defined as a rotation; if the determinant is equal to -1 the symmetry operation is of type II and defined as a rotoinversion.

Symmetry elements and their orientation

The symmetry element is the geometric entity around which one or more symmetry operations take place, and corresponds to the locus of the points that are left unmoved by these operations. The position of the symmetry element is obtained by solving the equation:

Ar = r

from which

(A - 1)r = 0

where 1 is the unit matrix. A solution, other than the trivial solution r = 0, can be obtained only if the condition |A - 1| = 0 is satisfied. If this does not happen, it is necessary to take into account the matrix $A \cdot A$ .

Rotations compatible with a lattice base system

If matrix A represents a type I symmetry operation, we can calculate the rotation angle $\alpha$ from the value of the A matrix trace. We must remember that the trace of A is invariant with respect to a base system transformation.

In a lattice base system the trace is an integer number, since the elements of the matrix are integers. In an orthonormal base system, the counter-clockwise rotation of an angle $\alpha$ , for example, around the z axis is given by:

$\begin{displaymath} \left[\begin{array} {ccc} \cos \alpha& -\sin \alpha& 0\\ \sin \alpha& \cos \alpha& 0\\ 0&0&1\end{array}\right]\end{displaymath}$

and then the trace is equal to $2 \cos \alpha + 1$ .

We have then: $2 \cos \alpha + 1 =$ an integer, from which it is seen that the values of $\alpha$ compatible with a lattice base system are: 60 $^{\circ}$ ,90 $^{\circ}$ , 120 $^{\circ}$ , 180 $^{\circ}$ , 240 $^{\circ}$ , 270 $^{\circ}$ ,300 $^{\circ}$ , 360 $^{\circ}$ .

Symmetry groups

If A₁ and A₂ are two matrices representing a symmetry operation, it is not difficult to demonstrate that the product matrix $A = A_1 \cdot A_2$ also represents a symmetry operation. In fact, since A₁^tGA₁ = G and A₂^tGA₂ = G we have:

$\begin{displaymath} (A_1 \cdot A_2)^t \cdot G \cdot (A_1 \cdot A_2) = A^t_2A^t_1 \cdot G \cdot A_1A_2 = A^t_2GA_2 = G.\end{displaymath}$

This result obviously holds not only for the product of two matrices $A_1 \cdot A_2$ , but also for the product of several matrices $A_1\cdot A_2\cdot A_3 \cdots$ (a special case of this is Aⁿ₁).

Furthermore, if A₁ represents a symmetry operation, A^-1₁ also does: in fact from relation $A^t_1 \cdot G \cdot A_1 = G$ , pre- and post-multiplying both members by (A^t₁)^-1 and by (A₁)^-1 respectively, and keeping in mind that (A^t₁)^-1 = (A₁^-1)^t we obtain:

$\begin{displaymath} G = (A_1^{-1})^t\cdot G\cdot (A_1^{-1}).\end{displaymath}$

Finally it is obvious that matrix 1 represents a symmetry operation (identity) no matter what the base system defined by G may be. In this way we have demonstrated that all group theory postulates are applicable to the symmetry operations. Therefore the symmetry operations are the elements of a group, called a symmetry group. Since all symmetry operations A₁ leave a point with coordinates (0, 0, 0) unchanged, (i.e. all the symmetry elements pass through that point) these symmetry groups are called point groups.

Derivation of the crystallographic point groups

Groups containing only one rotation axis

If A₁ represents a rotation of an angle $\alpha$ around a given axis, A²₁, A³₁, $\ldots$ , Aⁿ₁ = 1 are the symmetry operations corresponding to rotations of $2\alpha$ , $3\alpha$ , $\ldots$ , $n\alpha$ = $360^{\circ}$ respectively, around the same axis; keeping in mind the values of $\alpha$ compatible with a lattice base system we obtain the groups named by the symbol n, i.e. 1, 2, 3, 4, 6.

Groups containing more than one rotation axis

Let us take two symmetry operations: the first one corresponding to a rotation of an angle $\alpha$ around one axis, and the second one to a rotation of an angle $\beta$ around another axis. Let us call $\omega$ the angle between the two axes. Then, the product of the two rotation matrices is also a rotation matrix. The rotation axis of the product matrix is, in general, oriented in a different way than the other two. We can obtain the matrices corresponding to symmetry operations in the following manner: for a given orthonormal vector basis A₁A₂A₃ (Fig. 1), the symmetry operation corresponding to a counter-clockwise rotation of an angle $\alpha$ around the A₃ axis is represented by the matrix:

**Figure 1**
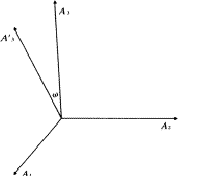
$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

$\begin{displaymath} R_3=\left[\begin{array} {ccc} \cos \alpha&-\sin \alpha& 0\\ \sin \alpha&\cos \alpha&0\\ 0&0&1\end{array}\right]\end{displaymath}$

If, on the other hand, the rotation takes place around the $A^{\prime}_3$ axis, which lies on the plane determined by A₁ and A₃ and forms the angle $\omega$ with A₃ (Fig. 1), the corresponding symmetry operation is given by:

$\begin{displaymath} R_{3^{\prime}} = R_2 \cdot R_3 \cdot R_2^{-1}\end{displaymath}$

where:

$\begin{displaymath} R_2 = \left[\begin{array} {ccc} \cos \omega&0&\sin \omega\\ 0&1&0\\ -\sin \omega&0&\cos \omega\end{array}\right]\end{displaymath}$

represents a counter-clockwise rotation of an angle $\omega$ around A₂. We have to bear in mind, in fact, that $R_2 \cdot R_3 \cdot R_2^{-1}$ represents the symmetry operation R₃ as it is transformed by the operation R₂.

In explicit form we have:

$\begin{displaymath} R_{3^{\prime}} = \left[\begin{array} {ccc} \cos \omega&0&\si... ...in \omega\\ 0&1&0\\ \sin \omega&0&\cos \omega\end{array}\right]\end{displaymath}$

$\begin{displaymath} = \left[\begin{array} {ccc} \cos^2 \omega \cos \alpha + \sin... ...ha&\sin^2 \omega \cos \alpha + \cos^2 \omega\end{array}\right].\end{displaymath}$

The counter-clockwise rotation of an angle $\beta$ around the A₃ axis is given by the matrix:

$\begin{displaymath} R_{3^{\prime\prime}}=\left[\begin{array} {ccc} \cos \beta&-\sin \beta&0\\ \sin \beta&\cos \beta&0\\ 0&0&1\end{array}\right].\end{displaymath}$

The combination of two rotations (one of an angle $\beta$ around the A₃ axis and the other one of an angle $\alpha$ around the $A_{3^{\prime}}$ axis which forms an angle $\omega$ with A₃ and lies on the plane A₁A₃) is also a rotation, represented by the R matrix, given by:

$\begin{displaymath} R = R_{3^{\prime}}R_{3^{\prime\prime}}\end{displaymath}$

$\begin{displaymath} =\left[\begin{array} {ccc} \cos^2 \omega \cos \alpha + \sin^... ...sin^2 \omega \cos \alpha + \cos^2 \omega\end{array}\right]\cdot\end{displaymath}$

$\begin{displaymath} \cdot\left[\begin{array} {ccc} \cos \beta& -\sin \beta& 0\\ \sin \beta& \cos \beta& 0\\ 0&0&1\end{array}\right]\end{displaymath}$

The trace of the R matrix given by the sum of the elements of the principal diagonal, is:

$\begin{displaymath} \left[\begin{array} {ccc} \cos^2 \omega \cos \alpha \cos \be... ...-&-&\sin^2 \omega \cos \alpha + \cos^2 \omega\end{array}\right]\end{displaymath}$

i.e.

$\begin{displaymath} \mbox{trace} = \cos^2 \omega(\cos \alpha \cos \beta + 1) + \... ... -2 \cos \omega(\sin \alpha \sin \beta)+ \cos \alpha \cos \beta\end{displaymath}$

$\begin{displaymath} \phantom{MMMMMN} = \cos^2 \omega(\cos \alpha \cos \beta - \c... ...\sin \beta + \cos \alpha \cos \beta + \cos \alpha + \cos \beta.\end{displaymath}$

(12)

This rotation R must be compatible with the lattice as well. Therefore, the value of the trace, invariant with respect to a base system transformation, must be an integer. The possible values of the trace are: +3, +2, +1, 0, -1. These numbers give the order of the resulting rotation axis.

When we assign to $\alpha$ and $\beta$ in the expression (12) all the possible values, depending upon the order of the rotation axis, we obtain the second degree equations in $\cos \omega$ listed in Table 1, where m is an integer representing the trace of the R matrix.

In Table 1 those solutions for which $\cos \omega$ is greater than 1 are obviously not shown, as well as those that do not give as a result both $\omega$ and 180 $^{\circ}$ - $\omega$ . This last condition is evidently necessary if two axes intersect.

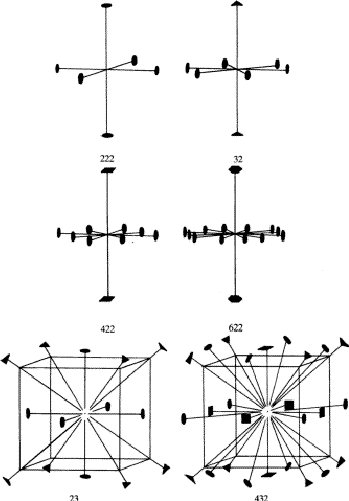
On the basis of the results listed in the table, we can obtain the axis combinations shown in Fig. 2, i.e. the point groups 222, 32, 422, 622, 23, 432.

**Figure 2**
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

Groups containing type II symmetry operations

To derive the point groups which contain type II symmetry operations as well, it is necessary to remember that the product of two operations of the same type is an operation of type I, while the product of two operations of different type is an operation of type II.

In such point groups the operations of type I, equal in number to those of type II, form a group.

Table 1

Order of the axes¹	Trace	m	Possible values of $\omega$	Order of the resultant axis	Orientation²

2-2	$4\cos^2\omega-1-m=0$	+3	0 $^{\circ}$ , 180 $^{\circ}$	1	-
		+2	30 $^{\circ}$ , 150 $^{\circ}$ , 210 $^{\circ}$ , 330 $^{\circ}$	6	010
		+1	45 $^{\circ}$ , 135 $^{\circ}$ , 225 $^{\circ}$ , 315 $^{\circ}$	4	010
		0	60 $^{\circ}$ , 120 $^{\circ}$ , 240 $^{\circ}$ , 300 $^{\circ}$	3	010
		-1	90 $^{\circ}$ , 270 $^{\circ}$	2	010

3-2	$3\cos^2\omega-1-m=0$	+2	0 $^{\circ}$ , 180 $^{\circ}$	6	001
		+1	35 $^{\circ}$ 16', 144 $^{\circ}$ 44', 215 $^{\circ}$ 16', 324 $^{\circ}$ 44'	4
		0	54 $^{\circ}$ 44 $^{\prime}$ , 125 $^{\circ}$ 16 $^{\prime}$ , 234 $^{\circ}$ 44 $^{\prime}$ 305 $^{\circ}$ 16 $^{\prime}$	3
		-1	90 $^{\circ}$ , 270 $^{\circ}$	2	$1/2\,-\sqrt3/2\,0$

4-2	$2\cos^2\omega-1-m=0$	+1	0 $^{\circ}$ , 180 $^{\circ}$	4	001
		0	45 $^{\circ}$ , 135 $^{\circ}$ , 225 $^{\circ}$ , 315 $^{\circ}$	3	$1/\sqrt3\,-1/\sqrt3\,1/\sqrt3$
		-1	90 $^{\circ}$ , 270 $^{\circ}$	2	$1/\sqrt2\,-1/\sqrt2\,0$

6-2	$\cos^2\omega-1-m=0$	0	0 $^{\circ}$ , 180 $^{\circ}$	3	001
6-2	$\cos^2\omega-1-m=0$	-1	90 $^{\circ}$ , 270 $^{\circ}$	2	$\sqrt3/2\,-1/2\,0$

3-3	$9\cos^2\omega-6\cos\omega-3-4m=0$	+3	180 $^{\circ}$	1	-
		0	0 $^{\circ}$ , 109 $^{\circ}$ 28 $^{\prime}$ , 250 $^{\circ}$ 32 $^{\prime}$	3	001
		-1	70 $^{\circ}$ 32 $^{\prime}$ , 289 $^{\circ}$ 28 $^{\prime}$	2

4-3	$3\cos^2\omega-2\sqrt3\cos\omega-1-2m=0$	+1	125 $^{\circ}$ 16 $^{\prime}$ , 234 $^{\circ}$ 44 $^{\prime}$	4
4-3	$3\cos^2\omega-2\sqrt3\cos\omega-1-2m=0$	-1	54 $^{\circ}$ 44 $^{\prime}$ , 305 $^{\circ}$ 16 $^{\prime}$	2

6-3	$3\cos^2\omega-6\cos\omega-1-4m=0$	+2	180 $^{\circ}$	6	001
6-3	$3\cos^2\omega-6\cos\omega-1-4m=0$	-1	0 $^{\circ}$	2	001

4-4	$\cos^2\omega-2\cos\omega-m=0$	+3	180 $^{\circ}$	1	-
		0	90 $^{\circ}$ , 270 $^{\circ}$	3	$1/\sqrt3\,-1/\sqrt3\,1/\sqrt3$
		-1	0 $^{\circ}$	2	001

6-4	$\cos^2\omega-2\sqrt3\cos\omega+1-2m=0$	there are no possible solutions

6-6	$\cos^2\omega-6\cos\omega+5-4m=0$	+3	180 $^{\circ}$	1	-
6-6	$\cos^2\omega-6\cos\omega+5-4m=0$	0	0 $^{\circ}$	3	001

¹The first rotation axis is coincident with A₃, the second one with A_3'.

²The resulting axis orientation is given by the direction cosines referred to the orthonormal base system A₁A₂A₃ and it is obtained solving the equation (R-1)x=0.

From the 11 groups given above we can obtain 11 other point groups which have as elements the type I operations, plus other operations obtained from these by combining them with the inversion operation, represented by the matrix:

$\begin{displaymath} \left[\begin{array} {ccc} \={1}&0&0\\ 0&\={1}&0\\ 0&0&\={1}\end{array}\right].\end{displaymath}$

The centrosymmetric groups so obtained, which have an order double with respect to the order of the groups with which we started, are respectively:

$\begin{displaymath} \={1}, 2/m, \={3}, 4/m, 6/m, mmm, \={3}m, 4/mmm, 6/mmm, m3, m3m.\end{displaymath}$

It is also possible to obtain groups containing type II symmetry operations but which do not contain the inversion operation. In this case we must first obtain, from the starting groups which contain only type I symmetry operations, the corresponding subgroups, which have order $\frac{1}{2}$ with respect to the starting groups.

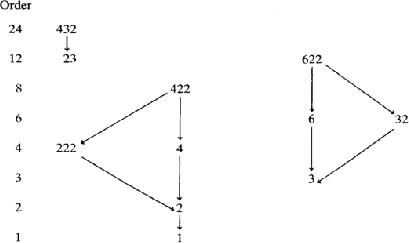
From the scheme shown in Table 2 we see that there are 10 subgroups satisfying this condition. So, to obtain the new groups we multiply by the inversion operation all the operations of the starting group which do not belong to the subgroup.

**Table 2**

$\begin{figure} \includegraphics {table2.ps} \end{figure}$

The sum of the operations obtained in this way, plus the operations belonging to the subgroup, gives all the elements of the new group. The order of the new group is then equal to the order of the starting group.

Let us fully analyse an example: the group 422, of order 8, has the groups 4 and 222 as subgroups of order 4.

In the first case, the subgroup 4 contains the symmetry operations 4¹, 4², 4³, 1; therefore the operations corresponding to a 180 $^{\circ}$ rotation around the axis orthogonal to the 4-fold axis are inverted. In this way we obtain mirror planes parallel to the 4-fold axis, and the resulting point group is 4mm.

In the second case, the subgroup 222 contains three 180 $^{\circ}$ rotations around three perpendicular axes. The operations inverted in this case are $4^1, 4^3, 2_{110}, 2_{1\={1}0}$ . We obtain the operations: $\={4}^1, \={4}^3, m_{(100)}, m_{(1\={1}0)}$ ; the resulting point group is $\={4}2m$ . Altogether we can derive 10 groups, using the following scheme. (The subgroup utilized is shown in parentheses.)

432	$\relbar\kern-2pt\relbar$	(23)	$\longrightarrow$	$\={4}3m$
622	$\relbar\kern-2pt\relbar$	(6)	$\longrightarrow$	6mm
622	$\relbar\kern-2pt\relbar$	(32)	$\longrightarrow$	$\={6}m2$
422	$\relbar\kern-2pt\relbar$	(4)	$\longrightarrow$	4mm
422	$\relbar\kern-2pt\relbar$	(222)	$\longrightarrow$	$\={4}2m$
6	$\relbar\kern-2pt\relbar$	(3)	$\longrightarrow$	$\={6}$
32	$\relbar\kern-2pt\relbar$	(3)	$\longrightarrow$	3m
4	$\relbar\kern-2pt\relbar$	(2)	$\longrightarrow$	$\={4}$
222	$\relbar\kern-2pt\relbar$	(2)	$\longrightarrow$	mm2
2	$\relbar\kern-2pt\relbar$	(1)	$\longrightarrow$	m

Altogether thirty two point groups are possible in three-dimensional space: 11 enantiomorphic; 11 centrosymmetric; and 10 non-enantiomorphic, non-centrosymmetric.

Appendix

Let us examine, as an example, the cubic lattice: since the unit cell constants are $a_0 = b_0 = c_0, \alpha = \beta = \gamma = 90^{\circ}$ , the metric tensor G is given by:

$\begin{displaymath} G = \left[\begin{array} {ccc} g_{11}&0&0\\ 0&g_{11}&0\\ 0&0&g_{11}\end{array}\right].\end{displaymath}$

From relation (10) we have:

$\begin{displaymath} g_{11} \cdot 1 = g_{11} \cdot A^t \cdot 1 \cdot A\end{displaymath}$

and consequently:

$\begin{displaymath} A^t \cdot A = 1.\end{displaymath}$

In this particular case the matrices A are such that their inverse A^-1 is equal to their transposed matrix A^t; therefore we can obtain the following relations:

a₁₁a₁₁ + a₂₁a₂₁ + a₃₁a₃₁ = 1

(11)

a₁₁a₁₂ + a₂₁a₂₂ + a₃₁a₃₂ = 0

(12)

a₁₁a₁₃ + a₂₁a₂₃ + a₃₁a₃₃ = 0

(13)

a₁₂a₁₂ + a₂₂a₂₂ + a₃₂a₃₂ = 1

(22)

a₁₂a₁₃ + a₂₂a₂₃ + a₃₂a₃₃ = 0

(23)

a₁₃a₁₃ + a₂₃a₂₃ + a₃₃a₃₃ = 1

(33)

Relations (11), (22), (33) impose the condition that, in each column of the A matrix, one element is equal to $\pm1$ , and the other two are equal to zero. Relations (12), (13), (23) impose the same condition for each row, since the element different from zero of each column must lie in a different row from the one occupied by the non-zero element of the other two columns.

In conclusion the symmetry operations compatible with a cubic lattice are represented by the following matrices:

$\begin{displaymath} \left[\begin{array} {ccc} 1&0&0\\ 0&1&0\\ 0&0&1\end{array}\r... ...ft[\begin{array} {ccc} 0&1&0\\ 1&0&0\\ 0&0&1\end{array}\right],\end{displaymath}$

$\begin{displaymath} \left[\begin{array} {ccc} 0&1&0\\ 0&0&1\\ 1&0&0\end{array}\r... ...eft[\begin{array} {ccc} 0&0&1\\ 0&1&0\\ 1&0&0\end{array}\right]\end{displaymath}$

plus those obtained from the above matrices, considering, for each of them, all the possible permutations of one, two and three negative signs. It is not difficult to see that from each of the above six matrices, we can obtain seven others containing negative elements. The symmetry operations compatible with a cubic lattice are, thus, 48 in all. Their respective matrices are shown in Table 3. For each matrix in the table the corresponding symmetry operation and the orientation of the symmetry element, derived as above, are given.

From the table it is seen that the symmetry operation corresponding to a rotation of 60 $^{\circ}$ , i.e. symmetry element of order 6, is incompatible with the cubic lattice, but is compatible with a different lattice ( $a_0 = b_0, c_0, \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ}$ ). As it is known, all 32 point groups are subgroups of m3m or 6/mmm or both.

Finally, the relation A^tGA = G can be used to derive, if matrix A is known, the metric tensor compatible with the symmetry operation A.

Table 3. A matrices for the cubic lattice
$\begin{figure} \includegraphics {table3.ps} \end{figure}$

...tensor,: Note that on the basis of the commutative property of the scalar product the G matrix is symmetric.
...rotoinversion.: One can demonstrate in fact that, since the determinant of A is equal to $\pm$ 1, there is no variation of the unit-cell volume; when the value of the determinant is negative the base system passes from a right-handed one to a left-handed one and vice versa.

Crystallography Matters!