The stereographic projection
E. J. W. Whittaker
1. The purpose of the stereographic projection in crystallography
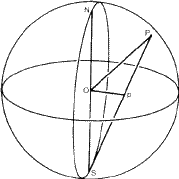
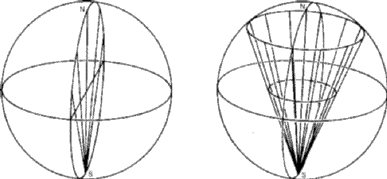
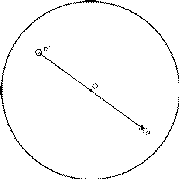
The stereographic projection is a projection of points from the surface of a sphere on to its equatorial plane. The projection is defined as shown in Fig. 1. If any point P on the surface of the sphere is joined to the south pole S and the line PS cuts the equatorial plane at p, then p is the stereographic projection of P. The importance of the stereographic projection in crystallography derives from the fact that a set of points on the surface of the sphere provides a complete representation of a set of directions in three- dimensional space, the directions being the set of lines from the centre of the sphere to the set of points. The stereographic projection of these points is then, for many purposes, the best way of representing on a plane piece of paper the inter-relationship of a set of directions.
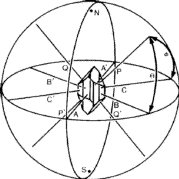
The most common application is that of representing the angles between the faces of a crystal, and the symmetry relations between them. On a `well-formed` crystal all the faces that are related to one another by the symmetry of the crystal structure are developed to an equal extent, and the shape of the crystal therefore reveals its true symmetry. However, real crystals are very rarely well-formed in this way; accidents of crystal growth such as unequal access of the crystallising liquid, or interference by adjacent crystals or other objects, may have impeded the growth of the crystal in certain directions in such a way as to mask the true symmetry. However these accidents do not affect the angles between the faces--only their relative sizes. If the crystal is imagined to lie within a sphere that is centred on some arbitrary point inside the crystal, then normals to the faces can be constructed from this point and extended to cut the sphere (Fig. 2). The points of intersection with the sphere represent the faces of the crystal in terms of direction, entirely uninfluenced by their relative sizes, and the symmetry of the arrangement of these points on the surface of the sphere reveals the true symmetry of the crystal, whether or not it be well-formed. This symmetry can then also be recognised in the stereographic projection of these points.
In this connection the point where the normal to a face cuts the sphere is called the pole of the face. Since the angle between the two faces of a crystal is conventionally defined as the angle between their normals, it is equivalent to the (angular) great circle distance between their poles.
A point on the southern hemisphere projects to a point outside the equator, and as such a point approaches the S-pole its projection recedes to infinity. For many purposes it is convenient to represent the whole sphere within the equator, and this can be done if points in the southern hemisphere are projected to the N-pole instead of the S-pole. It is then usual to distinguish such points by marking those projected to the S-pole as ![]() and those projected to the N-pole as
and those projected to the N-pole as ![]() .
.
A complete stereographic projection of some particular set of points is usually called a stereogram.
2. The properties of the stereographic projection
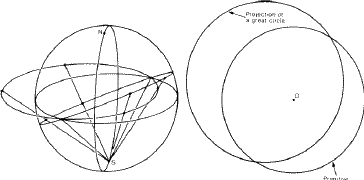
There is, of course, a variety of different projections of the sphere on to a plane that could be used to represent the angular relations between the poles of the faces of a crystal. However, what makes the stereographic projection pre- eminently suitable for this purpose is the fact that it projects any circle on the sphere into a circle on the projection (although in some cases this circle becomes of infinite radius, i.e. a straight line).
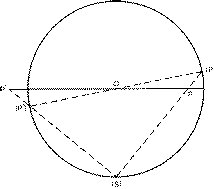
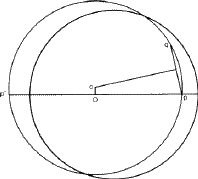
It is evident from Fig. 1 that if P were to lie on the equator of the sphere then p would coincide with it. In other words the equator coincides with its own projection. The circle on the stereographic projection which represents the equator of the sphere plays an important role and is called the primitive of the projection. Angular distances round the equator on the sphere obviously project to identical angular distances round the primitive. It is also clear from Fig. 1 that the north pole of the sphere projects to the centre of the primitive. Figure 3 shows that a meridian of the sphere projects to a diameter of the primitive (this is the case where the projection is a circle of infinite radius), and a circle of latitude on the northern hemisphere projects to a circle concentric with the primitive and inside it. If the circle of latitude were in the southern hemisphere it would project to a concentric circle outside the primitive.
 |
The equator and a meridian are special kinds of great circles on the sphere. A great circle in a general position is shown in Fig. 4, and it is clear that its stereographic projection is a circle of radius greater than that of the primitive. It intersects the latter in two points at opposite ends of a diameter of the primitive. The half of the great circle which is in the northern hemisphere projects to the arc that is within the primitive, and the half in the southern hemisphere projects to the rest of the circle outside the primitive. For some purposes (as discussed in Section 3) it is necessary to consider the whole circle, but for other purposes it is more convenient to project the half-circle in the southern hemisphere to the north pole so as to confine the projection within the primitive. When this is done the complete representation of the great circle consists of two arcs of large radius symmetrically related across a diameter of the primitive as shown in Fig. 5.
 |
The equator and circles of latitude are of course centred at the north pole, and their projections are also centred at the projection of the north pole, that is at the centre of the primitive. However this is the only case in which the projection of the centre of a circle coincides with the centre of the projection of the circle. This is evident for great circles from Fig. 4; that it is also true for small circles will be evident from Section 3(iv) below.
 |
3. Geometrical construction of a stereographic projection
There are four important constructions that can be done very easily on the stereographic projection with the aid of a ruler, compasses and protractor.
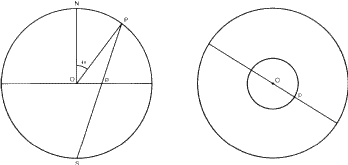
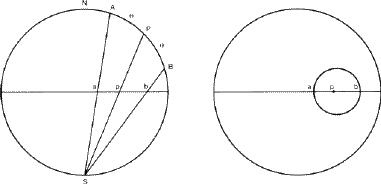
(i) To plot the projection of a point at a given angle ![]() from the N- pole. Consider a meridional section of the sphere through the point P as in Fig. 6a. The point P can be inserted (using the protractor) and joined to S. It cuts the equatorial section at p. A circle of radius Op can then be transferred to the projection (Fig. 6b) and this circle describes the projections of all points at
from the N- pole. Consider a meridional section of the sphere through the point P as in Fig. 6a. The point P can be inserted (using the protractor) and joined to S. It cuts the equatorial section at p. A circle of radius Op can then be transferred to the projection (Fig. 6b) and this circle describes the projections of all points at ![]() from the N-pole. If the orientation of the meridian on which P lies has already been fixed on the stereogram then p is the point where this intersects the circle; if not already fixed by other considerations such a meridian can be drawn in as a diameter of the primitive in an arbitrary orientation.
from the N-pole. If the orientation of the meridian on which P lies has already been fixed on the stereogram then p is the point where this intersects the circle; if not already fixed by other considerations such a meridian can be drawn in as a diameter of the primitive in an arbitrary orientation.
 |
(ii) To plot the projection of the opposite of a given point.
On the meridional section of the sphere through the point P (Fig. 7a) it is easy to join P to the centre and extend it to the opposite point ![]() (its antipodes). The projection of
(its antipodes). The projection of ![]() to the S-pole then gives its projection
to the S-pole then gives its projection ![]() at a distance
at a distance ![]() from the centre. If p has already been plotted on the stereograph (Fig. 7b) then it can be joined to the centre O and this line continued a distance
from the centre. If p has already been plotted on the stereograph (Fig. 7b) then it can be joined to the centre O and this line continued a distance ![]() transferred from Fig. 7a.
transferred from Fig. 7a.
 |
For the following construction (iii) we shall require the opposite of P projected to the S-pole in this way. However, if, for other purposes, we require to project the opposite of P to the N-pole then the procedure is very simple; on this convention ![]() is simply obtained by joining p to the centre of the stereogram and continuing this line for an equal distance beyond the centre to make
is simply obtained by joining p to the centre of the stereogram and continuing this line for an equal distance beyond the centre to make ![]() as in Fig. 8.
as in Fig. 8.
 |
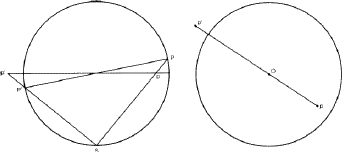
(iii) to draw the projection of a great circle through any two points. Let the projections of the two points P and Q be p and q (Fig. 9). Since every great circle through any point passes through the opposite of that point, the great circle through P and Q must pass through ![]() , the opposite of P. Thus the required projection is the circle through
, the opposite of P. Thus the required projection is the circle through ![]() , and
, and ![]() is found by means of construction (ii). The centre of this circle is at the intersection of the perpendicular bisectors of pq and
is found by means of construction (ii). The centre of this circle is at the intersection of the perpendicular bisectors of pq and ![]() , and the circle can therefore be drawn.
, and the circle can therefore be drawn.
 |
(iv) To draw the projection of a small circle of radius ![]() from a given point. Such a circle is the locus of all points at an angular distance
from a given point. Such a circle is the locus of all points at an angular distance ![]() from the given point P, and is therefore very useful when we wish to plot a point at some specified angle from another point. Consider the meridional section of the sphere through P (Fig. 10a). Mark off two points, A and B at angular distances
from the given point P, and is therefore very useful when we wish to plot a point at some specified angle from another point. Consider the meridional section of the sphere through P (Fig. 10a). Mark off two points, A and B at angular distances ![]() at each side of P. Join A, B and P to S to find their projections a, b and p. Transfer to the stereogram distances ap and bp along the diameter through p. Then a and b obviously lie on the required circle and its centre must be the mid-point of ab. (Note that this centre is displaced outwards from p itself.) The circle can therefore be drawn directly (Fig. 10b).
at each side of P. Join A, B and P to S to find their projections a, b and p. Transfer to the stereogram distances ap and bp along the diameter through p. Then a and b obviously lie on the required circle and its centre must be the mid-point of ab. (Note that this centre is displaced outwards from p itself.) The circle can therefore be drawn directly (Fig. 10b).
 |
It is commonly required to find a point at a given angle from p and at some other given angle from q. Such a point is at the intersection of the two corresponding small circles. There are of course two such points of intersection, but there will usually be some qualitative reason to show which of these two points is the one required.
All the four procedures described above have involved a subsidiary drawing of a meridional section of the sphere; the actual construction has been performed on this section, and appropriate measurements have been transferred from it to the stereogram itself. This use of a subsidiary drawing is helpful in clarifying the principles involved, but it is not necessary in practice. If the meridional section is imagined to be rotated by 90![]() about its equatorial diameter then it coincides with the plane of the stereogram, so that the construction lines can be drawn on the stereogram itself. If they are erased afterwards then the same result is obtained directly without having to transfer a measurement. This way of carrying out construction (ii) is shown by broken lines in Fig. 11, and the method is equally applicable to all the constructions.
about its equatorial diameter then it coincides with the plane of the stereogram, so that the construction lines can be drawn on the stereogram itself. If they are erased afterwards then the same result is obtained directly without having to transfer a measurement. This way of carrying out construction (ii) is shown by broken lines in Fig. 11, and the method is equally applicable to all the constructions.
4. The use of stereographic nets
Stereographic projections of the highest accuracy are obtained by the constructions described in the previous section, and they have been described first because they lead to an understanding of the principles involved. However, it is often more convenient to prepare stereograms with the help of stereographic nets, and although the accuracy obtained is usually lower it is sufficient for most purposes.
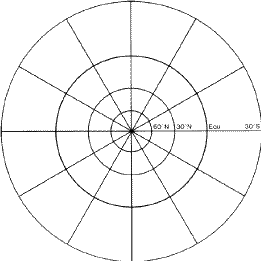
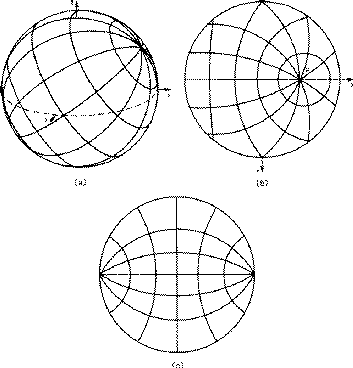
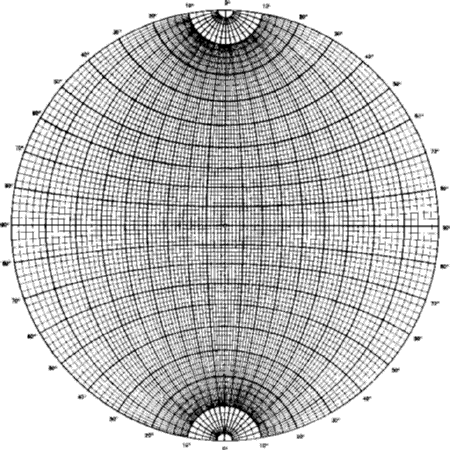
A stereographic net is simply a stereographic projection of the lines of latitude and longitude of a sphere on to a central plane. The most obvious form of stereographic net is shown in Fig. 12. The N-pole projects to the centre as discussed in Section 1, the lines of latitude project to a set of concentric circles, and the lines of longitude to a set of diameters of the primitive. Such a net, if graduated sufficiently finely, could be used directly to obtain the same results as constructions (i) and (iv) of Section 3. However, other nets are possible. If we imagine a terrestrial globe tilted over as shown in Fig. 13a, and we project all points on it, not to the geographical S-pole but to the lowest point of the sphere, then the projection of the lines of latitude and longitude would be as shown in Fig. 13b. We shall revert to this idea in Section 5, but the most generally useful result is if we tilt the globe right over so that its N-S axis is horizontal. The projection is then as shown in Fig. 13c. It is equivalent to what we would have obtained by projecting to its S-pole a globe that was inscribed with lines of latitude and longitude referred to as `east pole` and `west pole`. This is the Wulff net , and is so generally useful that it is commonly referred to as the stereographic net. A commercially available Wulff net of 5 inch diameter graduated in 2![]() intervals is shown in Fig. 14. On this figure all the (nearly) vertical lines represent great circles, and all the (nearly) horizontal lines represent small circles round a point on the primitive.
intervals is shown in Fig. 14. On this figure all the (nearly) vertical lines represent great circles, and all the (nearly) horizontal lines represent small circles round a point on the primitive.
 |
 |
In order to construct stereograms with the help of the Wulff net it is most convenient to work on tracing paper over the net.
To plot a point at a given angle from the N-pole (equivalent to construction (i)) one simply uses the scale along either of the graduated diameters of the net.
To draw a great circle through two points (equivalent to construction (iii)) rotate the stereogram over the net until both points lie on one of the projected great circles (or an interpolated circle between two of them) and then trace the required arc on to the stereogram. Because of the simplicity of this procedure one does not need construction (ii). If the two points have been projected to opposite poles (i.e. one is a ![]() and the other a
and the other a ![]() ) then rotate the stereogram until they lie on projected great circles at equal distances on opposite sides of the vertical diameter of the net.
) then rotate the stereogram until they lie on projected great circles at equal distances on opposite sides of the vertical diameter of the net.
To draw a small circle of given radius ![]() about a point p (equivalent to construction (iv)) rotate the stereogram over the net so that the p point lies on the vertical diameter. If there are two points at the appropriate scale distances on opposite sides of p and within the primitive, then mark these two points and draw a circle through them centred at their mid point (Fig. 15a). If p is closer to the primitive than the required angular radius then only one of the required points (a) can be found on the net. The second point required (b) can most simply be found by using a stereographic ruler. This is a scale whose graduations are equal to those along a diameter of the Wulff net, but which continue appropriately to some (arbitrary) distance beyond the primitive.
about a point p (equivalent to construction (iv)) rotate the stereogram over the net so that the p point lies on the vertical diameter. If there are two points at the appropriate scale distances on opposite sides of p and within the primitive, then mark these two points and draw a circle through them centred at their mid point (Fig. 15a). If p is closer to the primitive than the required angular radius then only one of the required points (a) can be found on the net. The second point required (b) can most simply be found by using a stereographic ruler. This is a scale whose graduations are equal to those along a diameter of the Wulff net, but which continue appropriately to some (arbitrary) distance beyond the primitive.
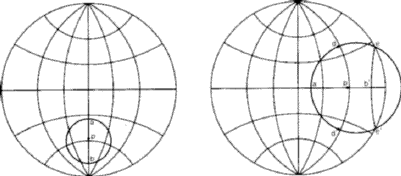 |
However, if a stereographic ruler is not available the Wulff net itself can be used. Position the point p on the horizontal diameter of the net and mark two points d and 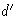 (Fig. 15b) above and below p at distances
(Fig. 15b) above and below p at distances ![]() along the (interpolated) great circle through p. Then the required small circle can be drawn through a, d and
along the (interpolated) great circle through p. Then the required small circle can be drawn through a, d and 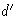 . Once the circle has been drawn it is possible to reproject to the N-pole the part that lies outside the primitive. Count divisions along the diameter from p to the primitive and then continue counting back inwards until the value of
. Once the circle has been drawn it is possible to reproject to the N-pole the part that lies outside the primitive. Count divisions along the diameter from p to the primitive and then continue counting back inwards until the value of ![]() is reached: this leads to a point
is reached: this leads to a point 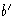 (Fig. 15b) and the required arc is that which goes through
(Fig. 15b) and the required arc is that which goes through 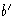 and the two intersections e and
and the two intersections e and ![]() of the small circle with the primitive.
of the small circle with the primitive.
If the point p lies on the primitive, then the stereogram must be rotated so that p lies at one end or the other of the vertical diameter of the Wulff net. A projected small circle of any desired angular radius can then be traced directly from the Wulff net.
5. Representation of symmetry on the stereographic projection
A symmetry plane of a crystal necessarily cuts the spherical projection of the crystal along a great circle. It is therefore represented on the stereogram by a line which will be either the primitive, a diameter of the primitive, or one of the (nearly) vertical arcs of the Wulff net (after rotation into an appropriate orientation). It is represented by a thick line. The operation of reflection of a point p in such a reflection plane to ![]() can be carried out on the Wulff net. Rotate the stereogram so that the line representing the mirror plane coincides with a great circle on the net: then count divisions from p along a small circle until the representation of the mirror is reached. The position of
can be carried out on the Wulff net. Rotate the stereogram so that the line representing the mirror plane coincides with a great circle on the net: then count divisions from p along a small circle until the representation of the mirror is reached. The position of ![]() is then a further equal number of divisions along the small circle beyond the mirror. If the primitive is reached before
is then a further equal number of divisions along the small circle beyond the mirror. If the primitive is reached before ![]() then continue counting divisions inwards until the total is correct, but mark the position
then continue counting divisions inwards until the total is correct, but mark the position ![]() instead of
instead of ![]() .
.
An axis of crystallographic symmetry (2-, 3-, 4- or 6-fold) necessarily intersects the sphere in a point which can be represented by its projection on the stereogram; and marked with the appropriate symbol (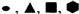 respectively). The same is also true for the direction of the component rotation axis of an axis of rotation-inversion
respectively). The same is also true for the direction of the component rotation axis of an axis of rotation-inversion ![]() ,
, ![]() or
or ![]() (marked as
(marked as 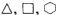 respectively). The operation of an n-fold symmetry axis on a point p is to rotate p through graduations equivalent to 360
respectively). The operation of an n-fold symmetry axis on a point p is to rotate p through graduations equivalent to 360![]() /n along a small circle round the pole of the axis. If the latter is at the centre of the stereogram then this is a straight-forward rotation of 360
/n along a small circle round the pole of the axis. If the latter is at the centre of the stereogram then this is a straight-forward rotation of 360![]() /n. If the pole of the symmetry axis lies on the primitive, then place the stereogram so that this point lies at the bottom of the Wulff net. Increments of 360
/n. If the pole of the symmetry axis lies on the primitive, then place the stereogram so that this point lies at the bottom of the Wulff net. Increments of 360![]() /n may then be counted in terms of the graduations along the small circle through p. When the primitive is reached counting continues as the path is retraced but the next point is plotted as
/n may then be counted in terms of the graduations along the small circle through p. When the primitive is reached counting continues as the path is retraced but the next point is plotted as ![]() instead of
instead of ![]() (or vice-versa).
(or vice-versa).
If the symmetry axis is in a more general position it would seem that one would require a stereographic net of the kind shown in Fig. 13 with the intersection of the meridians at the position of the symmetry axis. However, it is perfectly possible to use the Wulff net in the following way, repositioning the stereogram on the net as necessary.
(i) Measure the angular distance from the axis of symmetry (s) of the point (p) that is to be repeated by the symmetry.
(ii) Construct the small circle (l) of this radius about s.
(iii) Construct the circle (e) of radius 90![]() about s. To construct this place s on a diameter of the net, find the point 90
about s. To construct this place s on a diameter of the net, find the point 90![]() away along that diameter and the two ends of the perpendicular diameter, and draw a circle through these three points. Although constructed as a small circle, this is in fact a great circle, so that angular distances can be measured along it.
away along that diameter and the two ends of the perpendicular diameter, and draw a circle through these three points. Although constructed as a small circle, this is in fact a great circle, so that angular distances can be measured along it.
(iv) Mark the intersection of e with the great circle through s and p. Count increments of 360![]() /n from this point along e. From each of these incremental points find the great circle that goes through s; the points in which these great circles cut l are the points in which p is repeated by the axis of symmetry.
/n from this point along e. From each of these incremental points find the great circle that goes through s; the points in which these great circles cut l are the points in which p is repeated by the axis of symmetry.
If the poles of the faces of a crystal of unknown symmetry are plotted in an arbitrary orientation on a stereogram it will often be possible to recognise the orientation of the symmetry elements. The stereogram can then be re-plotted in one of the standard orientations, shown in text-books of morphological crystallography to demonstrate the symmetry of the seven crystal systems and the thirty two crystal classes.
6. Calculations based on the stereogram
Any three intersecting arcs of great circles on the sphere constitute a spherical triangle. Such a triangle has six elements: the three sides which are specified by the angles which they subtend at the centre of the sphere; and the three angles which are defined as the dihedral angles between the central planes that intersect the sphere in the great circles. If any three elements of a spherical triangle are known the remainder can be calculated by the methods of spherical trigonometry. A full discussion of these methods is beyond the scope of this booklet, but if the triangle has vertices A, B, C and the sides opposite to these vertices are denoted a, b, c respectively, the two most generally useful formulae are:
![]() =
= ![]() =
= ![]()
and
![]() .
.
The latter may be rewritten with appropriate inter-changes of the elements concerned.
By joining up the poles on a stereogram by projections of great circles it is always possible to find spherical triangles from which one can calculate by spherical trigonometry previously unmeasured angles between poles. It frequently happens that the directions of crystallographic axes are not marked by the poles of faces on a crystal, but they can nevertheless be found as the intersection of appropriate circles on the stereogram. Suitable spherical triangles can then be found to permit the calculation of inter-axial angles and axial ratios from the angles between available faces. A full treatment of these methods is given in books on morphological crystallography.
7. Other uses of the stereographic projection in crystallography
Any problem involving only directions in space can be reduced to a problem relating to a distribution of points on a sphere, and can therefore be represented in a stereogram. The symmetry relationships between the components of a twin (or of a more complex intergrowth of more than two individual crystals) can obviously be represented in this way. For partially orientated polycrystalline aggregates (e.g. rolled metal sheets, stretched polymers, rock textures) the orientations in space of the normal to some particular crystallographic plane can be plotted on the stereogram, and contours can be drawn to indicate the range of orientations involved. Such diagrams are known as pole figures.
Acknowledgements
Figures 1, 2, 3, 7a, 9, 10, 12, 13a and 13b are reproduced by permission of Pergamon Press from Crystallography: An Introduction for Earth Science (and other Solid State) Students by E. J. W. Whittaker.
Figure 14 is reproduced by permission of The Institute of Physics, 47 Belgrave Square, London, from whom copies may be purchased.
Permission to reproduce these illustrations is gratefully acknowledged.
Further reading
Applications of the stereographic projection are dealt with in the following books.
Representation of crystallographic symmetry. Whittaker, E. J. W., Crystallography: An Introduction for Earth Science (and other Solid State) Students , Pergamon Press (1981).
Pole figures and preferred orientations. Henry, N. F. M., Lipson, H. and Wooster, W. A., The Interpretation of X- Ray Diffraction Photographs , Macmillan (1961)
Peiser, H. S., Rooksby, H. P. and Wilson, A. J. C., X-Ray Diffraction by Polycrystalline Materials , London, The Institute of Physics (1955).