An article commenting on this pamphlet has been published in Journal of Applied Crystallography: L. Suescun and M. Nespolo (2012). From patterns to space groups and the eigensymmetry of crystallographic orbits: a reinterpretation of some symmetry diagrams in IUCr Teaching Pamphlet No. 14. J. Appl. Cryst. 45, 834-837 [ doi:10.1107/S002188981201998X]

Space group patterns

M. W. Meier

Introduction

Two-dimensional periodic patterns provide a simple means for teaching the principles of crystallographic symmetry. In particular they help to develop some desirable skill in recognizing space groups at an elementary level. Crystal structure models are generally less useful for demonstrating space group symmetry. This account shows how 2-dimensional patterns can be extended to include 3-dimensional space group symmetry. Space group patterns, as presented in this brief exposition, can furnish a suitable basis for a non-mathematical introduction to the symmetry of crystal structures in which the emphasis is on practical rather than theoretical aspects.

A knowledge of elementary symmetry concepts, as outlined in Pamphlet No. 13 of this series or an introductory text, is assumed.

Two-dimensional periodic patterns

Plane groups can be illustrated using a great variety of 2-dimensional periodic patterns. Unexcelled classics are the widely known prints by M. C. Escher¹ which have found their way into many texts on crystallographic symmetry. Other examples are provided by decoration and gift wrapping paper, various fabrics and highly artistic designs including Arabic geometrical patterns.²

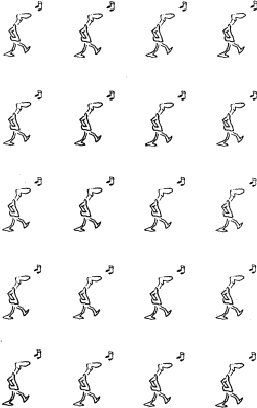
A standard introductory exercise in crystallographic symmetry is the determination of the plane group of such patterns, e.g. that of an ordinary brick wall (c2mm). The best approach to such a problem is to begin with the point symmetry (extended by glide lines if necessary) which will define the system of axes to be adopted. Thus, the oblique system (comprising plane groups p1 and p2) is by no means characterized by $a \neq b$ and $\gamma \neq 90^{\circ}$ , a frequent misconception in 'defining' crystal systems. A sheet of stamps, for example, has symmetry p1 in general,³ and therefore belongs to the oblique system. The rectangular form of the stamps is not required by symmetry, it simply happens to be convenient. Another example of this sort is presented in Fig. 1.

**Figure 1:** Example of two-dimensional periodic pattern having symmetry p1 (note oblique system despite 'rectangular' unit cell).
$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

Some knowledge of and practice in recognizing plane groups is not necessarily a prerequisite but a good basis from which to start an introduction to space group symmetry as described in the following sections. The pattern in Plate (i), if considered to represent a 2-dimensional structure, serves as an example for a preliminary exercise on plane groups. (Enter the symmetry elements and unit cell, and determine the plane group of the pattern.)

Space group operations

Space groups comprise two types of symmetry operations:

(a) purely translational operations expressed by the Bravais lattice (denoted by a capital letter in the space group symbol), and

(b) operations of point symmetry elements, glide planes and/or screw axes, as listed in the following table:


Symmetry element	Point symmetry elements	Symmetry elements involving translations

of the first kind	rotation axes	screw axes
(proper)	1 2 3 4 6	2₁ 3₁ 3₂ 4₁ 4₂ 4₃ etc

of the second kind	rotary inversion	glide planes
(improper)	axes	a b c n d
	$\overline{1}$ $\overline{2}$ $\overline{3}$ $\overline{4}$ $\overline{6}$

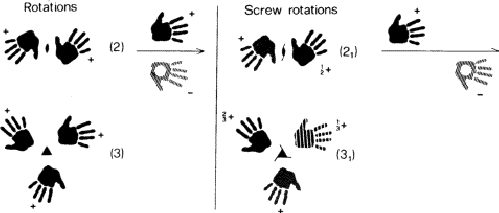
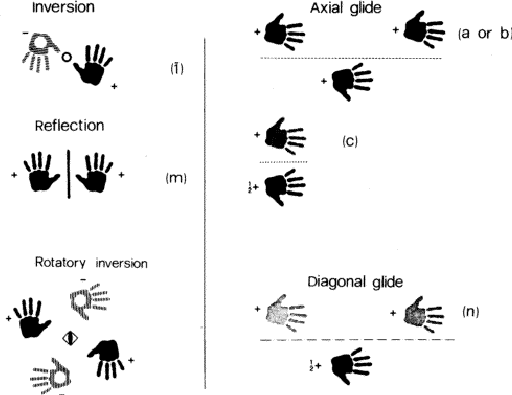
These symmetry operations can be depicted as shown in Figs. 2 and 3 (if necessary, see also Fig. 4 for explanation of the diagrams). Symmetry operations of the second kind, unlike those of the first kind (or proper operations), transform a right-handed into a left-handed object and vice versa. Two enantiomeric objects can be related only by a symmetry operation of the second kind (or an improper operation). This distinction of the two kinds of symmetry elements is also of considerable practical importance, as it will soon be evident, in recognizing the space group of a given pattern.

**Figure 2:** Symmetry operations of the first kind (examples).
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

**Figure 3:** Symmetry operations of the second kind.
$\begin{figure} \includegraphics {fig3.ps} \end{figure}$

**Figure 4:** Scheme used in space group patterns (worksheets (i) to (xv)).
$\begin{figure} \includegraphics {fig4.ps} \end{figure}$

Some point symmetry operations (which leave at least one point in space unaffected) are shown on the left hand side of Figs. 2 and 3. Examples of operations containing translational components (which are incompatible with a finite array of objects) are presented on the right hand side in these figures.

More details on crystallographic symmetry elements can be readily obtained from most textbooks on crystallography.⁴ For information on symbols and notation it is best to consult the International Tables.⁵

Introductory examples of space group patterns and their use

Hands or feet are particularly suitable elements for constructing periodic patterns for teaching space group symmetry at an elementary level. Elements of this sort, when arranged to form periodic patterns, are comparable to molecular building units of crystal structures. The principal advantage of the former is that their 'handedness' can be spotted at a glance and in this way symmetry elements of the first and of the second kind (e.g. such as 4₂ and $\overline{4}$ ) can be readily distinguished.

A simple example of a pattern representing the space group Pma 2 is shown in Plate (i). The mirrors, a -glide planes and the 2-fold rotation axes perpendicular to the plane of the figure can be easily located.

Unless noted otherwise, conventional orientation of the coordinate axes will be assumed in all discussions of space group patterns throughout this text. The plane of the diagram is thereby supposed to be parallel to x (down the page) and y (across the page), with the z-axis coming out of the plane (towards the viewer since the coordinate system should be right-handed).

The space group of the pattern is determined by first entering the symmetry elements into the figure using conventional crystallographic designations. The use of tracing paper (placed on the patterns) is recommended for drawing up these diagrams of symmetry elements. This not only assures that the patterns can be re-used, but also allows occasional mistakes to be rectified without leaving disturbing marks in the pattern.

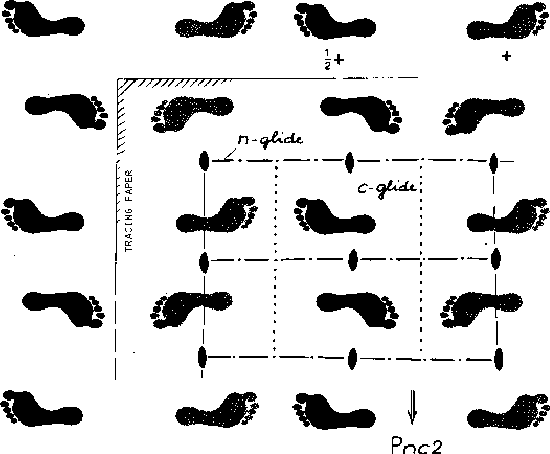
An example of a completed tracing showing the diagram of symmetry elements is supplied in Fig. 5 for the patterns of Plate (ii). It is advisable to enter the symmetry elements systematically beginning with those which are needed to define the crystal system and which help in the selection of a suitable origin for the crystallographic axes. (The latter may well be tentative at this stage.) The unit cell can then be outlined so that boundaries, within which all further symmetry elements are to be located, will be set. Let us now return to the pattern on Plate (ii). Point symmetry elements are found by considering pairs of black feet (at $\frac{1}{2}$ + z). Since these are all left feet the symmetry elements are of the first kind: 2-fold rotation axes in between neighboring black feet. Similarly, 2-fold rotation axes are also noted to occur in between the right feet marked in grey (at +z). Pairs of black (left) and grey (right) feet which can only be related by a symmetry element of the second kind are considered next. The c-glide plane is relatively easy to recognize. Monoclinic symmetry can be ruled out at this stage since the c-glide plane is parallel and not perpendicular to the 2-fold rotation axis. Since orthorhombic symmetry is therefore expected, the pattern is searched next for additional glide planes (since mirror planes are clearly absent) at right angles to the c-glide planes. Thus, n-glide planes, relating left and right feet, running through the 2-fold rotation axes are detected, and orthorhombic symmetry is thereby confirmed. The origin is conveniently placed in a position of maximum point symmetry, i.e. a 2-fold rotation axis. The unit cell can now be outlined and careful inspection reveals no other types of symmetry elements. The lattice is noted to be primitive and, remembering that in the orthorhombic system the symmetry elements refer to directions [100], [010], [001], in this order, the space group of the pattern must consequently be Pnc2. A simple list of space groups may now be consulted for checking purposes and Pnc2 is found to be listed as space group No. 30.

**Figure 5:** Completed worksheet.
$\begin{figure} \includegraphics {fig5.ps} \end{figure}$

The space group of the pattern in Plate (iii) can be arrived at in similar fashion. It is found to be Pbn2₁. One may wonder, however, why Pbn2₁ is not included in an ordinary list of space groups. The reason for this is not difficult to find. Pbn2₁ and Pna2₁ (listed as No. 33) denote the same space group but refer to different settings. This can be seen fairly easily using pattern (iii). If the pattern is rotated by 90 $^{\circ}$ around z (i.e. 2₁) the feet will be oriented parallel to the x-axis and the space group symbol of the pattern will change to Pna2₁. Because of conventions, which we need not consider here in detail, Pna2₁ is normally listed in tables of space groups (in so-called standard setting) but Pbn2₁ is equally acceptable. Frequently one has a good reason to use a space group in an alternate setting. (We shall find such a reason shortly when comparing patterns (iii) and (vi).)

Patterns (iv) and (v) can be considered jointly. A certain resemblance is apparent. All objects in (iv) are also present in (v) and the symmetry of the latter is distinctly higher. Detailed examination along the lines described will lead to space group Cmc2₁ for pattern (v) and Cc for (iv). As indicated by the space group symbols the latter is a subgroup of the former.⁷

A subgroup relation which is less obvious can be found when patterns (vi) and (iii) are compared. The space group Aba2 of pattern (vi) does not by itself suggest that Pbn2₁ is a subgroup thereof. However, the pattern does, particularly after the symmetry elements have all been entered. As an instructive exercise all those feet in pattern (vi) which have to be suppressed in order to reduce the symmetry of the pattern of Pbn2₁ can be crossed out.

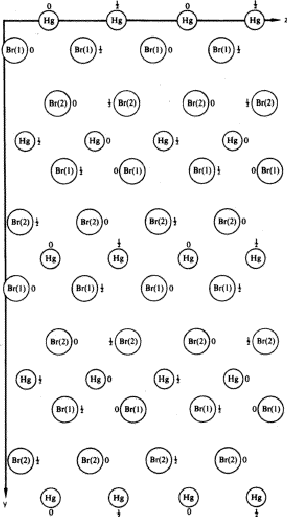
It seems appropriate to conclude this first series of examples by a comparison of the patterns with crystal structures. The relatively simple crystal structure of HgBr₂ shown in Fig. 6 is taken from a textbook. It is a typical example demonstrating that, with respect to space group symmetry, customary diagrams of crystal structures are considerably more troublesome than comparable patterns of the type presented in this text. Despite the fact that the origin is marked in the structure of Fig. 6 (which certainly helps) the practical problem of recognizing the space group symmetry requires much more effort. As a hint it may be pointed out that the space group of this stucture is the same as that of one of the feet patterns shown in Plates (i) to (vi), making possible a direct comparison.

**Figure 6:** Crystal structure of HgBr₂ in projection onto (100) (adapted from Reference 6).
$\begin{figure} \includegraphics {fig6.ps} \end{figure}$

Plate (i) to (vi). Worksheets for practical exercises.

Select thumbnail for large (1280x888 pixels, typically 20kB) image.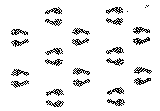

Plate i	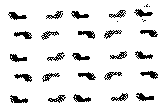Plate ii	Plate iii
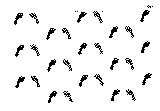Plate iv	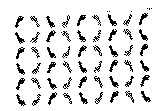Plate v	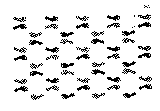Plate vi

Further examples including more complicated space groups

Once a bit of experience has been acquired in using these patterns to learn about space groups it is tempting to consider some more complicated cases. The examples in Plates (vii) to (xv) provide more opportunities to 'discover' some of the idiosyncrasies of space groups. To get the full benefit of such studies, aids, if at all necessary, should be limited to a simple list of the 230 space groups in standard notation. (The International Tables,⁵ however useful they are in general, should not be used in this connection except perhaps for the occasional checking of results.)

In the patterns based on feet the tacit assumption is made that they are all looking the same way up. When using hands for patterns it is somewhat simpler to indicate which side of the object is looking upwards. As has already been shown in Fig. 2 to 4 a coin (white dot) in a hand is used as a simple indication that the palm of the hand is oriented upwards (otherwise it is oriented downwards). Thus, patterns (vii) and (ix) could also be composed of feet (as before) but not the other designs based on hands.

The space groups of the remaining patterns, from (vii) onwards, are not directly disclosed in the text portion of this account in consideration of readers who prefer to find out themselves. (See References and Notes for solutions.) Patterns (x) to (xv) can also serve for more advanced exercises. Particularly in case of such patterns of higher symmetry it is not so simple to draw up complete diagrams of symmetry elements (i.e. without missing any of the symmetry). When this appears possible the following procedure should be incorporated in the exercise. After having decided upon a unit cell and space group it is a simple matter to determine p, the number of equipoints for a general position, since this equals the number of hands per unit cell. Hands marking equivalent (but not identical) positions are then numbered from 1 to p. The main part of the exercise is then to determine the space group operations for $1 \rightarrow 2$ , $1 \rightarrow 3$ $\dots$ $1 \rightarrow p$ . In this way, symmetry elements which may have been overlooked before are likely to emerge.

Other questions which arise naturally in exercises based on space group patterns pertain to

the point symmetry of special positions,
the choice of the origin (cf. patterns (x) and (xii)),
alternate settings of the space group, etc.

Pattern (viii) provides another example of a space group in a non-standard setting. Two of the patterns have been included to show that space groups like $P\overline{4}2c$ and $P\overline{4}c2$ or $P\overline{4}2m$ and $P\overline{4}m2$ do not differ merely with respect to the setting as one might be inclined to think on the basis of the corresponding crystal class $\overline{4}2m$ , but are truly different space groups.

Plate (vii) to (xv). Worksheets for practical exercises.

Select thumbnail for large (1280x888 pixels, typically 20kB) image.

Plate vii	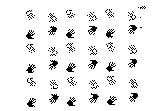Plate viii	Plate ix
Plate x	Plate xi	Plate xii
Plate xiii	Plate xiv	Plate xv

Concluding remarks

Over a hundred space groups can be easily treated using such patterns, and expanding the series to encompass more space groups would pose no problems. In particular, some space groups frequently observed in molecular packings (such as $P\overline{1}$ , P2₁, P2₁2₁2 and Pca2₁) can be represented in this manner.⁸

This brief description includes patterns of more space groups than one would normally cover in a non-mathematical introductory course and is meant to provide some choice. For non-crystallographers, who make up the vast majority of students in crystallography classes, some half a dozen suitably chosen patterns, if extensively dealt with, should normally be adequate to develop some desirable skill in recognising a space group and to convey a sufficient understanding of the subject for practical purposes.

Acknowledgements

I am indebted to many of my colleagues for useful comments, especially to Dr. Ch. Baerlocher, Dr. L. Dent Glasser, Dr. L. B. McCusker and Dr. J. H. Robertson.

References and notes

1. An annotated collection of these prints can be found in Macgillavry, C. H., Symmetry Aspects of M. C. Escher's Periodic Drawings, International Union of Crystallography (1965).

2. The use of Arabic geometrical patterns in crystallographic teaching has been discussed by E. and M. Makovicky in N. Jb. Miner. Mh., 1977, 58-68. Numerous illustrations can be found in a book by J. Bourgoin (Arabic Pattern and Design, originally published in 1879 (in French) and reprinted without text by Dover in 1973).

3. The back side of a stamp sheet displays a higher symmetry for it shows the lattice only and not the structure.

4. cf. Bloss, F. D., Crystallography and Crystal Chemistry, Holt, Rinehart and Winston (1971); Buerger, M. J., Elementary Crystallography, Wiley (1963); Dent Glasser, L. S., Crystallography and its Applications, Van Nostrand Reinhold (1977); Megaw, H. D., Crystal Structures: A Working Approach, Saunders (1973).

5. International Tables for X-ray Crystallography Vol. I (1952).

6. Sands, D. E., Introduction to Crystallography. Benjamin (1969).

7. The two patterns (iv) and (v) can indeed serve to illustrate various aspects of a subgroup relation.

8. A set of worksheets comprising additional space groups can be obtained from the author (Prof. W. M. Meier, Institute of Crystallography and Petrography, ETH, 8092 Zurich, Switzerland).

Plate (i) to (xv). Worksheets for practical exercises.

Select thumbnail for large (1280x888 pixels, typically 20kB) image.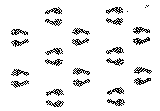

Plate i	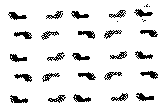Plate ii	Plate iii	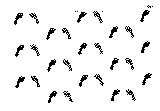Plate iv
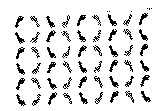Plate v	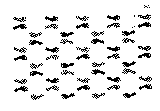Plate vi	Plate vii	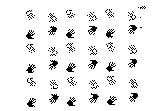Plate viii
Plate ix	Plate x	Plate xi	Plate xii
Plate xiii	Plate xiv	Plate xv

List of space groups represented in plates (i) to (xv)

(i) Pma2 (plane group pmg)

(ii) Pnc2

(ii) Pbn2₁

(iv) Cc

(v) Cmc2₁

(vi) Aba2

(vii) Pnn2

(viii) P2₁22

(ix) P31c

(x) Pban

(xi) $P\overline{4}2_1m$

(xii) P4/nbm

(xiii) $P\overline{4}b2$

(xiv) $P\overline{4}2m$

(xv) $P\overline{4}m2$

Space group of structure in Fig. 4: Pbn2₁.

Crystallography Matters!

Space group patterns

M. W. Meier

Introduction

Two-dimensional periodic patterns

Space group operations

Introductory examples of space group patterns and their use

Plate (i) to (vi). Worksheets for practical exercises.

Further examples including more complicated space groups

Plate (vii) to (xv). Worksheets for practical exercises.

Concluding remarks

Acknowledgements

References and notes

Plate (i) to (xv). Worksheets for practical exercises.

List of space groups represented in plates (i) to (xv)