An introduction to crystal physics

Description of the physical properties of crystals

Ervin Hartmann

Introduction

Most monographs on physics discussing the physical properties of matter usually proceed from isotropic materials and as a generalization include a more or less limited description of the behaviour of crystalline bodies. This way of presentation is doubtless advantageous, however, it implies a separate discussion of the various properties, inevitably obscuring the general principles and methods applicable in the theory of crystal properties. The purpose of the present work is to discuss and summarize in a unified treatment the physical properties of crystals, and to illustrate by some typical examples the principles and methods underlying a uniform description of these properties.

For an introduction, in order to develop a clear crystal physical picture, let us investigate the problem of the dielectric susceptibility in an isotropic and an anisotropic medium respectively.

**Figure 1:** Formation of dipoles (a) in isotropic, (b) in anisotropic insulators.
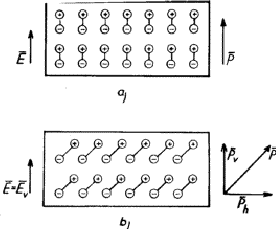
$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

In isotropic insulators the dipoles generated in the course of dielectric polarization are parallel with the electric field (Fig. 1a), consequently the relation between the vector of the electric polarization ( $\=P$ ) and the electric field ( $\=E$ ), that is the susceptibility, can be characterized by one single value ( $\chi$ ).

$\begin{displaymath} \=P=\chi\=E.\end{displaymath}$

(1.1)

In an anisotropic medium, however, the dipoles formed during the dielectric polarization are generally not parallel with the electric field. Fig. 1b depicts the relatively simple case in which the dipoles though arranged in a plane parallel with the electric field (represented by the plane of the drawing) have a different direction. In this case the vector of the electric polarization ( $\=P$ ) due to the vertical electric field ( $\=E$ = $\=E_v$ )) has not only a vertical ( $\=P_v$ ) but also a horizontal component ( $\=P_h$ ). Consequently in the case of Fig. 1b two quantities ( $\chi_{vv}$ ; $\chi_{hv}$ )are necessary to describe the relation between the vertical electric field and the electric polarization, and the components of the two vectors in question are connected by the equations

$\begin{displaymath} \=P_v = \chi_{vv}\=E_v\end{displaymath}$	(1.2)
$\begin{displaymath} \=P_h = \chi_{hv}\=E_v.\end{displaymath}$

Generally, when investigating the dielectric polarization in the three dimensional space one finds that, disregarding the higher order effects, in an x₁, x₂, x₃ coordinate system the following equations hold between the components of the vector of the electric field ( $\=E$ = [E₁, E₂, E₃]) and the components of the electric polarization ( $\=P$ = [P₁, P₂, P₃]):

$\begin{displaymath} P_1 = \chi_{11}E_1 + \chi_{12}E_2 + \chi_{13}E_3\end{displaymath}$

$\begin{displaymath} P_2 = \chi_{21}E_1 + \chi_{22}E_2 + \chi_{23}E_3\end{displaymath}$

(1.3)

$\begin{displaymath} P_3 = \chi_{31}E_1 + \chi_{32}E_2 + \chi_{33}E_3.\end{displaymath}$

This means that altogether nine data are necessary to describe the relation between the electric field and the electric polarization. By means of vector algebra it can be shown that in case of an orthogonal coordinate transformation the nine coefficients in the eq. (1.3) transform as the products of the components of two vectors, i.e. they are components of a second-rank tensor. Consequently the dielectric susceptibility in an anisotropic medium can be described by a second-rank tensor.

Equations (1.3) can be rewritten in an abbreviated form

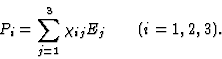$\begin{displaymath} P_i = \sum^3_{j=1} {\chi}_{ij}E_j \qquad (i = 1, 2, 3).\end{displaymath}$

(1.4)

With Einstein's notation the $\sum$ symbol can be omitted if in the same term a suffix occurs twice. Accordingly eq. (1.4) takes the following form

$\begin{displaymath} P_i = \chi_{ij}E_j \qquad (i, j = 1, 2, 3).\end{displaymath}$

(1.5)

In the forthcoming discussions the Einstein convention will be used.

2. Physical properties as tensors

It has been demonstrated in the introduction that the dielectric susceptibility of an anisotropic medium can be described with a second-rank tensor which expresses the relation between two physical quantities i.e. the relation between the vector of polarization and the vector of the electric field. Similarly the greater part of the various physical properties may be described with a tensor which establishes the relation existing between measurable physical tensor quantities. Every scalar is a zero-rank, and every vector a first-rank tensor. Generally in crystal physics a set of 3^r quantities with r indices transforming under transition from the old coordinates to the new ones as the products of the components of r vectors is called a polar (or true) tensor of rank r.

Accordingly if the [B_ijk...n] and [A_pqr...u] tensors represent physical quantities the general form of the relation between these quantities may be written (in first-order approximation) using the Einstein's convention as follows

$\begin{displaymath} B_{ijk...n} = a_{ijk...npqr...u} \cdot A_{pqr...u} \qquad (i, j, k,\dots n, p, q, r,\dots u = 1, 2, 3)\end{displaymath}$

(2.1)

where the tensor [a_{ijk...npqr...u}] denotes the physical property connecting the two physical quantities.

It follows from the tensor algebra that if [A_pqr...u] denotes an f-rank and [B_ijk...n] a g-rank tensor the [a_{ijk...npqr...u}], denoting the physical property, must be an (f + g)-rank tensor.

Let us consider some examples. In a given state the density of matter expresses the relationship between its mass and volume, they are represented by 0-rank tensors, consequently the density is represented by a 0-rank tensor (i.e. a scalar). The pyroelectric properties of crystals are described by a first-rank tensor. The pyroelectric tensor, (essentially a vector) represents the relation between a first-rank tensor (the vector of electric polarization) and a zero-rank tensor (the temperature). Besides the dielectric susceptibility, the electrical conductivity, the heat conductivity, the thermal expansion and so on may be represented by a second-rank tensor. Further examples including properties which can be expressed with higher-rank tensors are summarized in Table 1.

Crystals have further on also some anisotropic properties which cannot be directly represented by tensors, such properties - not to be discussed in this paper - are for instance the tensile strength, flow stress, surface energy, rate of growth and dissolution, and so on.

**Table 1:** Tensors representing physical properties
Property or effect	Tensor notation	Tensor rank	Maximum no. of independent components	Defining equation	Physical quantities in the defining equation
Density	$\rho$		1	$\Delta m = \rho\Delta V$	$\Delta m$ mass	$\Delta V$ volume
Specific heat	c		1	$\Delta S=\displaystyle \frac{c}{T}\Delta T$	$\Delta S$ entropy	T temperature
Pyroelectricity	[p_i]	1	3	$\Delta P_i = p_i \cdot \Delta T$	[P_i] dielectric polarization	T temperature
Electrocaloric effect	[p_i]	1	3	$\Delta S = p_i \Delta E_i$	$\Delta S$ entropy	[E_i] electric field
Dielectric permittivity	$[\varepsilon_{ij}]$	2	6	$D_i=\varepsilon_{ij}E_j$	[D_i] electric displacement	[E_j] electric field
Magnetic permeability	$[\mu_{ij}]$	2	6	$B_i=\mu_{ij}H_j$	[B_i] magnetic induction	[H_j] magnetic field
Electrical conductivity	$[\sigma_{ik}]$	2	6	$j_i=\sigma_{ik}E_k$	[j_i] current density	[E_k] electric field
Electrical resistivity	$[\rho_{ik}]$	2	6	$E_i=\rho_{ik}\cdot j_k$	[E_i] electric field	[j_k] current density
Thermal conductivity	[k_ij]	2	6	$h_i=-k_{ij}(\partial T / \partial x_j)$	[h_i] heat flux	$[\partial T /\partial x_j]$ temperature gradient
Thermal expansion	$[\alpha_{ij}]$	2	6	$\varepsilon_{ij}=\alpha_{ij}\Delta T$	$[\varepsilon_{ij}]$ strain	T temperature
Seebeck effect	$[\beta_{ik}]$	2	9	$E_i=-\beta_{ik}(\partial T/\partial x_k)$	[E_i] electric field	$[\partial T/\partial x_k]$ temperature gradient
Peltier effect	$[\pi_{ik}]$	2	9	$h_i=\pi_{ik}j_k$	[h_i] heat flux	[j_k] current density
Hall effect	$\rho_{ikl}]$	3	9	$E_i=\rho_{ikl}\cdot j_k\cdot H_l$	[E_i] electric field	[j_k] current density [H_l] magnetic field
Direct piezoelectric effect	[d_ijk]	3	18	$P_i = d_{ijk}\cdot\sigma_{jk}$	[P_i] dielectric polarization	$[\sigma_{jk}]$ stress
Converse piezoelectric effect	[d_ijk]	3	18	$\varepsilon_{jk}=d_{ijk}E_i$	$[\varepsilon_{jk}]$ strain	[E_i] electric field
Piezomagnetic effect	[q_lij]	3	18	$M_l=q_{lij}\sigma_{ij}$	[M_l] magnetic polarization	$[\sigma_{ij}]$ stress
Electro-optical effect	[r_ijk]	3	18	$\Delta a_{ij}=r_{ijk}E_k$	[a_ij] dielectric impermeability	[E_k] electric field
Second harmonic generation	[d_ijk]	3	18	$P_i^{2\omega}=d_{ijk}E_jE_k$	$[P_i^{2\omega}]$ dielectric polarization at frequency $2\omega$	$[E_j],\,[E_k]$ electric field
Second-order elastic stiffnesses	[c_ijkl]	4	21	$\sigma_{ij}=c_{ijkl}\varepsilon_{kl}$	$[\sigma_{ij}]$ stress	$[\varepsilon_{kl}]$ strain
Second-order elastic compliances	[s_ijkl]	4	21	$\varepsilon_{ij}=s_{ijkl}\sigma_{kl}$	$[\varepsilon_{ij}]$ strain	$[\sigma_{kl}]$ stress
Piezooptic effect	$[\pi_{ijkl}]$	4	36	$\Delta a_{ij}= \pi_{ijkl}\sigma_{kl}$	[a_ij] dielectric impermeability	$[\sigma_{kl}]$ stress
Quadratic electrooptic effect	[R_ijkl]	4	36	$\Delta a_{ij}= R_{ijkl}E_kE_l$	[a_ij] dielectric impermeability	$[E_k],\,[E_l]$ electric field
Electrostriction	$[\gamma_{iljk}]$	4	36	$\varepsilon_{jk}=\mu_{iljk}E_iE_l$	$[\varepsilon_{jk}]$ strain	$[E_i],\,[E_l]$ electric field
Third-order elastic stresses	[c_ijklmn]	6	56	$\Phi=\frac{1}{2}c_{ijkl}\cdot \eta_{ij}\cdot\eta_{kl} + \frac{1}{6}c_{ijklmn}\cdot\eta_{ij}\cdot\eta_{kl}\cdot\eta_{mn}]$	$\Phi$ energy of deformation [c_ijkl] second-order stiffnesses	$[\eta_{ij}],\,[\eta_{kl}],\,[\eta_{mn}]$ the Lagrange finite strain components

3. The intrinsic symmetry of the physical properties

The rank of the tensors determines the numbers of the tensor components. The number of the components of the 0,1,2,3,4,5,6-rank tensors are 1,3,9,27,81,243,729. However, certain symmetries considerably reduce the number of the independent components. These may be intrinsic symmetries, inherent in the physical property, or crystal symmetries, whose effect on the number of the independent components will be discussed in the next section.

In some instances the intrinsic symmetries follow from the definition of the physical property in question. Thus for example in the case of elasticity it follows from the symmetry of the stress and deformation tensors that also the fourth-rank tensor of the second-order elastic stiffnesses [c_ijkl] (see Table 1) is symmetric with respect to the (ij) and (kl) permutations. This way the number of the independent coefficients of the fourth-rank elastic tensor decreases from 81 to 36. Further on from the symmetry of the deformation tensor follows the symmetry of the [d_ijk] piezo-electric tensor (see Table 1) with respect to the commutability of the j and k suffixes, which means that the piezoelectric tensor has not more than 18 independent components.

The symmetries inherent in the physical properties may be in most cases found by thermodynamical reasoning. In case of equilibrium properties, i.e. properties which refer to thermodynamically reversible changes, the intrinsic symmetry of the properties can be disclosed by investigating the thermodynamical potentials. For physical properties characteristic for transport processes the intrinsic symmetry is the consequence of Onsager's principle.

In order to illustrate the thermodynamical discussion of equilibrium properties let us consider a more complicated example from which not only the symmetry of the tensors representing individual physical properties (tensors of elasticity, electric and magnetic susceptibility) but also the relationship among the tensors representing various properties becomes obvious. In the example the elastic, thermo, electric and magnetic effects are investigated simultaneously. Independent variables should be the stress [ $\sigma_{kl}$ ], the electric field [E_k], the magnetic field [H_l] and temperature [T] whereas the deformation [ $\varepsilon_{ij}$ ], the polarization [P_i], the magnetization [M_i] and the entropy [S] are selected as dependent variables. The differentials of the former quantities are obviously connected with the following relationships:

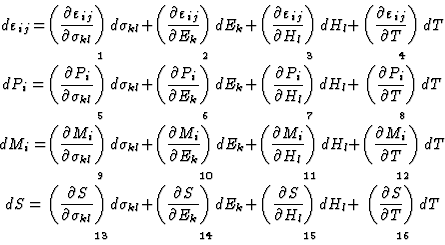$\begin{displaymath} \begin{array} {@{}c@{}c@{}c@{}c@{}c@{}c} d\varepsilon_{ij} =... ...style13&\scriptstyle14&\scriptstyle15&\scriptstyle16\end{array}\end{displaymath}$

(3.1)

The partial derivatives are characteristic of the following effects:

1. Elastic deformation.

2. Reciprocal (or converse) piezo-electric effect.

3. Reciprocal (or converse) piezo-magnetic effect.

4. Thermal dilatation.

5. Piezo-electric effect.

6. Electric polarization.

7. Magneto-electric polarization.

8. Pyroelectricity.

9. Piezo-magnetic effect.

10. Reciprocal (or converse) magneto-electric polarization.

11. Magnetic polarization.

12. Pyromagnetism.

13. Piezo-caloric effect.

14. Electro-caloric effect.

15. Magneto-caloric effect.

16. Heat transmission.

In order to recognize the relationships among the partial derivatives of the equation-system (3.1) let us discuss the Gibb's potential of the system

$\begin{displaymath} G = U - \sigma_{ij}\varepsilon_{ij} - E_kP_k - H_lM_l - TS. \end{displaymath}$

(3.2)

Remembering that the total differential of the internal energy according to the first and second law of thermodynamics is

$\begin{displaymath} dU = \sigma_{ij} d\varepsilon_{ij} + E_k dP_k + H_l dM_l + T dS\end{displaymath}$

(3.3)

one obtains for the total differential of the Gibbs' potential the expression

$\begin{displaymath} dG = -\varepsilon_{ij}d\sigma_{ij} - P_k dE_k - M_l dH_l - S dT.\end{displaymath}$

(3.4)

At the same time one may describe the total differential of the Gibbs' potential with the partial derivatives of the independent variables:

$\begin{displaymath} dG = \left(\frac{\partial{G}}{\partial\sigma_{ij}}\right) d\... ...l}\right)dH_l + \left(\frac{\partial{G}}{\partial{T}}\right)dT \end{displaymath}$

(3.5)

that is

$\begin{displaymath} \left(\frac{\partial{G}}{\partial\sigma_{ij}}\right) = - \varepsilon_{ij} \end{displaymath}$

(3.6)

$\begin{displaymath} \left(\frac{\partial{G}}{\partial{E}_k}\right) = -P_k \end{displaymath}$

(3.7)

$\begin{displaymath} \left(\frac{\partial{G}}{\partial{H}_l}\right) = -M_l \end{displaymath}$

(3.8)

$\begin{displaymath} \left(\frac{\partial{G}}{\partial{T}}\right) = -S. \end{displaymath}$

(3.9)

Investigating the second partial derivatives of the Gibbs' potential and taking into consideration the commutability of the sequence of the partial differentiations one comes to the conclusion that the elastic [s_ijkl], dielectric [ $\chi_{jk}$ ] and diamagnetic susceptibility [ $\psi_{kl}$ ] tensors, as defined by eqs. (3.10)-(3.12) below, are symmetrical

$\begin{displaymath} - \left(\frac{\partial^2{G}}{\partial\sigma_{kl}\partial\sig... ...= \frac{\partial\varepsilon_{kl}}{\partial\sigma_{ij}}=s_{klij}\end{displaymath}$

(3.10)

$\begin{displaymath} -\left(\frac{\partial^2{G}}{\partial{E}_j\partial{E}_k}\righ... ...E}_j}\right) = \frac{\partial{P}_j}{\partial{E}_k} = \chi_{jk} \end{displaymath}$

(3.11)

$\begin{displaymath} -\left(\frac{\partial^2{G}}{\partial{H}_k\partial{H}_l}\righ... ...}_k}\right) = \frac{\partial{M}_k}{\partial{H}_l} = \psi_{kl}. \end{displaymath}$

(3.12)

Moreover, the study of the partial derivatives not only demonstrates the symmetry of the above tensors, but also indicates that the components of the tensors representing the direct and reciprocal effects correspond to each other. Let us investigate the following partial derivatives

$\begin{displaymath} - \left(\frac{\partial^2{G}}{\partial\sigma_{ij}\partial{E}_... ...rac{\partial \varepsilon_{ij}}{\partial{E}_k}\right) = d_{kij} \end{displaymath}$

(3.13)

$\begin{displaymath} -\left(\frac{\partial^2{G}}{\partial\sigma_{ij}\partial{H}_l... ...frac{\partial \varepsilon_{ij}}{\partial{H}_l}\right)= q_{lij} \end{displaymath}$

(3.14)

$\begin{displaymath} - \left(\frac{\partial^2{G}}{\partial{E}_k\partial{H}_l}\rig... ...\left(\frac{\partial{P}_k} {\partial{H}_l}\right)=\lambda_{lk} \end{displaymath}$

(3.15)

$\begin{displaymath} - \left(\frac{\partial^2{G}}{\partial\sigma_{ij}\partial{T}}... ...rac{\partial \varepsilon_{ij}}{\partial{T}}\right)=\alpha_{ij} \end{displaymath}$

(3.16)

$\begin{displaymath} -\left(\frac{\partial^2{G}}{\partial{T}\partial{E}_k}\right)... ...T}}\right)=\left(\frac{\partial{S}} {\partial{E}_k}\right)=p_k \end{displaymath}$

(3.17)

$\begin{displaymath} -\left(\frac{\partial^2{G}}{\partial{T}\partial{H}_l}\right)... ...}}\right)=\left(\frac{\partial{S}} {\partial{H}_l}\right)=m_l. \end{displaymath}$

(3.18)

From the above equations follows that correspondences exist between:

(a) the components of the tensors representing the piezoelectric and reciprocal piezo-electric effect (eq. 3.13)),

(b) the components of the tensors representing the piezo-magnetic and reciprocal piezo-magnetic effect (eq. (3.14)),

(c) the components of the tensors representing the magneto-electric polarization and reciprocal magneto-electric polarization (eq. (3.15)),

(d) the components of the tensors representing the piezo-caloric effect and the thermal dilatation (eq. (3.16)),

(e) the components of the tensors representing the pyroelectric and electrocaloric effect (eq. (3.17)),

(f) the components of the tensors representing the pyromagnetic and magneto- caloric effect (eq. (3.18)).

Integrating equations (3.1) taking into consideration the above statements, and restricting only to the first-order effects, the following system of equations is obtained

$\begin{displaymath} \varepsilon_{ij}=s_{ijkl}\sigma_{kl}+d_{kij}E_k+q_{lij}H_l+\alpha_{ij}\Delta{T}\end{displaymath}$

$\begin{displaymath} P_k = d_{kij}\sigma{ij}+\chi_{kl}E_l+\lambda_{lk}H_l+p_k\Delta{T}\end{displaymath}$

(3.19)

$\begin{displaymath} M_l = q_{lij}\sigma_{ij}+\lambda_{lk}E_k+\psi_{lm}H_m+m_l\Delta{T}\end{displaymath}$

$\begin{displaymath} \Delta{S} = \alpha_{ij}\sigma_{ij}+p_kE_k+m_lH_l+\frac{c}{T}\Delta{T} \qquad (i,j,k,l = 1, 2, 3).\end{displaymath}$

It is perhaps worthwhile to draw the reader's attention to the fact that the system of equations (3.19) represents 16 = 9 + 3 + 3 + 1 equations, the right side of these equations contains 16 terms, since the suffixes occurring twice in each term imply summation according to the Einstein convention. Furthermore the deformation tensor [ $\varepsilon_{ij}$ ] and the stress tensor [ $\sigma_{kl}$ ]are symmetrical, consequently the system of equation (3.19) contains altogether 13 independent equations with 13 independent variables.

As has been pointed out the intrinsic symmetry characteristic for the transport processes is the consequence of Onsager's reciprocal relations. However, it is important to stress that this relation is valid only if the fluxes and the thermodynamical forces connected with them are suitably selected. For simplicity let us study the case of the electrical conductivity. The thermodynamical force [X_k] attached to the electrical current density [j_i] is

$\begin{displaymath} X_k = \frac{1}{T} \frac{\partial\Phi}{\partial{x}_k} \qquad (k = 1, 2, 3) \end{displaymath}$

(3.20)

where $\partial\Phi/\partial{x}_k$ denotes the k-th component of the $\Phi$ electrical potential gradient and T is the temperature.

In this case the law of linear current flow is

$\begin{displaymath} j_i = L_{ik} \frac{1}{T}\frac{\partial\Phi}{\partial{x}_k} \qquad (i,k = 1, 2,3). \end{displaymath}$

(3.21)

The expanded form of this equation will be

$\begin{displaymath} j_1 = L_{11}\frac{1}{T} \frac{\partial\Phi}{\partial{x}_1}+L... ...tial{x}_2}+L _{13}\frac{1}{T}\frac{\partial\Phi}{\partial{x}_3}\end{displaymath}$

$\begin{displaymath} j_2 = L_{21}\frac{1}{T}\frac{\partial\Phi}{\partial{x}_1}+L_... ...rtial{x}_2}+L_{23}\frac{1}{T}\frac{\partial\Phi}{\partial{x}_3}\end{displaymath}$

(3.22)

$\begin{displaymath} j_3 = L_{31}\frac{1}{T}\frac{\partial\Phi}{\partial{x}_1}+L_... ...ial{x}_2}+L_{33}\frac{1}{T}\frac{\partial\Phi}{\partial{x}_3}. \end{displaymath}$

According to Onsager's reciprocity relation the L_ik conductivity coefficients are symmetrical with respect to the interchangeability of the suffices, i.e.

L_ik = L_ki.

(3.23)

The relationship between the conductivity coefficients and the components of the specific conductivity tensor [ $\sigma_{ik}$ ] are easily found. The defining equation of the [ $\sigma_{ik}$ ] tensor (see Table 1), is

$\begin{displaymath} j_i = \sigma_{ik}E_k = -\sigma_{ik}\frac{\partial\Phi}{\partial{x}_k}. \end{displaymath}$

(3.24)

However by comparing equations (3.21) and (3.24) one readily sees that

$\begin{displaymath} L_{ik} = -T\sigma_{ik}. \end{displaymath}$

(3.25)

From eqs. (3.23) and (3.25) on the other hand the symmetry of the tensor representing the specific electrical conductivity is quite obvious.

Discussing composite transport processes by some proper selection of the fluxes and thermodynamical forces corresponding to them not only the symmetry of the various tensors, but also the relationships among the tensors representing various properties follow from Onsager's reciprocity relations. For example when discussing the thermoelectric effects the symmetry of the electrical and thermal conductivity tensors follow from Onsager's principle as well as the relationships between the tensors representing the Seebeck effect [ $\beta_{ik}$ ]and the Peltier tensor [ $\pi_{ik}$ ] (see Table 1).

$\begin{displaymath} T \cdot \beta_{ik} = \pi_{ik}. \end{displaymath}$

(3.26)

Additionally it should be remarked that the relationship between the conductivity coefficients in the presence of ( $\=H$ ) magnetic field takes the form

$\begin{displaymath} L_{ik}(\=H) = L_{ki}(-\=H). \end{displaymath}$

(3.27)

4. Neumann's principle

It has been demonstrated in the previous section that the intrinsic symmetry of the physical properties decreases the number of the independent tensor components. Further reduction of the independent components of a physical property tensor, and the zero value of certain components follow from the fact that the crystal symmetry exerts some influence on the symmetry of the physical properties. This fact is expressed by Neuman's principle formulated already in the 19th century according to which the symmetry elements of any physical property of a crystal must include all the symmetry elements of the point group of the crystal :

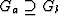$\begin{displaymath} G_a \supseteq G_k\end{displaymath}$

(4.1)

where G_k denotes the symmetry group of the crystal, G_a is the symmetry group of the tensor representing the physical property, the sign $\supset$ indicates that the subgroup belongs to the group. The symmetry group of the crystal refers generally to the 32 point groups derived from the crystal forms, however, sometimes also the recently introduced 90 magnetic or more generally the 122 Shubnikov groups (see [10-14]) should be considered. According to Neumann's principle the tensor representing any physical property should be invariant with regard to every symmetry operation of the given crystal class. The condition of invariance reduces the number of the independent tensor components, since it signifies relationships between the tensor components. In order to describe these relationships it is necessary to discuss the transformation of the tensor components to some extent.

The well-known equations of transformation from an orthogonal x₁, x₂, x₃ system to another similarly orthogonal $x^{\prime}_1, x^{\prime}_2, x^{\prime}_3$ system are for first-, second-, third- and fourth-rank polar tensors according to their definition:

$\begin{displaymath} T^{\prime}_i = a_{ij}T_{j} \end{displaymath}$

(4.2)

$\begin{displaymath} T^{\prime}_{ij} = a_{ik}a_{jl}T_{kl} \end{displaymath}$

(4.3)

$\begin{displaymath} T^{\prime}_{ijk} = a_{il}a_{jm}a_{kn}T_{lmn} \end{displaymath}$

(4.4)

$\begin{displaymath} T^{\prime}_{ijkl} = a_{im}a_{jn}a_{ko}a_{lp}T_{mnop} \end{displaymath}$

(4.5)

which leads us to the general polar-tensor transformation notation expressed in the equation:

$\begin{displaymath} T^{\prime}_{ijk...n} = a_{ip}a_{jq}a_{kr}\dots a_{nu}T_{pqr...u} \end{displaymath}$

(4.6)

where the a_ij direction cosines are the elements of the (a_ij) matrix. The (a_ij) matrix connects the original and the 'new' co-ordinates according to the matrix equation

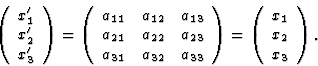$\begin{displaymath} \left(\begin{array} {c} x^{\prime}_1\\ x^{\prime}_2\\ x^{\pr... ...ght)=\left(\begin{array} {c}x_1\\ x_2\\ x_3\end{array}\right). \end{displaymath}$

(4.7)

In some cases the tensor describing the physical properties is not polar, but axial (as for instance the tensor describing the optical activity or piezomagnetism). For axial (or pseudo) tensors the following transformation relation may be used as definition

$\begin{displaymath} T^{\prime}_{ijk...n} = \vert a_{ij}\vert a_{ip}a_{jq}a_{kr}\dots a_{nu}T_{pqr...u} \end{displaymath}$

(4.8)

where |a_ij| denotes the value of the determinant of the matrix (a_ij) whose value is (+1) if the transforming operation consists of pure rotation and (-1) if besides rotation the transformation contains also an inversion, which means that the symmetry operation changes also the hand of the axes.

It is not difficult to find out whether the tensor representing any physical property is polar or axial, since this can be easily decided by the eq. (2.1) defining the physical property in question. If only one of the tensors [A_pqr...u] and [B_ijk...n] in eq. (2.1) is axial (for instance magnetic field is an axial tensor of rank one) also the property tensor [a_{ijk...npqr...u}] as defined by eq. (2.1) will be axial, in every other case the tensor is polar.

It should be remarked that if also the magnetic point groups are considered eq. (4.6) and eq. (4.8) expressing the transformation properties of the tensor components are valid only for conventional symmetry operations. If, however, the conventional symmetry operations are combined with time-inversion which actually happens in anti-symmetry operations (see [10-14]) the right sides of eqs. (4.6) and (4.8) respectively should be multiplied with (-1) whenever eq. (2.1) defining the physical properties contains the magnetic vector quantities (magnetic field, magnetic induction, magnetization vector) odd times. Tensors representing this type of properties are called C-tensors.¹ For a more detailed discussion of this problem the reader is referred to the literature.^1-3

Considering the equations of transformation (4.6) and (4.8) and with regard to the above remark, the relationships between the components of the polar and axial tensors for a given crystal class can now be defined, since the invariance of a tensor with regard to any symmetry operation requires the relationship

$\begin{displaymath} T^{\prime}_{ijk...n} = T_{ijk...n}. \end{displaymath}$

(4.9)

Thus in case of polar tensors, if the matrix (a_ij) describes any conventional symmetry operation of a given crystal class, the tensor components must according to the Neumann's principle satisfy the equation

$\begin{displaymath} T_{ijk...n} = a_{ip}a_{jq}a_{kr}\dots a_{nu}T_{pqr...u} \end{displaymath}$

(4.10)

whereas considering the condition of the invariance of axial tensors taking into account the eqs. (4.8) and (4.9) one may write

$\begin{displaymath} T_{ijk...n} = \vert a_{ij}\vert a_{ip}a_{jq}a_{kr}\dots a_{nu}T_{pqr...u} \end{displaymath}$

(4.11)

Of course in the case of antisymmetry operations and the previously discussed C-tensors the right-hand side of the eqs. (4.10) and (4.11) are multiplied with (-1).

For every tensor component an equation of the type (4.10) and (4.11) respectively should be valid so that the tensor components must satisfy a system of these equations. Since this holds for every symmetry operation of a given crystal class, the number of the systems of equations between the tensor components will be equal to the number of the symmetry operations which may be performed in the given crystal class. However, in order to obtain every relationship among the components of a tensor representing any physical property in case of a given crystal class, it is not necessary to write down for every symmetry operation the system of equations of the type (4.10) and (4.11) respectively. It is well known from the group theory that for various crystal classes every symmetry operation may be deduced from a few basic symmetry operations. The application of the matrices corresponding to these basic operations (the generating matrices) are sufficient to obtain the effect due to the symmetry of a crystal class on the given tensor in question. Tables 2 and 3 summarize a series of generating matrices for every conventional crystal class.

These interrelations appear to be at first instance somewhat complicated, a simple example, however, will help to obtain a better understanding. Let us consider the form of the pyroelectric tensor in the crystal class 3 of the trigonal system assuming that the x₃ axis of the coordinate system is the three-fold rotation axis. As one may see on consulting Tables 2 and 3 the coordinate transformation related to the symmetry operation can be described with the following matrix

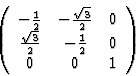$\begin{displaymath} \left(\begin{array} {ccc} -\frac{1}{2}&-\frac{\sqrt{3}}{2}&0\\ \frac{\sqrt{3}}{2}&-\frac{1}{2}&0\\ 0&0&1\end{array}\right) \end{displaymath}$

(4.12)

Taking into consideration the condition of invariance of the polar tensor as expressed in eq. (4.10) one obtains for the tensor components the following equations

$\begin{displaymath} p_1 = -\frac{1}{2}p_1-\frac{\sqrt{3}}{2}p_2\end{displaymath}$

$\begin{displaymath} p_2=\frac{\sqrt{3}}{2}p_1-\frac{1}{2}p_2\end{displaymath}$

(4.13)

p₃=p₃.

It follows from these equations that p₁ = p₂ = 0 and only p₃ can differ from zero, consequently the form of the pyroelectric tensor of crystal class 3 of the trigonal system will be p = [0; 0; p₃].

**Table 2:** The generating matrices of the 32 point groups (crystal classes). After Koptsik¹³

Crystal system	Class symbol		Generating matrices	No. of symmetry elements	The choice of x₁, x₂, x₃ crystal physical axes in relation to the symmetry axes

	International	Schoenflies

Triclinic	1	C₁	M₀	1
	$\=1$	S₂=C_i	M₁	2
Monoclinic	2	C₂	M₂	2
	m	C_1h=C_s	M₃	2	$x_3 \parallel 2 \mbox{ or }\=2$
	2/m	C_2h	M₂, M₃	4
Orthorhombic	222	V=D₂	M₄, M₂	4	$x_1 \parallel 2\mbox{ or }\=2$
	mm2	C_2v	M₅, M₂	4	$x_2 \parallel 2\mbox{ or }\=2$
	mmm	V_h=D_2h	M₅, M₆, M₃	8	$x_3 \parallel 2$
Tetragonal	4	C₄	M₇	4
	$\=4$	S₄	M₈	4
	422	D₄	M₇, M₄	8	$x_1 \parallel 2\mbox{ or }\=2$
	4/m	C_4h	M₇, M₃	8	$x_2 \parallel 2\mbox{ or }\=2$
	4mm	C_4v	M₇, M₅	8	$x_3 \parallel 4\mbox{ or }\=4$
	$\=42m$	V_d=D_2d	M₈, M₄	8
	4/mmm	D_4h	M₇, M₃, M₅	16
Trigonal	3	C₃	M₉	3
	$\=3$	S₆=C_3i	M₁₀	6	$x_1 \parallel 2\mbox{ or }\=2$
	32	D₃	M₉, M₄	6	$x_2 \perp 2\mbox{ or }\=2$
	3m	C_3v	M₉, M₅	6	$x_3 \parallel 3\mbox{ or }\=3$
	$\=3m$	D_3d	M₁₀, M₅	12
Hexagonal	6	C₆	M₁₁	6
	$\=6$	C_3h	M₁₂	6
	$\=6m2$	D_3h	M₁₂, M₅	12	$x_1 \parallel 2\mbox{ or }\=2$
	622	D₆	M₁₁, M₄	12	$x_2 \perp 2\mbox{ or }\=2$
	6/m	C_6h	M₁₁, M₃	12	$x_3 \parallel 6 \mbox{ or }\=6$
	6/mm	C_6v	M₁₁, M₅	12
	6/mmm	D_6h	M₁₁, M₅, M₃	24
Cubic	23	T	M₁₃, M₂	12	$x_1 \parallel 2$
	m3	T_h	M₁₄, M₂	24	$x_2 \parallel 2, x_3 \parallel 2$
	432	O	M₁₃, M₇	24	$x_1 \parallel 4\mbox{ or }\=4$
	$\=43m$	T_d	M₁₃, M₈	24	$x_2 \parallel 4\mbox{ or }\=4$
	m3m	O_h	M₁₄, M₇	48	$x_3 \parallel 4\mbox{ or }\=4$

**Table 3:** Generating matrices

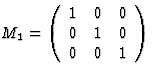	identity

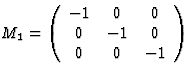inversion		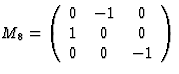fourfold inversion-rotation about x₃ axis
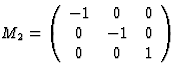twofold rotation about x₃ axis		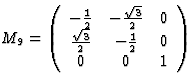threefold rotation about x₃ axis
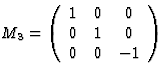reflection in x₁x₂ plane		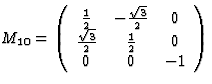threefold inversion-rotation about x₃ axis
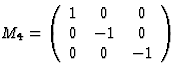twofold rotation about x₁ axis		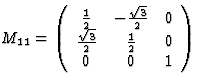sixfold rotation about x₃ axis
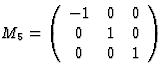reflection in x₂x₃ plane		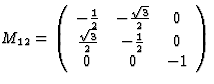sixfold inversion-rotation about x₃ axis
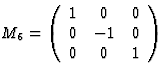reflection in x₁x₃ plane		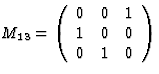threefold rotation about [111] direction
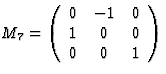fourfold rotation about x₃ axis		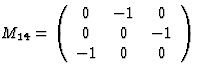threefold inversion-rotation about [111] direction

The method used in this example may be applied in every case, though with higher rank tensors it may be in many cases rather tiresome.

Considerable time can be saved (with the exception of the trigonal and hexagonal classes) by the direct inspection method worked out by Fumi,⁴, which though in principle not differing from the previous treatment leads to results in a relatively short time. Fumi's method is based on the fact that in an orthogonal coordinate system the polar tensor components transform in the same way as the products of the corresponding coordinates (see eq. (4.6)). One must, however, be careful not to commute the sequence of the factors, thus for instance instead of the product x₁x₂ one cannot write x₂x₁.

Fumi's method may be studied by a simple example considering the form of a polar second-rank tensor, e.g. the dielectric susceptibility tensor of the crystal class 2 of the monoclinic system. Assuming that the two-fold symmetry axis coincides with the x₂ coordinate axis the symmetry operator will transform the coordinates in the following way

$\begin{displaymath} x_1 \rightarrow -x_1 \qquad x_2 \rightarrow x_2 \qquad x_3 \rightarrow -x_3\end{displaymath}$

(4.14)

or in a more concise way

$\begin{displaymath} 1 \rightarrow -1 \qquad 2 \rightarrow 2 \qquad 3 \rightarrow -3\end{displaymath}$

(4.15)

From this it follows that

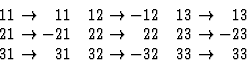$\begin{displaymath} \begin{array} {ccc} 11 \rightarrow \phantom{-}11 & 12 \right... ... & 32 \rightarrow -32 & 33 \rightarrow \phantom{-}33\end{array}\end{displaymath}$

(4.16)

that is

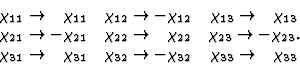$\begin{displaymath} \begin{array} {ccc} \chi_{11} \rightarrow \phantom{-}\chi_{1... ...i_{32} & \chi_{33} \rightarrow \phantom{-}\chi_{33}\end{array} \end{displaymath}$

(4.17)

At the same time as a consequence of Neumann's principle every component should be transformed into itself therefore

$\begin{displaymath} \begin{array} {cc} \chi_{12} = -\chi_{12} = 0 & \chi_{21} = ... ...{23} = -\chi_{23} = 0 & \chi_{32} = -\chi_{32} = 0.\end{array} \end{displaymath}$

(4.18)

Thus for class 2 of the monoclinic system the electric susceptibility tensor has the form

$\begin{displaymath} \left[\begin{array} {ccc} \chi_{11} & 0 & \chi_{13}\\ 0 & \chi_{22} & 0\\ \chi_{31} & 0 & \chi_{33}\end{array}\right]\end{displaymath}$

(4.19)

In the case of dielectric susceptibility as a result of the intrinsic symmetry $\chi_{31}$ is equal to $\chi_{13}$ i.e. the tensor (4.19) is symmetrical.

The forms of tensors or matrices composed of tensor components for the various crystal classes can be found properly tabulated in the special literature, see for example [1, 2, 5-7, 16, 17].

Finally it should be observed that in some cases simple geometric considerations enable the determination of the independent components of the tensors representing the physical properties. It is easy to see that no pyroelectric effect can exist in a crystal possessing a centre of symmetry. This means that for these crystals every component of the pyroelectric tensor is zero, p = [0, 0, 0], because in these crystals if the vector of polarization were pointed in a given direction the vector should appear also in the opposite direction as a result of Neumann's principle, consequently its value can only be zero.

5. The value of a physical property in a given direction

One frequently finds data in the literature which give the value of some physical property in a given direction. In this chapter the concept of the magnitude of a physical property in a given direction, and also the relationship between this value and the respective tensor components will be illustrated on the examples of the direction dependence of the electrical conductivity and Young's modulus respectively.

The specific conductivity in the direction of the electric field is defined as the ratio of the component parallel with the electric field of the current density ( $j_{\parallel}$ ) and the magnitude of the electric field (E), i.e. $j_{\parallel}/E$ . Let the components of the electric field be E_i = En_i, where n_i denotes the i-th component of the unit vector ( $\={n}$ ) pointing into the direction of the electric field. The component of the j current density parallel with $\=E$ is in tensor notation

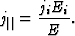$\begin{displaymath} j_{\parallel} = \frac{j_iE_i}{E}. \end{displaymath}$

(5.1)

Consequently the specific electric conductivity in the direction given by the unit vector $\={n}$ will be

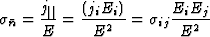$\begin{displaymath} \sigma_{\={n}}=\frac{j_{\parallel}}{E}=\frac{(j_iE_i)}{E^2}=\sigma_{ij}\frac{E_i E_j}{E^2}\end{displaymath}$

(5.2)

for which one has

$\begin{displaymath} \sigma_{\={n}} = \sigma_{ij} \cdot n_i \cdot n_j. \end{displaymath}$

(5.3)

Thus formula (5.3) yields the relationship between the value of the electrical conductivity in the direction of $\={n}$ and the components of the electrical conductivity tensors. Similar relationships give the value of the physical properties which can be represented by a second-rank tensor (e.g. thermal conductivity, dielectric permittivity, thermal expansion) in a given direction of a crystalline medium.

Equation (5.3) may be applied in two ways. One possibility is to calculate the tensor components from the measured conductivity values and the corresponding direction cosines. For this purpose one should measure the electrical conductivity in different directions, which are not connected by symmetry, as many times as the number of the independent components. Another possibility of applying eq. (5.3) is quite opposite to the first one. With the aid of the already known tensor components the conductivity value can be computed for any direction.

Equation (5.3) becomes considerably simplified for crystals of the tetragonal, trigonal and hexagonal systems which have only two independent tensor-components ( $\sigma_{11} = \sigma_{22}$ and $\sigma_{33}$ )

$\begin{displaymath} \sigma_n = \sigma_{11}n^2_1 + \sigma_{22}n^2_2 + \sigma_{33}n^2_3 = \sigma_{11}(1-n^2_3) + \sigma_{33}n^2_3. \end{displaymath}$

(5.4)

If the angle between the $\={n}$ vector and the x₃ principal axis of the crystal is denoted by $\theta$ the following equation is obtained

$\begin{displaymath} \sigma_{\={n}} = \sigma_{11}\sin^2 \theta + \sigma_{33}\cos^2 \theta.\end{displaymath}$

(5.5)

The component $\sigma_{33}$ is frequently denoted as $\sigma_{\parallel}$ and the component of $\sigma_{11}$ as $\sigma_{\perp}$ with reference to the conductivity values parallel with the main axis of the crystal (i.e. with the three-, four- or six-fold axis) and vertical to this axis resp. With these notations Eq. (5.5) may be rewritten to obtain

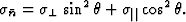$\begin{displaymath} \sigma_{\={n}}=\sigma_{\perp}\sin^2 \theta + \sigma_{\parallel}\cos^2 \theta.\end{displaymath}$

(5.6)

As another example we will study the direction dependence of Young's modulus. To begin with it should be stated that Young's modulus in the pulling direction is defined as the ratio of the longitudinal stress ( $\sigma_{ii}$ ) and the longitudinal strain ( $\varepsilon_{ii})$ . If the $x^{\prime}_3$ axis of the coordinate system is placed in the direction of the $\={n}$ unit vector Young's modulus in this direction will apparently be

$\begin{displaymath} E_{\={n}{\parallel}x^{\prime}_3} = \frac{\sigma^{\prime}_{33}}{\varepsilon^{\prime}_{33}}. \end{displaymath}$

(5.7)

According to eq. (3.19) (if no external field exists)

$\begin{displaymath} \varepsilon^{\prime}_{33} = s^{\prime}_{3333}\sigma^{\prime}_{33} \end{displaymath}$

(5.8)

and one obtains

$\begin{displaymath} E_{\={n}{\parallel}x^{\prime}_3} = \frac{1}{s^{\prime}_{3333}}. \end{displaymath}$

(5.9)

Consequently in order to find the direction dependence of Young's modulus it is necessary to know the change of the tensor-component $s^{\prime}_{3333}$ in the various directions. This dependence, however, is given by the (4.5) transformation equation of the $s^{\prime}_{3333}$ tensor component.

$\begin{displaymath} s^{\prime}_{3333} = a_{3i} \cdot a_{3j} \cdot a_{3k} \cdot a_{3l} \cdot s_{ijkl}\end{displaymath}$

(5.10)

where a_3i, a_3j, a_3k, a_3l denote the direction cosines of the $x^{\prime}_3$ axis parallel with the $\={n}$ unit vector with respect to the crystalphysical co-ordinate system; consequently

$\begin{displaymath} s^{\prime}_{3333} = n_i \cdot n_j \cdot n_k \cdot n_l \cdot s_{ijkl}. \end{displaymath}$

(5.11)

From this equation and eq. (5.9) one obtains Young's modulus of the crystals belonging to the cubic system

$\begin{displaymath} E_{\={n}} = \frac{1}{s_{1111} -2(s_{1111} -s_{1122} - 2s_{2323})(n^2_1n^2_2+n^2_2n^2_3+n^2_3n^2_1)}. \end{displaymath}$

(5.12)

This means that even in the case of cubic crystals Young's modulus is direction dependent.

6. Higher order effects

The relationship between two physical properties is not necessarily linear. The relation between the dependent and independent physical variables can be often expressed with Taylor expansion. Thus for instance the electric field dependence of the electric polarization in a strong field is described with expansion in power series

$\begin{displaymath} P_i = \chi^0_{ij}E_j + \chi_{ijk}E_jE_k + \chi_{ijkl}E_jE_kE_l + \cdots \end{displaymath}$

(6.1)

where the tensor [ $\chi^0_{ij}$ ] describes the linear or first-order effect, the tensor [ $\chi_{ijk}$ ] stands for the second-order effect and so on. (The second-order effect explains the generation of double frequency light waves whenever light passes through crystals without symmetry centres).

There is some freedom in deciding the order of an effect, which depends upon the aspect the effect is studied. Thus in the above example if instead of the tensor [ $\chi^0_{ij}$ ] the differential quotient with respect to the electric field of the electric polarization vector (i.e. the [ $\chi_{ij}$ ] tensor) is considered as dielectric susceptibility, the previously second-order effect may be regarded as a first-order effect, which describes the electric field dependence of the dielectric susceptibility. This becomes obvious from the equation

$\begin{displaymath} \frac{{\partial}P_i}{{\partial}E_j} = \chi_{ij} = \chi^0_{ij} + \chi_{ijk}E_k + \chi_{ijkl}E_kE_l. \end{displaymath}$

(6.2)

The dependence of the electrical resistivity on the magnetic field is similarly

$\begin{displaymath} \rho_{ik}(H) = \rho^0_{ik} + \rho_{ikl}H_l + \rho_{iklm}H_lH_m + \rho_{iklmn}H_lH_mH_n \end{displaymath}$

(6.3)

where the [ $\rho^0_{ik}$ ] tensor represents the electrical resistivity in the absence of a magnetic field; the tensor [ $\rho_{iklm}$ ] describes the change of electrical resistivity due to a magnetic field, and the tensors [ $\rho_{ikl}$ ]and [ $\rho_{iklmn}$ ] refer to the first- and second-order Hall effects.

Finally it should be noted that in the theory of elasticity the coefficients of the second-order effect are called third-order elastic stiffnesses, because it is more suitable to start the discussion of the nonlinear stress-deformation relationship with the energy function whose third-order derivatives supply the coefficients of the principally second-order effects.

7. Description of the physical properties in matrix notation

It has been shown in the previous sections that the various physical properties of the crystals can be described quite suitably with tensors. However, especially with higher rank tensors the great number of suffixes may become inconvenient. In many cases the introduction of a new notation, the matrix notation, is suitable to reduce the number of suffixes. The introduction of the matrix notation may be encouraged by the usually considerable reduction, due to intrinsic symmetries, of the number of independent components of the tensors representing the physical properties.

Let us consider first a simple example. For some purpose the following ( $\alpha_i$ ) matrices are formed from the components of the symmetrical second rank [ $\alpha_{ij} = \alpha_{ji}$ ] tensor

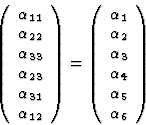$\begin{displaymath} \left(\begin{array} {c} {\alpha}_{11}\\ {\alpha}_{22}\\ {\al... ...ha}_3\\ {\alpha}_4\\ {\alpha}_5\\ {\alpha}_6\end{array}\right) \end{displaymath}$

(7.1)

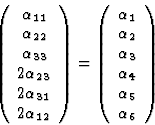$\begin{displaymath} \left(\begin{array} {c} \alpha_{11}\\ \alpha_{22}\\ \alpha_{... ...\\ \alpha_3\\ \alpha_4\\ \alpha_5\\ \alpha_6\end{array}\right) \end{displaymath}$

(7.2)

As can be easily noted from the formulae (7.1) and (7.2) in both cases the same tensor component is connected with the same matrix element, i.e. the relation between the suffixes of the tensor components and matrix terms is unambiguous

$\begin{displaymath} \begin{array} {lcccccc} \mbox{tensor suffixes} & 11 & 22 & 3... ...21 \\ \mbox{matrix suffixes} & 1 & 2 & 3 & 4 & 5 & 6\end{array}\end{displaymath}$

(7.3)

This way by introducing the matrix notation the number of the suffixes is reduced on the condition that the new suffixes beside 1, 2 and 3 can now take also the values 4, 5 and 6. Although the relationship between the suffixes of the tensor components and matrix elements is unambiguous, the relationship between the tensor components and the matrix elements is defined to the extent of a multiplication factor. A few examples explaining the role of this factor are given below.

The advantage of the matrix notation becomes obvious with the third and higher rank tensors. A third rank tensor, occurring rather frequently in crystal physics, is the piezo-electric tensor, which describes the relationship between the stresses effective on the crystal and the resulting electric polarization according to the equation

$\begin{displaymath} P_i = d_{ijk} \cdot \sigma_{jk} \qquad (i,j,k = 1,2,3).\end{displaymath}$

(7.4)

The number of the components of the third rank piezoelectric tensor is 3³ = 27, which means that the components could be written in a three dimensional cubic table where the layer would refer to the first suffix, the second suffix would be the row, and the third the column. However, considering that the [d_ijk] tensor is symmetric with respect to the commutability of the k and j suffixes (see paragraph 3) by introducing a new notation the number of these suffixes is reduced. The suffix pair jk can be substituted according to (7.3) by only one. The elements (d_in) of the piezoelectric matrix are formed from the [d_ijk] tensor components in the following way

$\begin{displaymath} \begin{array} {lcl} d_{in} = d_{ijk} & \mbox{ if } & n = 1, 2, 3 \\ d_{in} = 2d_{ijk} & \mbox{ if } & n = 4, 5, 6.\end{array}\end{displaymath}$

(7.5)

Once the notation of the piezoelectric matrix is accepted as above in (7.5) and a matrix is generated from the components of the stress tensor according to eq. (7.1) one obtains the following matrix equation

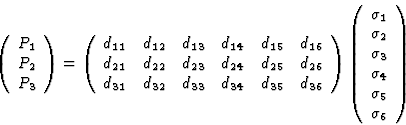$\begin{displaymath} \left(\begin{array} {c} P_1\\ P_2\\ P_3\end{array}\right)=\l... ...2\\ \sigma_3\\ \sigma_4\\ \sigma_5\\ \sigma_6\end{array}\right)\end{displaymath}$

(7.6)

Considering the convention according to which one suffix turning up twice in one term means adding up with respect to this suffix, (7.6) can be rewritten in the more compact form

$\begin{displaymath} P_i = d_{ij}\sigma_j \qquad \left(\begin{array} {c}i = 1, 2, 3\\ j = 1, 2, 3, 4, 5, 6\end{array}\right).\end{displaymath}$

(7.7)

It is important to notice that some authors do not introduce the multiplication factor two in the interpretation of the n = 4, 5 and 6 elements of the piezoelectric matrix. This, however, excludes the compact description of the relationship between the vector of the electric polarization and the mechanical stress presented in eq. (7.7).

Similarly other matrices representing various physical properties may be defined by different authors in different ways. Therefore when trying to use the numerical values as published in the literature the various definitions used by the authors should be taken into account.

Finally in order to demonstrate the advantage of the matrix notation let us investigate the elasticity of crystals. Hooke's law takes in tensor notation the following form

$\begin{displaymath} \sigma_{ij} = c_{ijkl}\varepsilon_{kl} \qquad (i, j, k, l = 1, 2, 3)\end{displaymath}$

(7.8)

where [ $\sigma_{ij}$ ] denotes the stress tensor and $\varepsilon_{kl}$ are the components of the deformation tensor.

Now, since the components of the [c_ijkl] tensor are symmetrical with regard to the first two and last two suffixes, respectively, these may be substituted each with one new suffix according to (7.3).

Further on the elements of the (c_mn) matrix can be defined by the equation

$\begin{displaymath} c_{ijkl} = c_{mn} \left(\begin{array} {c}i, j, k, l = 1, 2, 3\\ m, n = 1, 2, 3, 4, 5, 6\end{array}\right). \end{displaymath}$

(7.9)

Composing matrixes from the components of the [ $\sigma_{ij}$ ] stress according to (7.1), the components of the [ $\varepsilon_{kl}$ ] deformation tensor according to (7.2) and the components of the [c_ijkl] elasticity tensor according to (7.9) Hooke's law can be described with the following matrix equation

$\begin{displaymath} \left(\begin{array} {c} \sigma_1\\ \sigma_2\\ \sigma_3\\ \si... ...varepsilon_4 \\ \varepsilon_5\\ \varepsilon_6\end{array}\right)\end{displaymath}$

(7.10)

or, considering the convention of summation, in a more compact form.

$\begin{displaymath} \sigma_i = c_{ij}\varepsilon_j \qquad (i, j = 1, 2, 3, 4, 5, 6).\end{displaymath}$

(7.11)

Expressing the strains in terms of the stresses one obtains the equation

$\begin{displaymath} \varepsilon_i = s_{ij}\sigma_j \qquad (i, j = 1, 2, 3, 4, 5, 6) \end{displaymath}$

(7.12)

where (s_ij) is the reciprocal of the matrix (c_ij) and this leads to the equation

$\begin{displaymath} s_{ij}c_{jk} = c_{ij}s_{jk} = \delta{ik} \end{displaymath}$

(7.13)

$\delta{ik}$ denoting the Kronecker delta.

Simple calculation shows that between the elements of the above (s_mn) matrix and the components of the [s_ijkl] tensor expressing the relationship between the components of the [ $\varepsilon_{ij}$ ] strain and the [ $\sigma_{kl}$ ] stress respectively the following correspondence holds

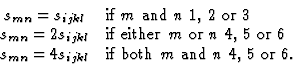$\begin{displaymath} \begin{array} {cl} s_{mn} = s_{ijkl} & \mbox{if } m \mbox{ a... ...\mbox{if both } m \mbox{ and } n \mbox{ 4, 5 or } 6.\end{array}\end{displaymath}$

(7.14)

Finally it should be noted that with the matrix notation, if applied, the number of the suffixes does not refer to the transformation formula of the matrix elements. Thus for example in case of a coordinate transformation the elements of the piezo-electric matrix (d_ij) transform differently from the matrix elements (c_ij) of the elasticity.

8. Curie's principle

The crystal symmetry depends upon the state of the crystal. If, due to some external influence, there is a change in the state of the crystal, there may also be a change in the crystal symmetry. The symmetry of a given state of a crystal may be determined using the Curie principle from the symmetry of the crystal free of any external influence and from the symmetry of the external influence.

According to Curie when various natural phenomena are piled upon each other forming a system, the dissymmetries are added up leaving only those elements which separately, in each phenomenon regarded in itself, were present. By dissymmetry Curie meant the sum of the absent symmetry elements.⁸ Curie's principle in itself may be formulated in the physics of crystals as follows: the symmetry group of a crystal under an external influence ( $\~{K}$ ) is given by the greatest common subgroup of the symmetry group of the crystal without the influence (K) and of the symmetry group of the external influence (G) considering also the mutual position of the symmetry elements of these groups:⁹

$\begin{displaymath} \~{K} = K \cap G \end{displaymath}$

(8.1)

Curie's principle expressed in other words: a crystal under an external influence will exhibit only those symmetry elements that are common to the crystal without the influence and the influence without the crystal.⁵

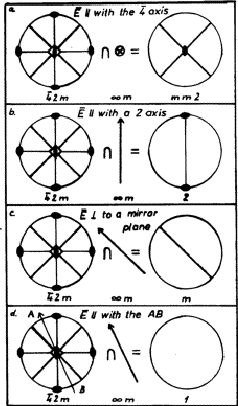
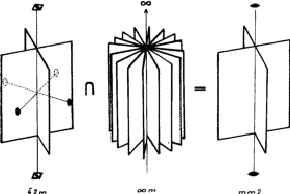
As an example let us investigate the change of symmetry in the ADP (ammonium dihydrogen phosphate) crystals in an electric field of various directions. The ground state symmetry of these crystals is $\=42m$ , i.e. it has a fourfold inversion axis (which contains in itself also a two-fold rotation axis). The fourfold inversion axis lies in the line of intersection of two mutually perpendicular planes of symmetry. Two diad axes are perpendicular to the fourfold inversion axis and at 45 $^{\circ}$ to the planes of symmetry. This is demonstrated in axionometric and stereographic representation respectively in Figs. 2 and 3. The symmetry of the electric field is $\infty {m}$ , i.e. it corresponds to the symmetry of a cone, which has an infinite-fold rotation axis containing every possible rotation axes of lower symmetry including also the twofold axes, further on the infinite-fold rotation axis lies in the line of intersection of an infinite number of mirror planes.

**Figure 2:** The decrease of the symmetry of an ADP crystal in an electric field of the [001] direction.
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

**Figure 3:** The change of the symmetry of an ADP crystal in electric fields of various directions.
$\begin{figure} \includegraphics {fig3.ps} \end{figure}$

First let us investigate the case when the electric field points in the [001] direction, which means that the vector of the electric field is parallel with the fourfold inversion axis of the crystal. The symmetry elements of the electric field do not include the inversion axis, therefore according to the Curie principle the resulting symmetry elements do not contain this axis. However, it should be observed that the fourfold inversion axis contains also a twofold rotation axis which is a symmetry element of the electric field, consequently the symmetry elements of the crystal in an electric field of the direction [001] will also contain this twofold axis. Of the basic symmetry elements the two mirror planes are also symmetry elements of the electric field, thus they are conserved in the crystal too. The twofold rotation axes perpendicular to the line of intersection of the mirror planes do not belong to the symmetry elements of the electric field, consequently they will disappear. Summing up the common symmetry elements of the electric field and the crystal in this field we have two mirror planes perpendicular to each other and a two-fold rotation axis in the line of intersection of the mirror planes. Thus the symmetry of the ADP crystal in the electric field of the [001] direction is reduced to the symmetry of the orthorhombic mm2 point group (Figs. 2 and 3a). If the electric field acts in the [ $\=100$ ] direction, i.e. along a twofold rotation axis perpendicular to the fourfold inversion axis no mirror plane of the crystal coincides with the mirror planes of the electric field which results in the disappearance of the mirror planes. Further on also the fourfold inversion axis (together with the twofold rotation axis connected with the inversion axis), and also from the two other twofold axes one axis will disappear, since the electric field has only in one direction a rotation symmetry. This way only the twofold rotation axis (along which the electric field is effective) remains conserved with the result that the symmetry of the crystal is reduced to the monoclinic point group 2 (as depicted in Fig. 3b). If the electric field influences the crystal in the [ $\=1\=10$ ] direction, i.e. in one mirror plane, the common symmetry element will be one mirror plane: the crystal symmetry is reduced to the point group m of the monoclinic system (Fig. 3c). Finally if the electric field points in an arbitrary [hkl] direction, different from the directions already discussed, no symmetry element of the crystal and the electric field coincides. Consequently no symmetry element is preserved. In this case the symmetry of the crystal is reduced to the trivial point group 1 of the triclinic system (Fig. 3d).

It follows from the foregoing that the originally optically uniaxial ADP crystal will under the influence of an electric field behave like an optically biaxial crystal.

It should be noted that the Curie principle constitutes only a special case of the great principle of the superposition of the symmetry groups. A detailed discussion of this subject, however, would go beyond the scope of this paper, one can refer to the book of Shubnikov and Koptsik.¹⁰

Acknowledgments

The author would like to thank Prof. M. P. Shaskolskaya, Dr. N. V. Perelomova and Dr. M. M. Tagieva for useful advice and valuable discussions. Further he thanks his colleagues for reading the manuscript and helpful comments.

References

1. Birss, R. R., Symmetry and Magnetism, Amsterdam, North-Holland Publishing Company (1964).

2. Bhagavantam, S., Crystal Symmetry and Physical Properties, London, New York, Academic Press (1966).

3. Sirotin, Yu. I. and Shaskolskaya, M. P., Fundamentals of Crystal Physics, Moscow, Mir Publishers (1982).

4. Fumi, F. G., Acta Cryst. 5 (1952) 44.

5. Nye, J. F., Physical Properties of Crystals, Oxford, Clarendon Press (1957).

6. Smith, A. C., Janak, J. F., Adler, R. B., Electronic Conduction in Solids, New York, McGraw-Hill Book Company (1967).

7. Hellwege, K. -H. (ed.), Landolt-Börnstein, New Series, Group III., Vol. 11, Berlin, Heidelberg, New York, Springer-Verlag (1979).

8. Curie, P., Oeuvres, pp. 118, Paris, Société Français de Physique (1908).

9. Koptsik, V. A., Sov. Phys. Cryst. 2 (1957) 99.

10. Shubnikov, A. V. and Koptsik, V. A., Symmetry in Science and Art, New York and London, Plenum Press (1977).

11. Shubnikov, A. V. and Belov, N. V., Colored Symmetry, Oxford, Pergamon Press (1964).

12. Juretschke, Hellmut, J., Crystal Physics, Massachusetts, W. A. Benjamin, Inc. Reading (1974).

13. Koptsik, V. A., Shubnikov's groups (In Russian), Moscow, Moscow University Press (1966).

14. Opechowski, W. and Guccione, R., Magnetic symmetry, G. T. Rado and H. Suhl (eds.), Magnetism, Vol. II/A, p. 105, New York, London, Academic Press (1965).

15. Shuvalov, L. A. (ed.), Modern Crystallography IV. Physical Properties of Crystals. Springer Series in Solid-State Sciences, Vol. 37. Springer- Verlag, in preparation.

16. Wooster, W. A., Tensors and Group Theory for the Physical Properties of Crystals, Oxford, Clarendon Press (1973).

17. Perelomova, N. V. and Tagieva, N. M., Problems in Crystal Physics with solutions, Moscow, Mir Publishers (1983).

Many further references are found in each of the cited books.

Crystallography Matters!