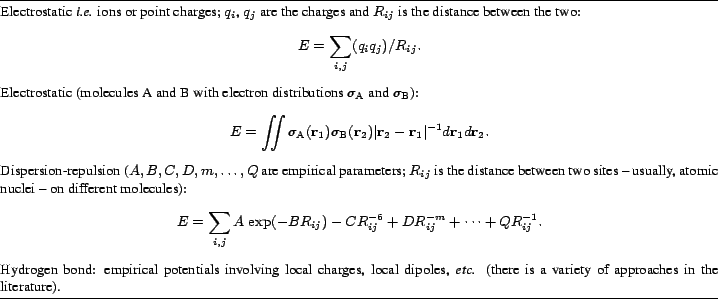Crystal packing
Angelo Gavezzotti and Howard Flack
Introduction
We all know by everyday experience that matter has many different states of aggregation. Chemists also know that matter is made of atoms, ions and molecules, and that the macroscopic properties of any object depend on the size, shape and energies of these microscopic constituents.
One mole of gaseous substance occupies about 24 litres at room temperature, while the volume of the same amount of substance in the liquid or solid state is a few tens to a few hundred millilitres. It follows that the molecules![]() 1 are much, much closer to each other in a liquid and a solid than in a gas. An easy calculation shows that in condensed phases the average volume per molecule is about one and a half times the volume of the molecule itself. Molecules are tightly packed in space, and therefore the compressibility of condensed media is very small. You can sit on a rock simply because its atoms and molecules are so close to each other that they cannot give way under external pressure.
1 are much, much closer to each other in a liquid and a solid than in a gas. An easy calculation shows that in condensed phases the average volume per molecule is about one and a half times the volume of the molecule itself. Molecules are tightly packed in space, and therefore the compressibility of condensed media is very small. You can sit on a rock simply because its atoms and molecules are so close to each other that they cannot give way under external pressure.
A gas will diffuse very quickly out of an open bottle, while a solid can usually be left in the open air almost indefinitely without apparent change in size and shape (there are exceptions, like mothballs). Besides repelling each other at short distances, molecules in a solid are reluctant to leave their neighbours; this means that some sort of attraction is holding them together. Temperature has a much more dramatic effect on all this than pressure: ordinary liquids boil when heated mildly, and even solid rock melts and vaporizes in volcanic depths.
Through simple reasoning on elementary evidence, we are led to the following conclusions: upon cooling or with increasing pressure, molecules stick together and form liquid and solid bodies, in which the distance between them is of the same order of magnitude as the molecular dimensions; and an increasing repulsion arises if they are forced into closer contact. The reverse occurs upon heating or lowering the external pressure.
While a layman may be more than satisfied at this point, a scientist must ask him- or herself at least two further questions: (1) What is the nature and magnitude of the forces holding molecules together? (2) What is the geometrical arrangement of molecules at close contact? Restricting the scope, as we do in this pamphlet, to crystalline solids, these questions define the subject of crystal packing. Since crystals are endowed with the beautiful gift of order and symmetry, the spatial part (2) is not trivial. Packing forces and crystal symmetry determine the chemical and physical properties of crystalline materials.
Thermodynamics and kinetics
Now put yourself in the place of a molecule within a pure and perfect crystal, being heated by an external source. At some sharply defined temperature, a bell rings, you must leave your neighbours, and the complicated architecture of the crystal collapses to that of a liquid. Textbook thermodynamics says that melting occurs because the entropy gain in your system by spatial randomization of the molecules has overcome the enthalpy loss due to breaking the crystal packing forces:
This rule suffers no exceptions when the temperature is rising. By the same token, on cooling the melt, at the very same temperature the bell should ring again, and molecules should click back into the very same crystalline form. The entropy decrease due to the ordering of molecules within the system is overcompensated by the thermal randomization of the surroundings, due to the release of the heat of fusion; the entropy of the universe increases.
But liquids that behave in this way on cooling are the exception rather than the rule; in spite of the second principle of thermodynamics, crystallization usually occurs at lower temperatures (supercooling). This can only mean that a crystal is more easily destroyed than it is formed. Similarly, it is usually much easier to dissolve a perfect crystal in a solvent than to grow again a good crystal from the resulting solution. The nucleation and growth of a crystal are under kinetic, rather than thermodynamic, control.
Forces
A molecule consists of a collection of positively charged atomic nuclei surrounded by an electron cloud. Even if the molecule has no net charge, such an object can hardly be considered as electrically neutral. Its electrostatic potential is a superposition of the fields of all nuclei and electrons. An approaching charge can alter, by its own electrostatic field, the electron distribution in a molecule; this phenomenon is called polarization.
The attractive forces holding molecules together are a consequence of molecular electrostatic potentials. For purely ionic crystals, one can just use Coulomb's law with integer charges; for organic molecules, it takes a more complicated expression, involving an integration over continuous electron densities. Alternatively, the charge distribution can be represented by a series expansion using multipoles, and the interaction energy can be calculated as a function of multipole moments.
Different atoms have different electronegativities. Larger charge separations within the molecule - in the jargon of the trade, more polar molecules - build up stronger intermolecular forces. Ionic crystals are very hard and stable, while naphthalene or camphor (two common ingredients of mothballs) sublime rather easily. These non-polar hydrocarbon molecules must rely on mutual polarization to produce attraction; the resulting forces are feeble, and are called dispersion or van der Waals' forces; they are usually described by empirical formulae. In this way, even argon manages to form a solid at very low temperature.
Ubiquitous in crystals is the hydrogen bond, a polar interaction which is the most effective means of recognition and attraction between molecules; so effective, that molecules with donor and acceptor groups form hydrogen bonds without exception. There is no case (at least, to the authors' knowledge) where a molecule that can form hydrogen bonds does not do so in the crystal.
The repulsion at short intermolecular distance arises from a quantum mechanical effect. According to Pauli's principle, electrons with the same quantum numbers, no matter if belonging to different molecules, cannot occupy the same region of space. Thus, Pauli "forces" - although they are not forces in the sense of Newtonian mechanics - steer electrons to mutual avoidance, and the total energy of the electron system rises if paired electrons are pulled together.
Table 1 collects the simple potentials mentioned so far. Direct but non-specific measures of the strength of crystal forces are the melting temperature and the sublimation enthalpy.
Crystal symmetry
Intermolecular attraction brings molecules together, but there is a priori no implication of order and symmetry. Glasses, in which molecules are oriented at random, are sometimes as stable as crystals, in which molecules are arranged in an ordered fashion. The ordering of irregularly shaped, electrically charged molecules does however imply anisotropy; for mechanical properties, it results in preferential cleavage planes, while the consequences of optical, electrical and magnetic anisotropy lead to a variety of technological applications of crystalline materials. But what is the link between order, symmetry and crystal stability?
Crystal symmetry![]() 2 has two facets. On one side, in a milestone mathematical development, it was demonstrated that the possible arrangements of symmetry operations (inversion through a point, rotation, mirror reflection, translation, etc.) give rise to no less and no more than 230 independent three-dimensional space groups. After the advent of X-ray crystallography, space-group symmetry was determined from the systematic absences in diffraction patterns and used to help in the calculation of structure factors and electron-density syntheses.
2 has two facets. On one side, in a milestone mathematical development, it was demonstrated that the possible arrangements of symmetry operations (inversion through a point, rotation, mirror reflection, translation, etc.) give rise to no less and no more than 230 independent three-dimensional space groups. After the advent of X-ray crystallography, space-group symmetry was determined from the systematic absences in diffraction patterns and used to help in the calculation of structure factors and electron-density syntheses.
The other side of crystal symmetry has to do with the crystal structure, as resulting from mutual recognition of molecules to form a stable solid. This is a fascinating and essentially chemical subject, which requires an evaluation and a comparison of the attractive forces at work in the crystal. Space-group symmetry is needed here to construct a geometrical model of the crystal packing, and it comes into play in judging relative stabilities.
It should be clear that the necessary arrangements of symmetry operations in space bear no immediate relationship to crystal chemistry. The fact that 230 space groups exist does not mean that molecules can freely choose among them when packing in a crystal. Far from it, there are rather strict packing conditions that must be met, and this can be accomplished only by a limited number of arrangements of very few symmetry operations; for organic compounds, these are inversion through a point ( ![]() ), the twofold screw rotation (2) and the glide reflection (
), the twofold screw rotation (2) and the glide reflection (![]() ). Some space groups are mathematically legitimate, but chemically impossible, and the crystal structures of organic compounds so far determined belong to a rather restricted number of space groups[1,2,3] (Table 2).
). Some space groups are mathematically legitimate, but chemically impossible, and the crystal structures of organic compounds so far determined belong to a rather restricted number of space groups[1,2,3] (Table 2).
| Rank | Group | No. of crystals | Molecules in general position | Point-group symmetry |
| 1 | 9056 | 8032 (89%) | ||
| 2 | 4415 | 4415 (100%) | 1 | |
| 3 | 3285 | 2779 (85%) | ||
| 4 | 2477 | 2477 (100%) | 1 | |
| 5 | 1371 | 802 (58%) | ||
| 6 | 1180 | 1064 (90%) | ||
| 7 | 445 | 445 (100%) | 1 | |
| 8 | 370 | 370 (100%) | 1 | |
| 9 | 275 | 225 (82%) | 2 | |
| 10 | 266 | 33 (12%) | ||
| 12 | 205 | 94 (46%) | ||
| 14 | 127 | 40 (31%) | ||
| 16 | 92 | 46 (50%) | 2 | |
| 17 | 88 | 51 (58%) | 2 |
When charge is evenly distributed in a molecule, and there is no possibility of forming hydrogen bonds, no special anchoring points exist. Every region of the molecule has nearly the same potential for intermolecular attraction, and hence it is reasonable to expect that each molecule be surrounded by as many neighbours as possible, forming as many contacts as possible. Empty space is a waste, and molecules will try to interlock and to find good space-filling arrangements. This close-packing idea appeared very early in its primitive form[4], but was consciously put forward by Kitaigorodski[5].
Order and symmetry now come to the fore, since for an array of identical objects a periodic, ordered and symmetrical structure is a necessary (although not sufficient) condition for an efficient close packing. When special interactions (like hydrogen bonds) are present, the close-packing requirement may be a little less stringent (Figure 1), but it turns out that all stable crystals have a packing coefficient![]() 3 between 0.65 and 0.80.
3 between 0.65 and 0.80.
![\includegraphics[width=8cm]{fig1.eps}](https://www.iucr.org/__data/assets/image/0010/14887/img37.png) |
Symmetry operations
In a crystal, some symmetry operations can be classified as intramolecular, meaning that they relate different parts of the same molecule and thus belong to the molecular point-group symmetry. The other symmetry operations, which act as true crystal-packing operators, may be called intermolecular, and these are the ones which relate different molecules in the crystal. This classification implies that molecules be distinguishable in crystals.
The simplest intuitive way of viewing a symmetry operation is that it reproduces in space one, or more if applied repetitively, congruent or enantiomorphic copies of a given object, according to a well-defined convention (Figure 2). The spatial relationship between the parent and the reproduced molecules is strict, so a moment's pondering will convince the reader that some operators are more effective than others towards close packing. For objects of irregular shape, mirror reflection and twofold rotation produce bump-to-bump confrontation, while inversion through a point, screw rotation and glide reflection favour bump-to-hollow, more close-packed arrangements (Figure 3). One must not forget that pure translation (![]() ) is always present in a crystal. Except when infinite strings or layers are present, it is an intrinsically intermolecular operator, whose role in close-packing is probably intermediate (Figure 4); space group
) is always present in a crystal. Except when infinite strings or layers are present, it is an intrinsically intermolecular operator, whose role in close-packing is probably intermediate (Figure 4); space group ![]() is the eighth most populated one for organic substances.
is the eighth most populated one for organic substances.
![\includegraphics[width=10cm]{fig2.eps}](https://www.iucr.org/__data/assets/image/0003/14889/img39.png) |
![\includegraphics[width=8cm]{fig3.eps}](https://www.iucr.org/__data/assets/image/0006/14892/img41.png) |
![\includegraphics[width=12cm]{fig4.eps}](https://www.iucr.org/__data/assets/image/0007/14893/img42.png) |
The clearest proof of the leading role of ![]() ,
, ![]() and
and ![]() in close packing comes from a statistical analysis of the space-group frequencies of organic compounds, care being taken to distinguish between inter- and intramolecular symmetry operations. Table 2 shows that mirror reflection and twofold rotation appear in organic crystals most often as intramolecular operators: thus
in close packing comes from a statistical analysis of the space-group frequencies of organic compounds, care being taken to distinguish between inter- and intramolecular symmetry operations. Table 2 shows that mirror reflection and twofold rotation appear in organic crystals most often as intramolecular operators: thus ![]() is a favourite for molecules with twofold axes,
is a favourite for molecules with twofold axes, ![]() for molecules with mirror symmetry, and for these space groups the percentage of structures with molecules in general positions is very low.
for molecules with mirror symmetry, and for these space groups the percentage of structures with molecules in general positions is very low. ![]() is an apparent exception; in fact, the combination of the centring translation and a twofold rotation results in a twofold screw rotation. Viewing the issue from the other end, Table 3 shows that pairwise combinations of
is an apparent exception; in fact, the combination of the centring translation and a twofold rotation results in a twofold screw rotation. Viewing the issue from the other end, Table 3 shows that pairwise combinations of ![]() ,
, ![]() and
and ![]() produce rows, layers or full structures in all the most populated space groups for organics. A student who cares to work out in detail the results in this Table will understand all the basic principles of geometrical crystallography and crystal symmetry.
produce rows, layers or full structures in all the most populated space groups for organics. A student who cares to work out in detail the results in this Table will understand all the basic principles of geometrical crystallography and crystal symmetry.
2, twofold rotation; ![]() , mirror reflection;
, mirror reflection; ![]() , glide reflection;
, glide reflection; ![]() , twofold screw rotation;
, twofold screw rotation; ![]() , inversion through a point;
, inversion through a point; ![]() , centring translation. The superscript upper-case labels preceding each space-group symbol are as follows: C cluster, R row, LL layer and 3D full three-dimensional structure. When several possibilities are given for an arrangement, they depend on the relative orientation of the symmetry operations. As the full matrix of these pairs of symmetry operations is symmetric, only the lower triangle is given.
, centring translation. The superscript upper-case labels preceding each space-group symbol are as follows: C cluster, R row, LL layer and 3D full three-dimensional structure. When several possibilities are given for an arrangement, they depend on the relative orientation of the symmetry operations. As the full matrix of these pairs of symmetry operations is symmetric, only the lower triangle is given.
| 2 | ||||||||
A similar statistic, taking account of the local symmetry of the constituent units, is not available for inorganic compounds, but a similar trend would probably be found. These compounds frequently contain highly symmetrical (tetrahedral, triangular, square-planar) ions or groups, which carry over their symmetry to the crystal. This causes a spread of the space-group frequencies towards the tetragonal, hexagonal or cubic systems (a no-man's land for organics); no space group has more than 10% of the structures for inorganic compounds (Table 4).
One can never be careful enough when generalizing on such topics; crystal packing is a subtle, elusive subject. To give just an example of its intricacies, when dealing with the importance of symmetry to crystal packing one should consider that a symmetry operation is relevant only when it relates close-neighbour molecules. Wilson[8,9] has pointed out that, in some space groups, some symmetry elements![]() 4 may be silent, or "encumbered"; they are prevented, by their location in space, from acting between first-neighbour molecules. The relative importance of symmetry operators in the most populated space groups has been quantified by packing-energy calculations[11].
4 may be silent, or "encumbered"; they are prevented, by their location in space, from acting between first-neighbour molecules. The relative importance of symmetry operators in the most populated space groups has been quantified by packing-energy calculations[11].
Another reminder: the choice of a space group is to some extent arbitrary; for example one might argue that in some cases the presence or absence of a centre of symmetry is a questionable matter. This may be true for all symmetry operations; a glide reflection can be almost operative, and its assignment can be a matter of sensitivity of the apparatus for the detection of weak reflections, in particular the borderline between a "very weak" and a "systematically absent" reflection can even be a matter of personal taste. In this respect, the sensitivity of single-crystal X-ray diffraction experiments to minor deviations is very high, and the presence of a semi- or pseudo-symmetry operation, violated because of minor molecular details, has the same chemical meaning as that of a fully-observed symmetry operation.
What to say, then, of crystals with more than one molecule in the asymmetric unit, ![]() ? Many are presumably just cases of the accidental overlooking of some symmetry in the crystal-structure determination and refinement, and many more do have pseudo-symmetry operations relating the molecules in the asymmetric unit (see the remarks in the previous paragraph). The conformations of the independent molecules are usually quite similar[12]. While the overall frequency of structures with
? Many are presumably just cases of the accidental overlooking of some symmetry in the crystal-structure determination and refinement, and many more do have pseudo-symmetry operations relating the molecules in the asymmetric unit (see the remarks in the previous paragraph). The conformations of the independent molecules are usually quite similar[12]. While the overall frequency of structures with ![]() is about 8% for organics[13], they seem to be unevenly distributed among chemical classes. For example, for monofunctional alcohols the frequency rises to 50%; a possible interpretation is in terms of hydrogen-bonded dimers and oligomers which are already present in the liquid state, and are so strongly bound that they are transferred intact to the crystal.
is about 8% for organics[13], they seem to be unevenly distributed among chemical classes. For example, for monofunctional alcohols the frequency rises to 50%; a possible interpretation is in terms of hydrogen-bonded dimers and oligomers which are already present in the liquid state, and are so strongly bound that they are transferred intact to the crystal.
The case is similar for molecules which must pick up solvent molecules to crystallize in the form of solvates, or which can form inclusion compounds with a variety of guest molecules. The reasons for the appearance of these phenomena, and their control, are presently beyond reach but see [14].
Crystal-structure descriptors
Simple but useful crystal-structure descriptors are the density, the melting point and the packing coefficient; mention of the first is mandatory for papers in Acta Crystallographica, but unfortunately mention of the other two is not.
The intermolecular geometry is another Cinderella in crystallographic papers. Clearly, a long list of intermolecular interatomic distances is generally not useful or significant but, for hydrogen-bonded crystals, the crucial X![]() X or H
X or H![]() X contact distances are usually sufficient. As a general rule, the description of intermolecular geometry requires the use of macro-coordinates, like the distances between molecular centres of mass or the angles between mean molecular planes in different molecules or fragments. It can be said that the crystal structure of naphthalene can be described by just two parameters - the angle between the molecular planes of glide-related molecules and the distance between their centres of mass - which contain most if not all of the chemical information on the properties of the crystalline material. It is also unfortunate that such macrogeometry is very seldom highlighted in crystallographic papers, and has to be painstakingly recalculated from the atomic coordinates.
X contact distances are usually sufficient. As a general rule, the description of intermolecular geometry requires the use of macro-coordinates, like the distances between molecular centres of mass or the angles between mean molecular planes in different molecules or fragments. It can be said that the crystal structure of naphthalene can be described by just two parameters - the angle between the molecular planes of glide-related molecules and the distance between their centres of mass - which contain most if not all of the chemical information on the properties of the crystalline material. It is also unfortunate that such macrogeometry is very seldom highlighted in crystallographic papers, and has to be painstakingly recalculated from the atomic coordinates.
A crystal model suitable for computer use can be built very simply, using the crystal coordinates for a reference molecule (RM) and the space-group matrices and vectors, as given in International Tables for Crystallography Vol. A[10]. In this respect, finding in the primary literature a set of atomic coordinates representing a completely-connected molecular unit, as near as possible to the origin of the crystallographic reference system, with a reduced cell and in a standard space group, ![]() the number of molecules in the asymmetric unit and an indication of the molecular symmetries, helps in saving a substantial amount of time and mistakes (let this be said as an encouragement to experimental X-ray crystallographers to help their theoretician colleagues). The required algebra is as follows. Calling
the number of molecules in the asymmetric unit and an indication of the molecular symmetries, helps in saving a substantial amount of time and mistakes (let this be said as an encouragement to experimental X-ray crystallographers to help their theoretician colleagues). The required algebra is as follows. Calling ![]() the original atomic fractional coordinates of the RM,
the original atomic fractional coordinates of the RM, ![]() and
and ![]() a space-group matrix and (column) translation vector, the atomic coordinates in a given surrounding molecule (SM) are given by:
a space-group matrix and (column) translation vector, the atomic coordinates in a given surrounding molecule (SM) are given by:
From this expression the coordinates of all atoms in the crystal model can be calculated, remembering that translation vectors whose components are an arbitrary combination of integer unit cell translations can always be added to the ![]() vectors.
vectors.
A most important crystal property that can be calculated by this model is the packing energy. For an ionic crystal, if the coordinates and charges of all ions in the crystal model are known, the interionic distances and hence the Coulombic energy can be calculated. In organic crystals with dispersive--repulsive forces, the packing energy can be approximated by empirical formulae:
where ![]() is an intermolecular interatomic distance, and
is an intermolecular interatomic distance, and ![]() ,
, ![]() and
and ![]() are empirical parameters.
are empirical parameters.
Chirality
A chiral object is one which cannot be superposed on its mirror image. The symmetry group of a chiral object contains only pure rotations, pure translations, and screw rotations. All of these operations correspond to movements which may be carried out on a rigid body. In nature, chiral objects occur as both mirror-related versions and these are called enantiomorphs. For a chiral molecule the special term enantiomer has been coined. On the other hand, an achiral object can be superposed on its mirror image and its symmetry group must contain some operations which invert its geometry, viz pure rotoinversion operations (![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ) or glide reflection. None of these operations can be produced by a direct movement of a rigid body.
) or glide reflection. None of these operations can be produced by a direct movement of a rigid body.
Chirality plays a mischievous role in the packing together of molecules to form crystals. It is easy to build a spiral staircase (really it is helicoidal) from bricks. The staircase is chiral and the bricks are achiral. Are there any restrictions due to symmetry or geometry in the way that chiral or achiral molecules may be put together to form a chiral or an achiral crystal structure? In answering this question for chiral molecules we have two common cases in mind: (i) all of the enantiomers have the same chirality - the composition of the sample is said to be enantiopure or enantiomerically pure; (ii) exactly one half of the enantiomers are of one chirality and the other half of the opposite - the sample is a racemate. Of the six combinations achiral/enantiopure/racemate forming achiral/chiral crystal structures, all but one have been observed experimentally and another one is very rare. No example has been observed of a well-ordered achiral crystal structure formed of enantiopure chiral molecules. Although it may seem obvious that an enantiopure compound must form a chiral crystal structure, in fact this behaviour is due to the individuality of the molecules rather than to any underlying theorem of symmetry groups. The very rare case is the one in which a racemate forms a chiral crystal structure. At first sight this sounds counterintuitive but there is no obligation for the enantiomers either to be related one to another by a rotoinversion or a glide reflection belonging to the space group of the crystal structure or to have the same configuration in the solid state.
Crystallization of a racemate from solution or the melt frequently results in the formation of crystals with a homogeneous crystal structure containing both enantiomers in equal proportion. In the old literature this is known as a "racemic compound". However, occasionally crystallization of a racemate produces a racemic conglomerate in which the composition of each crystal is enantiopure, there being equal numbers of left-handed and right-handed crystals. In this case, a spontaneous resolution has been achieved, and this phenomenon is often quoted as one of the possible sources of enantiopurity in the biological world. The reasons for such a selectivity, undoubtedly brought about by crystal-packing requirements, is part of the mystery that shrouds the formation of crystalline solids. A comparison between the crystal structures of enantiopure compounds and their racemates shows that frequently both are formed of the same enantiopure rods or layers. The latter are packed together differently in the crystal structures of the enantiopure compounds and the racemates. A comparative study of the crystal packing of enantiopure compounds and of their racemates has been carried out[15]; no clear sign of a more compact crystal packing has been found for racemates.
Many natural products whose crystal structures appear in the Cambridge Structural Database have been isolated in enantiomerically-pure form from plants or animals. Natural compounds are chemically and biologically interesting so their crystal structures are determined more frequently than synthetic products. Thus the frequency of occurrence in the CSD of chiral crystal structures and of the 65 space groups containing only symmetry operations of the first kind (translations, pure and screw rotations) is artificially increased.
The free energies of a pair of enantiomers are identical. Nevertheless kinetic effects in the crystallization of racemates, or more generally enantiomeric mixtures, are rife and in some cases are used industrially to undertake the resolution of racemates. The key to the matter is supersaturation and the seeding of the crystallization solution. Although the effect was first mentioned in a very succinct letter to Louis Pasteur by one of his PhD students, we prefer to give a brief account of Alfred Werner's rediscovery and use of the phenomenon. Werner had synthesised a chiral complex of cobalt which did not racemize in solution. His initial product contained about 60% of the D enantiomer and 40% of the L. Taking this product into concentrated supersaturated solution, lowering the temperature and halting the crystallization at the appropriate moment, he obtained crystals of the enantiopure D. The real surprise was the composition of the remaining product in solution. This turned out to be 40% D and 60% L, the exact opposite of the starting solution. Werner had only to filter off his pure D, concentrate the remaining solution and recommence the crystallization. The second crop of crystals was, of course, the enantiopure L compound.
It is difficult, if not impossible, to ascertain the frequency of spontaneous resolution by crystallization to give a racemic conglomerate, because the chemical history of the sample and the enantiopurity of the starting materials for crystal formation and growth are seldom or never mentioned by the authors of crystallographic papers. A source of potentially extremely useful chemical information is thus lost. It is most useful to characterise both the bulk compound and the single crystal used for the diffraction studies by measurement of the optical activity, circular dichroism or enantioselective chromatography.
Polymorphism
It was said earlier in this pamphlet that crystal nucleation and growth are quite often under kinetic control. The final product, the (single) crystal, may result from less stable but faster growing nuclei; the transformation to the thermodynamically stable phase is hindered by an energy barrier, because the forces holding the metastable phase together have to be overcome, so that molecules can rearrange into the stable crystalline form. In some favourable (and almost exceptional) cases, the spatial rearrangement is so simple that a highly cooperative single-crystal to single-crystal transformation can occur.
The natural outcome of all this is polymorphism, or the ability of a given compound to crystallize in different crystal structures. Thermodynamics holds that only one structure is the stable one at a given temperature and pressure but, not surprisingly, kinetics sometimes allows many coexisting phases[16]. A typical enthalpy difference between polymorphs for an organic compound is 4-8 kJ/mole, which, for transition temperatures of the order of 300 K, implies entropy differences of the order of 10-20 J K-1 mole-1 (![]() G = 0 =
G = 0 = ![]() H-T
H-T![]() S). These figures are now at the borderline of the accuracy of both detection apparatus and theoretical methods[17,18].
S). These figures are now at the borderline of the accuracy of both detection apparatus and theoretical methods[17,18].
A further influence on crystal growth in terms of shape and structure is that of the presence of impurities. Crystal morphology is affected by the adsorption of impurity molecules on to particular faces of the crystal with a consequent slowing in their growth rate. Impurities trapped in the host crystal, especially those that are close in chemical structure to the bulk compound, may cause it to adopt a different structure. A few cases are known of opposite enantiomers adopting different structures although grown under similar conditions.
Experiments
X-ray and neutron diffraction give a detailed picture of crystal packing. It is difficult to find, in all natural sciences, a more undisputable experimental result, than that of well-performed single-crystal diffraction work. The information is however mainly static, although skillful elaborations may provide a tinge of dynamics to the picture.
Crystal dynamics may be probed by infra-red spectroscopy, for the frequencies of lattice vibrations. Hole-burning spectroscopy can address single impurity molecules in a crystalline environment, and so potentially probe the packing environment. NMR spectroscopy can be used to detect molecular motions and large-amplitude rearrangements, ESR spectroscopy to study the fate of organic radicals produced after a chemical reaction in a crystal.
All measurements of mechanical, electrical, optical, or magnetic properties of crystals are in principle relevant to the study of molecular packing. These experiments are seldom performed by chemists, being beyond the border with the realm of solid-state physics. The relationship between these properties and the crystal structure is strict, but not known in a systematic way.
One most important experiment for the science of crystal packing is a humble one, that is performed every day in every chemical laboratory, but whose results are seldom recorded and almost never published: crystallization from solution. This is a small step for any single chemist, but a systematic analysis of the relationship between molecular structure and ease of crystallization from many solvents and in many temperature conditions would be a giant leap for the chemical sciences.
Concluding remarks, and a suggestion
Crystal packing is a fascinating, and at the same time such a complicated phenomenon. The physics of the interaction between molecules is relatively simple, but the rules that determine the ways in which these forces can be satisfied are complex and still obscure. For this reason, crystal packing prediction and control are still far-away goals: there are simply too many spatial possibilities with very nearly the same free energy.
The principles of crystal packing are still largely unknown. No one has a unique and general answer even to the most fundamental question: Why do some substances crystallize readily at ordinary conditions, and others do not? Is there any trend in molecular size, shape, stoichiometry, conformation, polarity, that accounts for the ability to crystallize? And then, more detail; for example, for nonlinear-optics applications, it is important to grow non-centrosymmetric crystals, but no one knows why and when a molecule will adopt an inversion centre in forming its crystal structure.
The problem is being tackled, however. On one side, we have the Cambridge Structural Database (CSD), with an enormous potential for intermolecular information, which can be studied by statistics. On the other side, a number of theoretical techniques can be used; for example, if a reliable intermolecular potential function is available, the packing energies of different crystal structures for the same compound can be calculated and compared[19]; eventually, a full molecular dynamics simulation may become possible.
In our times, scientific breakthroughs are fostered by large numbers of small, most often unconscious, contributions. The accumulation of basic data plays a key role. But the problem is to look at the right things.
The age of intramolecular structural chemistry is declining for small molecules. There is very little that can be added to the average intramolecular geometrical data collected![]() by use of the Cambridge Structural Database; anything at variance with these well-established averages is most probably wrong. Long experience has shown that discussing electronic effects in terms of molecular geometry alone is a tricky business. So, if you are an X-ray diffractionist, instead of looking at your molecule, try looking at your crystal. There is plenty to be discovered, at a low cost and with perfectly high confidence, by looking at what molecules do when they interact with each other, and single-crystal X-ray diffraction is still the best technique for this purpose.
by use of the Cambridge Structural Database; anything at variance with these well-established averages is most probably wrong. Long experience has shown that discussing electronic effects in terms of molecular geometry alone is a tricky business. So, if you are an X-ray diffractionist, instead of looking at your molecule, try looking at your crystal. There is plenty to be discovered, at a low cost and with perfectly high confidence, by looking at what molecules do when they interact with each other, and single-crystal X-ray diffraction is still the best technique for this purpose.
References
1. R. P. Scaringe (1991). A Theoretical Technique for Layer Structure Prediction, in Electron Crystallography of Organic Molecules, edited by J. R. Fryer and D. L. Dorset, pp 85-113. Dordrecht: Kluwer Academic Publishers.
2. W. H. Baur and D. Kassner (1992). The perils of Cc: comparing the frequencies of falsely assigned space groups with their general population. Acta Cryst. B48, 356-369 [doi:10.1107/S0108768191014726].
3. C. P. Brock and J. D. Dunitz (1994). Towards a grammar of crystal packing. Chem. Mater. 6, 1118-1127 [doi:10.1021/cm00044a010].
4. W. Barlow and W. J. Pope (1906). A development of the atomic theory which correlates chemical and crystalline structure and leads to a demonstration of the nature of valency. J. Chem. Soc. 89, 1675-1744.
5. A. I. Kitaigorodski (1961). Organic Chemical Crystallography. New York: Consultants Bureau.
6. A. Gavezzotti (1976). Atti Accad. Naz. Lincei, Ser. VIII, Vol. XIII, pp 107-119; plane group figures are available at the site http://www.iucr.org/iucr-top/comm/cteach/pamphlets/21/sup/.
7. A. Gavezzotti (1983). The calculation of molecular volumes and the use of volume analysis in the investigation of structured media and of solid-state organic reactivity. J. Am. Chem. Soc. 105, 5220-5225 [doi:10.1021/ja00354a007].
8. A. J. C. Wilson (1988). Space groups rare for organic structures. I. Triclinic, monoclinic and orthorhombic crystal classes. Acta Cryst. A44, 715-724 [doi:10.1107/S0108767388004933].
9. A. J. C. Wilson (1990). Space groups rare for organic structures. II. Analysis by arithmetic crystal class. Acta Cryst. A46, 742-754 [doi:10.1107/S0108767390004901].
10. International Tables for Crystallography. (2002). Vol. A, Space-group symmetry, edited by Th. Hahn, 5th ed. Dordrecht: Kluwer Academic Publishers.
11. G. Filippini and A. Gavezzotti (1992). A quantitative analysis of the relative importance of symmetry operators in organic molecular crystals. Acta Cryst. B48, 230-234 [doi:10.1107/S0108768191011977].
12. N. Gautham (1992). A conformational comparison of crystallographically independent molecules in organic crystals with achiral space groups. Acta Cryst. B48, 337-338 [doi:10.1107/S0108768191013307].
13. N. Padmaja, S. Ramakumar and M. A. Viswamitra (1990). Space-group frequencies of proteins and of organic compounds with more than one formula unit in the asymmetric unit. Acta Cryst. A46, 725-730 [doi:10.1107/S0108767390004512].
14. L. R. Nassimbeni (2003). Physicochemical aspects of host-guest compounds. Acc. Chem. Res. 36, 631-637 [doi:10.1021/ar0201153].
15. C. P. Brock, W. B. Schweizer and J. D. Dunitz (1991). On the validity of Wallach's rule: on the density and stability of racemic crystals compared with their chiral counterparts. J. Am. Chem. Soc. 113, 9811-9820 [doi:10.1021/ja00026a015].
16. J. A. R. P. Sarma and J. D. Dunitz (1990). Structures of three crystalline phases of p-(trimethylammonio)benzenesulfonate and their interconversions. Acta Cryst. B46, 784-794 [doi:10.1107/S0108768190007480].
17. A. Gavezzotti (1994). Are crystal structures predictable? Acc. Chem. Res. 27, 309-314 [doi:10.1021/ar00046a004].
18. A. Gavezzotti and G. Filippini (1995). Polymorphic forms of organic crystals at room conditions: thermodynamic and structural implications. J. Am. Chem. Soc. 117, 12299-12305 [doi:10.1021/ja00154a032].
19. A. Gavezzotti (1996). Polymorphism of 7-dimethlaminocyclopenta[c]coumarin: packing analysis and generation of trial crystal structures. Acta Cryst. B52, 201-208 [doi:10.1107/S0108768195008895].
20. F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen and R. Taylor (1987). Tables of bond lengths determined by X-ray and neutron diffraction. Part 1. Bond lengths in organic compounds. J. Chem. Soc. Perkin II, S1-S19 [doi:10.1039/P298700000S1].
Suggestions for further reading
(a) Two fundamental books on condensed phases are those by A. Bondi, Physical Properties of Molecular Crystals, Liquids and Glasses, New York: Wiley (1968), and A. R. Ubbelohde, The Molten State of Matter: melting and crystal structure, Chichester: Wiley (1978). They are long out of print, but may be still available in your chemistry library.
(b) The works of A. I. Kitaigorodski, a pioneer in the field of crystal packing studies, are collected in two main books: (i) the one quoted in [5]; (ii) A. I. Kitaigorodski, Molecular Crystals and Molecules, New York: Academic Press (1973).
(c) A similar role is played for inorganic structures by the multi-author book: Structure and Bonding in Crystals, edited by M. O'Keeffe and A. Navrotsky, New York: Academic Press (1981).
(d) A compendium of the theory of the structure and of the optical and electrical properties of organic materials is in J. D. Wright, Molecular Crystals, Cambridge University Press (1987).
(e) If you want to read an amusing and stimulating book, and learn about molecular orbitals for periodic systems into the bargain: R. Hoffmann, Solids and Surfaces, a Chemist's View of Bonding in Extended Structures, New York: VCH (1988).
(f) On methods for the investigation of the geometrical and energetic properties of crystal packing, see: Crystal symmetry and molecular recognition in Theoretical aspects and computer modeling of the molecular solid state, edited by A. Gavezzotti, Chichester: Wiley and Sons (1997); A. Gavezzotti and G. Filippini (1998), Self-organization of small organic molecules in liquids, solutions and crystals: static and dynamic calculations, Chem. Commun. 3, 287-294 [doi:10.1039/a707818h]; A. Gavezzotti (1998), The crystal packing of organic molecules: challenge and fascination below 1000 dalton, Crystallogr. Rev. 7, 5-121; J. D. Dunitz and A. Gavezzotti (1999), Attractions and repulsions in organic crystals: what can be learned from the crystal structures of condensed-ring aromatic hydrocarbons? Acc. Chem. Res. 32, 677-684 [doi:10.1021/ar980007+]; A. Gavezzotti (2002), The chemistry of intermolecular bonding: organic crystals, their structures and transformations, Synth. Lett., pp. 201-214; A. Gavezzotti (2002), Structure and intermolecular potentials in molecular crystals, Modelling Simul. Mater. Sci. Eng. 10, R1-R29; J. D. Dunitz and A. Gavezzotti (2005), Molecular recognition in organic crystals: directed intermolecular bonds or nonlocalized bonding? Angew. Chem. Int. Ed. 44, 1766-1787 [doi:10.1002/anie.200460157].
(g) A quick reference monograph on the nature of intermolecular forces is M. Rigby, E. B. Smith, W. A. Wakeham and G. C. Maitland, The Forces between Molecules, Oxford: Clarendon Press (1986). The principles and the early stages of the empirical fitting of potential functions for organic crystals, and their use in lattice statics and dynamics, has been reviewed by A. J. Pertsin and A. I. Kitaigorodski, The Atom-Atom Potential Method, Berlin: Springer Verlag (1987).
(h) Studies of hydrogen bonding have been reviewed and analyzed in many books and monographs; a classic one is G. C. Pimentel and A. L. McClellan, The Hydrogen Bond, San Francisco: Freeman & Co. (1960); a more recent one is by G. A. Jeffrey and W. Saenger, Hydrogen Bonding in Biological Structures, Berlin: Springer Verlag (1991).
(i) A collection of over 1000 heats of sublimation for organic compounds has been given by J. S. Chickos, in Molecular Structure and Energetics, vol. 2, edited by J. F. Liebman and A. Greenberg, New York: VCH (1987). Such compilations may seem uninspiring, but quantitative measurements are the only sound basis of quantitative understanding. See also http://webbook.nist.gov/.
(j) For attempts at the computer prediction of the crystal structure of organic compounds see J. P. M. Lommerse, W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Gavezzotti, D. W. M. Hofmann, F. J. J. Leusen, W. T. M. Mooij, S. L. Price, B. Schweizer, M. U. Schmidt, B. P. van Eijck, P. Verwer and D. E. Williams (2000), A test of crystal structure prediction of small organic molecules, Acta Cryst. B56, 697-714 [doi:10.1107/S0108768100004584]; W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Dzyabchenko, P. Erk, A. Gavezzotti, D. W. M. Hofmann, F. J. J. Leusen, J. P. M. Lommerse, W. T. M. Mooij, S. L. Price, H. Scheraga, B. Schweizer, M. U. Schmidt , B. P. van Eijck, P. Verwer and D. E. Williams (2002), Crystal structure prediction of small organic molecules: a second blind test, Acta Cryst. B58, 647-661 [doi:10.1107/S0108768102005669].
(k) A classical study of the chemical consequences of crystal symmetry is in Chemical consequences of the polar axis in organic solid-state chemistry, D. Y. Curtin and I. C. Paul (1981), Chem. Rev. 81, 525-541 [doi:10.1021/cr00046a001].
(l) On NMR spectroscopy, see C. A. Fyfe, Solid State NMR for Chemists, Guelph, Ontario: CFC Press, (1983).
(m) For those who wish to understand more about the way chirality plays a role in crystal structures and the molecules forming them, the book by J. Jacques, A. Collet, and S. Wilen, Enantiomers, Racemates and Resolutions, New York: Wiley (1981) is a prime source of information nicely written and presented. Other useful texts are H. D. Flack (2003), Chiral and achiral crystal structures, Helv. Chim. Acta, 86, 905-921 [doi:10.1002/hlca.200390109] and H. D. Flack and G. Bernardinelli (2003), The Mirror of Galadriel: looking at chiral and achiral crystal structures, Cryst. Eng. 6, 213-223 [doi:10.1016/j.cryseng.2003.10.001].
(n) For a recent book on polymorphism, see J. M. Bernstein, Polymorphism in Molecular Crystals, Oxford University Press (2002).
- ... molecules1
- From now on, the term molecule denotes a molecule proper, or any other chemical entity also recognizable in the gas phase (a helium atom, an Na+ or SO42- ion, an Fe2(CO)9 complex). In general, it can be said that a molecule is a distinguishable entity when the forces acting within it are much stronger than the forces acting on it in the crystal. Difficulties arise with infinite strings or layers; diamond and NaCl crystals are examples of three-dimensionally infinite systems where the term molecule is meaningless. Also, whenever organic compounds are mentioned in the text, one should read organic and organometallic compounds.
- ... symmetry2
- The term crystal symmetry refers to microscopic relationships between molecules or parts of molecules, and not to macroscopic morphology.
- ... coefficient3
- The packing coefficient is the ratio of volume occupied by the molecules in the cell to the volume of the cell. Molecular volumes can be calculated in a number of ways; the simplest ones are described by Kitaigorodski[5], and others by Gavezzotti[7].
- ... elements4
- A symmetry operation moves or maps isometrically one point to another. A symmetry element is a geometric object, viz a point, a line or a plane, assigned specifically to a set containing one or several symmetry operations. The distinction between a symmetry operation and a symmetry element is explained in detail in the opening chapters of International Tables for Crystallography Vol. A[10].