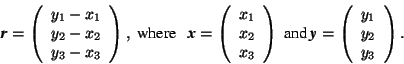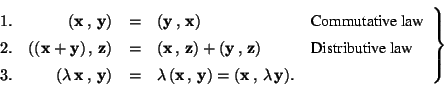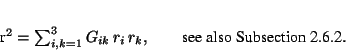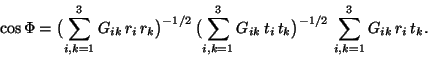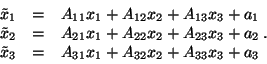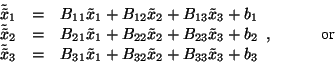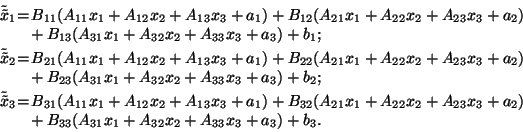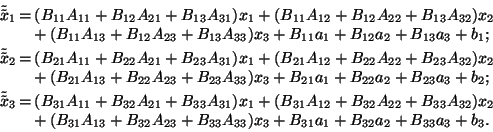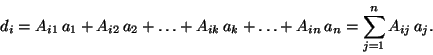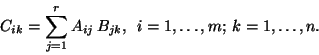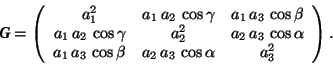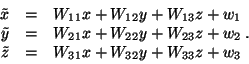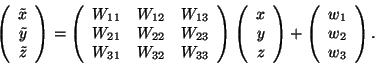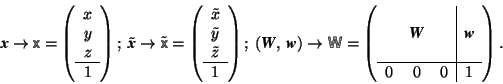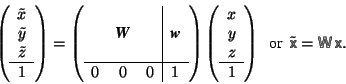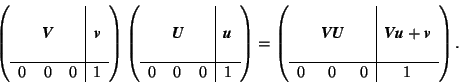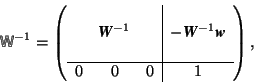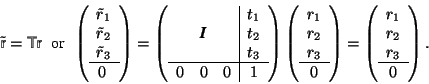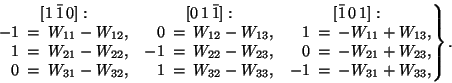Matrices, mappings, and crystallographic symmetry
Hans Wondratschek
Institut für Kristallographie, Universität Karlsruhe, Germany
-
Preface
Part I. Points, vectors, and matrices
-
Points and vectors
- Points and their coordinates
- Special coordinate systems: Cartesian coordinates
- Vectors
- Vector coefficients
- The scalar product and special bases
- Distances and angles
-
Matrices and determinants
- Mappings and symmetry operations
- Motivation
- The matrix formalism
- Rules for matrix calculations
- Determinants
- Applications
Part II. Crystallographic applications
-
Crystallographic symmetry
- Isometries
- Crystallographic site-symmetry operations
- Space-group operations
- Crystallographic groups
- Display of crystallographic symmetry in IT A
-
The description of mappings by matrix-column pairs
- Matrix-column pairs
- Combination and reversion of mappings
- (
 ) matrices
) matrices - Transformation of vector coefficients
- The matrix-column pairs of crystallographic symmetry operations
- The 'General Position' in IT A
-
Special aspects of the matrix formalism
-
Solution of the exercises
- Index
Preface
This pamphlet is based on the manuscript for a summer school in Suez, Egypt, in April 1997. Part I describes some elementary mathematics, similar to the manuscript that was distributed to the school participants in advance of the school. It is intended to remind the readers of selected mathematical concepts. Part II contains the material that was covered in my six lectures and three exercise sessions at the school. A carefully prepared Index is included for quick references.In the analytical description of crystallographic symmetry, group theory is an instrument of utmost importance. Regrettably, there was no time to introduce group theory during the school. The group-theoretical aspects of crystallography could only be mentioned occasionally but not treated systematically. Therefore, also in this pamphlet emphasis was put onto matrix methods. These are considered to be more basic from the point of view of applications. The group-theoretical methods can lead to a deeper insight into the crystallographic concepts and their relationships later.
I very much enjoyed the interest of the participants and the stimulating discussions with them and the other lecturers. The results of these discussions are taken into account in this manuscript. I should like to thank in particular the chair of the school, Karimat El-Sayed, as well as Farid Ahmed for their advice before, and Jenny Glusker and Farid Ahmed for improving the final version of this article. Brian McMahon has helped me with his technical expertise.
List of symbols
| vectors | |
| point coordinates, vector coefficients, or coefficients of the translation part of a mapping | |
| column of point coordinates, of vector coefficients, or of the translation part of a mapping | |
| image point, its column of coordinates, and its coordinates | |
| x |
column of coordinates and coordinates in a new coordinate system |
| A, I, W | mappings |
|---|---|
| matrix coefficients | |
| (A,a), (W,w) | matrix-column pairs |
| row of basis vectors | |
| row of vector coefficients | |
| A |
transposed matrix |
| G, G |
fundamental matrix and its coefficients |
| lattice constants | |
| angles between the basis vectors | |
| angle between two vectors (bond angle) | |
| det |
determinant of a matrix |
| groups | |
| augmented matrix and columns |
The International Tables for Crystallography, Vol. A (1983), 4th edition (1995), will be abbreviated 'IT A'.
Points and vectors
In this chapter, points and vectors are introduced. In spite of their strong relations, the difference between these concepts is emphasized. The distinction between them is sometimes not easy because both items are mostly described in the same way, namely by columns of coefficients. Indeed, it is often not necessary to know the real meaning of such columns, and they can be treated in the same way independently of their nature. Sometimes, however, their behaviour is different and their distinction is necessary for a real understanding of the description of crystallographic objects and to avoid mistakes.
Points and their coordinates
A mathematical model of the space in which we live is the point space. Its elements are points. Objects in point space may be single points; finite sets of points, e.g. the centers of the atoms of a molecule; infinite discontinuous point sets, e.g. the centers of the atoms of an ideal (infiniely extended and periodic) crystal pattern; continuous point sets like straight lines, curves, planes, curved surfaces, to mention just a few which play a role in crystallography.
In the following we restrict our considerations to the 3-dimensional space. The transfer to the plane should be obvious. One can even extend the whole concept to n-dimensional space with arbitrary dimension n.
In order to describe the objects in point space analytically, one introduces a coordinate system. To achieve this, one selects some point as the origin O. Then one chooses three straight lines running through the origin and not lying in a plane. They are called the coordinate axes ![]() ,
, ![]() , and
, and ![]() or
or ![]() ,
, ![]() , and
, and ![]() . On each of these lines a point different from O is chosen marking the unit on that axis:
. On each of these lines a point different from O is chosen marking the unit on that axis: ![]() on
on ![]() ,
, ![]() on
on ![]() , and
, and ![]() on
on ![]() . An arbitrary point P is then described by its coordinates
. An arbitrary point P is then described by its coordinates ![]() ,
, ![]() ,
, ![]() or
or ![]() ,
, ![]() ,
, ![]() , see Fig.1.1.1:
, see Fig.1.1.1:
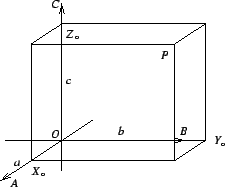 |
Definition (D 1.1.3) The parallel coordinates x, y, and z or ![]() ,
, ![]() , and
, and ![]() of an arbitrary point P are defined in the following way:
of an arbitrary point P are defined in the following way:
- The origin O is the point with the coordinates 0,0,0.
- One constructs the 3 planes through the point
 which are parallel to the pairs of axes
which are parallel to the pairs of axes  and
and 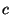 ,
, 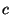 and
and 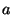 , and
, and 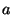 and
and 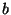 , respectively. These 3 planes intersect the coordinate axes
, respectively. These 3 planes intersect the coordinate axes 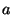 ,
, 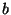 , and
, and 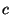 in the points
in the points 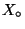 ,
, 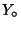 , and
, and 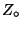 , respectively.
, respectively. - The fractions of the lengths
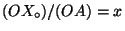 on the axis
on the axis 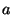 ,
,
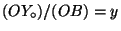 on
on 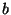 , and
, and 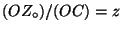 on
on  are the coordinates of the point P.
are the coordinates of the point P.
In this way one assigns uniquely to each point a triplet of coordinates and vice versa. In crystallography the coordinates are written usually in a column which is designated by a boldface-italics lower-case letter, e.g.,
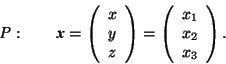
Definition (D 1.1.3) The set of all columns of three real numbers represents all points of the point space and is called the affine space.
The affine space is not yet a good model for our physical space. In reality one can measure distances and angles which is possible in the affine space only after the introduction of a scalar product, see Sections 1.5 and 1.6. Such a space with a scalar product is the fundament of the following considerations.
Definition (D 1.1.3) An affine space, for which a scalar product is defined, is called a Euclidean space.
The coordinates of a point P depend on the position of P in space as well as on the coordinate system. The coordinates of a fixed point P are changed by another choice of the coordinate axes but also by another choice of the origin. Therefore, the comparison of two points by their columns of coordinates is only possible if the coordinate system is the same to which these points are referred. Two points are equal if and only if their columns of coordinates agree in all coordinates when referred to the same coordinate system. If points are referred to different coordinate systems and if the relations between these coordinate systems are known then one can recalculate the coordinates of the points by a coordinate transformation in order to refer them to the same coordinate system, see Subsection 5.3.3. Only after this transformation a comparison of the coordinates is meaningful.
Special coordinate systems: Cartesian coordinates
There are different types of coordinate systems. Coordinate systems with straight lines as axes as introduced in Section 1.1 are called parallel coordinates. In physics polar coordinates in the plane and cylindrical or spherical coordinates in the space are used frequently depending on the kind of problems.
In general those coordinates are chosen in which the solution of the given problem is expected to cause the least difficulties. We shall consider mainly parallel coordinates. Such coordinate systems are of utmost importance for crystallography due to the periodicity of the crystals. In this section a special system with parallel coordinates will be defined which is used frequently in physics, also in crystal physics, and in mathematics. It is applied in Section 1.6. In crystallography, mostly special crystallographic coordinate systems are used.
Definition (D 1.2.1) A coordinate system with 3 coordinate axes perpendicular to each other and lengths ![]() is called a Cartesian coordinate system.
is called a Cartesian coordinate system.
Referring the points to a Cartesian coordinate system simplifies many formulae, e.g. for the determination of distances between points and of angles between lines, and thus makes such calculations particularly easy, cf. Sections 1.6 and 2.6. On the other hand, the description of the symmetry of crystals, in particular of the translational symmetry (also in reciprocal space) becomes quite involved when using Cartesian coordinates. With the exception of crystal physics, the disadvantages of Cartesian coordinates outweigh their advantages when dealing with crystallographic problems.
Vectors
Vectors are objects which are encountered everywhere in crystallography: as distance vectors between atoms, as basis vectors of the coordinate system, as translation vectors of a crystal lattice, as vectors of the reciprocal lattice, etc. They are elements of the vector space which is studied by linear algebra and is an abstract space. However, vectors can be interpreted easily visually, see Fig.1.3.1:
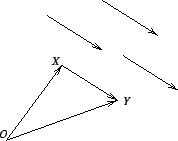 |
For each pair of points X and Y one can draw the arrow ![]() from X to Y. The arrow
from X to Y. The arrow ![]() is a representation of the vector r, as is any arrow of the direction and length of r, see Fig. 1.3.1. The set of all vectors forms the vector space. The vector space has no origin but instead there is the zero vector or o vector
is a representation of the vector r, as is any arrow of the direction and length of r, see Fig. 1.3.1. The set of all vectors forms the vector space. The vector space has no origin but instead there is the zero vector or o vector ![]() which is obtained by connecting any point
which is obtained by connecting any point ![]() with itself. The vector r has a length which is designed by
with itself. The vector r has a length which is designed by ![]() , where r is a non-negative real number. This number is also called the absolute value of the vector. A formula for the calculation of
, where r is a non-negative real number. This number is also called the absolute value of the vector. A formula for the calculation of ![]() can be found in Sections 1.6 and 2.6.
can be found in Sections 1.6 and 2.6.
For such vectors some simple rules hold which can be visualized, e.g. by a drawing in the plane:
- If
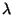 is a real number then the vector
is a real number then the vector 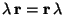 is defined as the vector parallel to r and with length
is defined as the vector parallel to r and with length 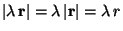 .
.
In particular,
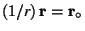 is a vector of length 1. Such a vector is called a unit vector. Further
is a vector of length 1. Such a vector is called a unit vector. Further 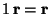 ;
; 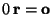 is the zero-vector with length 0. It is the only vector with no direction.
is the zero-vector with length 0. It is the only vector with no direction. 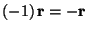 is that vector which has the same length as r,
is that vector which has the same length as r, 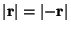 , but opposite direction.
, but opposite direction. - For successive multiplication with the real numbers
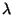 and
and 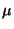 , the relation
, the relation
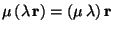 holds.
holds. - For 2 real numbers,
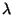 and
and 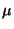 ,
, 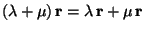 holds.
holds. - For 2 vectors, r and s,
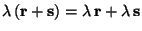 holds.
holds. - For 2 vectors, r and s,
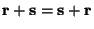 holds. This is called the commutative law of vector addition, see Fig.1.3.2 which is also called the parallelogram of forces. In particular,
holds. This is called the commutative law of vector addition, see Fig.1.3.2 which is also called the parallelogram of forces. In particular, 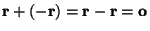 .
. - For any 3 vectors, r, s, and t, the associative law of vector addition, see Fig.1.3.3,
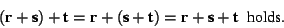
Fig. 1.3.2 Visualization of the commutative law of vector addition:
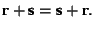
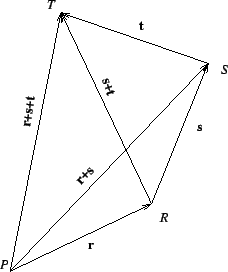 Fig. 1.3.3 Visualization of the associativity of vector addition:
Fig. 1.3.3 Visualization of the associativity of vector addition:
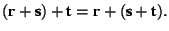
Definition (D 1.3.2) A set of ![]() vectors
vectors ![]() ,
, ![]() , ...,
, ..., ![]() is called linearly independent if the equation
is called linearly independent if the equation
In the plane any 3 vectors r![]() , r
, r![]() , and r
, and r![]() are linearly dependent because coefficients
are linearly dependent because coefficients ![]() can always be found such that
can always be found such that ![]() not all zero and
not all zero and
Definition (D 1.3.2) The maximal number of linearly independent vectors in a vector space is called the dimension of the space.
As is well known, the dimension of the plane is 2, of the space is 3. Any 4 vectors in space are linearly dependent. Thus, if there are 3 linearly independent vectors r![]() , r
, r![]() , and r
, and r![]() , then any other vector r can be represented in the form
, then any other vector r can be represented in the form ![]()
Such a representation is widely used, it will be considered in the next section.
Vector coefficients
We start this section with a definition.
Definition (D 1.4.1) A set of 3 linearly independent vectors r![]() , r
, r![]() , and r
, and r![]() in space is called a basis of the vector space. Any vector r of the vector space can be written in the form
in space is called a basis of the vector space. Any vector r of the vector space can be written in the form ![]() . The vectors r
. The vectors r![]() , r
, r![]() , and r
, and r![]() are called basis vectors; the vector r is called a linear combination of r
are called basis vectors; the vector r is called a linear combination of r![]() , r
, r![]() , and r
, and r![]() . The real numbers
. The real numbers ![]() ,
, ![]() , and
, and ![]() are called the coefficients of r with respect to the basis r
are called the coefficients of r with respect to the basis r![]() , r
, r![]() , r
, r![]() . In crystallography the 2 basis vectors for the plane are mostly called a and b or
. In crystallography the 2 basis vectors for the plane are mostly called a and b or ![]() and
and ![]() , and the 3 basis vectors of the space are a, b, and c or
, and the 3 basis vectors of the space are a, b, and c or ![]() ,
, ![]() , and
, and ![]() .
.
The vector ![]() connects the points
connects the points ![]() and
and ![]() , see Fig. 1.3.1. In Section 1.1 the coordinates
, see Fig. 1.3.1. In Section 1.1 the coordinates ![]() ,
, ![]() , and
, and ![]() of a point
of a point ![]() have been introduced, see Fig. 1.1.1. We now replace the section
have been introduced, see Fig. 1.1.1. We now replace the section ![]() on the coordinate axis
on the coordinate axis ![]() by the vector
by the vector ![]() ,
, ![]() on
on ![]() by
by ![]() , and
, and ![]() on
on ![]() by
by ![]() . If
. If ![]() and
and ![]() are given by their columns of coordinates with respect to these coordinate axes, then the vector
are given by their columns of coordinates with respect to these coordinate axes, then the vector ![]() is determined by the column of the three coordinate differences between the points
is determined by the column of the three coordinate differences between the points ![]() and
and ![]() . These differences are the vector coefficients of r:
. These differences are the vector coefficients of r:
As the point coordinates, the vector coefficients are written in a column. It is not always obvious whether a column of 3 numbers represents a point by its coordinates or a vector by its coefficients. One often calls this column itself a 'vector'. However, this terminology should be avoided. In crystallography both, points and vectors are considered. Therefore, a careful distinction between both items is necessary.
An essential difference between the behaviour of vectors and points is provided by the changes in their coefficients and coordinates if another origin ![]() in point space is chosen:
in point space is chosen:
Let ![]() be the new,
be the new, ![]() the old origin, and o
the old origin, and o![]() the column of coordinates of
the column of coordinates of ![]() with respect to the old coordinate system:
with respect to the old coordinate system: 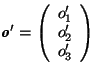 .
.
Then 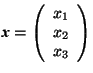 and
and 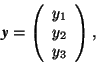 the coordinates of
the coordinates of ![]() and
and ![]() in the old coordinate system, are replaced by the columns
in the old coordinate system, are replaced by the columns 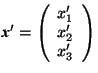 and
and 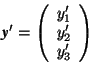 of the coordinates in the new coordinate system, see Fig.1.4.1.
of the coordinates in the new coordinate system, see Fig.1.4.1.
From ![]() follows
follows ![]() and
and ![]() , etc. Therefore, the coordinates of the points change if one chooses a new origin.
, etc. Therefore, the coordinates of the points change if one chooses a new origin.
However, the coefficients of the vector ![]() do not change because of
do not change because of ![]() , etc.
, etc.
![Fig. 1.4.1]](https://www.iucr.org/__data/assets/image/0016/15118/orig.gif) |
| Fig. 1.4.1 The coordinates of the points |
The rules 1., 2., and 5. of Section 1.3 (the others are then obvious) are expressed by:
- The vector x is multiplied with a real number
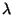
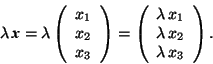
- For successive multiplication of x with
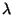 and
and 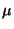
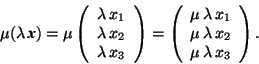
- The sum
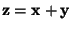 of two vectors is calculated by their columns x and y
of two vectors is calculated by their columns x and y
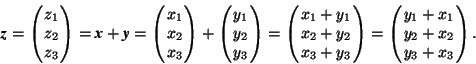
The scalar product and special bases
In order to express the angle between two vectors the scalar product is now introduced. In this way also the bases can be characterized by their lattice constants.
Definition (D 1.5.3) The scalar product (x,y) between two vectors x and y is defined by (x,y) = ![]()
For the scalar product the following rules hold:
Special cases.
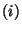
- Because of
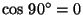 the scalar product is zero if its vectors are perpendicular to each other. Therefore, a scalar product may be zero even if none of the vectors is the o vector.
the scalar product is zero if its vectors are perpendicular to each other. Therefore, a scalar product may be zero even if none of the vectors is the o vector. 
- If x = y, then because of
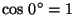 the scalar product is the square of the absolute value of x:
the scalar product is the square of the absolute value of x: 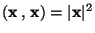 .
.
Two types of special bases shall be considered in this section.
The first one is the basis underlying the Cartesian coordinate system, see Section 1.2. It has the property that the scalar products between different basis vectors are always zero: ![]() for
for ![]() ,
, ![]() , because the basis vectors are perpendicular to each other. In addition,
, because the basis vectors are perpendicular to each other. In addition, ![]() for any
for any ![]() because the basis vectors have unit length. Such a basis is called an orthonormal basis. An orthonormal basis allows simple calculations of distances and bonding angles, see the next section.
because the basis vectors have unit length. Such a basis is called an orthonormal basis. An orthonormal basis allows simple calculations of distances and bonding angles, see the next section.
The other bases are those which are mostly used in crystallography. Real crystals in the physical space may be idealized by crystal patterns which are 3-dimensional periodic sets of points representing, e.g., the centers of the atoms of the crystal. Because of the periodicity of the crystal pattern there are translations which map the crystal pattern onto itself (often expressed by 'the crystal pattern is left invariant under the translation'). We consider these translations. If each of successive translations leaves the crystal pattern invariant, then so does that translation which results from the combination of the successive translations.
To each translation there belongs a translation vector. To the resulting translation belongs that vector which is the sum of the vectors of the performed successive translations. This means that for any set of translation vectors, all their integer linear combinations are translation vectors of symmetry translations of the crystal pattern as well.
Due to the finite size of the atoms the symmetry translations of a crystal pattern can not be arbitrarily short, there must be a minimum length (of a few Å). We choose three shortest translation vectors a![]() , a
, a![]() , and a
, and a![]() which do not lie in a plane, i.e. which are linearly independent. Then any integer linear combination
which do not lie in a plane, i.e. which are linearly independent. Then any integer linear combination ![]() ,
, ![]() integer, of a
integer, of a![]() , a
, a![]() , and a
, and a![]() is a translation vector of a symmetry translation as well. One can show that no other translation vector may belong to a symmetry translation.
is a translation vector of a symmetry translation as well. One can show that no other translation vector may belong to a symmetry translation.
Definition (D 1.5.3) The set of all translation vectors belonging to symmetry translations of a crystal pattern is called the vector lattice of the crystal pattern (and of the real crystal). Its vectors are called lattice vectors. A basis of 3 linearly independent lattice vectors is called a lattice basis. If all lattice vectors are integer linear combinations of the basis vectors, then the basis is called a primitive lattice basis or a primitive basis.
![\psfig{figure=strule.eps,width=3cm}%%\rule[-7ex]{0em}{8ex}](https://www.iucr.org/__data/assets/image/0004/15178/img155.gif) |
![\psfig{figure=struri.eps,width=3cm}%%\rule[-7ex]{0em}{8ex}](https://www.iucr.org/__data/assets/image/0005/15179/img156.gif) |
| Fig. 1.5.1 Finite part of a planar 'crystal structure' (left) with the corresponding vector lattice (right). The dots mark the end points of the vectors. |
Several bases are drawn in the right part of Fig. 1.5.1. Four of them are primitive, among them the one which consists of the two shortest linearly independent lattice vectors (lower left corner). The upper right basis is not primitive.
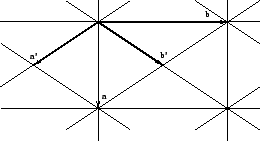 |
| Fig. 1.5.2 c-centered lattice (net) in the plane with conventional a, b and primitive a', b' bases. |
Remarks.
- If the vectors a
 , a
, a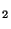 , and a
, and a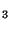 or a, b, and c form a lattice basis, then any integer linear combination of the basis vectors is a lattice vector as well. However, there may be other vectors with rational non-integer coefficients which are also lattice vectors. In this case crystallographers speak of a centered lattice although not the lattice is centered but only the basis is chosen such that the lattice appears to be centered.
or a, b, and c form a lattice basis, then any integer linear combination of the basis vectors is a lattice vector as well. However, there may be other vectors with rational non-integer coefficients which are also lattice vectors. In this case crystallographers speak of a centered lattice although not the lattice is centered but only the basis is chosen such that the lattice appears to be centered.
Example, see Fig.1.5.2. The lattice type c in the plane with conventional basis a, b consists of all vectors v =
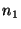 a +
a + 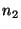 b and v = (
b and v = (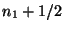 )a + (
)a + (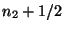 )b,
)b, 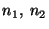 integer. This basis is a lattice basis but not a primitive one.
integer. This basis is a lattice basis but not a primitive one.The basis a' = a/2 - b/2, b' = a/2 + b/2 would be a primitive basis. Referred to this basis all lattice vectors have integer coefficients.
- For any lattice a primitive basis may be chosen (for each lattice in the plane or in the space there even exists an infinite number of primitive bases). The basis chosen in IT A for the description of a lattice is called the conventional basis. If the conventional basis is primitive, then also the lattice is called primitive. For other reasons, the conventional basis is frequently non-primitive such that the lattice appears to be centered. The conventional centerings are c in the plane and C, A, B, I, F, or
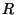 in the space.
in the space. - In higher dimensions (dimension
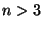 ) the condition that the basis vectors are shortest is no longer sufficient to guarantee a primitive basis.
) the condition that the basis vectors are shortest is no longer sufficient to guarantee a primitive basis.
Let a![]() be a basis. Then one can form the scalar products (a
be a basis. Then one can form the scalar products (a![]() ,a
,a![]() ) between the basis vectors,
) between the basis vectors, ![]() ,
, ![]() = 1, 2, 3. Because (a
= 1, 2, 3. Because (a![]() ,a
,a![]() ) = (a
) = (a![]() ,a
,a![]() ), there are only 6 different scalar products.
), there are only 6 different scalar products.
Definition (D 1.5.3) The quantities
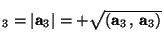 ,
,
![]() ,
, ![]() ,
,
are called the lattice constants of the lattice.
The lengths of the basis vectors are mostly measured in Å (1 Å= 10![]() m), sometimes in pm (1 pm = 10
m), sometimes in pm (1 pm = 10![]() m) or nm (1 nm = 10
m) or nm (1 nm = 10![]() m). The lattice constants of a crystal are given by its translations, more exactly, by the translation vectors of the crystal pattern, they can not be chosen arbitrarily. They may be further restricted by the symmetry of the crystal.
m). The lattice constants of a crystal are given by its translations, more exactly, by the translation vectors of the crystal pattern, they can not be chosen arbitrarily. They may be further restricted by the symmetry of the crystal.
Normally the conventional crystallographic bases are chosen when describing a crystal structure. Referred to them the lattice of a crystal pattern may be primitive or centered. If it is advantageous in exceptional cases to describe the crystal with respect to another basis then this choice should be carefully stated in order to avoid misunderstandings.
Distances and angles
When considering crystal structures, idealized as crystal patterns, frequently the values of distances between the atoms (bond lengths) and of the angles between atomic bonds (bonding angles) are wanted. These quantities can not be calculated from the coordinates of the points (centers of the atoms) directly. Distances and angles are independent of the choice of the origin but the point coordinates depend on the origin choice, see Section 1.4. Therefore, bond distances and angles can only be calculated using the vectors (distance vectors) between the points participating in the bonding. In this section the necessary formulae for such calculations will be derived.
We assume the crystal structure to be given by the coordinates of the atoms (better: of their centers) in a conventional coordinate system. Then the vectors between the points can be calculated by the differences of the point coordinates.
Let ![]() be the vector from point
be the vector from point ![]() to point
to point ![]() ,
, ![]() , see equation 1.4.1. The scalar product
, see equation 1.4.1. The scalar product ![]() of r with itself is the square of the length
of r with itself is the square of the length ![]() of r. Thus
of r. Thus
Using this equation, bond distances can be calculated if the coefficients of the bond vector and the lattice constants of the crystal are known.
The general formula (1.6.1) becomes much simpler for the higher symmetric crystal systems. For example, referred to an orthonormal basis, equation (1.6.1) is reduced to
Using the ![]() sign and abbreviating
sign and abbreviating ![]() (
(![]() is defined for
is defined for ![]() : then
: then ![]() ), this formula can be written
), this formula can be written
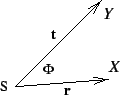
| Fig. 1.6.1 The bonding angle |
The (bonding) angle ![]() between the (bond) vectors
between the (bond) vectors ![]() and
and ![]() is calculated using the equation
is calculated using the equation
One obtains
Again one can use the coefficients ![]() to obtain, see also Subsection 2.6.2,
to obtain, see also Subsection 2.6.2,
For orthonormal bases, equation (1.6.4) is reduced to
| (1.6.6) |
and equation 1.6.5 is replaced by
Matrices and determinants
The second chapter deals with matrices and determinants which are essential for the analytical description of crystallographic symmetry. Matrices are mathematical tools which may simplify involved calculations considerably and may make complex formulae transparent. One can introduce them in an abstract way as a formalism and then apply them to many calculations in crystallography. However, it seems to be better first to justify their introduction. Determinants are used for the calculation of the volume, e.g. of a unit cell from the lattice constants, or in the process of inverting a matrix.
Mappings and symmetry operations
In crystallography, mapping an object of point space, e.g. the atomic centers of a molecule or a crystal pattern, is one of the most basic procedures. Most crystallographic mappings are rather special. Nevertheless, the term 'mapping' will be introduced first in a more general way. What is a mapping of, e.g., a set of points ?
Definition (D 2.1.1) A mapping of a set ![]() into a set
into a set ![]() is a relation such that for each element
is a relation such that for each element ![]() there is a unique element
there is a unique element ![]() which is assigned to
which is assigned to ![]() . The element
. The element ![]() is called the image of
is called the image of ![]() .
.
 |
| Fig. 2.1.1 The relation of the point |
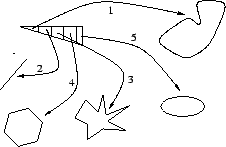 |
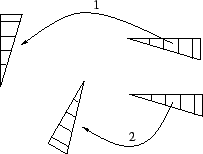
The mapping which is displayed in Fig. 2.1.2 is rather complicated and can hardly be described analytically. The mappings which are mainly used in crystallography are much simpler: In general they map closed regions onto closed regions. Although distances between points or angles between lines may be changed, parallel lines of the original figure are always parallel also in the image. Such mappings are called affine mappings. An affine mapping will in general distort an object, e.g. by a shearing action or by an (isotropic or anisotropic) shrinking, see Fig. 2.1.3. For example, in the space a cube may be distorted by an affine mapping into an arbitrary parallelepiped but not into an octahedron or tetrahedron.
 |
If an affine mapping leaves all distances and thus all angles invariant, it is called isometric mapping, isometry, motion, or rigid motion. We shall use the name 'isometry'. An isometry does not distort but moves the undistorted object through the point space. However, it may change the orientation of an object, e.g. transfer a right glove into an (otherwise identical) left one. Different types of isometries are distinguished: In the space these are translations, rotations, inversions, reflections, and the more complicated roto-inversions, screw rotations, and glide reflections.
 |
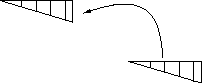 |
| Fig. 2.1.5 A parallel shift of the triangle is called a translation. Translations are special isometries. They play a distinguished role in crystallography. |
One of the outstanding concepts in crystallography is 'symmetry'. An object has symmetry if there are isometries which map the object onto itself such that the mapped object can not be distinguished from the object in the original state. The isometries which map the object onto itself are called symmetry operations of this object. The symmetry of the object is the set of all its symmetry operations. If the object is a crystal pattern, representing a real crystal, its symmetry operations are called crystallographic symmetry operations.
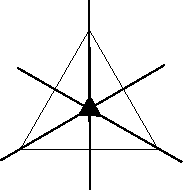 |
| Fig. 2.1.6 The equilateral triangle allows six symmetry operations: rotations by |
Motivation
Any isometry may be the symmetry operation of some object, e.g. of the whole space, because it maps the whole space onto itself. However, if the object is a crystal pattern, due to its periodicity not every rotation, roto-inversion, etc. can be a symmetry operation of this pattern. There are certain restrictions which are well known and which are taught in the elementary courses of crystallography.
How can these symmetry operations be described analytically ? Having chosen a coordinate system with a basis and an origin, each point of space can be represented by its column of coordinates. A mapping is then described by the instruction, in which way the coordinates ![]() of the image point
of the image point ![]() can be obtained from the coordinates x of the original point X:
can be obtained from the coordinates x of the original point X:
The functions ![]() are not restricted for an arbitrary mapping. However, for an affine mapping the functions
are not restricted for an arbitrary mapping. However, for an affine mapping the functions ![]() are very simple: An affine mapping
are very simple: An affine mapping ![]() is always represented in the form
is always represented in the form
A second mapping which brings the point ![]() is then represented by
is then represented by
The equations (2.2.3) may be rearranged in the following way:
Although straightforward, one will agree that this is not a comfortable way to describe and solve the problem of combining mappings. Matrix formalism does nothing else than to formalize what is being done in equations (2.2.1) to (2.2.4), and to describe this procedure in a kind of shorthand notation, called the matrix notation:
The matrix notation for mappings will be dealt with in more detail in Sections 4.1 and 4.2. In the next section the matrix formalism will be introduced.The matrix formalism
Definition (D 2.3.3) A rectangular array of real numbers in ![]() rows and
rows and ![]() columns is called a real (
columns is called a real (![]() ) matrix A:
) matrix A:

The left index, running from 1 to ![]() , is called the row index, the right index, running from 1 to
, is called the row index, the right index, running from 1 to ![]() , is the column index of the matrix. If the elements of the matrix are rational numbers, the matrix is called a rational matrix; if the elements are integers it is called an integer matrix.
, is the column index of the matrix. If the elements of the matrix are rational numbers, the matrix is called a rational matrix; if the elements are integers it is called an integer matrix.
Definition (D 2.3.3) An ![]() matrix is called a square matrix,
matrix is called a square matrix,
an ![]() matrix a column matrix or just a column, and
matrix a column matrix or just a column, and
a ![]() matrix a row matrix or, for short, a row.
matrix a row matrix or, for short, a row.
The index '1' for column and row matrices is often omitted.
Definition (D 2.3.3) Let A be an ![]() matrix. The
matrix. The ![]() matrix which is obtained from A = (
matrix which is obtained from A = (![]() ) by exchanging rows and columns, i.e. the matrix (
) by exchanging rows and columns, i.e. the matrix (![]() ), is called the transposed matrix A
), is called the transposed matrix A ![]() .
.
Example. If 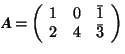 , then
, then 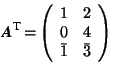 .
.
(Crystallographers frequently write negative numbers ![]() as
as ![]() , e.g. for MILLER indices or elements of matrices).
, e.g. for MILLER indices or elements of matrices).
Remark. In crystallography point coordinates or vector coefficients are written as columns. In order to distinguish columns from rows (the MILLER indices, e.g., are written as rows), rows are regarded as transposed columns and are thus marked by (..) ![]() .
.
General matrices, including square matrices, will be designated by boldface-italics upper case letters A, B, W, ...;
columns by boldface-italics lower case letters a, b, ..., and
rows by (a) ![]() , (b)
, (b) ![]() , ..., see also p.
, ..., see also p. ![[*]](crossref.gif) , List of symbols.
, List of symbols.
A square matrix A is called symmetric if A ![]() = A, i.e. if
= A, i.e. if ![]() holds for any pair
holds for any pair ![]() .
.
A symmetric matrix is called a diagonal matrix if ![]() for
for ![]() .
.
A diagonal matrix with all elements ![]() is called the unit matrix I.
is called the unit matrix I.
A matrix consisting of zeroes only, i.e. ![]() for any pair
for any pair ![]() is called the O-matrix.
is called the O-matrix.
We shall need only the special combinations ![]() 'square matrix';
'square matrix'; ![]() 'column matrix' or 'column' , and
'column matrix' or 'column' , and ![]() 'row matrix' or 'row'. However, the formalism does not depend on the sizes of
'row matrix' or 'row'. However, the formalism does not depend on the sizes of ![]() and
and ![]() . Therefore, and because of other applications, formulae are displayed for general
. Therefore, and because of other applications, formulae are displayed for general ![]() and
and ![]() . For example, in the Least-Squares procedures of X-ray crystal-structure determination huge (
. For example, in the Least-Squares procedures of X-ray crystal-structure determination huge (![]() ) matrices are handled.
) matrices are handled.
Rules for matrix calculations
Matrices can be multiplied with a number or can be added, subtracted, and multiplied with each other. These operations obey the following rules:
Definition (D 2.4.5) An ![]() matrix A is multiplied with a (real) number
matrix A is multiplied with a (real) number ![]() by multiplying each element with
by multiplying each element with ![]() :
:
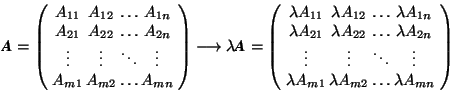 .
.
Definition (D 2.4.5) Let ![]() and
and ![]() be the general elements of the matrices A and B. Moreover, A and B must be of the same size, i.e. must have the same number of rows and of columns. Then the sum and the difference
be the general elements of the matrices A and B. Moreover, A and B must be of the same size, i.e. must have the same number of rows and of columns. Then the sum and the difference ![]() is defined by
is defined by
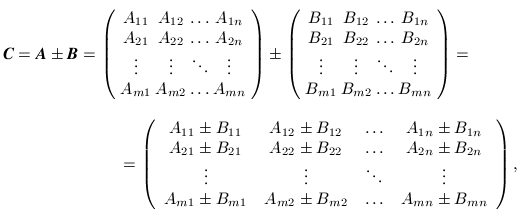
i.e. the element ![]() of C is equal to the sum or difference of the elements
of C is equal to the sum or difference of the elements ![]() and
and ![]() of A and B for any pair of
of A and B for any pair of ![]() :
: ![]() .
.
The definition of matrix multiplication looks more complicated at first sight but it corresponds exactly to what is written in full in the formulae (2.2.1) to (2.2.4) of Section 2.2. The multiplication of two matrices is defined only if the number ![]() of columns of the
of columns of the ![]() ft
ft ![]() trix is the same as the number
trix is the same as the number ![]() of rows of the
of rows of the ![]() ght
ght ![]() trix. The numbers
trix. The numbers ![]() of rows of the
of rows of the ![]() ft
ft ![]() trix and
trix and ![]() of columns of the
of columns of the ![]() ght
ght ![]() trix are free.
trix are free.
We first define the product of a matrix A with a column a:
Definition (D 2.4.5) The multiplication of an (![]() ) matrix A with an (
) matrix A with an (![]() ) column a is only possible if the number
) column a is only possible if the number ![]() of columns of the matrix is the same as the length of the column a. The result is the matrix product d = A
of columns of the matrix is the same as the length of the column a. The result is the matrix product d = A![]() a which is a column of length
a which is a column of length ![]() . The
. The ![]() -th element
-th element ![]() of d is
of d is
Written as a matrix equation this is
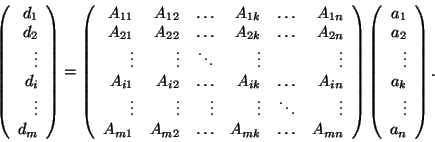
In an analogous way one defines the multiplication of a row matrix with a general matrix.
Definition (D 2.4.5) The multiplication of a ![]() row a
row a ![]() , with an (
, with an (![]() ) matrix A is only possible if the length
) matrix A is only possible if the length ![]() , i.e. the number of 'columns', of the row is the same as the number
, i.e. the number of 'columns', of the row is the same as the number ![]() of rows of the matrix. The result is the matrix product d
of rows of the matrix. The result is the matrix product d ![]() = a
= a ![]() A which is a row of length
A which is a row of length ![]() . The
. The ![]() -th element
-th element ![]() of d
of d ![]() is
is
Written as a matrix equation this is
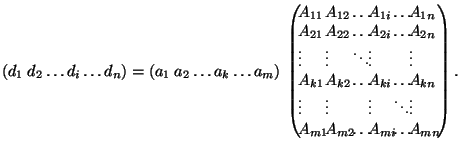
The multiplication of two matrices (both neither row nor column) is the combination of the already defined multiplications of a matrix with a column (matrix on the left, column on the right side) or of a row with a matrix (row on the left, matrix on the right side). Remember: The number of columns of the left matrix must be the same as the number of rows of the right matrix.
Definition (D 2.4.5) The matrix product C = A![]() B, or
B, or
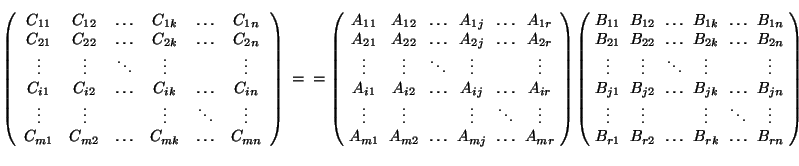
Examples.
If 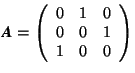 and
and 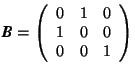 ,
,
then 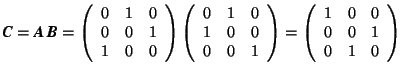 . On the
. On the
other hand, 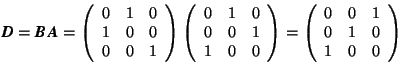 .
.
Obviously, C![]() D, i.e. matrix multiplication is not always commutative. However, it is associative, e.g., (AB)D = A(BD), as the reader may verify by performing the indicated multiplications. One may also verify that matrix multiplication is distributive, i.e.
D, i.e. matrix multiplication is not always commutative. However, it is associative, e.g., (AB)D = A(BD), as the reader may verify by performing the indicated multiplications. One may also verify that matrix multiplication is distributive, i.e.
(A + B)C = AC + BC.
In 'indices notation' (where A is an ![]() matrix, B an
matrix, B an ![]() matrix) the matrix product is
matrix) the matrix product is
Remarks.
- The matrix A has the same number
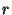 of columns as B has rows; the number
of columns as B has rows; the number 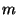 of rows is 'inherited' from A to C, the number
of rows is 'inherited' from A to C, the number 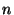 of columns from B to C.
of columns from B to C. - A comparison with equation (2.2.4) shows that exactly the same construction occurs in the matrix product when describing consecutive mappings by matrix-column pairs. Also the product of the matrix B with the column a will be recognized. It is for this reason that the matrix formalism has been introduced. Affine mappings (also isometries and crystallographic symmetry operations) in point space are described by matrix-column pairs, see Sections 2.2 and 4.1.
- The 'power notation' is used in the same way for the matrix product of a square matrix with itself as for numbers: AA = A
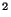 ; AAA = A
; AAA = A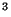 , etc.
, etc. - Using the formulae of this section one confirms equations (2.2.5) to (2.2.8).
Determinants
Matrices are frequently used when investigating the solutions of systems of linear equations. Decisive for the solubility and the possible number of solutions of such a system is a number, called the determinant ![]() or
or ![]() of A, which can be calculated for any
of A, which can be calculated for any ![]() square matrix A. In this section determinants are introduced and some of their laws are stated. Determinants are used to invert matrices and to calculate the volume of a unit cell in Subsections 2.6.1 and 2.6.3.
square matrix A. In this section determinants are introduced and some of their laws are stated. Determinants are used to invert matrices and to calculate the volume of a unit cell in Subsections 2.6.1 and 2.6.3.
The theory of determinants is well developed and can be treated in a very general way. We only need determinants of (2 ![]() 2) and (3
2) and (3 ![]() 3) matrices and will discuss only these.
3) matrices and will discuss only these.
Definition (D 2.5.1)
Let 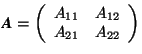 and
and 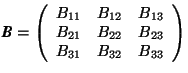 be a
be a
(2 ![]() 2) and a (3
2) and a (3 ![]() 3) matrix. Then their determinants are designated by
3) matrix. Then their determinants are designated by
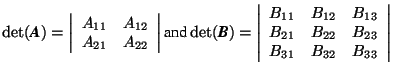 and are defined by the equations
and are defined by the equations
Let D be a square matrix. If ![]() then the matrix D is called regular, if
then the matrix D is called regular, if ![]() , then D is called singular. Here only regular matrices are considered. The matrix W of an isometry W is regular because always
, then D is called singular. Here only regular matrices are considered. The matrix W of an isometry W is regular because always ![]() . In particular,
. In particular, ![]() holds.
holds.
Remark. The determinant ![]() is equal to the fraction
is equal to the fraction ![]() , where
, where ![]() is the volume of an original object and
is the volume of an original object and ![]() the volume of this object mapped by the affine mapping A. Isometries do not change distances, therefore they do not change volumes and
the volume of this object mapped by the affine mapping A. Isometries do not change distances, therefore they do not change volumes and ![]() holds.
holds.
The following rules hold for determinants of ![]() matrices A. The columns of A will be designated for these rules by
matrices A. The columns of A will be designated for these rules by ![]() .
.
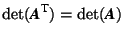 ; the determinant of a matrix is the same as that of the transposed matrix. Because of this rule the following rules, although formulated only for columns, also hold if formulated for rows.
; the determinant of a matrix is the same as that of the transposed matrix. Because of this rule the following rules, although formulated only for columns, also hold if formulated for rows.- If one column of
 is a multiple of another column,
is a multiple of another column, 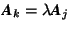 , then
, then 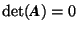 . This implies that
. This implies that 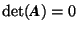 if two columns of A are equal.
if two columns of A are equal. - If a column
 is the sum of two columns
is the sum of two columns  and
and  ,
,  , then
, then 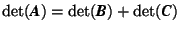 , where B is the matrix which has all columns of A except that
, where B is the matrix which has all columns of A except that  is replaced by
is replaced by 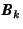 , and C is the matrix with all columns of A except that
, and C is the matrix with all columns of A except that 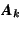 is replaced by
is replaced by 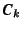 .
. - Exchange of two columns,
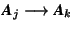 and
and 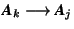 of a determinant changes its sign.
of a determinant changes its sign. - Adding to a column a multiple of another column does not change the value of the determinant:
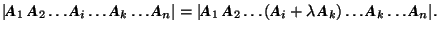
- Multiplication of all elements of a column with a number
 results in the
results in the  -fold value of the determinant:
-fold value of the determinant:
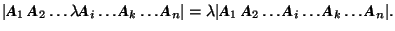
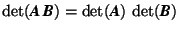 , i.e. the determinant of a matrix product is equal to the product of the determinants of the matrices.
, i.e. the determinant of a matrix product is equal to the product of the determinants of the matrices.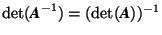 , for
, for 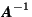 see Subsection 2.6.1.
see Subsection 2.6.1.
Among these rules there are three procedures which do not change the value of the determinant:
- (i)
- transposition;
- (ii)
- an even number of exchanges of columns (or rows correspondingly), because
an odd number of exchanges changes the sign of the determinant; and - (iii)
- adding to a column a multiple of another column (or rows correspondingly).
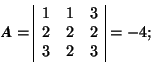
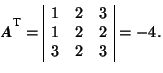
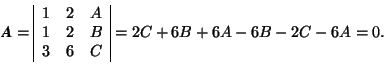
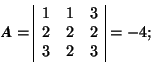
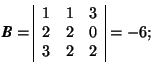
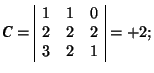
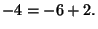
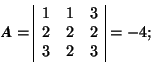
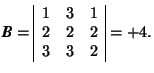
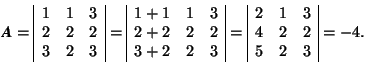
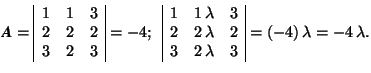
-
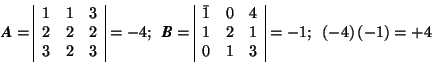
is the product of the determinants.
The determinant of the product AB is
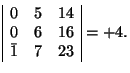
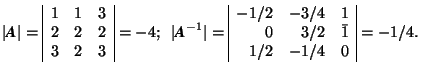
Applications
Only a few applications can be dealt with here:
- The inversion of a matrix;
- Another formula for calculating the distance between points or the angle between lines (bindings);
- A formula for the volume of the unit cell of a crystal.
Inversion of a matrix
The inversion of a square matrix A is a task which occurs everywhere in matrix calculations. Here we restrict the considerations to the inversion of (2 ![]() 2) and (3
2) and (3 ![]() 3) matrices. In Least-Squares refiments the inversion of huge matrices was a serious problem before the computers and programs were sufficiently developed.
3) matrices. In Least-Squares refiments the inversion of huge matrices was a serious problem before the computers and programs were sufficiently developed.
Definition (D 2.6.2) A matrix C which fulfills the condition ![]() for a given matrix A, is called the inverse matrix or the inverse A
for a given matrix A, is called the inverse matrix or the inverse A![]() of A.
of A.
The matrix A![]() exists if and only if
exists if and only if ![]() . In the following we assume C to exist. If
. In the following we assume C to exist. If ![]() then also
then also ![]() holds, i.e. there is exactly one inverse matrix of A. There are two possibilities to calculate the inverse matrix of a given matrix. The first one is particularly simple but not always applicable. The other may be rather tedious but always works.
holds, i.e. there is exactly one inverse matrix of A. There are two possibilities to calculate the inverse matrix of a given matrix. The first one is particularly simple but not always applicable. The other may be rather tedious but always works.
Definition (D 2.6.2) A matrix A is called orthogonal if ![]() .
.
The name comes from the fact that the matrix part of any isometry is an orthogonal matrix if referred to an orthonormal basis. In crystallography most matrices of the crystallographic symmetry operations are orthogonal if referred to the conventional basis.
Procedure: One forms the transposed matrix A ![]() from the given matrix A and tests if it obeys the equation
from the given matrix A and tests if it obeys the equation ![]() . If it does then the inverse
. If it does then the inverse ![]() is found. If not one has to go the general way.
is found. If not one has to go the general way.
There are several general methods to invert a matrix. Here we use a formula based on determinants. It is not restricted to dimensions 2 or 3.
Let A = ![]() be the matrix to be inverted,
be the matrix to be inverted, ![]() its determinant, and A
its determinant, and A![]() =
= ![]() be the inverted matrix which is to be determined. The coefficient
be the inverted matrix which is to be determined. The coefficient ![]() is determined from the equation
is determined from the equation
Note that in this equation the indices of ![]() are exchanged with respect to the element
are exchanged with respect to the element ![]() which is to be determined.
which is to be determined.
Example. Calculate the inverse matrix of 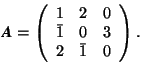
One determines ![]() and obtains for the coefficients of A
and obtains for the coefficients of A![]()
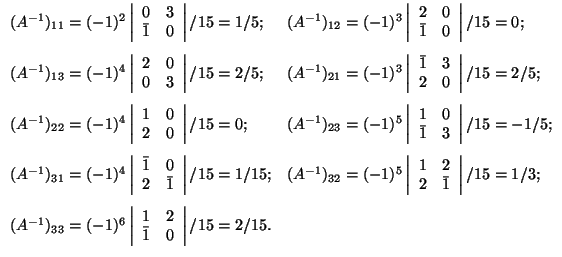
With these coefficients one finds 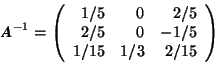
Distances and angles
In Section 1.6 formulae for the distance between points (by calculating the length of a vector) and the angle between bindings (vectors) have been derived. The scalar products of the basis vectors have been designated byfundamental matrix of the coordinate basis 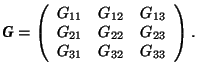
Because of ![]() , G is a symmetric matrix.
, G is a symmetric matrix.
In the formulae of Section 1.6 one may replace the 'index formalism' by the 'matrix formalism'. Using matrix multiplication with rows and columns,
This is the same as equation (1.6.3) but expressed in another way. Such 'matrix formulae' are useful in general calculations when changing the basis, when describing the relation between crystal lattice and reciprocal lattice, etc. However, for the actual calculation of distances, angles, etc. as well as for computer programs, the 'index formulae' of Section 1.6 are more appropriate.
For orthonormal bases, because of G = I equation (2.6.2) becomes very simple:
The formula for the angle ![]() between the vectors (
between the vectors ( ![]() ) = r and (
) = r and ( ![]() ) = t
) = t
The volume of the unit cell
The volume ![]() of the unit cell of a crystal structure, i.e. the body containing all points with coordinates
of the unit cell of a crystal structure, i.e. the body containing all points with coordinates ![]() , can be calculated by the formula
, can be calculated by the formula
In the general case one obtains
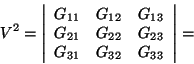
The formula (2.6.6) becomes simpler depending on the crystallographic symmetry, i.e. on the crystal system.
Part II. Crystallographic applications
The mathematical tools which have been developed in the first two chapters of Part I will have useful applications here in Part II; since crystallographic studies require both analytical treatment as well as geometric visualization. Geometric models, perspective drawings, or projections of frames of symmetry, of crystal structures, and of complicated molecules are very instructive. However, often models are difficult to build, perspective drawings become confusing, and projections suffer from loss of information. In addition, distances and angles may be distorted, and it is sometimes not easy to see the important geometric relations.
Analytical methods, e.g. the matrix formalism, provide instruments which are often only slightly dependent on or even independent of the complexity of the subject. In many cases they can be applied using computers. Moreover, there are internal tests which enable the user to check the results of the calculations for inner consistency. Such methods are indispensable in particular in crystal-structure determination and evaluation. Only very simple crystal structures can be considered without them.
Crystallographic symmetry and its applications have been investigated and developed by mineralogists, mathematicians, physicists, and chemists from different countries over several centuries. The result is the beautiful and still rapidly growing tree of contemporary crystallography. However, it is not necessary to know the whole of this field of knowledge in order to apply and to take advantage of it. The crystallographic tools necessary for the exploration of matter and for solid state research can be taken from the volumes of the International Tables for Crystallography series. Symmetry is described in Vol. A of this series. By the manuscript on hand, the reader shall be enabled to use and exploit the contents of that volume A, abbreviated IT A in this manuscript.
Crystallographic symmetry
In this chapter crystallographic symmetry will be outlined in a descriptive way. The general concept of isometries is treated in Section 3.1. The restrictions imposed on crystallographic symmetry operations are dealt with in Sections 3.2 for point-group operations and 3.3 for space-group operations. The chapter is continued with Section 3.4 on crystallographic groups and concluded by Section 3.5 where the non-analytical description of crystallographic symmetry in IT A is dealt with.Isometries
An isometry W, see also Section 2.1,
- maps each point P of the point space onto exactly one image point
 :
: 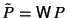 ;
; - is a mapping of the point space onto itself which leaves all distances and thus all angles invariant.
Definition (D 3.1.1) Let W be an isometry and P a point of space. Then P is called a fixed point of the isometry W if it is mapped onto itself (another term: is left invariant) by W, i.e. if the image point ![]() is equal to the original point
is equal to the original point ![]() :
: ![]() .
.
The isometries are classified by their fixed points, and the fixed points are often used to characterize the isometries in visual geometric terms, see the following types of isometries. Besides the 'proper' fixed points there are further objects which are not fixed or left invariant pointwise but only as a whole. Lines and planes of this kind are of great interest in crystallography, see the following examples.
Kinds of isometries.
The kinds 1. to 4. of isometries in the following list preserve the so-called 'handedness' of the objects: if a right (left) glove is mapped by one of these isometries, then the image is also a right (left) glove of equal size and shape. Such isometries are also called isometries of the first kind or proper isometries. The kinds 5. to 8. change the 'handedness': the image of a right glove is a left one, of a left glove is a right one. These kinds of isometries are often called isometries of the second kind or improper isometries.
- Identity I. The identity mapping maps each point onto itself, each point of space is a fixed point. All lines and planes of the space are left invariant as well.
- Translation T. By a translation each point of the point space is shifted in the same direction by the same amount, such that the translation vector r from each original point P to its image point
 is independent of the point P. There is no proper fixed point. Nevertheless, each line L parallel to r is mapped onto itself as a whole, as is each plane which contains L. [The identity mapping may be considered as a special translation with r = o, where o is the zero vector of length zero, see Section 1.3. Except if it is mentioned explicitly, the term 'translation' is used for proper translations only, i.e. for translations with
is independent of the point P. There is no proper fixed point. Nevertheless, each line L parallel to r is mapped onto itself as a whole, as is each plane which contains L. [The identity mapping may be considered as a special translation with r = o, where o is the zero vector of length zero, see Section 1.3. Except if it is mentioned explicitly, the term 'translation' is used for proper translations only, i.e. for translations with  .]
.] - Rotation. Each rotation maps a line of points onto itself pointwise. This line is called the rotation axis. The whole space is rotated around this axis by an angle
 , the rotation angle. The unit vector
, the rotation angle. The unit vector 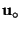 parallel to the rotation axis is called the direction of the rotation axis. Each plane perpendicular to the rotation axis is mapped onto itself as a whole: it is rotated about the intersection point of the plane with the rotation axis. For a 2-fold rotation also each plane containing the rotation axis is left invariant as a whole. [The identity operation may be considered as a special rotation with the rotation angle
parallel to the rotation axis is called the direction of the rotation axis. Each plane perpendicular to the rotation axis is mapped onto itself as a whole: it is rotated about the intersection point of the plane with the rotation axis. For a 2-fold rotation also each plane containing the rotation axis is left invariant as a whole. [The identity operation may be considered as a special rotation with the rotation angle 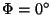 . Except if it is mentioned explicitly, the term 'rotation' is used for proper rotations only, i.e. for rotations with
. Except if it is mentioned explicitly, the term 'rotation' is used for proper rotations only, i.e. for rotations with 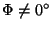 .]
.] - Screw rotation. A screw rotation is a combination of a rotation (
 is the direction of the rotation axis) and a translation with its translation vector parallel to u
is the direction of the rotation axis) and a translation with its translation vector parallel to u . A screw rotation leaves no point fixed, the rotation axis of the involved rotation is called the screw axis, and the vector of the involved translation is the screw vector. The screw axis is not left fixed pointwise but as a whole only (it is shifted parallel to itself by the involved translation). In general the result of the combination of 2 isometries depends on the sequence in which the isometries are performed. The screw rotation, however, is independent of the sequence of its 2 components.
. A screw rotation leaves no point fixed, the rotation axis of the involved rotation is called the screw axis, and the vector of the involved translation is the screw vector. The screw axis is not left fixed pointwise but as a whole only (it is shifted parallel to itself by the involved translation). In general the result of the combination of 2 isometries depends on the sequence in which the isometries are performed. The screw rotation, however, is independent of the sequence of its 2 components. - Inversion. An inversion is the reflection of the whole space in a point
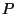 , which is called the center of inversion. The point
, which is called the center of inversion. The point 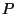 is the only fixed point. Each line or plane through
is the only fixed point. Each line or plane through 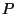 is mapped onto itself as a whole because it is reflected in
is mapped onto itself as a whole because it is reflected in 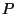 . The inversion is an isometry of the second kind: any right glove is mapped onto a left one and vice versa.
. The inversion is an isometry of the second kind: any right glove is mapped onto a left one and vice versa. - Rotoinversion. A rotoinversion can be understood as a combination of a rotation with
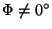 and
and 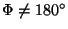 and an inversion, where the center of inversion is placed on the rotation axis of the rotation. A rotoinversion is an isometry of the second kind. The inversion point (which is no longer a center of inversion !) is the only fixed point; the axis of the rotation, now called rotoinversion axis, is the only line mapped onto itself as a whole, and the plane through the inversion point and perpendicular to the rotoinversion axis is the only plane mapped onto itself as a whole. Again, a rotoinversion does not depend on the sequence in which its components are performed.
and an inversion, where the center of inversion is placed on the rotation axis of the rotation. A rotoinversion is an isometry of the second kind. The inversion point (which is no longer a center of inversion !) is the only fixed point; the axis of the rotation, now called rotoinversion axis, is the only line mapped onto itself as a whole, and the plane through the inversion point and perpendicular to the rotoinversion axis is the only plane mapped onto itself as a whole. Again, a rotoinversion does not depend on the sequence in which its components are performed. - Reflection. A reflection is another isometry of the second kind. Each point of space is reflected in a plane, the reflection plane or mirror plane, such that all points of this plane, and only these points, are fixed points. In addition, each line and each plane perpendicular to the mirror plane is left invariant as a whole.
- Glide reflection. A glide reflection is an isometry of the second kind as well. It can be conceived as a combination of a reflection in a plane and a translation parallel to this plane. The mirror plane of the reflection is now called a glide plane. The translation vector of the translation involved is called the glide vector g. There is no fixed point of a glide reflection. Left invariant as a whole are the glide plane and those planes which are perpendicular to the glide plane and parallel to g as well as those lines of the glide plane which are parallel to g.
Crystallographic site-symmetry operations
In theoretical and practical work one frequently needs to know the symmetry around a position in a molecule or in a crystal structure. The symmetry of the surroundings of an atom or of the center of gravity of a (more or less complex) group of atoms (ion, molecule, etc.) is determined, among others, by chemical bonds. The surroundings of such a constituent strongly influence the physical and chemical properties of a substance. A striking example is the pair 'graphite and diamond', which both are chemically carbon but display different surroundings of the carbon atoms and thus extremely different chemical and physical properties.
The symmetry of the surroundings of a point ![]() , called the site symmetry or point symmetry of
, called the site symmetry or point symmetry of ![]() , is determined by the symmetry of the whole molecule or crystal and by the locus of
, is determined by the symmetry of the whole molecule or crystal and by the locus of ![]() in the molecule or crystal. Here, we are interested in crystallographic site symmetries only, i.e. the local symmetries around points
in the molecule or crystal. Here, we are interested in crystallographic site symmetries only, i.e. the local symmetries around points ![]() in a crystal (better, in a crystal pattern). Strictly, one defines:
in a crystal (better, in a crystal pattern). Strictly, one defines:
Definition (D 3.2.2) The set ![]() of all symmetry operations of a crystal pattern is called the space group of the crystal pattern. The set of all elements of
of all symmetry operations of a crystal pattern is called the space group of the crystal pattern. The set of all elements of ![]() , i.e. of the space group, which leave a given point
, i.e. of the space group, which leave a given point ![]() fixed, is called the site symmetry, site-symmetry group, point-symmetry group, or point group
fixed, is called the site symmetry, site-symmetry group, point-symmetry group, or point group ![]() of
of ![]() with regard to the space group
with regard to the space group ![]() .
.
In this manuscript the term site-symmetry group or, for short, site symmetry, is preferred for reasons which will become clear in Section 3.4.
Because of its periodicity each crystal has an infinite number of translations as symmetry operations, i.e. ![]() is an infinite set. However, a translation can not be an element of a site-symmetry group because a translation has no fixed point at all. The same holds for screw rotations and glide reflections.
is an infinite set. However, a translation can not be an element of a site-symmetry group because a translation has no fixed point at all. The same holds for screw rotations and glide reflections.
For the description of the crystallographic symmetry operations, it is convenient to have available the notion of the 'order of an isometry'.
Definition (D 3.2.2) An isometry W has the (or: is of) order ![]() , if
, if ![]() holds, where
holds, where ![]() is the identity operation, and
is the identity operation, and ![]() is the smallest number, for which this equation is fulfilled.
is the smallest number, for which this equation is fulfilled.
Remark. The ![]() different isometries
different isometries ![]() ,
, ![]() = 1, ...,
= 1, ..., ![]() , form a group with
, form a group with ![]() elements. See also the definition (D 3.4.2) of the group order.
elements. See also the definition (D 3.4.2) of the group order.
The following types of isometries may be elements of crystallographic site symmetries:
- Identity. The identity I is a member of any crystallographic site-symmetry group because it leaves any point fixed. It is the only operation whose order is 1, its Hermann-Mauguin symbol (HM symbol) is also 1. [The
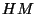 symbols have been introduced by CARL HERMANN and CHARLES MAUGUIN around 1930. There are
symbols have been introduced by CARL HERMANN and CHARLES MAUGUIN around 1930. There are 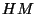 symbols for point-group and for space-group operations, as well as for site-symmetry, space, and point groups. In IT A the
symbols for point-group and for space-group operations, as well as for site-symmetry, space, and point groups. In IT A the 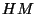 symbols form the standard nomenclature].
symbols form the standard nomenclature]. - Inversion. If the inversion is a member of the site-symmetry group, then the point
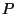 is the center of inversion. The order of the inversion is 2, its
is the center of inversion. The order of the inversion is 2, its 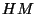 symbol is
symbol is 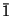 .
. -
Rotations. The point
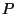 is placed on the rotation axis. Due to the periodicity of the crystals, the rotation angles of crystallographic rotations are restricted to multiples of
is placed on the rotation axis. Due to the periodicity of the crystals, the rotation angles of crystallographic rotations are restricted to multiples of 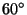 and
and 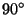 , i.e. to
, i.e. to 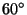 ,
, 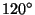 ,
, 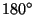 ,
, 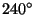 ,
, 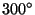 ,
, 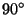 , and
, and 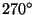 . All these angles are of the form
. All these angles are of the form 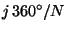 , where
, where 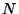 =2, 3, 4, or 6, and
=2, 3, 4, or 6, and 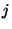 is an integer which is relative prime to
is an integer which is relative prime to 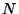 . (This restriction does not hold for the symmetry of molecules which may display, e.g., a rotation angle of
. (This restriction does not hold for the symmetry of molecules which may display, e.g., a rotation angle of 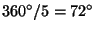 and its multiples.) Moreover, the angles between different axes of crystallographic rotations are limited to a small number of values only.
and its multiples.) Moreover, the angles between different axes of crystallographic rotations are limited to a small number of values only.
A rotation with the rotation angle
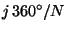 is called an
is called an 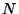 -fold rotation. Its
-fold rotation. Its  symbol is
symbol is 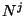 . The
. The 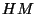 symbols of the crystallographic rotations are
symbols of the crystallographic rotations are 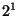 = 2
= 2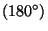 ,
, 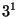 =3
=3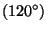 ,
, 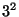 =
=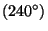 ,
, 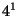 =4
=4 ,
, 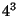 =
= ,
, 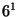 =
=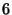
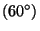 ,
, 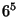 =
=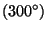 , (and 1
, (and 1 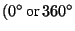 ) for the identity). The order of the rotation
) for the identity). The order of the rotation 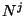 is
is 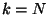 .
. -
Rotoinversions. The point
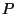 is placed in the inversion point on the rotoinversion axis. The restrictions on the angles
is placed in the inversion point on the rotoinversion axis. The restrictions on the angles 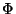 of the rotational parts are the same as for rotations. If
of the rotational parts are the same as for rotations. If 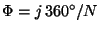 , the rotoinversion is called an
, the rotoinversion is called an 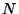 -fold rotoinversion. The
-fold rotoinversion. The 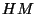 symbol for such a rotoinversion is
symbol for such a rotoinversion is 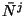 . In crystals can occur:
. In crystals can occur:
(
 inversion),
inversion), 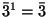 ,
, 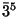 ,
, 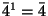 ,
, 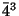 ,
, 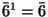 , and
, and 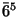 . The rotoinversion
. The rotoinversion 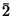 is identical with a reflection, see next item.
is identical with a reflection, see next item.Question. Which isometry is
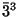 ,
, 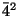 ,
, 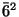 , and
, and 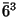 ? The answer to this question is found at the end of this chapter.
? The answer to this question is found at the end of this chapter. - Reflections. The point
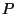 is situated on the mirror plane. There are only a few possible angles between the normals of different mirror planes belonging to the reflections of a site-symmetry group:
is situated on the mirror plane. There are only a few possible angles between the normals of different mirror planes belonging to the reflections of a site-symmetry group: 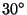 ,
, 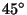 ,
, 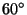 , and
, and 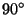 . The
. The  symbol of a reflection is
symbol of a reflection is 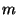 (mirror, miroir) instead of
(mirror, miroir) instead of  . The order of a reflection is 2, because its 2-fold application yields the identity operation.
. The order of a reflection is 2, because its 2-fold application yields the identity operation.
Space-group operations
The following facts are stated, their proof is beyond the scope of this manuscript:
- The symmetry operations listed in Section 3.2 are elements of space groups which leave the given point
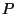 fixed, see definition (D 3.2.1). Therefore, identity, inversion, rotations, rotoinversions, and reflections are symmetry operations of space groups. Moreover, the same restrictions for the possible angles of rotation and rotoinversion of space-group operations hold as in Section 3.2. This concerns also the rotations involved in screw rotations.
fixed, see definition (D 3.2.1). Therefore, identity, inversion, rotations, rotoinversions, and reflections are symmetry operations of space groups. Moreover, the same restrictions for the possible angles of rotation and rotoinversion of space-group operations hold as in Section 3.2. This concerns also the rotations involved in screw rotations. - It is always possible to choose a primitive basis, see definition (D 1.5.2) and the remarks to it. Referred to a primitive basis, all lattice vectors of the crystal are integer linear combinations of the basis vectors. Each of these lattice vectors defines a (symmetry) translation. The order of any translation T is infinite because there is no number
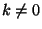 such that
such that 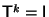 .
. - Parallel to each rotation, screw-rotation, or rotoinversion axis as well as parallel to the normal of each mirror or glide plane there is a row of lattice vectors.
- Perpendicular to each rotation, screw-rotation, or rotoinversion axis as well as parallel to each mirror or glide plane there is a plane of lattice vectors.
- Let
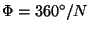 be the rotation angle of a screw rotation, then the screw rotation is called
be the rotation angle of a screw rotation, then the screw rotation is called 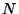 -fold. Note that the order of any screw rotation is infinite. Let u be the shortest lattice vector in the direction of the corresponding screw axis, and
-fold. Note that the order of any screw rotation is infinite. Let u be the shortest lattice vector in the direction of the corresponding screw axis, and 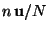 , with
, with 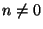 and integer, be the screw vector of the screw rotation by the angle
and integer, be the screw vector of the screw rotation by the angle  . Then the
. Then the  symbol of the screw rotation is
symbol of the screw rotation is 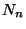 .
.
Performing an
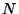 -fold rotation
-fold rotation 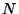 -times results in the identity mapping, i.e. the crystal has returned to its original position. After
-times results in the identity mapping, i.e. the crystal has returned to its original position. After 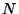 screw rotations with rotation angle
screw rotations with rotation angle 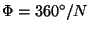 the crystal has its original orientation but is shifted parallel to the screw axis by the lattice vector
the crystal has its original orientation but is shifted parallel to the screw axis by the lattice vector 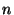 u.
u. - Let W be a glide reflection. Then the glide vector is parallel to the glide plane and is 1/2 of a lattice vector t. Whereas twice the application of a reflection restores the original position of the crystal, applying a glide reflection twice results in a translation of the crystal with the translation vector t. The order of any glide reflection is infinite. The
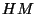 symbol of a glide reflection is
symbol of a glide reflection is 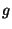 in the plane and
in the plane and 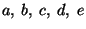 , or
, or 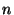 in the space. The letter indicates the direction of the glide vector g relative to the basis of the coordinate system.
in the space. The letter indicates the direction of the glide vector g relative to the basis of the coordinate system.
Crystallographic groups
The symmetry, i.e. the set of all symmetry operations, of any object forms a group in the mathematical sense of the word. Therefore, the theorems and results of group theory can be used when dealing with the symmetries of crystals. The methods of group theory can not be treated here but a few results of group theory for crystallographic groups will be stated and used.
We start with the definition of the terms 'subgroup' and 'order of a group'.
Definition (D 3.4.3) Let ![]() and
and ![]() be groups such that all elements of
be groups such that all elements of ![]() are also elements of
are also elements of ![]() . Then
. Then ![]() is called a subgroup of
is called a subgroup of ![]() .
.
Remark. According to its definition, each crystallographic site-symmetry group is a subgroup of that space group from which its elements are selected.
Definition (D 3.4.3) The number ![]() of elements of a group
of elements of a group ![]() is called the order of
is called the order of ![]() . In case
. In case ![]() exists,
exists, ![]() is called a finite group. If there is no (finite) number
is called a finite group. If there is no (finite) number ![]() ,
, ![]() is called an infinite group.
is called an infinite group.
Remark. The term 'order' is an old mathematical term and has nothing to do with order or disorder in crystals. Space groups are always infinite groups; crystallographic site-symmetry groups are always finite.
The following results for crystallographic site-symmetry groups ![]() and point groups
and point groups ![]() are known for more than 170, those for space groups
are known for more than 170, those for space groups ![]() more than 100 years.
more than 100 years.
We consider site-symmetry groups first.
- The possible crystallographic site-symmetry groups
 are always finite groups. The maximal number of elements of
are always finite groups. The maximal number of elements of  in the plane is 12, in the space is 48.
in the plane is 12, in the space is 48. - Due to the periodicity of the crystal, crystallographic site-symmetry groups never occur singly. Let
 be the site-symmetry group of a point
be the site-symmetry group of a point 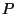 , and
, and 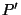 be a point which is equivalent to
be a point which is equivalent to 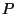 under a translation of
under a translation of  . To
. To  belongs a site-symmetry group
belongs a site-symmetry group  which is equivalent to
which is equivalent to  . The infinite number of translations results in an infinite number of points
. The infinite number of translations results in an infinite number of points  and thus in an infinite number of groups
and thus in an infinite number of groups  which all are equivalent to
which all are equivalent to  . In Subsection 5.3.1 is shown, how
. In Subsection 5.3.1 is shown, how  can be calculated from
can be calculated from 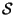 .
.
Note that this assertion is correct even if not all of the groups
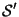 are different. This is demonstrated by the following example: If the site symmetry
are different. This is demonstrated by the following example: If the site symmetry 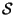 of
of 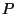 consists of a reflection and the identity, the point
consists of a reflection and the identity, the point 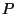 is placed on a mirror plane. If the translation mapping
is placed on a mirror plane. If the translation mapping 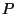 onto
onto 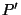 is parallel to this plane, then
is parallel to this plane, then  of
of 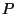 and
and 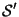 of
of 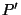 are identical. Nevertheless, there are always translations of
are identical. Nevertheless, there are always translations of 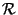 which are not parallel to the mirror plane and which carry
which are not parallel to the mirror plane and which carry 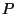 and
and 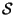 to points
to points 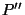 with site symmetries
with site symmetries 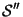 . These are different from but equivalent to
. These are different from but equivalent to  . The groups
. The groups  and
and  leave different planes invariant.
leave different planes invariant. - According to their geometric meaning the groups
 may be classified into types. A type of site-symmetry groups is also called a crystal class.
may be classified into types. A type of site-symmetry groups is also called a crystal class. - There are altogether 10 crystal classes of the plane. Geometrically, their groups are the symmetries of the regular hexagon, of the square, and the subgroups of these symmetries. Within the same crystal class, the site-symmetry groups consist of the same number of rotations and reflections and have thus the same group order. The rotations have the same rotation angles. Site-symmetry groups of different crystal classes differ by the number and angles of their rotations and/or by the number of their reflections and often by their group orders.
- There are 32 crystal classes of groups
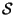 of the space. Their groups are the symmetries of the cube, of the hexagonal bipyramid, and the subgroups of these symmetries. Again, the groups
of the space. Their groups are the symmetries of the cube, of the hexagonal bipyramid, and the subgroups of these symmetries. Again, the groups  of the same crystal class agree in the numbers and kinds of their rotations, rotoinversions, reflections, and thus in the group orders. Moreover, there are strong restrictions for the possible relative orientations of the rotation and rotoinversion axes and of the mirror planes. Site-symmetry groups of different crystal classes differ by the numbers and kinds of their symmetry operations.
of the same crystal class agree in the numbers and kinds of their rotations, rotoinversions, reflections, and thus in the group orders. Moreover, there are strong restrictions for the possible relative orientations of the rotation and rotoinversion axes and of the mirror planes. Site-symmetry groups of different crystal classes differ by the numbers and kinds of their symmetry operations. - In order to get a better overview, the crystal classes are further classified into crystal systems and crystal families.
The following exercise deals with a simple example of a possible planar crystallographic site-symmetry group.
Problem 1A. Symmetry of the square.
 |
Questions For further questions, see Problem 1B, p. ![[*]](crossref.gif) .
.
- (i)
- List the symmetry operations of the square.
- (ii)
- What is the geometric meaning of each of these symmetry
operations ? - (iii)
- What are the orders of these symmetry operations ?
- (iv)
- How many symmetry operations of the square do exist ?
Some remarks on space groups follow.
Space groups are the symmetries of crystal patterns, they have been defined already by definition (D 3.2.1). Their order is always infinite because of the infinitely many translations. Not only the order but also the number of space groups is infinite because each existing or conceivable crystal (crystal pattern) has 'its' space group. However, an infinite set, as that of all space groups, is difficult to overlook. Therefore, it is advantageous to have a classification of the space groups into a finite number of classes.
The classification of site symmetries into types of site symmetries (crystal classes) has already been discussed. Like site-symmetry groups, also space groups may be classified into types, the space-group types. This classification into 230 space-group types is so commonly used that these space-group types are just called the 230 space groups in many text books and in the spoken language. In most cases there is no harm caused by this usage. However, for certain kinds of problems in crystal chemistry, or when dealing with phase transitions, the distinction between the individual 'space group' and the set 'type of space groups' is indispensable. The distinction is important enough to be illustrated by an example from daily life:
There are millions of cars running on earth but there are only a few hundred types of cars. One loosely says: 'I have the same car as my neighbour' when one means 'My car is of the same type as that of my neighbour'. The difference becomes obvious if the neighbour's car is involved in a traffic accident.
Really, there are 2 classifications of space groups into types. The one just mentioned may be called the 'classification into the 230 crystallographic space-group types'. The different types are distinguished by the occurence of different types of rotations, screw rotations, etc. (One can not argue with the 'numbers of 2-fold rotations' etc. because in space groups all these numbers are infinite). However, there are 11 pairs of these types, called enantiomorphic pairs, where in each pair the space groups of the one type can be transferred to those of the other type by improper but not by proper mappings. (Proper and improper mappings are defined in analogy to the proper and improper isometries, see Section 3.1. A pair of enantiomorphic space-group types is analogous to a pair of gloves: right and left). Counting each of these pairs as one type results in altogether 219 affine space-group types.
More than 2/3 of the 878 pp. of Vol. IT A, 4th edition (1995) are devoted to the description of the 17 'plane groups' and the 230 'space groups' (really: plane-group and space-group types). There are 4 ways for this description; 2 of them are described in the next section, the others in Sections 4.6 and 5.2.
The term point-symmetry group, point group, or point symmetry ![]() is used in 2 different meanings. In order to have a clear distinction between the 2 items which are commonly called 'point symmetry', the one item has been called 'site-symmetry group'
is used in 2 different meanings. In order to have a clear distinction between the 2 items which are commonly called 'point symmetry', the one item has been called 'site-symmetry group' ![]() or 'site symmetry', see above. This is done also in IT A, Section 8, 'Introduction to space-group theory'. The other item is the external symmetry
or 'site symmetry', see above. This is done also in IT A, Section 8, 'Introduction to space-group theory'. The other item is the external symmetry ![]() of the ideal macroscopic crystal. It is simultaneously the symmetry of its physical properties. The symmetry
of the ideal macroscopic crystal. It is simultaneously the symmetry of its physical properties. The symmetry ![]() is very much related to the symmetry
is very much related to the symmetry ![]() in so far as to each group
in so far as to each group ![]() there exists a group
there exists a group ![]() with the same order, the same number and kind of rotations, rotoreflections, and reflections, although not necessarily in the same space group. Analogously, to each group
with the same order, the same number and kind of rotations, rotoreflections, and reflections, although not necessarily in the same space group. Analogously, to each group ![]() there may exist groups
there may exist groups ![]() which have the same 'structure' as
which have the same 'structure' as ![]() has. Taken as groups without paying attention to the kind of operations,
has. Taken as groups without paying attention to the kind of operations, ![]() and
and ![]() cannot be distinguished. Therefore, the statements 1. to 6., made above for groups
cannot be distinguished. Therefore, the statements 1. to 6., made above for groups ![]() , are valid for groups
, are valid for groups ![]() as well, with the exception of statement 2. The latter is obvious: A macroscopic crystal is not periodic but 'a massive block' of finite extension, and there is only one finite symmetry group
as well, with the exception of statement 2. The latter is obvious: A macroscopic crystal is not periodic but 'a massive block' of finite extension, and there is only one finite symmetry group ![]() for the external shape of the crystal as compared to the infinite number of site-symmetry groups
for the external shape of the crystal as compared to the infinite number of site-symmetry groups ![]() .
.
What is the essential difference between ![]() and
and ![]() ? Why can they not be identified ?
? Why can they not be identified ?
The description of the symmetry ![]() is different from that of
is different from that of ![]() . The relation between
. The relation between ![]() and the space group
and the space group ![]() is simple:
is simple: ![]() is a subgroup of
is a subgroup of ![]() . The relation between
. The relation between ![]() and
and ![]() is more complicated and rather different. This will become clear from the following example.
is more complicated and rather different. This will become clear from the following example.
Example. There are not many compounds known whose symmetry consists of the identity, translations, and 2-fold rotations. The symbol of their space groups ![]() is
is ![]() . Several omphacites (rock-forming pyroxene minerals), high-temperature Nb
. Several omphacites (rock-forming pyroxene minerals), high-temperature Nb![]() O
O![]() , Cu
, Cu![]() In
In![]() O
O![]() , and a few more compounds are reported to belong to space-group type
, and a few more compounds are reported to belong to space-group type ![]() .
.
The compound Li![]() SO
SO![]() H
H![]() O is the best pyroelectric non-ferroelectric substance which is known today. Its space group
O is the best pyroelectric non-ferroelectric substance which is known today. Its space group ![]() is
is ![]() with the identity, translations, and 2-fold screw rotations
with the identity, translations, and 2-fold screw rotations ![]() . There are many compounds, e.g. sugars, with the same kinds of symmetry operations.
. There are many compounds, e.g. sugars, with the same kinds of symmetry operations.
Consider the points of point space. With regard to space group ![]() , there are points with site symmetry 2, namely all points situated on one of the 2-fold rotation axes. However, with regard to space group
, there are points with site symmetry 2, namely all points situated on one of the 2-fold rotation axes. However, with regard to space group ![]() there is no point with site symmetry 2, because screw rotations have no fixed points. Nevertheless, the symmetry of the macroscopic crystal is that of (identity and) a 2-fold rotation in both cases. One can say, that
there is no point with site symmetry 2, because screw rotations have no fixed points. Nevertheless, the symmetry of the macroscopic crystal is that of (identity and) a 2-fold rotation in both cases. One can say, that ![]() and
and ![]() have point groups of the same type, but exhibit strong differences in their site-symmetry groups.
have point groups of the same type, but exhibit strong differences in their site-symmetry groups.
In order to understand this difference it is useful to consider the determination of ![]() . A natural crystal is mostly distorted: the growth velocities of its faces have been influenced by currents of the medium from which the crystal has grown (liquid, gas), or by obstacles which have prevented the development of the ideal shape. Therefore, the faces present at a macroscopic crystal are replaced by their face normals for the determination of the macroscopic symmetry. These face normals are vectors which are independent of the state of development of the faces. Then
. A natural crystal is mostly distorted: the growth velocities of its faces have been influenced by currents of the medium from which the crystal has grown (liquid, gas), or by obstacles which have prevented the development of the ideal shape. Therefore, the faces present at a macroscopic crystal are replaced by their face normals for the determination of the macroscopic symmetry. These face normals are vectors which are independent of the state of development of the faces. Then ![]() is determined from the symmetry operations which map the bundle of face-normal vectors onto itself. Thus, the group
is determined from the symmetry operations which map the bundle of face-normal vectors onto itself. Thus, the group ![]() is a group of symmetry in vector space.
is a group of symmetry in vector space.
It is the conceptual difference between vector space and point space, experienced already in Section 1.4 when considering origin shifts, which leads to the difference between the groups ![]() and
and ![]() . The symmetry operations of
. The symmetry operations of ![]() are mappings of point space, whereas the symmetry operations of
are mappings of point space, whereas the symmetry operations of ![]() are mappings of vector space. In Section 4.4 the description of these operations by matrices will be dealt with. It will turn out that the difference between
are mappings of vector space. In Section 4.4 the description of these operations by matrices will be dealt with. It will turn out that the difference between ![]() and
and ![]() is reflected in the kinds of matrices which describe the operations of
is reflected in the kinds of matrices which describe the operations of ![]() and
and ![]() .
.
The above example of the space groups ![]() and
and ![]() has shown that there are space groups for which the groups
has shown that there are space groups for which the groups ![]() and
and ![]() may have the same order, namely in
may have the same order, namely in ![]() . This is a special property which deserves a separate name.
. This is a special property which deserves a separate name.
Definition (D 3.4.3) A space group is called symmorphic if there are site-symmetry groups ![]() which have the same order as the point group
which have the same order as the point group ![]() of the space group.
of the space group.
In the non-symmorphic space group ![]() , there is no group
, there is no group ![]() with the order 2 of
with the order 2 of ![]() .
.
Display of crystallographic symmetry in IT A
A crystallographic symmetry operation may be visualized geometrically by its 'geometric element', mostly called symmetry element. The symmetry element is a point, line, or plane related to the symmetry: depending on the symmetry operation, it is the center of inversion or (for rotoinversions) the inversion point; the rotation, screw rotation, or rotoinversion axis; the mirror or glide plane. Only the identity operation I and the translations T do not define a symmetry element. Whereas the symmetry element of a symmetry operation is uniquely defined, more than one symmetry operation may belong to a symmetry element. For example, to a 4-fold rotation axis belong the symmetry operations ![]() , and
, and ![]() around this axis.
around this axis.
[There is some confusion concerning the terms symmetry element and symmetry operation. It is caused by the fact that symmetry operations are the group elements of the symmetry groups (space groups, site-symmetry groups, or point groups). Symmetry operations can be combined resulting in other symmetry operations and forming a symmetry group. Symmetry elements can not be combined such that the combination results in a uniquely determined other symmetry element. As a consequence, symmetry elements do not form groups, and group theory can not be applied to them. Nevertheless, the description of symmetry by symmetry elements is very useful, as will be seen now.]
In IT A, crystallographic symmetry is described in 4 ways:
- The analytical description of symmetry operations by matrix-column pairs will be considered in Chapter 4. The listing of these matrix-column pairs as the 'General position' of IT A in a kind of short-hand notation will be discussed in Section 4.6.
- The geometric meaning of the matrix-column pair can be determined, see Section 5.2. In order to save the user this determination, in IT A the geometric meaning is listed for each matrix-column pair, see Section 4.6.
- A visual geometric description of a space group (more exactly: a space-group type) is possible by displaying the framework of symmetry elements in a diagram, see this section.
- In another diagram the space-group symmetry is represented by a set of points which are symmetrically equivalent under the operations of the space group, see this section.
In IT A, for each space group there are at least 2 diagrams displaying the symmetry (there are more diagrams for space groups of low symmetry). In this section only one example for each kind of diagrams can be discussed in order to explain the principles of this way of symmetry description. A full explanation of the details is found in IT A, Section 2.6 'Space-group diagrams', dto. in the Brief Teaching Edition of IT A.
The Figs. 3.5.1 and 3.5.2 are taken from IT A, space-group table No. 86, ![]() (
(![]() symbol for this space-group type),
symbol for this space-group type), ![]() (SCHOENFLIES symbol for this space-group type). In both diagrams, displayed is an orthogonal projection of a unit cell of the crystal onto the paper plane. The direction of projection is the c axis, the paper plane is the projection of the a-b plane (if c is perpendicular to a and b, then the paper plane is the a-b plane). The thin lines outlining the projection are the traces of the side planes of the unit cell. Because opposite lines represent translationally equivalent side planes of the unit cell, the line pairs can be considered as representing the basic translations a and b. The origin (projection of all points with coordinates 00
(SCHOENFLIES symbol for this space-group type). In both diagrams, displayed is an orthogonal projection of a unit cell of the crystal onto the paper plane. The direction of projection is the c axis, the paper plane is the projection of the a-b plane (if c is perpendicular to a and b, then the paper plane is the a-b plane). The thin lines outlining the projection are the traces of the side planes of the unit cell. Because opposite lines represent translationally equivalent side planes of the unit cell, the line pairs can be considered as representing the basic translations a and b. The origin (projection of all points with coordinates 00![]() ) is placed in the upper left corner; the other vertices represent the edges 10
) is placed in the upper left corner; the other vertices represent the edges 10![]() (lower left), 01
(lower left), 01![]() (upper right), and 11
(upper right), and 11![]() (lower right).
(lower right).
The following diagram is always placed on the left side of the page in IT A.
 |
| Fig. 3.5.1 Symmetry elements. A small circle represents a center of inversion |
In the unit cell or on its borders are (only 1 representative of each set of translationally equivalent elements is listed):
- (i)
- centers of inversion in 1/4,1/4,1/4; 1/4,1/4,3/4; 3/4,1/4,1/4;
3/4,1/4,3/4; 1/4,3/4,1/4; 1/4,3/4,3/4; 3/4,3/4,1/4; 3/4,3/4,3/4; - (ii)
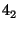 axes in 1/2,0,
axes in 1/2,0,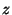 ; 0,1/2,
; 0,1/2,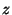 ;
;- (iii)
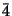 axes in 0,0,
axes in 0,0,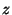 ; 1/2,1/2,
; 1/2,1/2,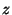 with inversion points in 0,0,0; 0,0,1/2; 1/2,1/2,0; 1/2,1/2,1/2;
with inversion points in 0,0,0; 0,0,1/2; 1/2,1/2,0; 1/2,1/2,1/2;- (iv)
- glide planes
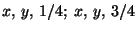 with glide vector 1/2,1/2,0.
with glide vector 1/2,1/2,0.
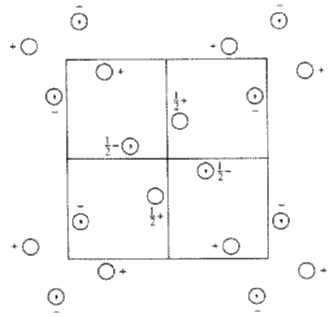 |
A '-sign (comma) in the circle means that this point is an image of the starting point by a symmetry operation of the second kind, see Section 3.1. If the empty circles are assumed to represent right gloves, then the circles with a comma represent left gloves, and vice versa.
The correspondence between the 2 diagrams is obvious: With some practice each of the diagrams can be produced from the other. Therefore, they are completely equivalent descriptions of the same space-group symmetry. Nevertheless, both diagrams are displayed in IT A in order to provide different aspects of the same symmetry. Because of the periodicity of the arrangement, the presentation of the contents of one unit cell is sufficient.
Answer to the question in Section 3.2.
![]() , (
, (![]() );
); ![]() ;
; ![]() ; and
; and ![]() , where the normal of the mirror plane is parallel to the rotoinversion axis of
, where the normal of the mirror plane is parallel to the rotoinversion axis of ![]() (the mirror plane itself is perpendicular to the rotoinversion axis).
(the mirror plane itself is perpendicular to the rotoinversion axis).
The following statements hold always:
The description of mappings by matrix-column pairs
Matrix-column pairs
As was mentioned already in Section 2.2, an affine mapping A is described by a matrix A and a column a, see equations (2.2.1) and (2.2.5) on p. ![[*]](crossref.gif) . Crystallographic symmetry operations are special affine mappings. They will be designated by the letter W and described by the matrix W and the column w. Their description is analogous to equation (2.2.1):
. Crystallographic symmetry operations are special affine mappings. They will be designated by the letter W and described by the matrix W and the column w. Their description is analogous to equation (2.2.1):
There are different ways of simplifying this array. One of them leads to the description with ![]() sign and indices in analogy to that for mappings, see equations (2.4.1) and (2.4.2). It will not be followed here. Another one is the symbolic description introduced in Section 2.3. It will be treated now in more detail.
sign and indices in analogy to that for mappings, see equations (2.4.1) and (2.4.2). It will not be followed here. Another one is the symbolic description introduced in Section 2.3. It will be treated now in more detail.
Step 1 One writes the system of equations in the form
The form 4.1.2 has the advantage that the coordinates and the coefficients which describe the mapping are no longer intimately mixed but are more separated in the equation. For actual calculations with concrete mappings this form is most appropriate, applying the definitions (D 2.4.3) and (D 2.4.2). For the derivation of general formulae, a further abstraction is advantageous.
Step 2 Denoting the coordinate columns by ![]() and x, the (
and x, the (![]() ) matrix by W, and the column by w, one obtains in analogy to equation (2.2.5)
) matrix by W, and the column by w, one obtains in analogy to equation (2.2.5)
Step 3 Still the coordinate part and the mapping part are not completely separated. Therefore, one writes
The latter form is called the SEITZ notation.Note that the forms (4.1.1) to (4.1.4) of the equations are only different ways of describing the same mapping W. The matrix-column pairs (W,w) or (W![]() w) are suitable in particular for general considerations; they present the pure description of the mapping, and the coordinates are completely eliminated. Therefore, in Section 4.2 the pairs are used for the formulation of the combination VU of 2 symmetry operations V and U and of the inverse W
w) are suitable in particular for general considerations; they present the pure description of the mapping, and the coordinates are completely eliminated. Therefore, in Section 4.2 the pairs are used for the formulation of the combination VU of 2 symmetry operations V and U and of the inverse W![]() of a symmetry operation W. However, if one wants to provide a list of specific mappings, then there is no way to avoid the explicit description by the formulae 4.1.1 or 4.1.2, see Section 4.6.
of a symmetry operation W. However, if one wants to provide a list of specific mappings, then there is no way to avoid the explicit description by the formulae 4.1.1 or 4.1.2, see Section 4.6.
With the matrix-column pairs one can replace geometric considerations by analytical calculations. To do this one first determines those matrix-column pairs which describe the symmetry operations to be studied. This will be done in Section 5.1. Then one performs the necessary procedures with the matrix-column pairs, e.g. combination or reversion, see Section 4.2. Finally, one has to extract the geometric meaning from the resulting matrix-column pairs. This last step is shown in Section 5.2.
Combination and reversion of mappings
The combination of 2 symmetry operations follows the procedure of Section 2.2. In analogy to equations (2.2.5) to (2.2.8) one obtains
These equations may be formulated with matrix-column pairs:
Note that in the product (V,v)(U,u) the operation (U,u) is performed first and (V,v) second. Because of writing point coordinates and vector coefficients as columns, in the combination of their mappings the sequence is always from right to left.By comparing equations (4.2.4) and (4.2.5) one obtains
This law of composition for matrix-column pairs is not easy to keep in mind because of its asymmetry. It would be easy if the resulting matrix part would be the product of the original matrices and the resulting column the sum of the original columns. However, the column u of the operation, which is applied to the pointThe multiplication of matrix-column pairs is associative, because
| (4.2.7) |
and on the other hand,
| (4.2.8) |
By comparison of both expressions one finds
Associativity is a very important property. It can be used, e.g., to find the value of a product of matrix-column pairs without any effort. Suppose, that in the above triple product of matrix-column pairs,A linear mapping is a mapping which leaves the origin fixed. Its column part is thus the o column. According to equation (4.2.6) any matrix-column pair can be decomposed into a linear mapping (W,o) containing W only and a translation (I,w) with w only:
Question: What is the result if the translation (I,w) is performed first, and the linear mapping (W,o) after that, i.e. if the factors are exchanged ?
Before the reversion of a symmetry operation is dealt with, a general remark is appropriate. In general, the formulae of this section are not restricted to crystallographic symmetry operations but are valid also for affine mappings. However, there is one exception. In the inversion of a matrix W the determinant ![]() appears in the denominator of the coefficients of
appears in the denominator of the coefficients of ![]() , see Subsection 2.6.1. Therefore, the condition
, see Subsection 2.6.1. Therefore, the condition ![]() has to be fulfilled. Such mappings are called regular or non-singular. Otherwise, if
has to be fulfilled. Such mappings are called regular or non-singular. Otherwise, if ![]() , the mapping is a projection and can not be reverted. For crystallographic symmetry operations, i.e. isometries W, always
, the mapping is a projection and can not be reverted. For crystallographic symmetry operations, i.e. isometries W, always ![]() holds. Therefore, an isometry is always reversible, a general affine mapping may not be. Projections are excluded from this manuscript because they do not occur in crystallographic groups.
holds. Therefore, an isometry is always reversible, a general affine mapping may not be. Projections are excluded from this manuscript because they do not occur in crystallographic groups.
Now to the calculation of the reverse of a matrix-column pair. It is often necessary to know which matrix C and column c belong to that symmetry operation C which makes the original action W undone, i.e. which maps every image point ![]() onto the original point
onto the original point ![]() . The operation C is called the reverse operation of W. The combination of W with C restores the original state and the combined action CW maps
. The operation C is called the reverse operation of W. The combination of W with C restores the original state and the combined action CW maps ![]() . It is the identity operation I which maps any point
. It is the identity operation I which maps any point ![]() onto itself. The operation I is described by the matrix-column pair (I,o), where I is the unit matrix and o is the column consisting of zeroes only. This means
onto itself. The operation I is described by the matrix-column pair (I,o), where I is the unit matrix and o is the column consisting of zeroes only. This means
It is always good to test the result of a calculation or derivation. One verifies the validity of the equations ![]() by applying equations (4.2.6) and (4.2.12). In addition in the following Problem 2A the results of this section may be practised.
by applying equations (4.2.6) and (4.2.12). In addition in the following Problem 2A the results of this section may be practised.
Problem 2A. Symmetry described by matrix-column pairs.
In Vol. A of International Tables for Crystallography the crystallographic symmetry operations A, B, ... are referred to a conventional coordinate system and are represented by matrix-column pairs (A,a), (B,b), .... Among others one finds in the space-group tables of IT A indirectly, see Section 4.6:
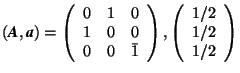 and
and 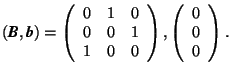
Combining two symmetry operations or reversion of a symmetry operation corresponds to multiplication or reversion of these matrix-column pairs, such that the resulting matrix-column pair represents the resulting symmetry operation.
The following calculations make use of the formulae 4.2.6 and 4.2.12.
Can one exploit the fact that the matrices A, B, C, and D are orthogonal matrices ?
Questions
- (i)
- What is the matrix-column pair resulting from
(B, b)(A, a) = (C,c) ? - (ii)
- What is the matrix-column pair resulting from
(A, a)(B, b) = (D,d) ? - (iii)
- What is (A,a)
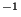 ?
? - (iv)
- What is (B,b)
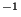 ?
? - (v)
- What is (C,c)
 ?
? - (vi)
- What is (D,d)
 ?
? - (vii)
- What is (B,b)
 (A, a)
(A, a) ?
?
![[*]](crossref.gif) .
.
(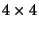 ) matrices
) matrices
The formulae (4.2.6) and (4.2.12) are difficult to keep in mind. It would be fine to have them in a more user-friendly shape. Such a shape exists and will be demonstrated now. It is not only more convenient but also solves another problem, viz the clear distinction between point coordinates and vector coefficients, as will be seen in Section 4.4.
If a crystallographic symmetry operation is described by the matrix-column pair (W,w), then one can form the ![]() matrix
matrix
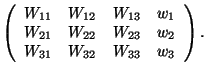 |
Regrettably, such matrices can not be multiplied with each other because of the different number (4) of columns of the left matrix and (3) of rows of the right matrix, see Section 2.4. However, one can make the matrix square by adding a fourth row '0 0 0 1'. Such ![]() matrices can be multiplied with each other. For the applications also the coordinate columns have to be extended. This is done by adding a fourth row with the number 1 to the
matrices can be multiplied with each other. For the applications also the coordinate columns have to be extended. This is done by adding a fourth row with the number 1 to the ![]() column. We thus have:
column. We thus have:
Definition (D 4.3.1) The ![]() matrix
matrix ![]() obtained from W and w in the way just described is called the augmented matrix
obtained from W and w in the way just described is called the augmented matrix ![]() ; the columns are called augmented columns.
; the columns are called augmented columns.
The horizontal and vertical lines in the matrix and the horizontal line in the columns have no mathematical meaning; they are to remind the user of the geometric contents and of the way in which the matrix has been built up.
Equation (4.1.2) is replaced by an equation in outlined letters
For the reverse mapping ![]() holds, where
holds, where ![]() is the (
is the (![]() ) unit matrix. This is fulfilled for
) unit matrix. This is fulfilled for
In practice the augmented quantities are very convenient for general formulae and for the actual combination of mappings by multiplying ![]() matrices. Equation (4.3.4) is useful to provide the inverse of a
matrices. Equation (4.3.4) is useful to provide the inverse of a ![]() matrix by calculating the right side. It does not make sense to invert a
matrix by calculating the right side. It does not make sense to invert a ![]() matrix using equation (2.6.1) on p.
matrix using equation (2.6.1) on p. ![[*]](crossref.gif) for direct matrix inversion.
for direct matrix inversion.
In an analogous way one can describe mappings of the plane by ![]() augmented matrices and
augmented matrices and ![]() augmented columns.
augmented columns.
Transformation of vector coefficients
It has already been demonstrated, in Section 1.4, that point coordinates and vector coefficients display a different behaviour when the coordinate origin is shifted. The same happens when a translation is applied to a pair of points. The coordinates of the points will be changed according to
However, the distance between the points will be invariant:
Distances are absolute values of vectors, see Section 1.6. Usually point coordinates and vector coefficients are described by the same kind of ![]() columns and are difficult to distinguish. It is a great advantage of the augmented columns to provide a clear distinction between these quantities.
columns and are difficult to distinguish. It is a great advantage of the augmented columns to provide a clear distinction between these quantities.
If ![]() and
and ![]() are the augmented columns of coordinates of the points
are the augmented columns of coordinates of the points ![]() and
and ![]() ,
,
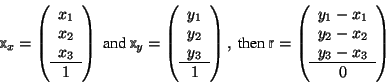
is the augmented column
Let T be a translation, (I,t) its matrix-column pair, ![]() its augmented matrix, r the
its augmented matrix, r the ![]() column of coefficients of the distance vector r between
column of coefficients of the distance vector r between ![]() and
and ![]() , and
, and ![]() the augmented column of r. Then,
the augmented column of r. Then,
When using augmented columns and matrices, the coefficients of t are multiplied with the last coefficient 0 of the ![]() column and thus become ineffective.
column and thus become ineffective.
This behaviour is valid not only for translations but holds in general for affine mappings, and thus for isometries and crystallographic symmetry operations:
Whereas point coordinates are transformed by ![]() , vector coefficients r are affected only by the matrix part W:
, vector coefficients r are affected only by the matrix part W:
Note that ![]() is different from
is different from ![]() . The latter expression describes the image point
. The latter expression describes the image point ![]() of the point
of the point ![]() with the coordinates
with the coordinates ![]() .
.
The matrix-column pairs of crystallographic symmetry operations
For general matrices, multiplication and inversion may be rather tedious manipulations. These are unavoidable if the geometry of the object is complicated and if there is no way to simplify it. In crystallography one is in a better situation. By definition crystals are periodic, and their periodicity is not that of the continuum but that of the lattice. Therefore, primitive bases for the lattices can always be found, see definition (D 1.5.2). As a consequence, the matrix-column pairs for the crystallographic symmetry operations are simple if an appropriate coordinate system has been chosen. The conventional coordinate systems as used in the space- and plane-group tables of IT A are chosen under this aspect.
The matrix parts shall be considered first.
Suppose, a primitive lattice basis has been chosen as the coordinate basis. We take from the last section that the mapping of vectors by a crystallographic symmetry operation W is described only by the matrix part W of the ![]() matrix
matrix ![]() . The image of a lattice vector under a symmetry operation must be a lattice vector, otherwise the lattice would not be mapped onto itself as a whole. Being referred to a primitive basis, all lattice vectors have integer coefficients. Therefore, the matrix parts W of the crystallographic symmetry operations must have integer coefficients, they are integer matrices.
. The image of a lattice vector under a symmetry operation must be a lattice vector, otherwise the lattice would not be mapped onto itself as a whole. Being referred to a primitive basis, all lattice vectors have integer coefficients. Therefore, the matrix parts W of the crystallographic symmetry operations must have integer coefficients, they are integer matrices.
On the other hand, a crystallographic symmetry operation W is an isometry. Therefore, referred to an orthonormal basis, the matrix is an orthogonal matrix, see Subsection 2.6.1, p. ![[*]](crossref.gif) . When leaving all distances invariant, also the volume is invariant. Analytically, this means
. When leaving all distances invariant, also the volume is invariant. Analytically, this means ![]() .
.
If a matrix is integer and orthogonal, then in each row and column there are exactly one entry ![]() and 2 zeroes. The matrix has thus 3 coefficients
and 2 zeroes. The matrix has thus 3 coefficients ![]() and 6 zeroes. How many
and 6 zeroes. How many ![]() matrices of this kind do exist ? There are 6 arrangements to distribute the non-zero coefficients among the positions of the matrix. In addition, there are 3 signs with
matrices of this kind do exist ? There are 6 arrangements to distribute the non-zero coefficients among the positions of the matrix. In addition, there are 3 signs with ![]() possibilities of distributing + and
possibilities of distributing + and ![]() . Altogether there are
. Altogether there are ![]() different orthogonal integer matrices.
different orthogonal integer matrices.
The matrix parts of crystallographic symmetry operations form groups which describe the point groups, see Sections 3.4 and 4.4. The highest order of a crystallographic point group is 48, and referred to the conventional basis this point group is described by the group of the 48 orthogonal integer matrices. It is the point group of copper, gold, rocksalt, fluorite, galena, garnet, spinel, and many other crystalline compounds. The symmetries of 24 other point groups are contained as subgroups in this highest symmetry, so that 25 of the 32 types of point groups (crystal classes) can be described by orthogonal integer matrices. The advantages of these matrices are:
- The product of 2 matrices is easily calculated because of the many zeroes; it is again an orthogonal integer matrix.
- Due to the orthogonality, the inverse of a matrix is the transpose matrix and does not need calculation.
- The determinant of a matrix, see equation 2.5.2, is the product of 3 coefficients
 , adjusted for the sign.
, adjusted for the sign.
What about the necessary bases ? The matrix part of an isometry is orthogonal if referred to an orthonormal basis; it may also be orthogonal if referred to another basis. The restrictions to the basis depend on the point group. For example, the matrices describing the identity mapping and the inversion are orthogonal in any basis, viz the unit matrix and the negative unit matrix. The conventional bases in crystallography are lattice bases (not orthonormal bases). They are mostly chosen such that the matrices are integer orthogonal matrices. As already mentioned, this is possible for 25 of the 32 crystal classes of point groups.
The matrix is even simpler, if it is a diagonal orthogonal matrix, i.e. a diagonal matrix with coefficients ![]() . There are
. There are ![]() such matrices, among them the unit matrix I and the inversion
such matrices, among them the unit matrix I and the inversion ![]() . If the symmetry of the crystal is low enough, all matrices are diagonal. There are 8 crystal classes (of the 25) permitting such a description. Crystals with this symmetry are also called optically biaxial crystals because of their optical properties (birefringence).
. If the symmetry of the crystal is low enough, all matrices are diagonal. There are 8 crystal classes (of the 25) permitting such a description. Crystals with this symmetry are also called optically biaxial crystals because of their optical properties (birefringence).
The point groups of the remaining 7 crystal classes can not be described by orthogonal integer matrices. Referred to a primitive basis, their matrices are integer, of course. However, this representation is not orthogonal. One can choose an orthonormal basis instead but then the matrices are no longer integer matrices. These point groups are hexagonal and belong to the hexagonal crystal family.
Only in crystal physics the non-integer orthogonal representation is used for hexagonal point groups, in crystallography the representation by integer matrices is preferred. One introduces the so-called hexagonal basis, referred to which the matrices consist of at least 5 zeroes and 4 coefficients ![]() . In the conventional settings of IT A, there occur up to 16 such matrices, the other up to 8 matrices are orthogonal integer matrices. Although not necessary, also trigonal point groups are mostly referred to the hexagonal basis, because this description is for many crystals more natural than the decription by integer orthogonal matrices.
. In the conventional settings of IT A, there occur up to 16 such matrices, the other up to 8 matrices are orthogonal integer matrices. Although not necessary, also trigonal point groups are mostly referred to the hexagonal basis, because this description is for many crystals more natural than the decription by integer orthogonal matrices.
The column parts will be discussed now.
Provided a conventional coordinate system is chosen, also the coefficients of the columns are simple. They are determined
- by the choice of the basis which, however, is more or less fixed already by the matrix considerations.
- by the origin choice. If the origin is chosen in a fixed point of a symmetry operation W, then w is the o column. Clearly, one choice of the origin is such that as many of the symmetry operations as possible have the origin as fixed point.
The 'General Position' in IT A
In IT A the set of all symmetry operations is listed for all space groups. As we have seen, space groups are infinite groups, and there is an infinite number of space groups for each space-group type, see Section 3.4. How can such a listing be done at all ? In this section the principles are dealt with which make the listings possible, as well as the points of view which determine the actual listings.- Consider the infinite number of space groups belonging to a certain space-group type. If one refers each space group to its conventional coordinate system, one obtains a set of matrix-column pairs for each space group but all these sets are identical. (This is one way to classify the space groups into space-group types.) Therefore, a listing is necessary only for each space-group type, but not for each space group. This means 230 listings for the space groups and 17 listings for the plane groups, and these listings are indeed contained in IT A. In reality the number of space-group listings is higher by about 20 % because there is sometimes more than one conventional coordinate system: different settings, different bases, or different origins, see IT A.
- No doubt, there is an infinite number of symmetry operations for each space group. How can they be listed in a book of finite volume ? Let W be a symmetry operation and (W,w) its matrix-column pair. Because the conventional bases are always lattice bases, (W,w) can be decomposed into a translation
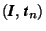 with integer coefficients and the matrix
with integer coefficients and the matrix 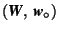 :
:
For the coefficients holds. By this decomposition one splits the infinite set of pairs (W,w) into a finite set of representatives
holds. By this decomposition one splits the infinite set of pairs (W,w) into a finite set of representatives  and an infinite set of translations
and an infinite set of translations 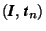 . Clearly, only the representatives need to be listed. Such a list is contained in IT A for each space-group type; the number of necessary entries is reduced from infinite to at most 48.
. Clearly, only the representatives need to be listed. Such a list is contained in IT A for each space-group type; the number of necessary entries is reduced from infinite to at most 48.
For primitive bases, the list is complete and unique. There are ambiguities for centered settings, see the remarks to definition (D 1.5.2). For example, for a space group with an
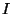 -centered lattice, to each point
-centered lattice, to each point 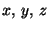 there belongs a translationally equivalent point
there belongs a translationally equivalent point 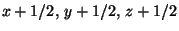 . Nevertheless, only one entry
. Nevertheless, only one entry 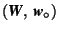 is listed. Again, instead of listing a translationally equivalent pair for each entry, the centering translation is extracted from the list and written once for all on top of the listing. For example, the rational translations for the
is listed. Again, instead of listing a translationally equivalent pair for each entry, the centering translation is extracted from the list and written once for all on top of the listing. For example, the rational translations for the 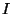 -centered lattice are indicated by '(0,0,0)+
-centered lattice are indicated by '(0,0,0)+ 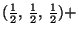 '. For each of the matrix-column pairs
'. For each of the matrix-column pairs 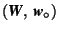 , listed in the sequel, not only the products
, listed in the sequel, not only the products 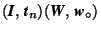 have to be taken into account, but also the products
have to be taken into account, but also the products 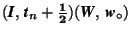 . (The term
. (The term 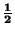 is a symbol for the column with all coefficients
is a symbol for the column with all coefficients 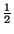 .) The following example 3 (General position for space-group type
.) The following example 3 (General position for space-group type 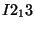 , No. 199) provides such a listing.
, No. 199) provides such a listing. - The representatives
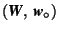 could be listed as matrix-column pairs but that would be wasting space. Although one could not save much space with further conventions when listing general matrices, the simple (48 orthogonal + 16 other = 64) standard matrices of crystallography with their many zeroes have a great potential for rationalization. Is there any point to list thousands of zeroes ? Therefore, in crystallography an efficient procedure is applied to condense the description of symmetry by matrix-column pairs considerably. This method works like the shorthand notation for the normal language, when the usual letters are replaced by shorthand symbols.
could be listed as matrix-column pairs but that would be wasting space. Although one could not save much space with further conventions when listing general matrices, the simple (48 orthogonal + 16 other = 64) standard matrices of crystallography with their many zeroes have a great potential for rationalization. Is there any point to list thousands of zeroes ? Therefore, in crystallography an efficient procedure is applied to condense the description of symmetry by matrix-column pairs considerably. This method works like the shorthand notation for the normal language, when the usual letters are replaced by shorthand symbols.
The equations (4.1.1) on p.
![[*]](crossref.gif) are shortened in the following way:
are shortened in the following way:- The left side and the '=' sign are omitted
- On the right side, all terms with coefficients 0 are omitted
- Coefficients '+1' are omitted, coefficients '-1' are replaced by '-' and are frequently written on top of the variable:
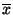 instead of
instead of 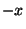 , etc.
, etc. - The three different rows are written in one line but separated by commas.
3 examples shall display the procedure.
Example 1. 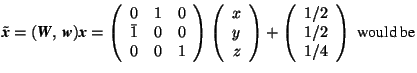
![]() .
.
The shorthand notation of IT A reads ![]() .
.
It is found in IT A under space group ![]() , No. 96 on p. 367. There it is entry (4) of the first block (the so-called General position) under the heading Positions.
, No. 96 on p. 367. There it is entry (4) of the first block (the so-called General position) under the heading Positions.
Example 2. 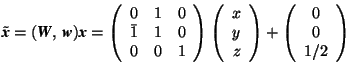
is written in the shorthand notation of IT A ![]() ; space group
; space group ![]() , No. 186 on p. 575 of IT A. It is entry (5) of the General position.
, No. 186 on p. 575 of IT A. It is entry (5) of the General position.
Example 3. The following table is the actual listing of the General position for space-group type ![]() , No. 199 in IT A on p. 603. The 12 entries, numbered (1) to (12), are to be taken as they are (indicated by (0,0,0)+) and in addition with 1/2 added to each element
, No. 199 in IT A on p. 603. The 12 entries, numbered (1) to (12), are to be taken as they are (indicated by (0,0,0)+) and in addition with 1/2 added to each element ![]() (indicated by
(indicated by ![]() . Altogether these are 24 entries, which is announced by the first number in the row, the 'Multiplicity'. The reader is recommended to convert some of the entries into matrix-column pairs or
. Altogether these are 24 entries, which is announced by the first number in the row, the 'Multiplicity'. The reader is recommended to convert some of the entries into matrix-column pairs or ![]() matrices.
matrices.
|
Positions
Multiplicity, |
Coordinates |
|
|
|
The listing of the 'General position' kills two birds with one stone:
- (i)
- each of the numbered entries lists the coordinates of an image point
 of the original point X under a symmetry operation of the space group.
of the original point X under a symmetry operation of the space group. - (ii)
- Each of the numbered entries of the General position lists a symmetry operation of the space group by the shorthand notation of the matrix-column pair. This fact is not as obvious as the meaning described under (i) but it is much more important. Knowing this way one can extract and make available for calculations the full analytical symmetry information of the space group from the tables of IT A.
Exactly one image point belongs to each of the infinitely many symmetry operations and vice versa. Some of these points are displayed in Figure 3.5.2 on p. ![[*]](crossref.gif) .
.
Definition (D 4.6.2) The set of all points which are symmetrically equivalent to a starting point ![]() (and thus to each other) under the symmetry operations of a space group
(and thus to each other) under the symmetry operations of a space group ![]() is called a point orbit
is called a point orbit ![]() of the space group.
of the space group.
Remarks.
- The starting point is a point of the orbit because it is mapped onto itself by the identity operation (I,o) which is a symmetry operation of any space group.
- The one-to-one correspondence between symmetry operations and points is valid only for the General position, i.e. the first block from top in the space-group tables. In this block the coordinate triplets (shorthand symbols for symmetry operations) refer to points which have site symmetry
 , i.e. only the identity operation is a symmetry operation. In all the other blocks, the points have site symmetries
, i.e. only the identity operation is a symmetry operation. In all the other blocks, the points have site symmetries 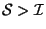 with more than one site-symmetry operation. If
with more than one site-symmetry operation. If 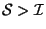 , also
, also 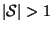 holds, where
holds, where 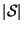 is the order of
is the order of 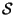 . One can show, that the point
. One can show, that the point 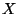 is mapped onto its image
is mapped onto its image 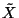 by exactly as many symmetry operations of the space group
by exactly as many symmetry operations of the space group 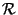 as is the order of the site-symmetry group
as is the order of the site-symmetry group 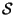 of
of 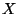 . Therefore, for such points the symmetry operation can not be derived from the data listed in IT A because it is not uniquely determined.
. Therefore, for such points the symmetry operation can not be derived from the data listed in IT A because it is not uniquely determined.
Different from the General position, a coordinate triplet of a special position provides the coordinates ![]() of the image point of the starting point
of the image point of the starting point ![]() only but no information on a matrix-column pair.
only but no information on a matrix-column pair.
Special aspects of the matrix formalism
The contents of this chapter serve two purposes:
- To forge a link between geometry and calculations;
- To provide the tools for coordinate changes.
The first point is described in the first two sections. The questions to be discussed are:
- (i)
- How can the matrix-column pair be obtained when the geometric meaning of the symmetry operation is known ?
- (ii)
- Given a matrix-column pair, what is its geometric meaning ?
The second point is a practical one. The complexity and amount of calculations depend strongly on the coordinate system of reference for the geometric actions. Therefore, it is advantageous to be flexible and free to choose for each calculation the optimal coordinate system. This means to change the coordinate system if necessary and to know what happens with the coordinates and the matrix-column pairs by such a change. In the last section of this chapter, partitioned into 3 subsections, coordinate changes will be treated in 3 steps: Origin shift, change of basis, and change of both, i.e. general coordinate changes.
Determination of the matrix-column pair
In this section it is assumed that not only the kind of symmetry operation is known but also its details, e.g. it is not enough to know that there is a 2-fold rotation, but one should also know the orientation and position of the rotation axis. At first one tries to find for some points ![]() their images
their images ![]() under the symmetry operation. This knowledge is then exploited to determine the matrix-column pair which decribes the symmetry operation.
under the symmetry operation. This knowledge is then exploited to determine the matrix-column pair which decribes the symmetry operation.
Examples will illustrate the procedures. In all of them the point coordinates are referred to a Cartesian coordinate system, see Section 1.2. The reader is recommended to make small sketches in order to see visually what happens.
In the system (4.1.1) of equations there are 12 coefficients to be determined, 9 ![]() and 3
and 3 ![]() . If the image point
. If the image point ![]() of one point
of one point ![]() is known from geometric considerations, one can write down the 3 linear equations of (4.1.1) for this pair of points. Therefore, writing down the equations (4.1.1) for 4 pairs (point
is known from geometric considerations, one can write down the 3 linear equations of (4.1.1) for this pair of points. Therefore, writing down the equations (4.1.1) for 4 pairs (point ![]() image point) is sufficient for the determination of all coefficients, provided the points are independent, i.e. are not lying in a plane. One obtains a system of 12 inhomogeneous linear equations with 12 undetermined parameters
image point) is sufficient for the determination of all coefficients, provided the points are independent, i.e. are not lying in a plane. One obtains a system of 12 inhomogeneous linear equations with 12 undetermined parameters ![]() and
and ![]() . This may be difficult to solve without a computer. However, if one restricts to crystallographic symmetry operations, the solution is easy more often than not because of the special form of the matrix-column pairs.
. This may be difficult to solve without a computer. However, if one restricts to crystallographic symmetry operations, the solution is easy more often than not because of the special form of the matrix-column pairs.
Procedure 1
In many cases it may be possible to apply the following strategy, which avoids all calculations. It requires knowledge of the image points of the origin ![]() and of the 3 'coordinate points'
and of the 3 'coordinate points' ![]() : 1,0,0;
: 1,0,0; ![]() : 0,1,0; and
: 0,1,0; and ![]() : 0,0,1.
: 0,0,1.
- (1)
- The origin Let
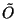 with coordinates
with coordinates 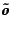 be the image of the origin
be the image of the origin  with coordinates o, i.e.
with coordinates o, i.e. 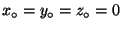 . Examination of the equations (4.1.1) shows that
. Examination of the equations (4.1.1) shows that 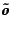 = w, i.e. the column w can be determined separately from the coefficients of the matrix W without any effort.
= w, i.e. the column w can be determined separately from the coefficients of the matrix W without any effort. - (2)
- The coordinate points We consider the point
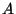 . Inserting 1,0,0 in the equations (4.1.1) one obtains
. Inserting 1,0,0 in the equations (4.1.1) one obtains 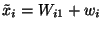 or
or 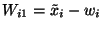 ,
,  The first column of W is separated from the others, and for the solution only the known coefficients
The first column of W is separated from the others, and for the solution only the known coefficients  have to be subtracted from the coordinates
have to be subtracted from the coordinates 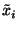 of the image point
of the image point 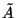 of
of 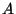 . Analogously one calculates the coefficients
. Analogously one calculates the coefficients 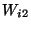 from the image of point
from the image of point 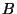 : 0,1,0 and
: 0,1,0 and 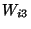 from the image of point
from the image of point  : 0,0,1.
: 0,0,1.
Example 1
What is the pair (W,w) for a glide reflection with the plane through the origin, the normal of the glide plane parallel to c, and with the glide vector g = 1/2,1/2,0 ?
- (a)
- Image of the origin
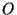 : The origin is left invariant by the reflection part of the mapping; it is shifted by the glide part to 1/2,1/2,0 which are the coordinates of
: The origin is left invariant by the reflection part of the mapping; it is shifted by the glide part to 1/2,1/2,0 which are the coordinates of  . Therefore, w = 1/2,1/2,0.
. Therefore, w = 1/2,1/2,0. - (b)
-
Images of the coordinate points. Both the points
 and
and  are not affected by the reflection part but
are not affected by the reflection part but  is then shifted to 3/2,1/2,0 and
is then shifted to 3/2,1/2,0 and 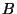 to 1/2,3/2,0. This results in the equations
to 1/2,3/2,0. This results in the equations
3/2 =
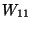 + 1/2, 1/2 =
+ 1/2, 1/2 = 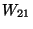 + 1/2, 0 =
+ 1/2, 0 = 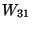 + 0 for
+ 0 for 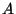 and
and1/2 =
 + 1/2, 3/2 =
+ 1/2, 3/2 = 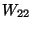 + 1/2, 0 =
+ 1/2, 0 = 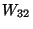 + 0 for
+ 0 for 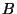 .
.One obtains
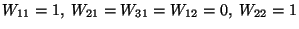 , and
, and 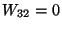 .
.Point
 : 0,0,1 is reflected to 0,0,
: 0,0,1 is reflected to 0,0,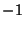 and then shifted to 1/2,1/2,
and then shifted to 1/2,1/2,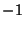 .
.This means
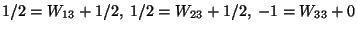 or
or 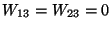 ,
, 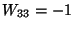 .
. - (c)
-
The matrix-column pair is thus
W =
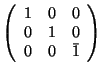 and w =
and w = 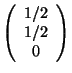 .
.
Example 2 [Draw a diagram !]
What is the pair (W,w) for an anti-clockwise 4-fold rotoinversion ![]() if the rotoinversion axis is parallel to c, and 1/2,1/2,1/2 is the inversion point ?
if the rotoinversion axis is parallel to c, and 1/2,1/2,1/2 is the inversion point ?
- (a)
- The anti-clockwise 4-fold rotation maps the origin onto the point 1,0,0; the following inversion in 1/2,1/2,1/2 maps this intermediate point onto the point 0,1,1, such that
 .
. - (b)
-
For the other points:
The equations are
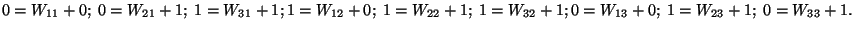
- (c)
- The result is W =
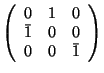 ; w =
; w = 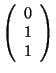 .
.
The resulting matrix-column pair is checked by mapping the fixed point 1/2,1/2,1/2 and the point 1/2,1/2,0. Their images are 1/2,1/2,1/2 and 1/2,1/2,1 in agreement with the geometric meaning of the operation.
Procedure 2
If the images of the origin and/or the coordinate points are not known, other pairs 'point-image point' must be used. It is difficult to give general rules but often fixed points are appropriate in such a case. In addition, one may exploit the different transformation behaviour of point coordinates and vector coefficients, see Section 4.4. Vector coefficients 'see' only the matrix W and not the column w, and that may facilitate the solution. Nevertheless, the calculations may now become more involved. The next example is not crystallographic in the usual sense, but related to twinning in 'spinel' mineral.
Example 3
What is the pair (W,w) for a 2-fold rotation about the space diagonal [111] with the point 1/2,0,0 lying on the rotation axis ?
It is not particularly easy to find the coordinates of the image ![]() of the origin
of the origin ![]() . Therefore, another procedure seems to be more promising. One can use the transformation behaviour of the vector coefficients of the direction [111] and other distinguished directions. The direction [111] is invariant under the 2-fold rotation, and the latter is described by the matrix part only, see Section 4.4. Therefore, the following equations hold
. Therefore, another procedure seems to be more promising. One can use the transformation behaviour of the vector coefficients of the direction [111] and other distinguished directions. The direction [111] is invariant under the 2-fold rotation, and the latter is described by the matrix part only, see Section 4.4. Therefore, the following equations hold
On the other hand, the directions [1![]() 0], [01
0], [01![]() ], and [
], and [![]() 01] are perpendicular to [111] and thus are mapped onto their negative directions. This means
01] are perpendicular to [111] and thus are mapped onto their negative directions. This means
From the equations (5.1.2) one concludes
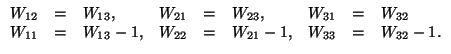
Together with equations (5.1.1) one obtains
![]() .
.
Thus, W = 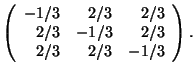
The point 1/2 0 0 is a fixed point, thus
![]() ,
,
![]() , and
, and
![]() .
.
The coefficients of w are then: ![]()
There are different tests for the matrix: It is orthogonal, its order is 2 (because it is orthogonal and symmetric), its determinant is ![]() , it leaves the vector
, it leaves the vector ![]() invariant, and maps the vectors
invariant, and maps the vectors ![]() , and
, and ![]() onto their negatives (as was used for its construction). The matrix-column pair can be tested with the fixed points, e.g. with
onto their negatives (as was used for its construction). The matrix-column pair can be tested with the fixed points, e.g. with ![]() ; with
; with ![]() ; or other points on the rotation axis.
; or other points on the rotation axis.
Problem 1B. Symmetry of the square. For the solution, see p. ![[*]](crossref.gif) .
.
Problem 1A, p. ![[*]](crossref.gif) , dealt with the symmetry of the square, see Fig. 3.4.1.
, dealt with the symmetry of the square, see Fig. 3.4.1.
There are 2 more questions concerning this problem.
- (v)
- Calculate the matrix-column pairs of the symmetry operations of the square.
- (vi)
-
Construct the multiplication table of the group of the square. [The multiplication table of a group
 of order
of order  is a table with
is a table with  rows and
rows and 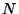 columns. The elements of the group are written on top of the table and on the left side, preferably in the same sequence and starting with the unit element. In the intersection of the
columns. The elements of the group are written on top of the table and on the left side, preferably in the same sequence and starting with the unit element. In the intersection of the 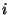 th row and the
th row and the 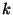 th column the product
th column the product 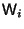
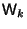 is listed for any pair of indices
is listed for any pair of indices 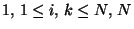 . The complete table is the multiplication table].
. The complete table is the multiplication table].
Are there remarkable properties of the multiplication table ?
The geometric meaning of (W,w)
How can one find the geometric meaning of a matrix-column pair ? Large parts of the following recipe apply not only to crystallographic symmetry operations but also to general isometries.
- One must know the reference coordinate system of the matrix-column pair. Without this knowledge a geometric evaluation is impossible.
Example. The matrix (in IT A shorthand notation)
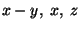 describes a 6-fold anti-clockwise rotation if referred to a hexagonal basis. If referred to an orthonormal basis it does not describe an isometry at all but contains a shearing component.
describes a 6-fold anti-clockwise rotation if referred to a hexagonal basis. If referred to an orthonormal basis it does not describe an isometry at all but contains a shearing component. - The matrix part is evaluated first.
In general the coefficients of the matrix depend on the choice of the basis; a change of basis changes the coefficients, see Section 5.3.2. However, there are geometric quantities which are independent of the basis. Correspondingly, there exist characteristic numbers of a matrix from which the geometric features may be derived and vice versa.
- The preservation of the 'handedness' of an object, i.e. the question if the symmetry operation is a rotation or rotoinversion is a geometric property. The corresponding property of the matrix is its determinant:
- The angle of rotation
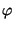 . It does not depend on the coordinate basis. The corresponding invariant of the matrix W is the trace, it is defined by
. It does not depend on the coordinate basis. The corresponding invariant of the matrix W is the trace, it is defined by
The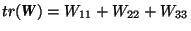 . The rotation angle
. The rotation angle  of the rotation or of the rotation part of a rotoinversion can be calculated from the trace by the formula
of the rotation or of the rotation part of a rotoinversion can be calculated from the trace by the formula sign is used for rotations, the
sign is used for rotations, the  sign for rotoinversions.
sign for rotoinversions.
One can list this correlation in a table
| tr(W) | 3 | 2 | 1 | 0 | 0 | 1 | ||||
| type | 1 | 6 | 4 | 3 | 2 | |||||
| order | 1 | 6 | 4 | 3 | 2 | 2 | 6 | 4 | 6 | 2 |
By this table the type of operation may be found, as far as it is determined by the matrix part. For example, one takes from the table that a specific operation is a two-fold rotation but one does not know if the operation is a rotatation or a screw rotation, what the direction of the rotation axis is and where it is located in space. This characterization will be done in the following list for the crystallographic symmetry operations.
- Type 1 or
 : no preferred direction
: no preferred direction
- All other symmetry operations have a preferred axis (the rotation or rotoinversion axis). The direction u of this axis may be determined from the equation
The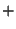 sign is for rotations, the
sign is for rotations, the  sign for rotoinversions.
sign for rotoinversions.
For type
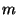 , reflections or glide reflections, u is the direction of the normal of the (glide) reflection plane.
, reflections or glide reflections, u is the direction of the normal of the (glide) reflection plane. - If W is the matrix of a rotation of order
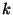 or of a reflection (
or of a reflection (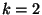 ), then
), then 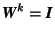 , and one determines the intrinsic translation part, also called screw part or glide part
, and one determines the intrinsic translation part, also called screw part or glide part 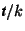 by
The vector with the column of coefficients
by
The vector with the column of coefficients 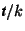 is called the screw or glide vector. This vector is invariant under the symmetry operation:
is called the screw or glide vector. This vector is invariant under the symmetry operation: 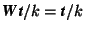 : Indeed, multiplication with W permutes only the terms on the right side of equation 5.2.5. Thus, the screw vector of a screw rotation is parallel to the screw axis. The glide vector of a glide reflection is left invariant for the same reason. Therefore, it is parallel to the glide plane.
: Indeed, multiplication with W permutes only the terms on the right side of equation 5.2.5. Thus, the screw vector of a screw rotation is parallel to the screw axis. The glide vector of a glide reflection is left invariant for the same reason. Therefore, it is parallel to the glide plane.
If t = o holds, then (W,w) describes a rotation or reflection. For
The column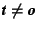 , (W,w) describes a screw rotation or glide reflection. One forms the so-called reduced operation by subtracting the intrinsic translation part t/k from (W,w):
, (W,w) describes a screw rotation or glide reflection. One forms the so-called reduced operation by subtracting the intrinsic translation part t/k from (W,w):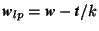 is called the location part because it determines the position of the rotation or screw-rotation axis or of the reflection or glide-reflection plane in space.
is called the location part because it determines the position of the rotation or screw-rotation axis or of the reflection or glide-reflection plane in space.
If W is a diagonal matrix, i.e. if only the coefficients
 are non-zero, then either is
are non-zero, then either is 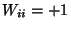 and
and 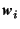 is a screw or glide component, or
is a screw or glide component, or 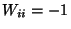 and
and 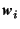 is a location component. If W is not a diagonal matrix, then the location part
is a location component. If W is not a diagonal matrix, then the location part 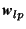 has to be calculated according to equation 5.2.6.
has to be calculated according to equation 5.2.6. - The fixed points are obtained by solving the equation
Equation (5.2.7) has a unique solution for all rotoinversions (including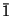 , excluding
, excluding 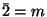 ). There is a 1-dimensional set of solutions for rotations (the rotation axis) and a 2-dimensional set of solutions for reflections (the mirror plane). For screw rotations and glide reflections, there are no solutions: there are no fixed points. However, a solution is found for the reduced operation, i.e. after subtraction of the intrinsic translation part, by equation 5.2.8
). There is a 1-dimensional set of solutions for rotations (the rotation axis) and a 2-dimensional set of solutions for reflections (the mirror plane). For screw rotations and glide reflections, there are no solutions: there are no fixed points. However, a solution is found for the reduced operation, i.e. after subtraction of the intrinsic translation part, by equation 5.2.8
The formulae of this section enable the user to find the geometric contents of any symmetry operation. In reality, IT A have provided the necessary information for all symmetry operations which are listed in the plane-group or space-group tables. The entries of the General position are numbered. The geometric meaning of these entries is listed under the same number in the block Symmetry operations in the tables of IT A. The explanation of the symbols for the symmetry operations is found in Sections 2.9 and 11.2 of IT A.
The section shall be closed with an exercise.
Problem 2B. Symmetry described by matrix-column pairs.
For the solution, see p. ![[*]](crossref.gif) .
.
The matrix-column pairs (A,a), (B,b) (C,c), and (D,d) have been listed or derived in Problem 2A, p. ![[*]](crossref.gif) , which dealt with their combination and reversion.
, which dealt with their combination and reversion.
Question
- (viii)
-
Determine the geometric meaning of the matrix-column pairs
(A,a), (B,b), (C,c), and (D,d).
Coordinate transformations
There are several reasons to change the coordinate system. Some examples for such reasons are the following:
- If one and the same crystal structure is described in different coordinate systems by different authors, then the structural data e.g. lattice constants, atomic coordinates, or displacement parameters (thermal parameters) have to be transformed to the same coordinate system in order to be comparable. The same holds for the comparison of related crystal structures.
- In phase transitions frequently the phases are related by their symmetries, e.g. in phase transitions of the second order. Often the conventional setting of the new phase is different from that of the original one. Then a change of the coordinate system may be necessary in order to find the structural changes which are connected with the phase transition.
- In the physics of macroscopic crystals (thermal expansion, dielectric constant, elasticity, piezoelectricity, etc.) the properties are described mostly relative to an orthonormal basis. Therefore, for physical calculations the direction and Miller indices etc. have to be transformed from the conventional crystallographic to an orthonormal basis.
- In IT A, 44 space-group types are described in more than one conventional coordinate system. The transition from one description to the other may be necessary and needs coordinate transformations.
Origin shift
At first the consequences of an origin shift are considered. We start from Fig. 1.4.1 on p. ![[*]](crossref.gif) where
where ![]() is the origin with the zero column o as coordinates, and
is the origin with the zero column o as coordinates, and ![]() is a point with coordinate column x. The new origin is
is a point with coordinate column x. The new origin is ![]() with coordinate column (referred to the old origin)
with coordinate column (referred to the old origin) ![]() , whereas
, whereas ![]() are the coordinates of
are the coordinates of ![]() with respect to the new origin
with respect to the new origin ![]() . This nomenclature is consistent with that of IT A, see Section 5.1 of IT A.
. This nomenclature is consistent with that of IT A, see Section 5.1 of IT A.
For the columns, ![]() holds, or
holds, or
[It may look strange to write the simple equation (5.3.1) in the complicated form of (5.3.2). The reason will become apparent later in this section].
Equation (5.3.2) can be written in augmented matrices ![]() with
with
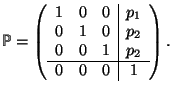 A distance vector
A distance vector 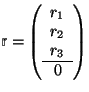 is not changed by the transformation
is not changed by the transformation ![]() because the column
because the column ![]() is not effective, see Sections 4.3 and 4.4.
is not effective, see Sections 4.3 and 4.4.
How do the matrix and column parts of an isometry change if the origin is shifted ? In the old coordinate system ![]() holds, in the new one is
holds, in the new one is ![]() . By application of equation (5.3.2) one obtains
. By application of equation (5.3.2) one obtains
Comparison with ![]() yields
yields
| (5.3.3) |
Conclusion. A change of origin does not change the matrix part of an isometry. The change of the column w does not only depend on the shift p of the origin, but also on the matrix part W.
How is a screw or glide component changed by an origin shift, i.e. what happens if one replaces in ![]() of equation 5.2.4 the column w by
of equation 5.2.4 the column w by ![]() ? The answer is simple: the additional term
? The answer is simple: the additional term
![]() does not contribute because
does not contribute because
![]()
An origin shift does not change the screw or glide component of a symmetry operation. The component ![]() is the component of p which is vertical to the screw-rotation or rotation axis or to the mirror or glide plane. It causes a change of the location part
is the component of p which is vertical to the screw-rotation or rotation axis or to the mirror or glide plane. It causes a change of the location part ![]() of the symmetry operation.
of the symmetry operation.
Change of basis
A change of basis is mostly described by a ![]() matrix
matrix ![]() by which the new basis vectors are given as linear combinations of the old basis vectors:
by which the new basis vectors are given as linear combinations of the old basis vectors:
By inserting equation (5.3.5) one obtains
The transformation of an isometry follows from equation (5.3.6) and from the relation ![]() by comparison with
by comparison with ![]() :
:
![]() or
or ![]()
From this follows
Example
In Fig. 1.5.2 on p. ![[*]](crossref.gif) the conventional and a primitive basis are defined for a plane group of the rectangular crystal system. If
the conventional and a primitive basis are defined for a plane group of the rectangular crystal system. If ![]() is the conventional,
is the conventional, ![]() the primitive basis, then
the primitive basis, then
P = 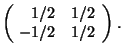 One finds
One finds 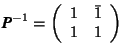 either by trial and error or with equation (2.6.1) on p.
either by trial and error or with equation (2.6.1) on p. ![[*]](crossref.gif) .
.
For the coordinates, ![]() holds. The conventional coordinates 1,0 of the endpoint of a become 1,1 in the primitive basis; those of the endpoint 1/2,1/2 of a
holds. The conventional coordinates 1,0 of the endpoint of a become 1,1 in the primitive basis; those of the endpoint 1/2,1/2 of a![]() become 0,1; those of the endpoint 0,1 of b become
become 0,1; those of the endpoint 0,1 of b become ![]() .
.
If the endpoints of the lattice-translation vectors of Fig. 1.5.2 on p. ![[*]](crossref.gif) , and those of their integer linear combinations are marked with points, a point lattice is obtained.
, and those of their integer linear combinations are marked with points, a point lattice is obtained.
Suppose, the origin is in the upper left corner of the unit cell of Fig. 1.5.2. Then, the reflection through the line 'a' is described by the matrix-column pair
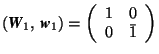 ,
,  ;
;
the reflection through the parallel line through the endpoint of the vector
![]() is described by
is described by 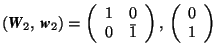 .
.
The column ![]() is the o column because
is the o column because ![]() is the o column. According to equation (5.3.8),
is the o column. According to equation (5.3.8),
the column ![]() is obtained from
is obtained from ![]() by
by 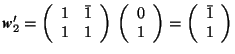 .
.
Indeed, this is the image of the origin, expressed in the new basis. All these results agree with the geometric view.
General coordinate transformations
In general both the origin and the basis have to be changed. One can do this in 2 different steps. Because the origin shift p is referred to the old basis ![]() , it has to be performed first:
, it has to be performed first:
In the usual way one concludes from equation (5.3.9) together with
![]()
The second equation may be written
In ![]() matrices the equation (5.3.10) is written
matrices the equation (5.3.10) is written
(with ![]() , and
, and ![]() )
)
This shape of equation (5.3.10 ) facilitates the formulation but not the actual calculation. For the latter, the forms 5.3.11 or 5.3.12 are more appropriate.
![Fig 5.3.3]](https://www.iucr.org/__data/assets/image/0009/15012/coch.gif)
Fig. 5.3.3 Diagram of 'mapping of mappings'.
The formalism of transformations can be displayed by the diagram of Fig. 5.3.3. The points ![]() (left) and
(left) and ![]() (right) are represented by the original coordinates
(right) are represented by the original coordinates ![]() und
und ![]() (top) and the new coordinates
(top) and the new coordinates ![]() und
und ![]() (bottom). At the arrows the corresponding transformations are denoted. They describe from left to right a mapping, from top to bottom the change of coordinates. Equation 5.3.10 is read from the figure immediately: On the one hand one reads
(bottom). At the arrows the corresponding transformations are denoted. They describe from left to right a mapping, from top to bottom the change of coordinates. Equation 5.3.10 is read from the figure immediately: On the one hand one reads ![]() along the lower edge; on the other hand taking the way up
along the lower edge; on the other hand taking the way up ![]() left
left ![]() down one finds
down one finds
Both ways start at the same point and end at the same point. Therefore, the one way can be equated to the other, and herewith equation 5.3.10 is derived in a visual way.
Remark. If there are different listings of the same crystal structure or of a set of related crystal structures, it is often not sufficient to transform the data to the same coordinate system. Even after such a transformation the coordinates of the atoms may be incomparable. The reason is the following:
In IT A for each (general or special) Position the full set of representatives ![]() is listed, see the table in Section 4.6. After insertion of the actual coordinates one has a set of triplets of numbers, 24 (including the centering) in the table of Section 4.6. Any one of these representatives may be chosen to describe the structure in a listing; the others can be generated from the selected one. The following Problem shows that different choices happen in reality. For a comparison of the structures it is then necessary to choose for the description corresponding atoms in the structures to be compared.
is listed, see the table in Section 4.6. After insertion of the actual coordinates one has a set of triplets of numbers, 24 (including the centering) in the table of Section 4.6. Any one of these representatives may be chosen to describe the structure in a listing; the others can be generated from the selected one. The following Problem shows that different choices happen in reality. For a comparison of the structures it is then necessary to choose for the description corresponding atoms in the structures to be compared.
Problem 3. Change of the coordinate system.
In R. W. G. Wyckoff, Crystal structures, vol. II, Ch. VIII, one finds the important mineral zircon ![]() and a description of its crystal structure under (VIII,a4) on text p. 5, table p. 9, and Figure VIIIA,4. Many rare-earth phosphates, arsenates, and vanadates belong to the same structure type. They are famous for their interesting magnetic properties.
and a description of its crystal structure under (VIII,a4) on text p. 5, table p. 9, and Figure VIIIA,4. Many rare-earth phosphates, arsenates, and vanadates belong to the same structure type. They are famous for their interesting magnetic properties.
Structural data: Space group ![]() , No. 141;
, No. 141;
lattice constants a = 6.60 Å; c = 5.88 Å.
The origin choice is not stated explicitly. However, Wyckoff's Crystal Structures started to appear in 1948, when there was one conventional origin only (the later ORIGIN CHOICE 1, i.e. Origin at ![]() ).
).
![$ \begin{array}{rcl} Zr:& (a)&\ 0,0,0;\ 0,\frac{1}{2},\frac{1}{4};\ \frac{1}{2},... ...x{and the same with}\ (\frac{1}{2},\frac{1}{2},\frac{1}{2})+\,]. \end{array} $](https://www.iucr.org/__data/assets/image/0005/15764/img741.gif)
The parameters ![]() and
and ![]() are listed with
are listed with ![]() = 0.20 and
= 0.20 and ![]() = 0.34.
= 0.34.
In the Structure Reports, vol. 22, (1958), p. 314 one finds:
'a = 6.6164(5) Å, c = 6.0150(5) Å'
'Atomic parameters. Origin at center (![]() ) at
) at ![]() from
from ![]() .'
.'
'Oxygen: (![]() ) with
) with ![]() = 0.067,
= 0.067, ![]() = 0.198.'
= 0.198.'
In order to compare the different data, the parameters of Wyckoff's book are to be transformed to 'origin at center 2/![]() ', i.e. ORIGIN CHOICE 2.
', i.e. ORIGIN CHOICE 2.
Questions
- (i)
- What are the new coordinates of the
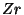 atoms ?
atoms ? - (ii)
- What are the new coordinates of the
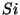 atoms ?
atoms ? - (iii)
- What are the new coordinates of the
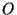 atom at
atom at  ?
? - (iv)
- What are the new coordinates of the other
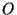 atoms ?
atoms ?
For a physical problem it is advantageous to refer the crystal structure onto a primitive cell with origin in 2/![]() . The choice of the new basis is
. The choice of the new basis is
![]() ).
).
Questions
- (v)
- What are the new coordinates of the first
 atom ?
atom ? - (vi)
- What are the new coordinates of the first
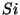 atom ?
atom ? - (vii)
- What are the new coordinates of the
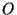 atom originally at 0,
atom originally at 0,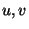 ?
?
Solution of the exercises
Solution of problem 1
Solution 1A. Symmetry of the square. For the problems, see p. ![[*]](crossref.gif) .
.
Answers
- (i)
-
The symmetry operations of the square are:
- the mapping 1
 1, 2
1, 2  2, 3
2, 3  3, and 4
3, and 4  4;
4; - the mapping 1
 3, 2
3, 2  4, 3
4, 3  1, and 4
1, and 4  2;
2; - the mapping 1
 2, 2
2, 2  3, 3
3, 3  4, and 4
4, and 4  1;
1; - the mapping 1
 4, 2
4, 2  1, 3
1, 3  2, and 4
2, and 4  3;
3; - the mapping 1
 2, 2
2, 2  1, 3
1, 3  4, and 4
4, and 4  3;
3; - the mapping 1
 4, 2
4, 2  3, 3
3, 3  2, and 4
2, and 4  1;
1; - the mapping 1
 3, 3
3, 3  1, which maps the points 2 and 4 onto themselves (leaves them invariant);
1, which maps the points 2 and 4 onto themselves (leaves them invariant); - the mapping 2
 4, 4
4, 4  2, which maps the points 1 and 3 onto themselves (leaves them invariant).
2, which maps the points 1 and 3 onto themselves (leaves them invariant).
- the mapping 1
- (ii)
-
The symmetry operations are, respectively:
(a) the identity operation 1, (b) the two-fold rotation 2,
(c) the four-fold rotation 4 =
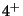 (anti-clockwise),
(anti-clockwise),(d) the four-fold rotation
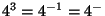 (clockwise),
(clockwise),(e) the reflection
 in the line
in the line  ,
,(f) the reflection
 in the line
in the line 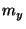 ,
,(g) the reflection
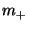 in the line
in the line 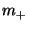 ,
,(h) and the reflection
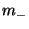 in the line
in the line 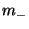 .
. - (iii)
-
The orders of these symmetry operations are, respectively:
1, 2, 4, 4, 2, 2, 2, and 2.
- (iv)
- There are altogether 8 symmetry operations.
Solution 1B. Symmetry of the square. For the problems, see p. ![[*]](crossref.gif) .
.
Answers
- (v)
-
The determination of the matrix-column pairs is particularly easy because the origin
 is a fixed point under all symmetry operations of the square. Therefore, for all of them w = o holds. The images of the coordinate points 1,0 and 0,1 and their coordinates are easily found visually. The matrices are:
is a fixed point under all symmetry operations of the square. Therefore, for all of them w = o holds. The images of the coordinate points 1,0 and 0,1 and their coordinates are easily found visually. The matrices are:
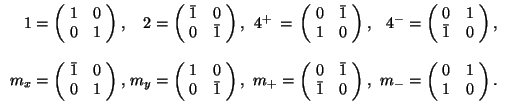
- (vi)
-
The multiplication table of the group of the square is
![\begin{displaymath}\hspace{-15mm}\begin{array}{\vert c\vert cccccccc\vert} \hlin... ...m_x&4^{-1}&2&4&1\rule[-1.3ex]{0em}{2ex}\\ \hline \end{array}. \end{displaymath}](https://www.iucr.org/__data/assets/image/0006/15783/img760.gif)
Remarkable properties of the multiplication table are
- If there is a '1' in the main diagonal of the table, then the element is the unit element or has order 2 and vice versa. This is easy to see.
- One finds that in each row and in each column each element of the group occurs exactly once. This is a property of the multiplication table of any group. It is not difficult to prove but the proof needs elementary group theory.
Solution of problem 2
Solution 2A. Symmetry described by matrices.
Answers
- (i)
-
(B,b)(A,a): BA =
 , Ba =
, Ba = 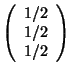 ,
,
Ba + b = Ba for b = o.Therefore, (BA,Ba + b) = (C,c) =
 ,
, 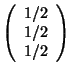 .
. - (ii)
-
Analogously one calculates
(A,a)(B,b) = (D,d) =
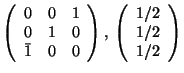 .
. - (iii)
- (A,a)
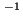 =
= 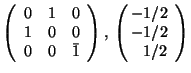 .
. - (iv)
- (B,b)
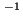 =
= 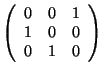 ,
,  .
. - (v)
- (C,c)
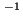 =
=  ,
, 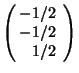 .
. - (vi)
- (D,d)
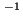 =
= 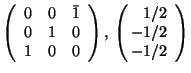 .
. - (vii)
-
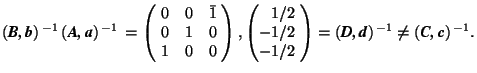
Note, that (B,b)
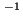 (A,a)
(A,a)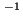 = [(A,a)(B,b)]
= [(A,a)(B,b)]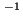 = (D,d)
= (D,d)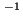 .
.
Solution 2B. Symmetry described by matrices.
Answer
- (viii)
-
We follow the procedure described in Section 5.2.
From the matrix parts the 'types' of the operations are determined by the determinants and traces: 
All the matrices are those of rotations. The directions [uvw] of the rotation axes are determined by applying equation (5.2.3): ![\( \begin{array}{\vert llll\vert}\hline \multicolumn{1}{\vert c}{\rule[-1mm]{0mm... ...lumn{1}{c}{[1\,0\,0]}&\multicolumn{1}{c\vert}{[0\,1\,0]}\\ \hline \end{array} \)](https://www.iucr.org/__data/assets/image/0010/15796/img773.gif)
It is more or less a matter of taste and experience if one continues with the calculation of the screw part (possibly o) by equation 5.2.5 or if one calculates the (possibly non-existing) fixed points by equation 5.2.7. If the order of the matrix is low then the calculation of the screw part is not so costly as if the order is high. If the screw part turns out to be o or if there are no fixed points then the calculation was not quite in vain because one then knows that the other way will be successful.
'Obviously' the pair (B,b) describes a rotation because the column
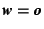 indicates the origin
indicates the origin 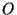 to be a fixed point. Solution: (B,b) describes a 3-fold rotation with rotation axis [111] and the points
to be a fixed point. Solution: (B,b) describes a 3-fold rotation with rotation axis [111] and the points 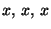 (including 0,0,0) as fixed points.
(including 0,0,0) as fixed points.We decide to calculate the screw parts in all other cases. Because of the order 2, the calculation for (A,a) is short. The pairs (C,c) and (D,D) can not have fixed points because in both cases a '
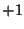 ' in the main diagonal is combined with a non-zero coefficient
' in the main diagonal is combined with a non-zero coefficient 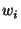 in the column. This
in the column. This 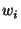 is a screw coefficient, see the remark on diagonal matrices in Section 5.2. We start with (A,a).
is a screw coefficient, see the remark on diagonal matrices in Section 5.2. We start with (A,a).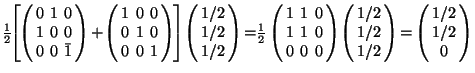
is the screw part of (A,a).
The reduced operation is
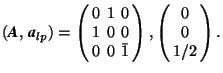
Equation 5.2.8 yields
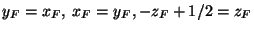 and the fixed points
and the fixed points 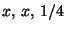 , with arbitrary
, with arbitrary 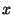 . The fixed points are not really fixed points of the symmetry operation but are the coordinates of the screw-rotation axis
. The fixed points are not really fixed points of the symmetry operation but are the coordinates of the screw-rotation axis 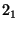 .
.The calculation for (C,c) is a bit more lengthy:
![$\frac{\mbox{\textit{\textbf{t}}}}{4}\hspace{-0.5mm}=\hspace{-0.5mm}\frac{1}{4}\... ...ht]\hspace{-0.5mm} \left(\begin{array}{c} 1/2\\ 1/2\\ 1/2 \end{array}\right)=$](https://www.iucr.org/__data/assets/image/0016/15802/img779.gif)
=
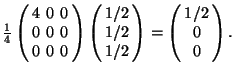
The symmetry operation is a 4-fold screw rotation with
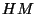 symbol
symbol 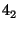 .
.The points of the screw axis are determined by equation 5.2.8 again:
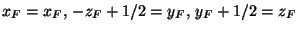 result in
result in 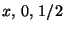 with arbitrary
with arbitrary 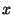 .
.Analogously one determines (D,d) to describe a 4-fold screw rotation
 , the screw axis in
, the screw axis in 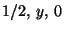 , with arbitrary
, with arbitrary 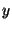 .
.
Solution of problem 3
Solution 3. Change of the coordinate system.
The new origin ![]() has the coordinates
has the coordinates ![]() referred to the present origin
referred to the present origin ![]() . Therefore, the change of coordinates consists of subtracting 0,
. Therefore, the change of coordinates consists of subtracting 0, ![]() from the old values, i.e. leave the
from the old values, i.e. leave the ![]() coordinate unchanged, add
coordinate unchanged, add ![]() to the
to the ![]() coordinate, and subtract
coordinate, and subtract ![]() from the
from the ![]() coordinate.
coordinate.
Answers
The new coordinates are
- (i)
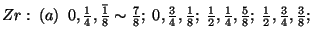
- (ii)
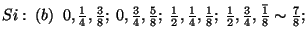
- (iii)
-
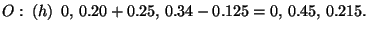
This oxygen atom is obviously not the one (0,0.067,0.198) listed by the Structure Reports but must be a symmetrically equivalent one. Therefore, it is necessary to determine also the new coordinates of the other oxygen atoms.
- (iv)
-
 The coordinates of the other oxygen atoms are (normalized
The coordinates of the other oxygen atoms are (normalized 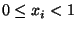 ):
):

The first one of these oxygen atoms corresponds to the one representing the results of the later refinement with higher accurancy. The
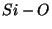 distance is reduced from 1.62 Å to 1.61 Å.
distance is reduced from 1.62 Å to 1.61 Å.
Answers
The change of basis to the primitive cell is described by the matrix
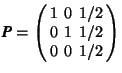 .
.
One determines the inverse matrix 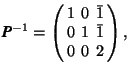
by which the coordinates are transformed using the formula (5.3.6):
![]() . The coordinates x are those referred to the origin in
. The coordinates x are those referred to the origin in ![]() .
.
- (v)
-
The new coordinates of the first
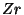 atom are
atom are
- (vi)
-
The new coordinates of the first
 atom are
atom are
- (vii)
-
The new coordinates of the first
 atom are
atom are
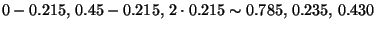 .
.
Index
- absolute value of a vector
- Vectors
- affine mapping
- Mappings and symmetry operations
- affine space
- Points and their coordinates
- angle
-
- calculation of
- Distances and angles
- angle of rotation
- The geometric meaning of
- associative
- Vectors | Rules for matrix calculations | Combination and reversion of
- augmented column
- (
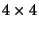 ) matrices
) matrices - augmented matrix
- (
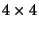 ) matrices
) matrices - axis
-
- of rotation
- Isometries | The geometric meaning of
- of rotoinversion
- Isometries | The geometric meaning of
- basis
-
Vector coefficients
- conventional
- The scalar product and
- orthonormal
- The scalar product and
- primitive
- The scalar product and | Space-group operations
- basis vectors
- Vector coefficients
- Cartesian coordinates
- Special coordinate systems: Cartesian
- center of inversion
- Isometries
- centered lattice
- The scalar product and
- coefficients of a vector
- Vector coefficients
- column index
- The matrix formalism
- column matrix
- The matrix formalism
- column, augmented
- (
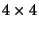 ) matrices
) matrices - commutative
- Vectors | Rules for matrix calculations
- conventional basis
- The scalar product and
- coordinate axes
- Points and their coordinates
- coordinate system
- Points and their coordinates
- coordinate transformation
- Points and their coordinates | Coordinate transformations | General coordinate transformations
- coordinates
- crystal class
- Crystallographic groups
- crystal pattern
- The scalar product and
- crystallographic symmetry operation
- The geometric meaning of
- dependent, linearly
- Vectors
- determinant
- The geometric meaning of
- diagonal matrix
- The matrix formalism
- dimension
- Vectors
- distance
-
- calculation of
- Distances and angles | Distances and angles | Distances and angles
- distributive
- Rules for matrix calculations
- Euclidean space
- Points and their coordinates
- finite group
- Crystallographic groups
- fixed point
- Isometries | The geometric meaning of
- fundamental matrix
- Distances and angles
- general position
- The 'General Position' in | The 'General Position' in
- glide part
- The geometric meaning of
- glide plane
- Isometries
- glide reflection
- Isometries | Space-group operations | The geometric meaning of
- glide vector
- Isometries | The geometric meaning of
- group
-
- finite
- Crystallographic groups
- infinite
- Crystallographic groups
- order of a
- Crystallographic groups
- Hermann-Mauguin symbol
- Crystallographic site-symmetry operations
- HM symbol
- Crystallographic site-symmetry operations
- identity
- Isometries | Combination and reversion of | The geometric meaning of
- image
- Mappings and symmetry operations
- improper isometry
- Isometries
- independent, linearly
- Vectors
- indices notation
- Rules for matrix calculations
- infinite group
- Crystallographic groups
- integer matrix
- The matrix formalism | The matrix-column pairs of
- intrinsic translation part
- The geometric meaning of
- intrinsic translation part
- The geometric meaning of
- inverse matrix
- Inversion of a matrix
- inversion
-
Isometries | Crystallographic site-symmetry operations | The geometric meaning of
- center of
- Isometries | The geometric meaning of
- isometric mapping
- Mappings and symmetry operations
- isometry
-
Mappings and symmetry operations | Isometries
- first kind
- Mappings and symmetry operations | Isometries
- improper
- Isometries
- order of
- Crystallographic site-symmetry operations
- proper
- Isometries
- second kind
- Isometries
- IT A
- List of symbols
- lattice
-
- centered
- The scalar product and
- primitive
- The scalar product and
- lattice basis
-
The scalar product and
- primitive
- The scalar product and
- lattice constants
- The scalar product and
- lattice vector
- The scalar product and
- law
- law of composition
- Combination and reversion of
- length of a vector
- Vectors
- linear combination
- Vector coefficients
- linearly dependent
- Vectors
- linearly independent
- Vectors
- location part
- The geometric meaning of
- mapping
-
Mappings and symmetry operations
- affine
- Mappings and symmetry operations
- isometric
- Mappings and symmetry operations
- non-singular
- Combination and reversion of
- regular
- Combination and reversion of
- matrix
-
The matrix formalism
- augmented
- (
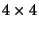 ) matrices
) matrices - diagonal
- The matrix formalism
- fundamental
- Distances and angles
- integer
- The matrix formalism | The matrix-column pairs of
- inverse
- Inversion of a matrix
- orthogonal
- Inversion of a matrix
- rational
- The matrix formalism
- regular
- Determinants
- singular
- Determinants
- symmetric
- The matrix formalism
- transposed
- The matrix formalism
- unit
- The matrix formalism
- matrix notation
- Motivation
- matrix product
- Rules for matrix calculations
- matrix-column pair
- Rules for matrix calculations | Matrix-column pairs
- mirror plane
- Isometries
- motion
- Mappings and symmetry operations
- multiplication table
- Determination of the matrix-column
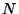 -fold
-fold- Crystallographic site-symmetry operations
- non-singular mapping
- Combination and reversion of
- O-matrix
- The matrix formalism
- o-vector
- Vectors
- orbit of points
- The 'General Position' in
- order of a group
- Crystallographic groups
- order of an isometry
- Crystallographic site-symmetry operations
- origin
- Points and their coordinates
- orthogonal matrix
- Inversion of a matrix
- orthonormal basis
- The scalar product and
- parallel coordinates
- Points and their coordinates | Special coordinate systems: Cartesian
- parallelogram of forces
- Vectors
- point group
- Crystallographic site-symmetry operations | Crystallographic groups | Crystallographic groups
- point lattice
- Change of basis
- point orbit
- The 'General Position' in
- point space
- Points and their coordinates
- position
-
- general
- The 'General Position' in | The 'General Position' in
- special
- The 'General Position' in
- primitive basis
- The scalar product and
- primitive lattice
- The scalar product and
- primitive lattice basis
- The scalar product and | Space-group operations
- product of matrices
- Rules for matrix calculations
- projection
- Mappings and symmetry operations | Combination and reversion of
- proper isometry
- Isometries
- rational matrix
- The matrix formalism
- reduced operation
- The geometric meaning of
- reflection
- Isometries | Crystallographic site-symmetry operations | The geometric meaning of
- reflection plane
- Isometries
- regular mapping
- Combination and reversion of
- regular matrix
- Determinants
- reverse operation
- Combination and reversion of
- rigid motion
- Mappings and symmetry operations
- rotation
- Isometries | Crystallographic site-symmetry operations | The geometric meaning of | The geometric meaning of
- rotation angle
- Isometries | The geometric meaning of
- rotation axis
- Isometries | The geometric meaning of
- rotoinversion
- Isometries | Crystallographic site-symmetry operations | Display of crystallographic symmetry | The geometric meaning of
- rotoinversion axis
- Isometries | The geometric meaning of
- row index
- The matrix formalism
- row matrix
- The matrix formalism
- scalar product
- Points and their coordinates | The scalar product and
- screw axis
- Isometries
- screw part
- The geometric meaning of
- screw rotation
- Isometries | Space-group operations | The geometric meaning of
- screw vector
- Isometries | Space-group operations | The geometric meaning of
- Seitz notation
- Matrix-column pairs
- singular matrix
- Determinants
- site symmetry
- Crystallographic site-symmetry operations | Crystallographic site-symmetry operations
- space
-
- affine
- Points and their coordinates
- point
- Points and their coordinates
- vector
- Vectors
- space group
- Crystallographic site-symmetry operations | Crystallographic groups
- space-group type
- Crystallographic groups | The 'General Position' in
- special position
- The 'General Position' in
- square matrix
- The matrix formalism
- subgroup
- Crystallographic groups
- symbol, Hermann-Mauguin
- Crystallographic site-symmetry operations
- symmetric matrix
- The matrix formalism
- symmetry
- Mappings and symmetry operations
- symmetry element
- Display of crystallographic symmetry
- symmetry operation
-
Mappings and symmetry operations | Display of crystallographic symmetry
- crystallographic
- Mappings and symmetry operations | The geometric meaning of
- symmorphic
- Crystallographic groups
- trace
- The geometric meaning of
- translation
- The scalar product and | Mappings and symmetry operations | Isometries | The geometric meaning of
- translation part, intrinsic
- The geometric meaning of | The geometric meaning of
- translation vector
- The scalar product and | Isometries
- transposed matrix
- The matrix formalism
- type of space groups
- Crystallographic groups | The 'General Position' in
- unit cell
- The volume of the
- unit matrix
- The matrix formalism
- unit vector
- Vectors
- vector
-
Vectors
- length of
- Vectors
- translation
- The scalar product and | Isometries
- unit
- Vectors
- vector coefficients
- Vector coefficients
- vector lattice
- The scalar product and
- vector space
- Vectors
- volume of the unit cell
- The volume of the