Introduction to the calculation of structure factors

S. C. Wallwork

In X-ray crystallography the structure factor F(hkl) of any X-ray reflection (diffracted beam) hkl is the quantity that expresses both the amplitude and the phase of that reflection. It plays a central role in the solution and refinement of crystal structures because it represents the quantity related to the intensity of the reflection which depends on the structure giving rise to that reflection and is independent of the method and conditions of observation of the reflection. The set of structure factors for all the reflections hkl are the primary quantities necessary for the derivation of the three-dimensional distribution of electron density, which is the image of the crystal structure, calculated by Fourier methods. This image is the crystallographic analogue of the image formed in a microscope by recombination of the rays scattered by the object. In a microscope this recombination is done physically by the lenses of the microscope but in crystallography the corresponding recombination of diffracted beams must be done by mathematical calculation.

The way in which the separate scattered or diffracted rays combine to form an image depends on three factors associated with each ray:

(a): the direction,
(b): the amplitude,
(c): the phase.

In the physical recombination of rays by the lenses of a microscope these three pieces of information about each ray are retained and used automatically in the recombination process. In X-ray crystallography, the diffracted beams are separately observed and their intensities measured as the blackness of spots on an X-ray film or by direct quantum counting in a diffractometer. By identifying the Miller indices (hkl) of the crystal plane giving rise to each diffracted beam, the direction of the beam is specified. From the measured intensity of the beam its amplitude may readily be deduced. So two of the three necessary pieces of information about each beam are known, but unfortunately there is no method available yet for observing the phase of each diffracted beam, which is the third piece of information needed before mathematical recombination is possible to produce an image of the structure. This constitutes what is known as the phase problem in crystallography.

The solution of a crystal structure therefore consists of applying some technique for obtaining the approximate phases of at least some of the X-ray reflections, and the process of structure refinement is one in which the knowledge of phases is extended to all reflections and is made as accurate as possible for all reflections. Apart from the direct methods of obtaining some initial phases, both the solution and refinement processes depend on the ability to calculate structure factors for a proposed approximate arrangement of some or all of the atoms in the crystal structure. This is the subject of this pamphlet. It will be seen that it is possible to calculate simultaneously both the amplitude $\vert F(hkl)\vert$ and phase $\alpha(hkl)$ of each beam that would be diffracted by the proposed structure. Since the phases cannot be compared with any observable quantities, the validity of the proposed structure must be tested by comparison of the calculated values of the amplitudes of the structure factor F_c with the observed amplitudes |F₀|. This is done by calculating a reliability index or R factor defined by

$\begin{displaymath} R={\sum \vert\vert F_0\vert - \vert F_c\vert\vert}\over{\sum\vert F_0\vert}\end{displaymath}$

where the summation is usually taken over all the reflections giving significant intensities. Because of random errors in the observed structure factor amplitudes |F₀|, and approximations made in the model on which the calculated structure factors are based, it is never possible to obtain a set of |F_c| which exactly reproduce the |F₀|, so structure refinement never reduces R to zero. For good quality diffractometer data, values of R in the region of 0.05 are quite common for fully refined structures. For initial approximate structures arising from the structure solution process R should not normally be greater than about 0.5 to be capable of satisfactory refinement.

A structure factor represents the resultant X-ray scattering power of the whole crystal structure, though, since the whole structure consists of a large number of unit cells all scattering in phase with each other, the resultant scattering power is actually calculated for the contents of one unit cell only. The structure factor therefore represents the resultant amplitude and phase of scattering of all the electron density distribution of one unit cell. The amplitude is calculated as the number of times greater it is than the amplitude of scattering from an isolated electron. The phase is calculated relative to a phase of zero for hypothetical scattering by a point at the origin of the unit cell. The resultant is calculated as a superimposition of waves, one from each atom in the unit cell, each wave having an amplitude which depends on the number of electrons in the atom and a phase which depends on the position of the atom in the unit cell.

Before seeing how to do this calculation in detail we must first see how wave motions of different amplitudes and phases can be combined. We consider the simplest case of the addition of a wave of amplitude f₁ and phase $\phi_1$ and a wave of amplitude f₂ and phase $\phi_2$ Each wave may be considered as a cosine function generated by projecting on to the horizontal diameter of a circle the positions of a point (P₁ or P₂) rotating with uniform velocity round the circle, (Fig. 1). The displacement of the projection on to the horizontal diameter may be taken as x. If each wave had a phase of zero, the radius connecting the points P₁ or P₂ with the centre of each circle would make the same angle $\nu$ with the horizontal diameter at the same moment in time, as shown in Fig. 1(a ), and the displacements on the horizontal diameters would be given by:

$\begin{displaymath} x_1=f_1\cos\nu \quad \hbox{and}\quad x_2=f_2\cos\nu.\end{displaymath}$

**Figure 1:** Generation and combination of two waveforms, (a) both with phase zero, (b) with phases $\phi_1$ and $\phi_2$ .
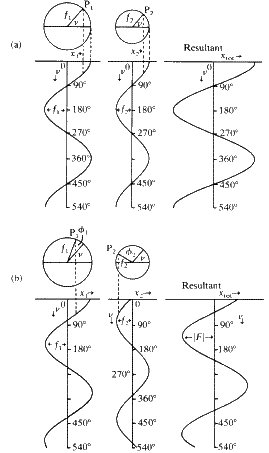$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

The sum of these two wave motions is simply a wave of the same phase with amplitude (f₁ + f₂). At any moment in time the total displacement is given by:

$\begin{displaymath} x_{\hbox{total}} =f_1\cos \nu + f_2\cos \nu = (f_1 + f_2)\cos \nu.\end{displaymath}$

When the first wave has a phase angle $\phi_1$ relative to the radius at the angle $\nu$ and the second wave has a phase angle $\phi_2$ relative to the same radius, the two component waves and their resultant are as shown in Fig. 1(b ). The resultant now has an amplitude which is less than (f₁ + f₂), because the component waves no longer completely reinforce one another, and its phase differs from the phase of either of the components. The displacements, x₁ and x₂ for the two component waves are now given by:

$\begin{displaymath} x_1=f_1\cos(\nu + \phi_1) \quad \hbox{and}\quad x_2=f_2\cos(\nu + \phi_2)\end{displaymath}$

and the displacement for the resultant wave is given by

$\begin{displaymath} x_{\hbox{total}} = x_1 + x_2 = f_1\cos(\nu +\phi_1) + f_2\cos(\nu +\phi_2).\end{displaymath}$

When the cosine terms are expanded this becomes

$\begin{displaymath} x_{\hbox{total}} = f_1\cos\nu\cos\phi_1 - f_1\sin\nu\sin\phi_1 + f_2\cos\nu\cos\phi_2 - f_2\sin\nu\sin\phi_2 \eqno(1)\end{displaymath}$

$\begin{displaymath} \phantom{x_{\hbox{total}}} = \cos\nu(f_1\cos\phi_1 + f_2\cos\phi_2) - \sin\nu(f_1\sin\phi_1 + f_2\sin\phi_2).\end{displaymath}$

As can be seen from Fig. 1 the resultant wave is another cosine wave of the same frequency as the component waves but of different phase which we will call $\alpha$ . It can therefore be represented by:

$\begin{displaymath} x_{\hbox{total}} = \vert F\vert\cos (\nu + \alpha), \quad\hbox{where } \vert F\vert \hbox{ is the resultant amplitude}.\end{displaymath}$

Expanding this, we have

$\begin{displaymath} x_{\hbox{total}} = \vert f\vert\cos\nu\cos\alpha - \vert F\vert\sin\nu\sin\alpha. \eqno(2)\end{displaymath}$

Comparing equation (2) with equation (1), we see that

$\begin{displaymath} \vert F\vert\cos\alpha =f_1\cos\phi_1 + f_2\cos\phi_2.\quad\hbox{We call this } A'.\end{displaymath}$

$\begin{displaymath} \vert F\vert\sin\alpha =f_1\sin\phi_1 + f_2\sin\phi_2.\quad\hbox{We call this } B'.\end{displaymath}$

To find the amplitude |F| and phase $\alpha$ of the resultant wave we note that:

$\begin{displaymath} (A')^2+ (B')^2 = \vert F\vert^2\cos^2 \alpha + \vert F\vert^2\sin^2 \alpha = \vert F\vert^2\end{displaymath}$

and

$\begin{displaymath} (B')/(A') = (\vert F\vert\sin \alpha)/(\vert F\vert\cos \alpha) = \tan \alpha.\end{displaymath}$

In general, to find the resultant amplitude and phase for a wave composed of n cosine waves, of which a typical component j has amplitude f_j and phase $\phi_j$ , we have

$\begin{displaymath} A'=\vert F\vert\cos\alpha= \sum_{j=1}^n f_j\cos\phi_j \eqno(3)\end{displaymath}$

$\begin{displaymath} B'=\vert F\vert\sin\alpha= \sum_{j=1}^n f_j\sin\phi_j \eqno(4)\end{displaymath}$

and |F| and $\alpha$ are related to A' and B' as in the case of two components.

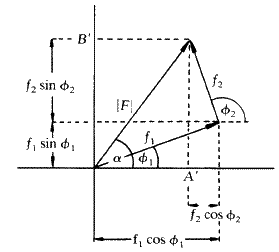
This addition of components may be represented conveniently on a vector diagram as in Fig. 2, where the example of the addition of the same two components is again shown. It can be seen on this diagram that A' is the algebraic sum of the $f_j\cos\phi_j$ terms and B' is the algebraic sum of the $f_j\sin\phi_j$ terms. The resultant vector F is the vector sum of the two components and the square of its amplitude, |F²|, is shown by Pythagoras' theorem to be given by (A')² + (B')². The direction or phase of the resultant is given by the angle $\alpha$ , whose tangent is equal to B'/A'.

**Figure 2:** Combination of component waves of amplitudes f₁ and f₂ and phases $\phi_1$ and $\phi_2$ to give a resultant wave of amplitude |F| and phase $\alpha$ , represented as a process of vector addition.
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

It is conventional to represent the amplitude and phase of a wave by a complex number which may be expressed in the form a + ib or as $xe^{i\theta}$ $(=x\cos \theta+ ix\sin \theta)$ . In these representations, a or $x\cos \theta$ is the real part of the complex number and ib or $ix\sin \theta$ is the imaginary part. This is quite consistent with the vector representation of Fig. 2 in that A' represents the real part a of the complex wave F and iB' is the imaginary part ib. The horizontal axis of Fig. 2 should therefore be regarded as the real axis and the vertical axis as the imaginary axis of the conventional Argand diagram for representing complex numbers. In the exponential form of a complex wave, $xe^{i\theta}$ , the angle $\theta$ corresponds to the phase angle $\alpha$ of Fig. 2 and x corresponds to the amplitude |F|.

Having seen how waves may be added to give a resultant wave we are now in a position to apply this procedure to the addition of waves scattered by the different atoms of a unit cell to give a resultant structure factor F. We need to consider the amplitude f of the scattering from each atom and its phase $\phi$ . Both these quantities are best approached from the point of view of the Bragg treatment of X-ray diffraction, which will first be outlined.

The Braggs, father and son, considered the diffraction of X-rays by a crystal to be more conveniently thought of in terms of reflection from regularly spaced, parallel planes in the crystal. Like any reflection process the angle $\theta$ between the incident beam and the reflecting plane is equal to the angle between the reflected beam and the plane. Unlike specular reflection, however, only certain angles of incidence and reflection will give rise to appreciable intensity in the reflected beam. These are the angles for which the rays reflected by successive planes in the crystal differ in phase by a whole number of wavelengths. (This restriction arises because the problem is really one of diffraction.) The difference in phase is found by calculating the difference in path length for two successive rays.

Consider first two rays of the incident beam that strike successive crystal planes at points O and B, respectively, where OB is perpendicular to the crystal planes (Fig. 3a ). The extra distance travelled by the lower ray is calculated by drawing perpendicular wave-fronts OA and OC to the incident and diffracted beams, respectively. It is seen to be AB + BC. Since $\theta$ is the angle between AB and the crystal plane and between BC and the crystal plane, $\theta$ is also the angle between the perpendicular to AB (i.e. OA) or to BC (i.e. OC) and the perpendicular to the crystal planes (i.e. OB). This is shown on the enlarged part of the diagram in Fig. 3b . Now, from the triangles ABO and BCO:

$\begin{displaymath} AB = OB \sin \theta \quad\hbox{ and } BC= OB \sin \theta\break\end{displaymath}$

$\begin{displaymath} \phantom{AB} = d \sin \theta \phantom{\quad\hbox{ and } BC} = d \sin \theta\end{displaymath}$

since OB = d, the perpendicular spacing of the crystal planes. The total path difference between the two rays (AB + BC) is therefore equal to $2d sin \theta$ . For reinforcement of successive rays this path difference must be a whole number of wavelengths.

$\begin{displaymath} % latex2html id marker 353 \therefore n\lambda =2d sin \theta. \eqno(5)\end{displaymath}$

This is known as the Bragg equation or the Bragg law.

**Figure 3:** Bragg reflection by equally-spaced, parallel crystal planes. (a) Construction to calculate the relative phases of rays reflected at the points O, B and P. (b) Enlargement of part of (a).
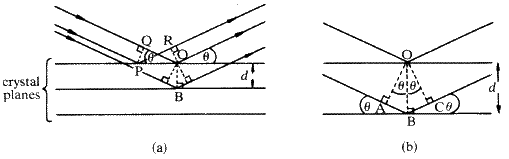$\begin{figure} \includegraphics {fig3.ps} \end{figure}$

Secondly we must show that the path difference is the same for two rays reflected from two successive crystal planes irrespective of the points on the planes at which they strike the planes. Consider the two rays reflected from the top plane at the points P and O. To check that there is no path difference between these two rays we construct the perpendiculars PQ and OR. The distance travelled by the ray reflected at O between the perpendicular wave fronts PQ and OR is QO. This is equal to $PO\cos \theta$ . The distance travelled by the ray reflected at P between the same two wave-fronts is PR. However, since the angle RPO is also $\theta$ , PR is also equal to $PO\cos \theta$ . The two rays are therefore in phase with each other throughout. This also means that if the phase difference between the rays reflected at O and B is $n\lambda$ after reflection, then the phase difference between the rays reflected at P and B is also $n\lambda$ after reflection. This establishes the principle that the phase difference between rays reflected from parallel planes in a crystal depends on the distances of the points of reflection measured perpendicular to the planes and not on the separation of the points of reflection measured parallel to the planes. Use is made of this principle both in considering how the amplitude of scattering of an atom depends on the Bragg angle $\theta$ and also in calculating how the phase of the scattered beam from each atom depends on its position in the unit cell.

If all the electrons in an atom were concentrated at one point, the amplitude of the X-rays scattered by the atom would simply be Z times the amplitude scattered by a single free electron, where Z is the atomic number of the atom. In fact, the electrons form a diffuse cloud of varying density, spherical in symmetry to a first approximation, but with quite high electron densities at, say, half the conventional atomic radius away from the centre of the atom. It is possible for the X-rays scattered from one part of the atom to be out of phase with those scattered from another part so that their contributions to the total scattering cancel instead of adding. The total amplitude of scattering by an atom will therefore, in general, be less than Z and will depend on the spacing of the parallel diffracting planes for the X-ray reflection under consideration.

**Figure 4:** The dependence of the relative phases of X-ray scattering, from two points O and P in an atom, on the interplanar spacing d of successive Bragg planes AB and CD (or C'D').
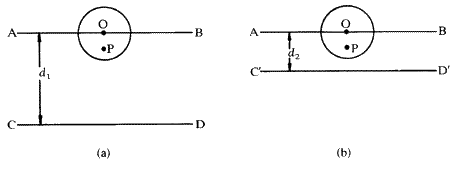$\begin{figure} \includegraphics {fig4.ps} \end{figure}$

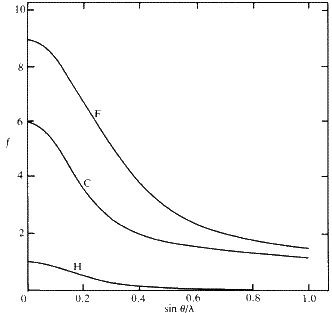
This may be understood by reference to Fig. 4. On the left is shown the situation where the spacing d₁ between the Bragg planes AB and CD is large compared with the atom centred at O. If the X-rays reflected at CD are one wavelength out of phase with the X-rays reflected at AB then a ray reflected from P will only be a small fraction of a wavelength out of phase with a ray reflected from O. The scattered rays from these two points will therefore largely reinforce each other. In fact, the scattering from all parts of the atom will largely add together to give a total amplitude f not much less than Z. In Fig. 4(b ), on the other hand, a different X-ray reflection is considered, where the spacing between the Bragg planes, d₂, is now of the same order of size as the atom. Now, the ray reflected from the point P will be almost exactly out of phase with the ray reflected from O. There will be destructive interference between them (not cancelling to zero, however, because the electron density, and therefore the amplitude of scattering at P, will be less than at O). In this situation the total amplitude of scattering f from the whole atom will be much less than Z. Since d and the Bragg angle $\theta$ are related by the Bragg equation (5), the situation of Fig. 4(a ) corresponds to a reflection at a small angle $\theta$ and the situation of Fig. 4(b ) corresponds to a large Bragg angle $\theta$ . In fact the amplitude of scattering from an atom f varies smoothly with $\sin \theta/\lambda$ in the manner shown for some typical atoms in Fig. 5. The amplitude f for an atom is called the atomic scattering factor. It extrapolates to Z as $\sin \theta/\lambda$ tends to zero because d tends to infinity and the differences of phase of scattering from different parts of the atoms tend to zero. When calculating a structure factor for a particular X-ray reflection hkl, the calculation is first of all carried out as though the scattering for each atom all took place from one point, the atomic centre. The effect of the distribution of electron density over an appreciable volume is then allowed for by multiplying the term for each atom by the atomic scattering factor f appropriate for the Bragg angle $\theta$ of the reflection.

**Figure 5:** Atomic scattering factors f for hydrogen, carbon and fluorine, plotted against $\sin \theta/\lambda$ .
$\begin{figure} \includegraphics {fig5.ps} \end{figure}$

We must now consider how the phase $\phi$ of scattering by an atom, as a contribution to a total structure factor F, depends on the position of the atom in the unit cell. The principle of the method is that the rays reflected by successive Bragg planes are one wavelength out of phase with each other and therefore differ in phase angle by $2\pi$ radians or 360 $^\circ$ . The hypothetical ray reflected from the origin of the cell always defines the phase angle zero, so the points of intersection of the plane hkl with the cell axes correspond to a phase of $2\pi$ radians or 360 $^\circ$ . The phase for the scattering by any atom in the unit cell (considered for this purpose as being at the point of its centre) is therefore given by its distance measured perpendicularly between a plane through the origin parallel to the plane hkl and the plane hkl itself. (It will be remembered that the phase is independent of the position parallel to the Bragg planes.) The calculation of the phase is best illustrated in two dimensions, as in Fig. 6.

**Figure 6:** Construction for calculating the phase of scattering from a point x, y in two dimensions for a reflection h, k.
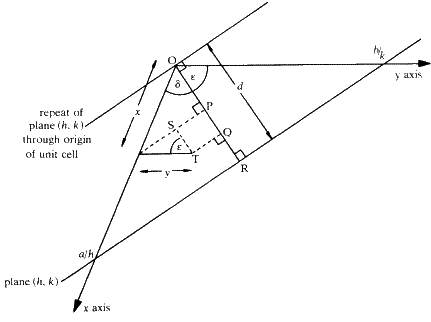$\begin{figure} \includegraphics {fig6.ps} \end{figure}$

The x and y axes of a two dimensional cell are shown intersected by the Bragg plane (actually a line) defined by the Miller indices h, k. From the definition of Miller indices, the intersection along the x axis occurs at a distance a/h from the origin O and the intersection along the y axis occurs at b/k where a and b are the unit cell dimensions along the x and y axes, respectively. The perpendicular spacing d between this plane and the parallel plane through the origin is given by the distance OR. Consider an atom at the point T, having coordinates x and y in the cell. We wish to know how far T is perpendicularly from the plane through O towards the plane through a/h, b/k, compared with the total perpendicular distance between these planes. It is convenient to measure all the perpendicular distances along the line OR, so the component of the distance due to the x coordinate is obtained by projecting the distance x onto OR as OP, and the component due to the y coordinate is obtained by projecting y onto OR as PQ. The total perpendicular distance of T from the plane through O is therefore OQ and it is calculated as follows:

$\begin{displaymath} OP =x\cos\delta\end{displaymath}$

$\begin{displaymath} PQ = ST = y\cos \varepsilon.\end{displaymath}$

But, from the triangle defined by O, R and the point a/h,

$\begin{displaymath} \cos\delta = {{OR}\over{a/h}} = {d\over{a/h}} = {dh\over a}\end{displaymath}$

and, from the triangle defined by O, R and the point b/k,

$\begin{displaymath} \cos\varepsilon = {{OR}\over{b/k}} = {d\over{b/k}} = {dk\over b}\end{displaymath}$

$\begin{displaymath} % latex2html id marker 601 \therefore OP=x\cdot{dh\over a} \quad\mathrm{and}\quad PQ=y\cdot{dk\over b}.\end{displaymath}$

$\begin{displaymath} OQ=OP+PQ=x\cdot{dh\over a} + y\cdot{dk\over b}\end{displaymath}$

$\begin{displaymath} % latex2html id marker 605 \therefore {OO\over d} = \left({hx\over a} + {ky\over b}\right).\end{displaymath}$

Now OR or distance d corresponds to a phase change of $2\pi$ radians. So OQ corresponds to a phase change of $OQ.2\pi/d$ radians. This is therefore equal to $2\pi(hx/a + ky/b)$ radians and it represents the phase of scattering from the point T compared with zero phase at the origin of the cell.

When this calculation is extended to three dimensions, the intercept of the plane hkl with the crystallographic z axis at the point c/l and the projection of z on the perpendicular from O to the plane must also be taken into consideration. The phase of scattering by an atom at the point x, y, z is then given by

$\begin{displaymath} 2\pi\left({hx\over a} + {kx\over b} + {lz\over c}\right) \mathrm{ radians.}\end{displaymath}$

This is therefore the expression for the calculated phase angle $\phi_j$ for use in equations such as (3) and (4). The amplitude f_j for the scattering of the atom, which takes account of the number of electrons in the atom and the fact that they are not actually concentrated at the point x, y, z but distributed round it, is the atomic scattering factor f, already discussed. The equations for the real part (A') and the imaginary part (B') of the structure factor, corresponding to equations (3) and (4) are therefore:

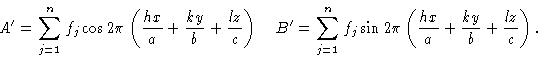
$\begin{displaymath} A'=\sum_{j=1}^n f_j \cos2\pi\left({hx\over a} + {kx\over b} ... ...j \sin2\pi\left({hx\over a} + {kx\over b} + {lz\over c}\right).\end{displaymath}$

Or, in exponential form, the structure factor may be expressed as:

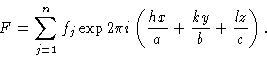
$\begin{displaymath} F=\sum_{j=1}^n f_j \exp2\pi i\left({hx\over a} + {kx\over b} + {lz\over c}\right).\end{displaymath}$

In each case the summation is taken over the n atoms in the unit cell.

In practice, any one atom in the unit cell is related to other atoms in the cell by the operation of the various symmetry elements. By taking account of the relationship between the coordinates of these symmetry-related atoms, formulae can be derived expressing the sum of the $\cos \phi_j$ factors and the sum of the $\sin \phi_j$ factors for the whole of this group of symmetry related atoms. These sums are usually called A and B respectively. The whole sum, A or B, is then multiplied by the atomic scattering factor which again, in practice, is corrected for thermal motion of the atoms which further smears out the electron cloud and causes a more rapid drop in f_j with $\sin \theta/\lambda$ than that illustrated in Fig. 5. Then:

$\begin{displaymath} A'=\sum f_j A \quad\mathrm{and}\quad B'=\sum f_j B,\end{displaymath}$

where the sum is taken over the atoms of one asymmetric unit only. The details of these extensions to the basic principles of the calculation of structure factors are outside the scope of this pamphlet but formulae for A and B are given in the International Tables for X-ray Crystallography , Volume 1, 1969, (Birmingham, Kynoch Press). The calculations are usually carried out on a computer.

Finally it should be mentioned that whenever a collection of atoms for which a structure-factor calculation is being performed has a centre of symmetry, the resultant structure factor is always entirely real and hence the associated phase angles are always either 0 or $\pi$ . That this is so may easily be seen by dividing the structure up into centrosymmetrically related pairs. For every atom at x, y, z, there will be one at -x, -y, -z and hence the imaginary parts, B', of the structure factor, since they involve a sine term, will be opposite in sign and cancel out.

Crystallography Matters!

Introduction to the calculation of structure factors

S. C. Wallwork