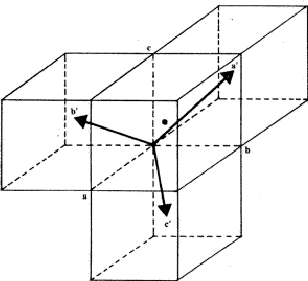
The reciprocal lattice

A. Authier

1. Introduction

The fundamental property of a crystal is its triple periodicity and a crystal may be generated by repeating a certain unit of pattern through the translations of a certain lattice called the direct lattice. The macroscopic geometric properties of a crystal are a direct consequence of the existence of this lattice on a microscopic scale. Let us for instance consider the natural faces of a crystal. These faces are parallel to sets of lattice planes. The lateral extension of these faces depends on the local physico-chemical conditions during growth but not on the geometric properties of the lattice. To describe the morphology of a crystal, the simplest way is to associate, with each set of lattice planes parallel to a natural face, a vector drawn from a given origin and normal to the corresponding lattice planes. To complete the description it suffices to give to each vector a length directly related to the spacing of the lattice planes. As we shall see in the next section this polar diagram is the geometric basis for the reciprocal lattice .

On the other hand, the basic tool to study a crystal is the diffraction of a wave with a wavelength of the same order of magnitude as that of the lattice spacings. The nature of the diffraction pattern is governed by the triple periodicity and the positions of the diffraction spots depend directly on the properties of the lattice. This operation transforms the direct space into an associated space, the reciprocal space , and we shall see that the diffraction spots of a crystal are associated with the nodes of its reciprocal lattice.

The reciprocal lattice is therefore an essential concept for the study of crystal lattices and their diffraction properties. This concept and the relation of the direct and reciprocal lattices through the Fourier transform was first introduced in crystallography by P. P. Ewald (1921).

2. Crystallographic definition

2.1 Definition

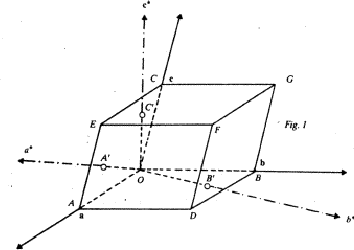
Let a, b, c be the basic vectors defining the unit cell of the direct lattice. The basic vectors of the reciprocal lattice are defined by:

$\begin{displaymath} \textbf{a*} = \frac{(\textbf{b} \wedge \textbf{c})}{(\textbf... ...c*} = \frac{(\textbf{a} \wedge \textbf{b})}{\textbf{(a, b, c)}}\end{displaymath}$

(2.1)

The modulus of a* is equal to the ratio of the area of the face OBCG opposite to a to the volume of the cell built on the three vectors a, b, c. Referring to Fig. 1, we may write:

$\begin{displaymath} \textbf{a*} = 1/OA^{\prime} \quad \textbf{b*} = 1/OB^{\prime} \quad \textbf{c*} = 1/OC^{\prime}\end{displaymath}$

(2.2)

$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

From the definition of the reciprocal lattice vectors, we may therefore already draw the following conclusions:

(i) Each of the three vectors a*, b*, c* is normal to a set of lattice planes of the direct lattice (b, c; c, b; a, b) and their moduli are respectively equal to the inverse of the spacings of these three sets of lattice planes. The basic vectors of the reciprocal lattice possess therefore the properties that we were looking for in the introduction. We shall see in the next section that with each family of lattice planes of the direct lattice a reciprocal lattice vector may be thus associated.

(ii) The dimensions of the moduli of the reciprocal lattice vectors are those of the inverse of a length. For practical purposes the definition equations (2.1) may be rewritten after the introduction of a scale factor $\sigma$ which has the dimension of an area:

$\begin{displaymath} \textbf{a*} = \frac{(\textbf{b} \wedge \textbf{c})}{(\textbf{a, b, c})} \sigma\end{displaymath}$

(2.3)

This is only done to give the reciprocal lattice vector the dimension of length when one wants to actually draw the reciprocal lattice and we shall not make use of this scale factor in this paper.

From relations 2.1 it can readily be shown that the two sets of basic vectors satisfy the following equations:

$\begin{displaymath} \textbf{a}\cdot\textbf{a*} = 1\quad etc\dots \qquad \textbf{a}\cdot\textbf{b*} = 0 \quad etc\dots\end{displaymath}$

(2.4)

The two sets of equations (2.1) and (2.4) are equivalent and equations (2.4) are sometimes used as the definition equations of the reciprocal lattice. These relations are symmetrical and show that the reciprocal lattice of the reciprocal lattice is the direct lattice.

2.2 Fundamental law of the reciprocal lattice

(a) with each node of the reciprocal lattice whose numerical coordinates have no common divider can be associated a set of direct lattice planes

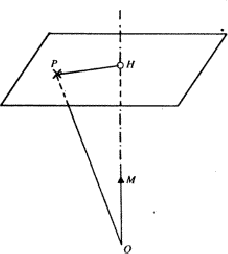
Let M be a reciprocal lattice point whose coordinates h, k, l have no common divider (M is the first node on the reciprocal lattice row OM), and P a point in direct space. We may write:

$\begin{displaymath} \textbf{OM} = h\textbf{a*} + k\textbf{b*} + l\textbf{c*} \quad \textbf{OP} = x\textbf{a} + y\textbf{b} + z\textbf{c} \end{displaymath}$

(2.5)

Let us look for the locus of all points P of direct space such that the scalar product $\textbf{OP} \cdot \textbf{OM}$ should be constant. It is a plane normal to O and passes through the projection H of P on OM (Fig. 2). Using 2.4, we find easily that the equation of this plane in direct space is given by

$\begin{displaymath} \textbf{OP} \cdot \textbf{OM} = \textbf{OH} \cdot \textbf{OM} = hx + ky + lz = C\end{displaymath}$

(2.6)

Let us now assume that P is a node of the direct lattice:

$\begin{displaymath} \textbf{OP} = u\textbf{a} + v\textbf{b} + w\textbf{c}\quad (u, v, w \hbox{ integers})\end{displaymath}$

The locus of P is a lattice plane of the direct lattice. Its equation is:

$\begin{displaymath} \textbf{OH} \cdot \textbf{OM} = hu + kv + lw = C\end{displaymath}$

(2.7)

**Figure 1:**
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

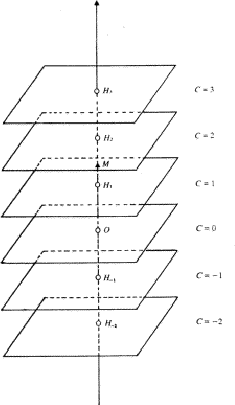
Since all numbers in the left hand side are integers, we find that C is also an integer. With each value of C we may associate a lattice plane and thus generate a set of direct lattice planes which are all normal to the reciprocal vector OM (Fig. 3). The distance of one of these planes to the origin is given by:

$\begin{displaymath} OH = C/OM \quad (C = -2, -1, 0, 1, 2, 3, \dots)\end{displaymath}$

If OH₁ is the distance of the first plane to the origin, we may write:

$\begin{displaymath} OH = C \times OH_1\end{displaymath}$

The lattice planes have, as expected, an equal spacing:

$\begin{displaymath} d_{hkl} = OH_1 = 1/OM = 1/{\cal{N}}_{hkl}\end{displaymath}$

(2.8)

where $\cal{N}_{hkl}$ is the parameter along the reciprocal lattice row OM. Equation 2.8 may be rewritten:

$\begin{displaymath} d_{hkl} \cdot {\cal{N}}_{hkl} = 1\end{displaymath}$

(2.9)

This is the fundamental relation of the reciprocal lattice which shows that with any node M of the reciprocal lattice whose numerical coordinates have no common divider we may associate a set of direct lattice planes normal to OM. Their spacing is inversely proportional to the parameter along the reciprocal row OM.

In order that the correspondence between direct and reciprocal lattice should be fully established, the converse of the preceding theorem should also be demonstrated. This will be done in paragraph 2.2(c).

**Figure 2:**
$\begin{figure} \includegraphics {fig3.ps} \end{figure}$

It is interesting at this point to give an interpretation to the reciprocal lattice points whose numerical coordinates have a common divider. Let us consider such a point for which:

$\begin{displaymath} \textbf{OM} = h\textbf{a*} + k\textbf{b*} + l\textbf{c**}\end{displaymath}$

where

$\begin{displaymath} h = nh_1; \quad k = nk_1: \quad l = nl_1\end{displaymath}$

h₁, k₁, l₁, have no common divider. We may write:

$\begin{displaymath} \textbf{OM} = n\textbf{OM}_1\end{displaymath}$

where M₁ is the first node on the reciprocal lattice row OM.

Let d_h₁k₁l₁ be the spacing of the direct lattice planes associated with M. The fundamental law of the reciprocal lattice may be written:

$\begin{displaymath} d_{h_1k_1l_1} \cdot {\cal{N}}_{h_1k_1l_1} = 1\end{displaymath}$

We may also write:

$\begin{displaymath} \frac{1}{n}d_{h_1k_1l_1} \cdot n{\cal{N}}_{h_1k_1l_1} = 1\end{displaymath}$

(2.10)

$\begin{displaymath} \frac{1}{n}d_{h_1k_1l_1} \cdot OM = 1\end{displaymath}$

In other words, with the reciprocal lattice node M may be associated a set of fictitious planes in direct space whose spacing is n times smaller than the real lattice spacing. We shall see that in diffraction by crystal lattices a reciprocal lattice point may be associated with each Bragg diffraction: if the coordinates of this point have no common divider, Bragg's law is satisfied to the first order (2d sin $\theta$ = $\lambda$ ); if they have a common divider, n, Bragg's law is satisfied to the nth order (2d sin $\theta$ = n $\lambda$ ), one may also say it is satisfied to the first order for the fictitious lattice planes of spacing d/n (2d/n sin $\theta$ = $\lambda$ ) and this is what is actually always done in practice.

(b) Miller indices

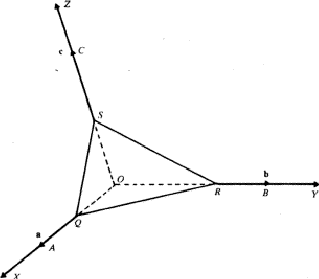
Let us consider one particular lattice plane of equation

hx + ky + lz = C

and let Q, R and S be its intersections with the three axes, respectively (Fig. 4); we have:

$\begin{displaymath} x = C/h; \quad OQ = a \cdot C/h \qquad y = C/k; \quad OR = b \cdot C/k \qquad z = C/l; \quad OS = c \cdot C/l\end{displaymath}$

We conclude that the lattice plane intercepts, along the three axes, lengths which are inversely proportional to three integers which have no common divider. This is the so-called Law of Rational Indices or Hauy Law. The three indices are called the Miller indices.

The planes which are crystallographically the most important ones are the densest ones, that is those with the largest spacing. Equation (2.9) tells us that they are associated with the shortest vectors in reciprocal lattice and that their Miller indices are therefore small. This is the reason why Hauy's law was also called the law of simple rational indices.

Let us consider a set of direct lattice planes of equation:

hx + ky + lz = C

Since x, y, z may be integers, h, k, and l are also integers. If C = 1, corresponding to the first plane in the family, h, k and l have no common divider. Let us now consider the reciprocal lattice vector

$\begin{displaymath} \textbf{ON}_{hkl} = h\textbf{a*} + k\textbf{b*} + l\textbf{c*}\end{displaymath}$

Its scalar products with the vectors QR and RS (Fig. 4) are respectively equal to:

$\begin{displaymath} \textbf{ON}_{hkl}\cdot \textbf{QR} = (h\textbf{a*} + k\textb... ...\textbf{C}}{k}\textbf{b}- \frac{\textbf{C}}{h}\textbf{a}\right)\end{displaymath}$

$\begin{displaymath} \textbf{ON}_{hkl}\cdot \textbf{RS} = (h\textbf{a*} + k\textb... ...\textbf{C}}{l}\textbf{c}- \frac{\textbf{C}}{k}\textbf{b}\right)\end{displaymath}$

They are both equal to zero, which shows that the reciprocal lattice vector is normal to the set of direct lattice planes; the scalar product of ON_hkl by OP where P is any direct lattice node in a plane of the set can be written in the form of equation (2.6). The reciprocal theorem is thus demonstrated.

**Figure 3:**
$\begin{figure} \includegraphics {fig4.ps} \end{figure}$

3. Reciprocal space and dual space

3.1 Definition

Let us now call e_i the basic vectors of a vectorial space and xⁱ the coordinates of a given vector x. We may write:

$\begin{displaymath} \textbf{x} = x^i\textbf{e}_i = x^1\textbf{e}_1+x^2\textbf{e}_2+x^3\textbf{e}_3\end{displaymath}$

(3.1)

using Einstein's summation convention. A change of coordinates may be described by the following relations:

$\begin{displaymath} \textbf{e}^{\prime}_i = A^i_j\textbf{e}_j; \quad \textbf{e}_... ... \qquad x^{\prime i} = B^i_jx^i; \quad x^i = A^i_j x^{\prime j}\end{displaymath}$	(3.2)
$\begin{displaymath} A^i_jB^j_k = \delta^i_k \qquad (\delta = 1 \hbox{ if } i = k; \quad \delta = 0 \hbox{ if } i \neq k)\end{displaymath}$

Quantities with a subscript transform in a change of coordinate like the basic vectors and are called covariant ; those with a superscript transform like the coordinates and are called countervariant . Let us now consider the scalar products:

$\begin{displaymath} x_i = \textbf{x} \cdot \textbf{e}_i = x^j\textbf{e}_i \cdot \textbf{e}_j = x^jg_{ij}\end{displaymath}$

(3.3)

where we put

$\begin{displaymath} g_{ij} = \textbf{e}_i \cdot \textbf{e}_j \end{displaymath}$

(3.4)

The nine quantities g_ij are the components of the so-called metric tensor. We shall show that the three quantities x_i are the covariant coordinates of x. The system of equations (3.3) expresses the x_i in terms of the xⁱ. We can resolve this system and write

xⁱ = x_jg^ij

(3.5)

where

$\begin{displaymath} g^{ij}g_{jk} = \delta^i_k \end{displaymath}$

(3.6)

This can always be written since the determinant built on the g_ij is different from zero by definition of the scalar product.

Let us now introduce the following set of vectors

$\begin{displaymath} \textbf{e}^i = g^{ij}\textbf{e}_j \end{displaymath}$

(3.7)

This set of vectors constitutes a set of basic vectors. To show this we may simply transform equation (3.1):

$\begin{displaymath} \textbf{x} = x^i\textbf{e}_i = x_jg^{ij}\textbf{e}_j = x_j\textbf{e}^j\end{displaymath}$

(3.8)

The vectors e^j constitute therefore a set of basic vectors and the x_j are the coordinates of x with respect to this base. They are called countervariant basic vectors. They are also identical to the basic vectors of the reciprocal space. This can easily be demonstrated by showing that they satisfy the basic relations (2.3) of the reciprocal space vectors. Let us consider the scalar products $\textbf{e}_i \cdot\textbf{e}^j$ .Using (3.7), (3.4) and (3.6), we may write:

$\begin{displaymath} \textbf{e}_i \cdot \textbf{e}^j = g^{ik} \textbf{e}_i \cdot \textbf{e}_k = g^{jk}g_{ik} = \delta^j_i\end{displaymath}$

which is indeed identical to 2.3.

3.2 The volumes of the unit cells in direct and reciprocal space are inverse

Let V be the volume of the unit cell. In a change of coordinate:

$\begin{displaymath} \textbf{e}_i \times \textbf{e}^{\prime}_j B^j_i \end{displaymath}$

(3.9)

we have

$\begin{displaymath} V = V^{\prime}\Delta(B)\end{displaymath}$

where $\Delta(B)$ is the determinant built on B^j_i. In the same way, we may write:

$\begin{displaymath} {\Delta}g_{ij} = {\Delta}g^{\prime}_{ij}{\Delta}\end{displaymath}$

(3.10)

Let us now assume that the base e_j is orthonormal. There comes:

$\begin{displaymath} V = {\Delta}(B), \quad {\Delta}g_{ij} = {\Delta}(B)^2 \end{displaymath}$

(3.11)

We have then demonstrated the following general result:

$\begin{displaymath} {\Delta}g_{ij} = V^2 \end{displaymath}$

(3.12)

From (3.6) we know that

$\begin{displaymath} {\Delta}g_{ij} \cdot {\Delta}g^{ij} = 1\end{displaymath}$

(3.13)

It is easy to show the following relation, equivalent to (3.12):

$\begin{displaymath} {\Delta}g^{ij} = V^{*2}\end{displaymath}$

(3.14)

where V^* is the volume of the unit cell in reciprocal space.

From (3.12), (3.13) and (3.14), we obtain finally:

$\begin{displaymath} V \cdot V^* = 1\end{displaymath}$

3.3 Calculation of the reciprocal lattice vectors using the metric tensor

Relation (3.7) is the most convenient one to use to compute the reciprocal lattice parameters or any quantity related to them. Let a, b, c and $\alpha, \beta, \gamma$ be the direct lattice parameters. The doubly covariant coefficients of the metric tensor are then:

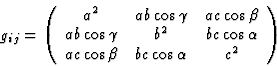$\begin{displaymath} g_{ij} = \left(\begin{array} {ccc} a^2 & ab\cos\gamma & ac \... ...os\alpha \\ ac\cos\beta & bc\cos\alpha & c^2\end{array} \right)\end{displaymath}$

(3.15)

Its determinant, that is the square of the volume of the direct lattice unit cell is equal to:

$\begin{displaymath} V^2 = a^2b^2c^2(1+2 \cos \alpha \cos \beta \cos \gamma - \cos^2 \alpha - \cos^2 \beta - \cos^2 \gamma)\end{displaymath}$

(3.16)

By inversing 3.15 we obtain the doubly contravariant of the metric tensor, g^ij

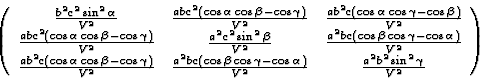$\begin{displaymath} \left(\begin{array} {ccc} \frac{b^2c^2 \sin^2 \alpha}{V^2} &... ...alpha)}{V^2}&\frac{a^2b^2\sin^2 \gamma}{V^2}\end{array} \right)\end{displaymath}$

(3.17)

Using (3.17), we can easily obtain the following relations:

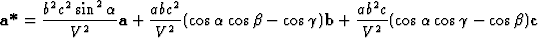
$\begin{displaymath} \textbf{a*} = \frac{b^2c^2 \sin^2 \alpha}{V^2} \textbf{a}+\f... ... - \cos \beta) \textbf{c}\end{displaymath}$

$\begin{displaymath} a* = \frac{bc \sin \alpha}{V}\end{displaymath}$

(3.18)

$\begin{displaymath} \cos \gamma* = \frac{\cos \alpha \cos \beta - \cos \gamma}{\left\vert\sin \alpha \sin \beta \right\vert}\end{displaymath}$

4. Crystallographic calculations using the reciprocal lattice

4.1 Scalar product of direct and reciprocal lattice vectors

Let us consider a direct lattice vector

$\begin{displaymath} u\textbf{a} + v\textbf{b} + w\textbf{c}\end{displaymath}$

and a reciprocal lattice vector

$\begin{displaymath} h\textbf{a*} + k\textbf{b*} + l\textbf{c*}\end{displaymath}$

Using (2.3), their scalar product is equal to:

hu + kv + lw

4.2 Vector product of two direct lattice vectors

Let us consider two direct lattice vectors:

$\begin{displaymath} \textbf{n}_1 = u_1\textbf{a}+ v_1 \textbf{b} + w_1 \textbf{c... ... \textbf{n}_2 = u_2\textbf{a} + v_2 \textbf{b} + w_2 \textbf{c}\end{displaymath}$

Their vector product is equal to:

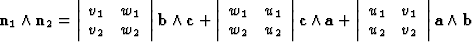
$\begin{displaymath} \textbf{n}_1 \wedge \textbf{n}_2 = \left\vert\begin{array} {... ...\ u_2 & v_2\end{array} \right\vert \textbf{a} \wedge \textbf{b}\end{displaymath}$

Using the definition (2.1) of the basic reciprocal vectors, we may write:

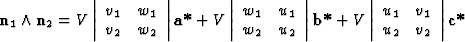$\begin{displaymath} \textbf{n}_1 \wedge \textbf{n}_2 = V \left\vert\begin{array}... ... {cc} u_1 & v_1 \\ u_2 & v_2\end{array} \right\vert \textbf{c*}\end{displaymath}$

(4.1)

This shows that the vector product of two direct lattice vectors is easily expressed in terms of the basic reciprocal vectors.

4.3 Indices of the set of lattice planes parallel to two direct lattice rows

The vector product of two vectors n₁ and n₂ respectively parallel to these two rows is normal to the set of lattice planes and is therefore parallel to the reciprocal lattice vector associated with the lattice planes. If h, k, l are its indices, we may therefore write:

$\begin{displaymath} \frac{h}{v_1w_2-v_2w_1} = \frac{k}{w_1u_2-w_2u_1}=\frac{l}{u_1v_2-u_2v_1}\end{displaymath}$

(4.2)

4.4 Zone axis of two sets of direct lattice planes

Let h₁, k₁, l₁ and h₂, k₂, l₂ be the Miller indices of the two sets of direct lattice planes. The vector product of the two reciprocal lattice vectors associated with them is necessarily parallel to their zone axis. The coordinates of this zone axis are therefore given by:

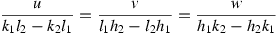$\begin{displaymath} \frac{u}{k_1l_2-k_2l_1} = \frac{v}{l_1h_2-l_2h_1} = \frac{w}{h_1l_2-h_2l_1}\end{displaymath}$

(4.3)

4.5 Reciprocity of F and I lattices

Let us consider a face-centered lattice. It is well known that the basic vectors a $^{\prime}$ , b $^{\prime}$ , c $^{\prime}$ , of the elementary cell are given in terms of the vectors a, b, c of the face centered cell by (Fig. 5):

$\begin{displaymath} \textbf{a}^{\prime} = \frac{\textbf{b}+\textbf{c}}{2} \quad ... ...{2} \quad \textbf{c}^{\prime} = \frac{\textbf{a}+\textbf{b}}{2}\end{displaymath}$

(4.4)

In a similar way, the basic vectors a $^{\prime\prime}$ ,b $^{\prime\prime}$ , c $^{\prime\prime}$ of the elementary cell of a body centered lattice are given in terms of the basic vectors of the multiple cell by (Fig. 6):

$\begin{displaymath} \textbf{a}^{\prime\prime} = \frac{-\textbf{a}+\textbf{b}+\te... ...{c}^{\prime\prime} = \frac{\textbf{a}+\textbf{b}-\textbf{c}}{2}\end{displaymath}$

(4.5)

Let us now look for the reciprocal lattice of the face-centered lattice. Its unit cell vectors are given by, using (2.1) and (4.4):

$\begin{displaymath} \textbf{a}^{\prime*} = \left(\frac{(\textbf{a}+\textbf{c})}{... ...(\textbf{a}^{\prime}, \textbf{b}^{\prime}, \textbf{c}^{\prime})\end{displaymath}$

(4.6)

**Figure 4:**
$\begin{figure} \includegraphics {fig5.ps} \end{figure}$

**Figure 5:**
$\begin{figure} \includegraphics {fig6.ps} \end{figure}$

Noting that the face-centered cell is of the fourth order, we find:

$\begin{displaymath} \textbf{a}^{\prime*} = \frac{\textbf{c} \wedge \textbf{b}}{(... ...{a,b,c})}+\frac{\textbf{a} \wedge \textbf{b}}{(\textbf{a,b,c})}\end{displaymath}$

We may thus express a $^{\prime}$ * in terms of the basic vectors of the reciprocal lattice of the lattice of vectors a, b, c:

$\begin{displaymath} \textbf{a}^{\prime*} = -\textbf{a}^* + \textbf{b}^* + \textbf{c}^*\end{displaymath}$

This may also be written:

$\begin{displaymath} \textbf{a}^{\prime*} = \frac{-(2\textbf{a}^*)+(2\textbf{b}^*)+(2\textbf{c}^*)}{2}\end{displaymath}$

This relation shows that the reciprocal lattice of a face-centered lattice is a body centered lattice whose multiple cell is defined by 2a*, 2b*, 2c*. If we index the reciprocal lattice defined by a*, b*, c*, that is the reciprocal lattice of the multiple lattice defined by a, b, c, we find that only the nodes such that

$\begin{displaymath} h + k = 2n \quad k + l = 2n^{\prime} \quad l + h = 2n^{\prime\prime}\end{displaymath}$

belong to the reciprocal lattice of the face-centered lattice. This shows that the only Bragg reflexions on a face-centered lattice have indices which are all of the same parity.

5. Diffraction condition in the reciprocal lattice

Let us consider a plane monochromatic wave incident on a crystal and let k_o = s $_o/\lambda$ be its wave vector. Each scatterer will diffuse this wave in every direction with the same wavelength (coherent scattering). The total amplitude scattered in a particular direction s_h will be obtained by summing the amplitudes scattered in this particular direction by all scatterers, taking into account their phase relations. Let A and B be two homologous points in the structure, that is AB = r is a direct lattice vector. The phase differences between the waves scattered by A and B is equal to:

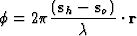$\begin{displaymath} \phi = 2\pi \frac{(\textbf{s}_h - \textbf{s}_o)}{\lambda}\cdot \textbf{r}\end{displaymath}$

(5.1)

(s_h and s_o are unit vectors in the reflected and incident directions, respectively).

There will be diffraction of the incident wave by the crystal if the wavelets diffracted by all homologous points are in phase, that is if $\phi$ is equal to an integer times 2 $\pi$ whatever the direct lattice vector r. The phase $\phi$ may also be written:

$\begin{displaymath} \phi = 2 \pi \textbf{R} \cdot \textbf{r}\end{displaymath}$

(5.2)

where R = (s_h - s_o)/ $\lambda$ is the so-called diffusion vector.

The modulus of the diffusion vector has the dimension of the reciprocal of a length. R can therefore be expanded in reciprocal space:

$\begin{displaymath} \textbf{R} = h\textbf{a*} + k\textbf{b*} + l\textbf{c*}\end{displaymath}$

The position vector r can in the same way be expressed in terms of its coordinates u, v, w in direct space. Applying relations (2.3), we may therefore write the phase difference $\phi$ in the following way:

$\begin{displaymath} \phi = 2 \pi (hu + kv + lw)\end{displaymath}$

(5.3)

We may note that u, v, w being the coordinates of a direct lattice vector are integers. If $\phi$ is to be equal to an integer times 2 $\pi$ whatever u, v, w, we conclude that h, k, l are necessarily also equal to integers; in other words, the diffusion vector is a reciprocal lattice vector . This is the diffraction condition in reciprocal space. Bragg's law and the Ewald sphere construction are easily deduced from this result.

Let O be the origin of the reciprocal lattice and IO and IH vectors respectively equal to s $_o/\lambda$ and s $_h/\lambda$ .The vector OH is therefore equal to R (Fig. 7). If the diffraction condition is satisfied, H is a reciprocal lattice node. We have therefore the following construction: we draw through O a line parallel to the incident direction, let $IO = 1/\lambda$ , then draw a sphere centered in I with radius 1/ $\lambda$ . If it passes through another reciprocal lattice node H, there is a reflected beam parallel to IH.

We may notice in the triangle IOH that OH/2 = IH $\times$ sin $\theta$ ,calling $\theta$ the angle between IO or IH with the bissectrix of OIH, that is with the trace of the set of direct lattice planes associated with the node H.

We know from (2.8) that

$\begin{displaymath} OH = \frac{n}{d}\end{displaymath}$

where d is the lattice spacing of the direct lattice planes and n the order of H along the reciprocal lattice row OH. We find thus that:

$\begin{displaymath} \frac{n}{2d} = \frac{\sin \theta}{\lambda}\end{displaymath}$

which is of course Bragg's law.

A reciprocal lattice node may thus be associated with each Bragg reflection .

This result can also be obtained directly through the properties of Fourier transforms. The basic assumption of the geometrical theory of diffraction is that the amplitude of the incident wave at each scatterer is constant. This assumption is acceptable if the interaction between the incident wave and the scatterers is small enough. The total diffracted amplitude in a given direction is therefore simply equal to the sum of the amplitudes scattered in this direction by every scatterer, taking into account their phase relationships. It is equal to:

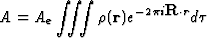$\begin{displaymath} A = A_e \int\int\int \rho(\textbf{r})e^{-2{\pi}i\textbf{R}{\cdot}r}d{\tau}\end{displaymath}$

(5.4)

using (5.1) and (5.2). A_e is the amplitude diffracted by one scatterer and $\rho$ (r) the density of scatterers electrons if we consider X-ray diffraction for instance. The integral is extended over the volume of the crystal. We shall assume it here to be infinite. Expression (5.4) shows that the distribution of diffracted amplitudes is the Fourier transform of the electron density $\rho$ (r). If the diffracting medium is crystalline, it is triply periodic. The Fourier transform of $\rho$ (r) is then a distribution of Dirac masses at each reciprocal lattice node. The weight associated with each one of them is equal to the structure factor:

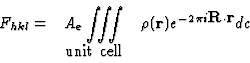
$\begin{displaymath} \begin{array} {rcl} F_{hkl} = & A_e \displaystyle \int\!\!\!... ...xtbf{R}{\cdot}\textbf{r}}dc \\ & \hbox{unit cell} &\end{array}\end{displaymath}$

(5.5)

$\begin{displaymath} = \sum_j f_je^{-2{\pi}i}(hx_j + ky_j + lz_j)\end{displaymath}$

where f_j is the form factor of atom j and x_j, y_j, z_j its numerical coordinates in the unit cell.

...by:: In this article the symbol 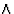is used to represent a vector product and commas (e.g. a, b, c) to represent the triple product [which in this case is the volume of the unit cell].

Crystallography Matters!