Crystal structure analysis using the 'superposition' - and 'complementary' - structures
Ernst Höhne and Leo Kutschabsky
1. General
Quite a number of crystal structures contain parts (e.g. heavy atoms or building units) with a higher symmetry (e.g. with additional translation or pseudotranslation) compared with the whole structure. In those cases, standard methods may not lead to correct results, this is why special methods may have to be applied.
As an example let the heavy atoms (strongly reflecting atoms) have parameters xs, ys, zs and xs, ys, ![]() + zs (Fig. 1). Then they contribute only to the structure factors F(hkl) with l = 2n, since their contribution Fs(hkl) is equal to
+ zs (Fig. 1). Then they contribute only to the structure factors F(hkl) with l = 2n, since their contribution Fs(hkl) is equal to
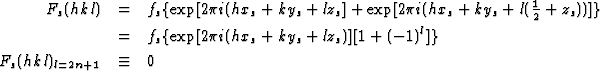 |
(1.1) |
Therefore the |F(hkl)|2 with l = 2n are systematically strong, compared with those with l = 2n + 1, i.e. for the mean values ![]() of the intensities within any region of
of the intensities within any region of ![]() values
values
![]()
 |
If such a systematic distribution of the intensities or a similar one occurs, it is useful, for methodical reasons, to regard the electron density ![]() as the sum of two - or if necessary - of several parts.
as the sum of two - or if necessary - of several parts.
Thus the electron density function
![]()
may for the case indicated in Fig. 1 be written
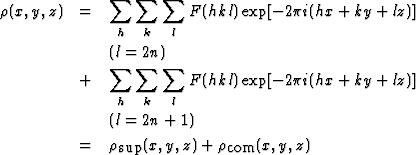 |
(1.2) |
| (1.2') |
where
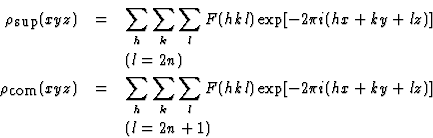 |
![]() denotes a hypothetical structure, called the superposition structure, which is related to the real structure in the following way
denotes a hypothetical structure, called the superposition structure, which is related to the real structure in the following way
![\begin{displaymath} \textstyle{\rho}_{\mbox{sup}}(x, y, z) = \frac{1}{2}[{\rho}(x, y, z) + {\rho}(x, y, \frac{1}{2} + z)]\end{displaymath}](https://www.iucr.org/__data/assets/image/0012/13350/img12.gif) |
(1.3) |
In ![]() (Fig. 2) the two heavy atoms (
(Fig. 2) the two heavy atoms ( ) appear with correct weights because they are connected by a translation of c/2, whereas the remaining atoms (squares and triangles) appear with half their weights (marked by shaded symbols) at the original position and at a second point shifted relative to it by c/2.
) appear with correct weights because they are connected by a translation of c/2, whereas the remaining atoms (squares and triangles) appear with half their weights (marked by shaded symbols) at the original position and at a second point shifted relative to it by c/2.
 |
Generally speaking, the symmetry of ![]() is identical with the symmetry of the arrangement of the heavy atoms (or other building units with higher symmetry) taken by themselves. This higher symmetry may either be strictly true for the heavy atoms taken by themselves, or only in approximation. In the latter case it may be useful to disregard deviations from the higher symmetry, to start with.
is identical with the symmetry of the arrangement of the heavy atoms (or other building units with higher symmetry) taken by themselves. This higher symmetry may either be strictly true for the heavy atoms taken by themselves, or only in approximation. In the latter case it may be useful to disregard deviations from the higher symmetry, to start with.
The symmetry of the complementary structure ![]() follows from (1.2) and (1.3):
follows from (1.2) and (1.3):
![\begin{displaymath} \textstyle{\rho}_{\mbox{com}}(x, z, y) = \frac{1}{2}[{\rho}(x, y, z) - {\rho}(x, y, \frac{1}{2} + z)]\end{displaymath}](https://www.iucr.org/__data/assets/image/0016/13363/img18.gif) |
(1.4) |
Its properties are shown in Fig. 3. Accordingly, the heavy atoms (i.e. those which occur in pairs related to a shift of c/2) are absent in ![]() , whereas any other atom appears with half its weight at its real position and with half negative weight at a position shifted by c/2 (Fig. 3). The space group symmetry of the arrangement with positive weights in
, whereas any other atom appears with half its weight at its real position and with half negative weight at a position shifted by c/2 (Fig. 3). The space group symmetry of the arrangement with positive weights in ![]() is identical with the space group of the real structure
is identical with the space group of the real structure ![]() . In a similar way, the introduction of a superposition and a complementary structure may be indicated by systematically strong reflections occurring, e.g. for h = 2n or h + k = 2n or h + k + l = 2n etc.
. In a similar way, the introduction of a superposition and a complementary structure may be indicated by systematically strong reflections occurring, e.g. for h = 2n or h + k = 2n or h + k + l = 2n etc.
 |
If, on the other hand, the heavy atoms (or another part of the structure, taken by itself) possesses a higher symmetry (other than translation) than the structure as a whole, the introduction of other kinds of hypothetical structures, also to be called ![]() and
and ![]() may be of use. In this case, no systematically strong and weak reflections result.
may be of use. In this case, no systematically strong and weak reflections result.
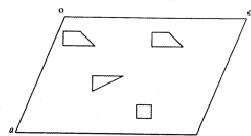
As an example, we consider a structure in ![]() containing two heavy atoms of the same element per unit cell. The heavy atoms considered by themselves are connected by a centre of symmetry. The structure computed with phases (signs) taken from the heavy atom contribution is necessarily centrosymmetric and is related to the real structure by its superposition with its centrosymmetric image (Fig. 4). If referred to such a partial centre of symmetry as origin, the electron density distribution of the superposition structure
containing two heavy atoms of the same element per unit cell. The heavy atoms considered by themselves are connected by a centre of symmetry. The structure computed with phases (signs) taken from the heavy atom contribution is necessarily centrosymmetric and is related to the real structure by its superposition with its centrosymmetric image (Fig. 4). If referred to such a partial centre of symmetry as origin, the electron density distribution of the superposition structure ![]() may be expressed as
may be expressed as
![\begin{displaymath} \textstyle{\rho}_{\mbox{sup}}(x, y, z) = \frac{1}{2}[{\rho}(x, y, z) + {\rho}(\overline{x}, \overline{y}, \overline{z})]\end{displaymath}](https://www.iucr.org/__data/assets/image/0014/13370/img24.gif) |
(1.5) |
The real structure or at least part of it may in many cases of this kind be obtained using well established chemical knowledge, such as atomic distances, known stereochemistry of molecules or parts of them as of coordination polyhedra etc.
 |
2. Special methods
2.1 Linear structure factor equations
In many cases two coordinates (e.g. xj, yj) of any atom in the real structure are the same as those of the superposition structure. There arises the task of determining the third atomic coordinate (zj). The method of linear structure factor equations (SFE) by Kutschabsky2 and by Kutschabsky and Höhne3 allows us to calculate these atomic coordinates (zj) directly, using the reflection of the first level of the reciprocal lattice (F(hkl)).
The basic relation follows directly from the formula for the structure factor
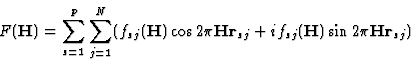 |
(2.1) |
where P is the number of equipoints in the unit cell, N is the number of symmetrically independent atoms, fsj is the atomic scattering factor and ![]() is the radius vector of the centre of atom s, j.
is the radius vector of the centre of atom s, j.
Vector ![]() is defined by
is defined by ![]() * +
* + ![]() * +
* + ![]() *, where (
*, where (![]() *,
*, ![]() *,
*, ![]() *) are the basic reciprocal vectors.
*) are the basic reciprocal vectors.
Using the symmetry matrices Rs and the translation ts we obtain:
![\begin{displaymath} F(H) = \sum^p_{s = 1} \sum^N_{j = 1} f_{sj}(\textbf{H})[\cos... ...\textbf{t}_s) + i \sin 2{\pi}H(R_s\textbf{r}_j + \textbf{t}_s)]\end{displaymath}](https://www.iucr.org/__data/assets/image/0017/13382/img35.gif) |
(2.2) |
The separation into the components leads to
![\begin{displaymath} F(H) = \sum^p_{s = 1} \sum^N_{j = 1} {\gamma}_{sj}(\textbf{H... ...pi}({\alpha}_sx_j + {\beta}_sy_j + {\gamma}_sz_j + {\delta}_s)]\end{displaymath}](https://www.iucr.org/__data/assets/image/0018/13383/img36.gif) |
(2.3) |
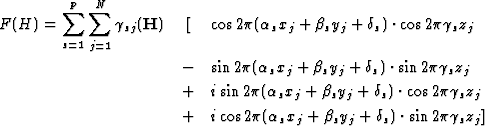 |
(2.4) |
In the most important cases the factor ![]() depends only on l (not h or k). In those cases we obtain for structure factors P(hkl) with constant L
depends only on l (not h or k). In those cases we obtain for structure factors P(hkl) with constant L
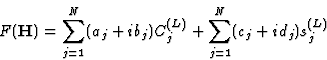 |
(2.5) |
where the unknown variables cos 2![]() and sin 2
and sin 2![]() have been denoted by C(L)j and S(L)j, respectively, and their known coefficients by aj, bj, cj and dj.
have been denoted by C(L)j and S(L)j, respectively, and their known coefficients by aj, bj, cj and dj.
aj = aj(h, k, fj, xj, yj) etc. where the exact form of dependence on h, k, fj, xj and yj may be obtained from Table 4 of International Tables for X-ray Crystallography, Vol. 1.
The 2N unknown variables C(L)j and S(L)j may be determined by a system of linear equations using ![]() )for
)for ![]() ).
).
If the phases of the ![]() are unknown the unobserved reflections may be used to obtain a system of homogeneous linear equations. Often it is of advantage to use in addition to the homogeneous equations one equation belonging to a strong structure factor whose phase may be fixed arbitrarily in centrosymmetrical space groups, and in the non-centrosymmetrical space groups in which the origin may have any position in the z-direction.
are unknown the unobserved reflections may be used to obtain a system of homogeneous linear equations. Often it is of advantage to use in addition to the homogeneous equations one equation belonging to a strong structure factor whose phase may be fixed arbitrarily in centrosymmetrical space groups, and in the non-centrosymmetrical space groups in which the origin may have any position in the z-direction.
Because the coefficients of these equations are inaccurate and, moreover, the structure factors are zero only approximately a more accurate solution for the values C(L)j and S(L)j may be obtained by using more equations than there are variables and by minimizing the sum of the squares of the deviations ![]() ,where
,where ![]() stands for the right side of equation (2.5) and F(H) is to be replaced by
stands for the right side of equation (2.5) and F(H) is to be replaced by ![]() in this relation. The C(L)j and S(L)j from the first calculation may be used to determine the phases of further structure factors. Taking these equations in addition to those used already, the number of equations increases and thus the accuracy of C(L)j and S(L)j is improved.
in this relation. The C(L)j and S(L)j from the first calculation may be used to determine the phases of further structure factors. Taking these equations in addition to those used already, the number of equations increases and thus the accuracy of C(L)j and S(L)j is improved.
If the F(hkl) with L = 1 are used, the atomic parameters zj of all atoms resolved in the (x, y)-projection follow from C(1)j= cos 2![]() and S(1)j = sin 2
and S(1)j = sin 2![]() and (C(1)j)2 + (Sj(1))2 = 1. The accuracy of the values zj may be further improved by using F(hkl) with L larger than one.
and (C(1)j)2 + (Sj(1))2 = 1. The accuracy of the values zj may be further improved by using F(hkl) with L larger than one.
2.2 The application of direct methods to centrosymmetric structures containing heavy atoms4
It is assumed that the positions of the heavy atoms are known and that there is a sufficient number of reflections whose signs are determined by the heavy atoms. These reflections do not obey the probability relation (2.6).
| (2.6) |
On subtracting the heavy atom contribution from the observed structure factors of these reflections, one obtains the sign of the light atom contributions for these reflections. Thereafter one can solve the remaining light atom structure by applying equation (2.6) to obtain the signs of the reflections that do not have contributions from the heavy atoms.
The procedure was used to solve the structure of the complex Au[S2C2(CN)2]2Au[S2CN(C4H9)2]2. The space group was found to be P21/c, with two formula units per unit cell. The reflections hkl (h = 2n, k + l = 2n) were all very strong and the gold atoms were placed at the (special) position 000, ![]() 00,
00, ![]()
![]()
![]() , and 0
, and 0![]()
![]() . 1337 observed 'strong' reflections (with equal positive contributions from the gold atoms) and 538 observed 'weak' reflections (without any contributions from the gold atoms) were used.
. 1337 observed 'strong' reflections (with equal positive contributions from the gold atoms) and 538 observed 'weak' reflections (without any contributions from the gold atoms) were used.
The first step was a calculation of the Wilson plot. The following expression was used:
| (2.7) |
where ![]() is the observed intensity on a relative scale, K = KL = KH is the scale factor,
is the observed intensity on a relative scale, K = KL = KH is the scale factor, ![]() denotes a summation over all light atoms in the unit cell, FH is the heavy atom contribution to the structure factor and BL and BH are the overall temperature factor parameters of the light and heavy atoms respectively. The average is taken over reflections h within a given sin
denotes a summation over all light atoms in the unit cell, FH is the heavy atom contribution to the structure factor and BL and BH are the overall temperature factor parameters of the light and heavy atoms respectively. The average is taken over reflections h within a given sin ![]() interval.
interval.
For the 'weak' reflections (FH = 0) the second term in equation (2.7) vanishes and a Wilson plot for these reflections gave the scale factor KL (1.29) and the value of BL (3.24 Å2). On substituting these results in equation (2.7) a Wilson plot for the 'strong' reflections gave the scale factor KH (1.26) and the value of BH (2.91 Å2). A small difference in KL and KH will not affect the following steps.
The second step is the calculation of the normalized structure factors E. The formulae normally used for the calculation of E values do not make sense for a structure containing heavy atoms. For the corresponding light atom structure the E values, EL, are defined by:
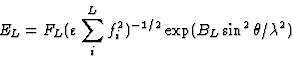 |
(2.8) |
where FL is the light atom contribution to the structure factor and, for space group ![]() = 2 for h01 and 0k0 reflections and
= 2 for h01 and 0k0 reflections and ![]() = 1 for all other reflections.6
= 1 for all other reflections.6
The 'strong' reflections have positive structure factors and we have ![]() ; the magnitude and the sign of the EL value is obtained by equation (2.8). This resulted in 365 signed EL values, with |EL| > 1.3. For the 'weak' reflections we have |FL| =
; the magnitude and the sign of the EL value is obtained by equation (2.8). This resulted in 365 signed EL values, with |EL| > 1.3. For the 'weak' reflections we have |FL| = ![]() and only the magnitude of the EL value is obtained. This resulted in 270 reflections with |EL| > 1.3.
and only the magnitude of the EL value is obtained. This resulted in 270 reflections with |EL| > 1.3.
The third step is the application of equation (2.6) to obtain the signs of the 'weak' reflections. When several interactions of the type (![]() ) = (h) + (
) = (h) + (![]() ) occur for |EL| > 1.3, where both Sh and
) occur for |EL| > 1.3, where both Sh and ![]() are known, several predictions of the sign
are known, several predictions of the sign ![]() are obtained by application of (2.6). These predictions should be reasonably consistent before
are obtained by application of (2.6). These predictions should be reasonably consistent before ![]() is considered to be determined and singly occurring interactions should never be trusted. We have followed a procedure similar to the sign correlation procedure. The origin is partly fixed by the choice of the gold atom positions and further determined by assigning arbitrary signs to two 'weak' reflections: 221 (|EL| = 4.0) and 34
is considered to be determined and singly occurring interactions should never be trusted. We have followed a procedure similar to the sign correlation procedure. The origin is partly fixed by the choice of the gold atom positions and further determined by assigning arbitrary signs to two 'weak' reflections: 221 (|EL| = 4.0) and 34![]() (|EL| = 2.9). We define the following sets of reflections, all |EL| > 2.0:
(|EL| = 2.9). We define the following sets of reflections, all |EL| > 2.0:
- h1 are 'strong' reflections, hkl(h = 2n, k + 1 = 2n).
- h2 are the two origin determining choices.
- h3 are the reflections h1 + h2 and
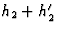 .
. - h4 are the reflections h1 + h3, h2 + h3 and
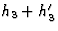 .
.
Continued application of equation (2.6) on 365 'strong' reflections, 2 reflections h2 and 24 reflections h4 resulted in the sign determination of 158 more 'weak' reflections with |EL| > 1.3. A Fourier synthesis revealed the positions of all of the light atoms, except the hydrogen atoms.
The above described procedure may be generalized for heavy atoms on general positions. In this case there also exist reflections with intermediate heavy atom contributions. For these reflections |FL| = |![]()
![]()
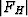 | and the lowest FL value is taken to avoid incorrect sign indications. In our opinion this procedure is well suited to an automatic solution of structures containing heavy atoms.
| and the lowest FL value is taken to avoid incorrect sign indications. In our opinion this procedure is well suited to an automatic solution of structures containing heavy atoms.
3. Steps of structure determination
1. Determine the space group and unit cell of the real structure.
2. Test for systematically strong intensities.
3. Determine the space group of the superposition structure (see examples).
4. Determine the superposition structure ![]() or at least the heavy atom positions(s) in
or at least the heavy atom positions(s) in ![]() .
.
5. Determine the complementary structure ![]() or the real structure.
or the real structure.
5.1 Compute and discuss the Patterson function of the complementary structure, if this corresponds to the systematically weak reflection.
5.2 Apply 'Direct methods' (see above).
5.3 Apply the method of 'linear structure factor equations'.
5.4 Resolve the ambiguity of the superposition structure using chemical knowledge, such as minimum distance between atoms, knowledge of groups, coordination polyhedra etc.
4. Examples
A. Demissidine hydroiodide8
Crystal data: C27H45NO.HI.![]() C2H5OH
C2H5OH
orthorhombic: P212121; a = 23.0 Å, b = 7.6 Å, c = 16.0 Å; Z = 4
Observed systematic intensity distribution:
![]()
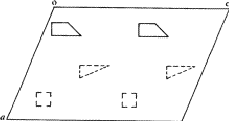
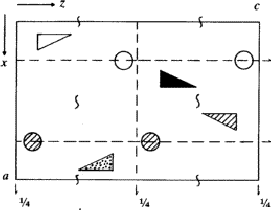
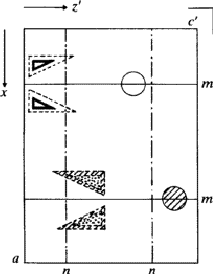
According to the chemical formula and number of molecules per unit cell there are 4 heavy atoms per unit cell, i.e. one per asymmetric unit. Thus the 2 heavy atoms related by a shift of c/2 (on account of systematic intensity distribution) must necessarily belong to the same set of equipoints. This results if and only if the atoms lie on screw dyads parallel to c (see Fig. 5), thus the set of equipoints in P212121
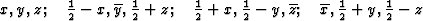
specializes to
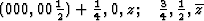
With ![]() this corresponds within the unit cell
this corresponds within the unit cell ![]() ,
, ![]() ,
, ![]() of the superposition structure, to the equipoints
of the superposition structure, to the equipoints
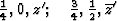
Obviously (Fig. 5), any of these two points lies on mirror planes perpendicular to ![]() and
and ![]() and are related by an n-glide plane perpendicular to
and are related by an n-glide plane perpendicular to ![]() . Thus the space group of the superposition structure is Pmmn.
. Thus the space group of the superposition structure is Pmmn.
 |
 |
The same result could have been obtained by scanning the orthorhombic higher symmetry group for such equipoints. Then the set of special positions (a) 00z,![]() would be found for Pmmn, which corresponds to the set found, after a shift of the origin by
would be found for Pmmn, which corresponds to the set found, after a shift of the origin by ![]() /4.
/4.
The space group for the superposition structure thus obtained may now be tested with the usual space group tests, and indeed, the hk0-reflections with h + k = 2n + 1 are weak (corresponding to the n-glide plane). The superposition structure thus contains for each of 4 symmetry related atoms (x, y, z) etc., of the real structure the following sets of 4 atoms.
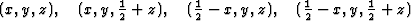
i.e. 4 atoms to any atom of the real structures. This superposition structure would be obtained, if the usual heavy atom technique could be applied, and would certainly be difficult to interpret.
The Patterson function gave, however, not only the z-coordinate of the heavy atom but also hinted that it may not lie exactly on the dyad screw, but only approximately so; this was confirmed by the Patterson of the complementary structure, obtained from the reflections with l = 2n + 1.
This indicated a deviation of xj from ![]() , and this deviation results in contribution of reflections with high values of h which even determine their phases.
, and this deviation results in contribution of reflections with high values of h which even determine their phases.
The iodine parameters were refined and with the resulting phases a first Fourier synthesis of the complementary structure was obtained in space group P212121.
This result was compared with the known part of the model and thus a part of the structure deduced and used as a starting point for the final determination of the real structure.
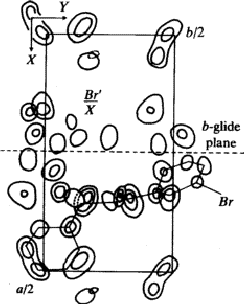
B. Piperidino-acet-m-bromo-anilide9
Crystal data: C13H17N2OBr
orthorhombic: Pbca; a = 23.65 Å, b = 12.66 Å, c = 9.37 Å; Z = 8
Observed systematic intensity distribution:
![]()
Space group of ![]() : Pbcm with lattice parameters
: Pbcm with lattice parameters
The 3-dimensional Patterson function explained the systematic distribution in the intensities by the particular position of the bromine-atom on the a-glide plane with the fractional coordinates x = 0.159, y = 0.193, z = 0.25. With the known position of the bromine atom (refined by least squares methods) the signs of most of the ![]() but not of the
but not of the ![]() were determined.
were determined.
With ![]() a 3-dimensional Fourier synthesis of the superposition structure was calculated. This
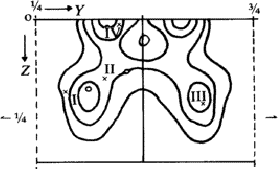
a 3-dimensional Fourier synthesis of the superposition structure was calculated. This ![]() involves perpendicular to c an additional mirror plane, not existing in the real structure, through the bromine atom. That is why each maximum in the synthesis has a corresponding reflected one (Fig. 6). But only one of these pairs corresponds to an atom in the real structure. In addition many maxima occurred in the Fourier synthesis which do not refer to atoms. Therefore the interpretation of the synthesis by the model of the molecule failed.
involves perpendicular to c an additional mirror plane, not existing in the real structure, through the bromine atom. That is why each maximum in the synthesis has a corresponding reflected one (Fig. 6). But only one of these pairs corresponds to an atom in the real structure. In addition many maxima occurred in the Fourier synthesis which do not refer to atoms. Therefore the interpretation of the synthesis by the model of the molecule failed.
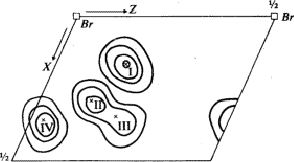
To preclude the spurious peaks in the Fourier synthesis a spatial minimum function M4(x, y, z)10 was derived from the Patterson function by using the known bromine-bromine vectors.
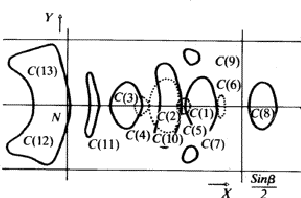
The comparison of Fourier synthesis and minimum function revealed to which of the pairs of peaks connected by the mirror plane atoms could be assigned. These peaks of the superposition structure are shown in Fig. 7. Its (x, y)-projection is identical with the projection of the real structure. A model of the molecule enabled us to determine the z-coordinates of the atoms by eliminating the ambiguity in the Fourier synthesis.
C. Acetamide hemihydrobromide11,12
Crystal data: (CH3CONH2)2.HBr
monoclinic: P21/c, a = 6.51 Å, b = 8.64 Å, c = 8.24 Å, ![]() = 113.1
= 113.1![]() ; Z = 2
; Z = 2
![]()
From Z = 2 and P21/c it follows that the bromine atom lies at the centre of symmetry forming, taken by themselves, an A-centred lattice. The ![]() correspond to a superposition structure with the space group A 2/m, which has a mirror plane perpendicular b in addition to the space group of the real structure.
correspond to a superposition structure with the space group A 2/m, which has a mirror plane perpendicular b in addition to the space group of the real structure.
The (x, z)-projection of the superposition structure (Fig. 8) is identical to the corresponding projection of the real structure. This projection, calculated with
![]()
and
![]()
where K is the scaling factor. The expressions ![]() and
and ![]() may be calculated because xj and zj are known, whereas K cos 2
may be calculated because xj and zj are known, whereas K cos 2![]() =
= ![]() and K sin 2
and K sin 2![]() =
= ![]() are the unknown values. From the known position of the heavy atom (bromine) most of the signs of the F(h1l)l=2n+1 could be determined and a system of equations (4.1) with a twelvefold overdetermination could be set up
are the unknown values. From the known position of the heavy atom (bromine) most of the signs of the F(h1l)l=2n+1 could be determined and a system of equations (4.1) with a twelvefold overdetermination could be set up
| (4.1) |
This system of equations was solved by least squares technique. Because the F(h1l) are on a relative scale the solutions ![]() were multiplied with a constant (1/K) so that (1/K)
were multiplied with a constant (1/K) so that (1/K)![]() = 1 is valid.
= 1 is valid.
Two values yj = yjo and yj = 1 - yjo are in keeping with the solutions Cj = (1/K)![]() (yjo) obtained. To find out which of these two values is correct, equations of the type (4.2):
(yjo) obtained. To find out which of these two values is correct, equations of the type (4.2):
| (4.2) |
were used. The bromine atoms do not contribute to the F(h1l)j=2n. The signs of these structure factors were unknown. Therefore the unobserved reflections F(h1l)l=2n and one strong reflection F(h1l)l=2n were used for setting up a system of inhomogeneous equations. The Sj = (1/k)![]() were less accurate than the Cj because this system of equations had only a twofold overdetermination. That is why the absolute values of the y-coordinates were calculated from the Cj, but the ambiguity was eliminated by the Sj. The results are shown in Fig. 9. Structure refinement proved these approximate values to be correct.
were less accurate than the Cj because this system of equations had only a twofold overdetermination. That is why the absolute values of the y-coordinates were calculated from the Cj, but the ambiguity was eliminated by the Sj. The results are shown in Fig. 9. Structure refinement proved these approximate values to be correct.
 |
D. 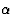 -Calcium tetraborate hydrate13
-Calcium tetraborate hydrate13
Crystal data: CaB2O4.4H2O
monoclinic: Pc or P2/c, a = 5.86 Å, b = 6.93 Å, c = 7.78 Å, ![]() = 94
= 94![]() ; Z = 2
; Z = 2
Observed systematic intensity distribution:
![]()
The intensity statistic of Howells, Phillips and Rogers14 using the I(hkl) showed that the real structure has the centrosymmetric space group P2/c.
The Patterson function showed in agreement with Z = 2 and P2/c that the calcium atom occupies a special position on the twofold rotation axis with parameters ![]() = 0,
= 0, ![]() =
= ![]() and
and ![]() approximately zero. This position is near the c-glide plane and thus explains why the reflections I(hkl)l=2n+1 are systematically weak.
approximately zero. This position is near the c-glide plane and thus explains why the reflections I(hkl)l=2n+1 are systematically weak.
On the other hand the calcium atom determined most of the signs of the F(hk0). The Fourier projection ![]() gave the positions of the oxygen and boron atoms. Because the signs of the F(hkl) with l = 2n + 1 were not determined by the contribution of the calcium atom the z-parameters of the atoms could not be derived from a Fourier synthesis based on the contributions of the calcium atom to the sign of the F(hkl). But with the SFE-method the approximate z-coordinates were easily obtained.
gave the positions of the oxygen and boron atoms. Because the signs of the F(hkl) with l = 2n + 1 were not determined by the contribution of the calcium atom the z-parameters of the atoms could not be derived from a Fourier synthesis based on the contributions of the calcium atom to the sign of the F(hkl). But with the SFE-method the approximate z-coordinates were easily obtained.
From the structure factor formula follows
Two systems of equations were set up. For the first system F(hk1) and for the second F(hk2) were used. In each case the unobserved structure factors and one strong structure factor with arbitrary sign was used. These systems of equations gave approximate values for C(L)j and S(L)j, by which Fc(hkl) were calculated.
By comparing the Fc(hkl) with the Fo(hkl) the signs of more structure factors could be determined. The corresponding equations were added to the previous systems of equations. In this way the overdetermination of the systems of equations was increased and the accuracy of the results improved. The final results obtained after several cycles are listed in the Table. The last column contains the refined parameter for comparison.
| Atom | C(1)j | S(1)j | C(2)j | S(2)j | zj | zj refined |
| Ca | - | 1.00 | -1.000 | - | 0.250 | 0.25 |
| O1 | - | 0.20 | 0.872 | - | 0.036 | 0.0359 |
| O2 | 1.00 | 0.51 | 0.703 | 0.756 | 0.070 | 0.0588 |
| O3 | 0.68 | 0.44 | 0.111 | 0.923 | 0.106 | 0.1042 |
| O4 | -0.66 | -0.74 | -0.338 | 0.680 | 0.842 | 0.8193 |
E. Dimethylaminomethylpinene12,15
Crystal data: C13H24NBr
monoclinic: P21, a = 11.37 Å, b = 8.62 Å, c = 7.48 Å, ![]() = 97.4; Z = 2
= 97.4; Z = 2
The x- and z-parameters of the bromine atom were determined from the Patterson synthesis and refined by Fourier methods. The y coordinate was chosen arbitrarily as ![]() . The 3-dimensional Fourier synthesis based on the phases of the
. The 3-dimensional Fourier synthesis based on the phases of the ![]() derived from the bromine contributions is a superposition structure with the space group P21/m with an additional mirror plane at
derived from the bromine contributions is a superposition structure with the space group P21/m with an additional mirror plane at ![]() . For the calculation of this synthesis only Fo(hkl) for 0k4 were available because the crystals were very small. The Fourier synthesis revealed the positions of all non-hydrogen atoms, most of them resolved in the x and z directions. Nearly all these atoms, however, located so closely to the pseudo mirror plane that the peak corresponding to one atom and its mirror image were not separated but formed an elliptical maximum with its peak on the mirror plane (Fig. 10).
. For the calculation of this synthesis only Fo(hkl) for 0k4 were available because the crystals were very small. The Fourier synthesis revealed the positions of all non-hydrogen atoms, most of them resolved in the x and z directions. Nearly all these atoms, however, located so closely to the pseudo mirror plane that the peak corresponding to one atom and its mirror image were not separated but formed an elliptical maximum with its peak on the mirror plane (Fig. 10).
 |
The main problem of the structure determination was to determine the small deviations of the light atoms from this pseudo mirror plane.
Analysis of the peak shape resulted in rather inaccurate values of the deviations from the mirror plane. Better values were obtained by the SFE method. To start with, the positions of all atoms in (x, z)-projection were refined by difference Fourier synthesis to an R value of 0.16. Using the formulae
![]()
and
![]()
where K1 and K2 are the scaling factors, two systems of equations were obtained taking Ao(hkl) equal to Fo(hkl). This may be done without creating large errors since the Bo(hkl), to which the bromine atoms do not contribute, are expected to be small. In these systems of equations only those Ao(hkl) were used whose signs could be deduced from the contributions ![]() of the bromine atoms.
of the bromine atoms.
With the abbreviations
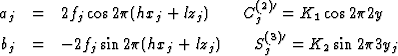
the systems of the equations have the form
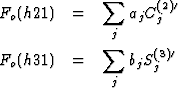
The structure factors Fo(h21) and Fo(h31) are on a relative scale. The scaling factors K1 and K2 were given such values that (1/K1)![]() = (1/K2)
= (1/K2)![]() = 1. Four values for the coordinate yj of any atom are in keeping with
= 1. Four values for the coordinate yj of any atom are in keeping with
![]()
Two of these values for any atom could be excluded by comparison with the Fourier synthesis of the superposition structure (see above). From the two remaining values one could be precluded for most of the atoms by using a model of the molecule (Fig. 10). The accuracy of the y coordinates obtained from the C(2)j was improved using the results obtained from S(3)j. The coordinates thus obtained were sufficiently accurate for a starting set for a least squares refinement of the real structure.
References
1. K. Dornberger-Schiff, Kritallografija, 6 (1961), 859.
2. L. Kutschabsky, Mber. Dt. Akad. Wiss., 7 (1965), 95, 509.
3. L. Kutschabsky and E. Höhne, Acta Cryst., 19 (1965), 747.
4. P. T. Beurskens and J. H. Noordik, Acta Cryst., A27 (1971) 187.
5. S. Parthasarathy, (1966). Z. Kristallogr. 123, 27.
6. H. Hauptman and J. Karle. Solution of the Phase Problem. I. The Centrosymmetric Crystal, A.C.A. Monograph No. 3 (1953).
7. P. T. Beurskens, (1963). Technical Report of Sign Correlation by the Sayre Equation. The Crystallography Laboratory, Univ. of Pittsburgh, Pennsylvania.
8. E. Höhne, Journ. prakt. Chem., 314 (1972), 371.
9. L. Kutschabsky, P. Leibnitz and J. P. Wenzel, Kristall und Technik, 9 (1974) 605.
10. M. J. Buerger, Vector Space and its application to Crystal Structure Analysis, Wiley, 1959.
11. G. Reck, Mber. Dt. Akad. Wiss. 9, (1967) 505.
12. L. Kutschabsky, S. Kulpe and G. Reck Acta Cryst., A27 (1971), 29.
13. D. Zeigan and L. Kutschabsky Mber. Dt. Akad. Wiss. 7 (1965), 876.
14. E. R. Howells, D. C. Phillips and D. Rogers, Acta Cryst., 3 (1950), 210.
15. L. Kutschabsky and G. Reck, Journ. prakt. Chem. 312 (1970), 896.


 and
and  ,
, - remaining atoms with half weight.
- remaining atoms with half weight.
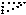 .
. 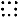 --atoms with negative half weight.
--atoms with negative half weight.
 in
in 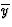 ,
, 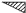 in 1/2 - y,
in 1/2 - y, 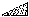 in 1/2 + y; the heavy atoms marked by circles. (b) superposition structure - Pmmn, derived from P212121; the reduced weights of all building units in general position (triangles) to a quarter compared with the weight of the heavy atoms (circles) is symbolized by dashed lines.
in 1/2 + y; the heavy atoms marked by circles. (b) superposition structure - Pmmn, derived from P212121; the reduced weights of all building units in general position (triangles) to a quarter compared with the weight of the heavy atoms (circles) is symbolized by dashed lines.