Anomalous dispersion of X-rays in crystallography

The contribution of resonance or dispersion effects to the atomic scattering factors

S. Caticha-Ellis

Introduction

The quantity usually measured in relation to each X-ray reflection is the intensity, which is proportional to |F(hkl)²| and hence it is |F(hkl)| that is determined experimentally. This quantity may be called the 'geometrical structure factor' since it depends only on the positions of atoms and not on any differences in their scattering behaviour. If the nature of the scattering, including any phase change, is identical for all atoms, then |F(hkl)| = $\vert F(\=h\=k\=l)\vert$ ; this result is sometimes known as Friedel's law.¹

As long ago as 1930, Coster, Knol and Prins² performed a most elegant experiment with zinc blende, using X-ray wavelengths selected to lie close to an absorption edge for zinc, but not for sulphur. They were able to demonstrate a failure of Friedel's law and to show that circumstances arise in practice in which the phase change produced by each atom in a unit cell is not the same. The different resonance that leads to this effect has become known as anomalous dispersion.

As radiation counters have been steadily improved, measurements of X-ray intensities have attained such a degree of accuracy that it is no longer acceptable to neglect the resonant effects which are bigger than the experimental errors by several orders of magnitude. As a matter of fact the effect can be detected also with film techniques in non-centrosymmetrical crystals by measuring the integrated intensities of symmetry-equivalent reflexions when the incident wavelength is adequately selected. Friedel's law does not hold in these cases, a phenomenon which was first used by Bijvoet and collaborators^3-13 to find the absolute configuration of some crystals. The finding of methods to solve crystal structures directly by using this phenomenon by Pepinsky and collaborators,^14-19 Ramachandran and Raman,^20-23 Caticha-Ellis^24-27 prompted a keen interest in this field.

Let us state from the outset that the usual name of 'anomalous dispersion' given to the effects studied in this article is entirely inadequate and misleading as it will soon be evident. However, I have kept it for convenience, since it has been used for years in the scientific literature, to avoid unnecessary confusions. It would certainly be more exact to rename the subject as 'resonance effects in the scattering of radiation', or directly 'resonance scattering of radiation' adding the qualifications nuclear or electronic according to the case. In the case of X-radiation there is always some resonant effect due to the continuous distribution of oscillator levels as we shall see below, so that the so-called normal scattering or non-resonant scattering is not normally found. The paradox then, is that 'anomalous scattering' is absolutely normal while 'normal scattering' occurs only as an ideal, oversimplified model, which can be used as a first approximation when studying scattering problems.

Calculations of the dispersion contribution to the atomic scattering factors made by several authors,^29-35 based on a method due to Parratt and Hempstead,³⁶ were used by many researchers to find the absolute structure of several crystals, as well as to completely solve many other crystal structures of increasing complexity including the solution of proteins.

Experimental determinations of a few dispersion corrections were performed by some authors in order to confirm the theoretical values and to investigate their dependence on the scattering angle and on the presence of more than one anomalous scatterer in the unit cell.^37-41

In an early paper, S. W. Peterson⁴² was able to measure differences in the intensities of symmetry equivalent reflexions in tyrosine hydrochloride and tyrosine hydrobromide. From measurements made on other crystals he established experimentally that this phenomenon was related to the presence of a heavy atom and of a polar axis. Peterson realized clearly the significance of these findings for direct structure determination by means of Fourier synthesis in non-centrosymmetrical crystals and in the same paper claims to have solved the crystal structure of both tyrosine hydrochloride and hydrobromide using only the information contained in the measurements themselves. It is interesting to note that the paper by Okaya, Saito and Pepinsky¹⁵ is dated only 23 days before that of Peterson.⁴²

In this article only the field of X-ray resonant scattering is reviewed. We shall mention here only in passing two other related resonant effects:

(a) Neutron resonant scattering
(b) Resonant scattering of gamma rays (Mossbauer effect).
(a) Resonant scattering of thermal neutrons produces in some elements

appreciable in-quadrature components of the scattering factors for neutron wavelengths of about 1 Å. Peterson and Smith⁴³ have shown the possibility of the crystallographic use of the phenomenon for substances containing such light elements as Li⁶ and B¹⁰ that can hardly produce any sizeable resonant effect with X-rays. Also some heavy elements such as Cd¹¹³, Sm¹⁴⁹, Eu¹⁵¹ and Gd¹⁵⁷ have appreciable in-quadrature components in the 1 Å region. Peterson and Smith have also observed that the number of elements with high in-quadrature components would be greatly enlarged by using neutrons of about 0.1 Å. The practical difficulty being of course the fact that the neutron flux in this region is very low. A hot source built in the reactor might be used to produce the required shift to higher thermal energies in the Maxwellian distribution.

The method has been analyzed by Ramaseshan,⁴⁴ applied by McDonald and Sikka⁴⁵ to solve the crystal structure of cadmium nitrate tetradeuterate and further extended by Sikka^46-48 and others.

(b) Certain nuclei, notably Fe⁵⁷ and Sn¹¹⁹ and also some rare earths have nuclear resonance levels that can absorb and emit gamma radiations with wavelengths in the useful range for crystallographic uses. The use of the emitted lines would have some definite advantages due to the fact that their widths are much smaller than those of the X-ray emission lines by a factor of the order of 10⁹. The main disadvantage is the very low intensity of the Mossbauer radiation in comparison with X-rays, a complicating factor from the point of view of the detectability and the statistics of the measurements. However, in some experiments where the sharpness of the line is essential, great advantage could be obtained from the use of such radiation.

In the list of references some papers on this subject have been included.^49-60

It is curious that in spite of the widespread use of anomalous scattering, no book had been written on this subject until 1974. The proceedings of an Inter-Congress Conference organized by the Commission on Crystallographic Apparatus of the International Union of Crystallography held in Madrid in that year thus became an all important reference which covers most of the crystallographic aspects of anomalous scattering.⁷⁵

In this chapter we review briefly the necessary theory to understand the origin of the dispersion effects and the basis for their calculations. The treatment is based on the four chapter of James' book: The Optical Principles of the Diffraction of X-Rays,⁶¹ which contains a detailed account of the subject.

In the classical approach to calculate the (normal) atomic scattering factors the hypothesis is made that the frequency of the incident wave $\omega_i$ is large in comparison with the resonance frequencies of the atom ( $\omega_K, \omega_L$ , etc., where the subindex refers to the electron shell), that is, those associated to the absorption edges. In practice, for the wavelengths normally used in crystallographic studies, this hypothesis can be approximately fulfilled only in the case of light atoms, but it is not generally true in most real cases. This is readily seen by comparing the values of the atomic absorption edges with those of the characteristic wavelengths of anticathodes normally used.

**Table 1**

Element	K absorption edge (Å)	K $\alpha$	K $\beta$
Element	K absorption edge (Å)	wavelengths (Å)

3-Li	226.6	240.0	-
4-C	43.6	44.0	-
11-Na	11.48	11.91	11.62
19-K	3.436	3.744	3.454
23-V	2.269	2.505	2.284
24-Cr	2.070	2.291	2.085
26-Fe	1.743	1.937	1.756
27-Co	1.608	1.790	1.607
28-Ni	1.488	1.659	1.500
29-Cu	1.380	1.5418	1.392
42-Mo	0.6197	0.7106	0.6322
55-Cs	0.345	0.402	0.354
57-La	0.318	0.372	0.328

In Table 1 we quote some values of the K absorption edges and of the emitted K wavelengths for some elements. It is obvious from Table 1 that, for instance, if one has iron or cobalt atoms in a sample, Cu $K\alpha$ radiation will produce strong resonance effects since this wavelength is slightly smaller than the K-absorption edges of these elements and consequently heavily absorbed by them. This is also the case for V atoms with Cr $K\beta$ radiation or Cr atoms with Fe $K\alpha$ , etc. Obviously in these cases the calculation of the atomic scattering factor f₀ without resonance effects is no longer valid since $\omega_i$ is comparable to $\omega_K$ .

It is then necessary to study in what way the values of f₀ will be altered to f by resonance. Three main different approaches have been used to calculate the dispersion corrections:

(a) Hönl^62-64 used hydrogen-like eigenfunctions to obtain the oscillator strengths and from them the photoelectric absorption cross-sections. Hönl's method, restricted to the K-electrons contribution, was extended by other authors.
(b) Parratt and Hempstead's approach³⁶ used semi-empirical relations for the photoelectric absorption cross-section from which f' and f'' are obtained.
(c) Cromer and Liberman³⁵ used relativistic Slater-Dirac wave functions.

Recently these methods were reviewed by Wagenfeld.¹⁰⁶

There is a close parallelism between the classical and the quantum treatment; we give next a scheme of James' classical treatment.

Scattering by a classical dipole oscillator

In the classical theory of dispersion the atom is assumed to scatter radiation as if it was formed by dipole oscillators whose natural frequencies are those of the absorption edges of the electronic shells. These oscillators may be thought of as originated by simple harmonic vibrations of the electronic charges, as for instance, the movement of an electron of mass m around the positive nucleus assumed to be at rest. An electromagnetic wave falling on the atom and having an instantaneous electric field $\textbf {E} = \textbf {E}_0e^{i\omega t}$ at the position of the dipole, sets the electron in oscillation, the displacement of the atom satisfies then the differential equation:

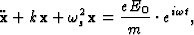$\begin{displaymath} \uml {\textbf x} + k{\textbf x} + \omega^2_s{\textbf x} = \frac{{eE}_{0}}{m}\cdot e^{i\omega t},\end{displaymath}$

(1)

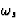where k is a damping factor and $\omega_s$ the natural circular frequency of the electron.

The forced solution of (1) is:

$\begin{displaymath} {\textbf x} = \frac{{eE}_{0}}{m}\cdot \frac{e^{i\omega t}}{\omega^2_s - \omega^2 + ik \omega},\end{displaymath}$

(2)

and the dipole moment:

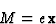$\begin{displaymath} M = e{\textbf x}\end{displaymath}$

(3)

which has its axis in the direction of the applied field E.

This oscillating dipole radiates with the same frequency of oscillation; the amplitude of the wave at a unit distance in the equatorial plane being

$\begin{displaymath} A = \frac{e^2}{mc^2}\cdot \frac{\omega^2E_0}{\omega^2_s - \omega^2 + ik\omega}\end{displaymath}$

(4)

The scattering factor of the dipole is defined, as usual, as the ratio of the scattered amplitude A to that scattered by a free electron A_e under the same conditions. In this case, A_e, the Thomson amplitude, is obtained by taking $\omega_s$ = 0, k = 0:

$\begin{displaymath} A_e = -\frac{e^2}{mc^2}\cdot E_0\end{displaymath}$

(5)

The dipole scattering factor is then given by

$\begin{displaymath} f = \frac{A}{A_e} = \frac{\omega^2}{\omega^2 - \omega^2_s - ik\omega}\end{displaymath}$

(6)

If the incident frequency $\omega$ tends to $\omega_s$ the scattering factor becomes imaginary.

Expression (6) is very important since the atomic scattering factor results from a superposition of similar terms by considering the atom as made up of a distribution of dipole oscillators. Let us denote by $f^{\prime}$ ( $\omega$ ) and $f^{\prime\prime}$ ( $\omega$ ) respectively the real and the imaginary parts of f:

$\begin{displaymath} f = f^{\prime} + if^{\prime\prime}\end{displaymath}$

(7)

$\begin{displaymath} f^{\prime}(\omega) = \frac{\omega^2(\omega^2 - \omega^2_s)}{(\omega^2 - \omega^2_s)^2 + k^2\omega^2}\end{displaymath}$

$\begin{displaymath} f^{\prime\prime}(\omega) = \frac{k\omega^3}{(\omega^2 - \omega^2_s)^2 + k^2\omega^2}\end{displaymath}$

Apart from the functional dependence of f on the frequency, the main conclusion is that the scattering factor contains a real and an imaginary component, i.e. an in-phase and a quadrature component.

If a medium is composed of N similar dipoles per unit volume, it can be shown that the refractive index n is also complex and given by

$\begin{displaymath} n = 1 - \frac{2{\pi}Ne^2}{m\omega^2}\cdot f\end{displaymath}$

(8)

which we rewrite as

$\begin{displaymath} n = 1 - \alpha - i\beta,\end{displaymath}$

with

$\begin{displaymath} \alpha = \frac{2{\pi}Ne^2}{m\omega^2}\cdot f^{\prime},\end{displaymath}$

(9)

$\begin{displaymath} \beta = \frac{2{\pi}Ne^2}{m\omega^2}\cdot f^{\prime\prime}.\end{displaymath}$

The fact that n is complex and particularly so when $\omega$ approximates $\omega_s$ , indicates that the medium is absorbent. In fact by taking the origin of phases at an arbitrary origin O, the phase, after the wave has travelled a distance r, is

$\begin{displaymath} e^{-i(2\pi/\lambda)nr} = e^{-i(2\pi/\lambda)r(1 - \alpha - i... ...{- (2\pi i\lambda)r(1 - \alpha)}\cdot e^{-(2\pi/\lambda)r\beta}\end{displaymath}$

where the second factor is a real exponential with negative argument indicating a decrease in the wave amplitude. The decrease in intensity is given by $e^{- (4\pi/\lambda)r\beta}$ or $e^{-{\mu}r}$ , $\mu$ being the linear absorption coefficient, then

$\begin{displaymath} \mu = \frac{4{\pi}\beta}{\lambda} = \frac{2\omega\beta}{c} = \frac{4{\pi}Ne^2}{mc\omega}\cdot f^{\prime\prime}(\omega)\end{displaymath}$

(10)

After substitution of $f^{\prime\prime}$ and division by N one obtains the linear absorption coefficient per dipole in the medium for the circular frequency:

$\begin{displaymath} \mu_a(\omega) = \frac{4{\pi}e^2}{mc}\cdot \frac{k\omega^2}{(\omega^2 - \omega^2_s)^2 + k^2 \omega^2}.\end{displaymath}$

(11)

Reciprocally, the imaginary component of the dipole scattering factor of an absorbent medium is given by:

$\begin{displaymath} f^{\prime\prime}(\omega) = \frac{mc}{4{\pi}e^2}\cdot {\omega}{\mu}_a(\omega).\end{displaymath}$

(12)

If $\mu_a$ ( $\omega$ ) was a measurable magnitude, the expression (12) would provide a way to calculate the imaginary component $f^{\prime\prime}$ by using the experimental values of the absorption coefficients. This conclusion, obtained for a dipole, is clearly true also for an atom, so that the tables of absorption coefficients can be regarded as giving the imaginary components of the atomic scattering factors except for a scaling coefficient.

Obviously $f^{\prime\prime}$ and $\mu_a$ have their respective maximum values for a frequency close to $\omega_s$ ; the value of the damping coefficient k being the breadth of the absorption peak at half height. The smaller the value of k the sharper the absorption peak which then becomes a line. If a beam of white radiation is passing through the medium only frequencies near to $\omega_s$ will be significantly absorbed.

The atomic scattering factor. The oscillator strength

Assuming the simple case where k is very small and $\omega$ is quite different from $\omega_s$ , then, we obtain approximately:

$\begin{displaymath} f^{\prime} = \frac{\omega^2}{\omega^2 - \omega^2_s}\end{displaymath}$

(13)

and

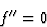$\begin{displaymath} f^{\prime\prime} = 0\end{displaymath}$	(14)
$\begin{displaymath} \mu_a = 0\end{displaymath}$

Under these conditions, we shall concentrate on the real part $f^{\prime}$ of the dipole scattering factor. Let us now consider an atom containing g(1), $\dots$ , g(2), $\dots$ , g(s), $\dots$ dipole oscillators of natural frequencies $\omega_1$ , $\dots$ , $\omega_2$ , $\dots$ , $\omega_s$ , $\dots$ respectively. Expression (13) can now be generalized by summing the contributions of all the oscillators contained in the atom so as to give the real part of the atomic scattering factor:

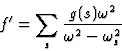$\begin{displaymath} f^{\prime} = \sum_s\frac{g(s)\omega^2}{\omega^2 - \omega^2_s}\end{displaymath}$

(15)

The number g(s) of dipole oscillators of natural frequency $\omega_s$ existing in an atom is called the 'oscillator strength' corresponding to that particular frequency. The calculation of the oscillator strength is the main difficulty in obtaining the resonance contributions to the atomic scattering factors.

We shall not discuss here either the implications or the validity of the generalization just made which has far reaching consequences. A comparison of these arguments with those from the quantum theory of atomic scattering is quite adequate, but will not be undertaken here, since we rather intend to concentrate on the applications of anomalous scattering. The reading is referred, for such a comparison, to James' book.⁶¹

If we now re-examine the foregoing arguments we note that the calculations were explicitly made for points located in the plane perpendicular to the electric vector of the incident wave, that is equivalent to taking the polarization factor equal to unity. That is why the expression (15) obtained for the atomic scattering factor is independent of the diffraction angle. In fact, as it is well known, this is not generally true, for instance for a spherically symmetric atom, f = f(sin $\theta$ / $\lambda$ ).

f could be independent of $\theta$ if the incident wavelength was big with respect to the dimensions of the atom where the electron density is not negligible; notwithstanding the opposite is the case normally encountered in practice since the atomic dimensions and the wavelengths normally used in crystallography are of the same order of magnitude, namely, one to two ångströms.

However, our aim is to obtain only the dispersion terms and not the entire atomic scattering factor. The terms which correspond, for instance, to the K absorption edge are important only when the incident frequency $\omega$ is close to $\omega_K$ . The relevant electron distribution in the case is only that of the K electrons. It is then easy to verify that $\lambda_K$ is much larger than the dimensions of the atomic region where the K-electron density is appreciable; this means that the phase difference in the scattered waves due to the difference in position of the K electrons within the atom will be small and their total contribution will thus be practically independent of the diffusion angle. The same arguments are valid, mutatis mutandis, to the case of L, M, etc., electrons. It follows that the resonant contribution to the atomic scattering should be nearly independent of the diffusion angle, which means that the hypothesis used in the previous calculations can be applied to a fair approximation.

In the quantum mechanical treatment the analogues of the classical oscillator strengths are magnitudes g(k, n) which are proportional to the transition probability of an electron passing from a state k to a state n. For an electron atom,

$\begin{displaymath} \sum_{n}g(k, n) = 1\end{displaymath}$

(16)

i.e. the Thomas-Reiche-Kuhn sum rule, holds. This rule, extended to the case of a many-electron atom, states that the sum of the oscillator strength is equal to the atomic number Z.

Summing up, the atom scatters as if it was composed by dipole oscillators of given natural frequencies, identical to the Bohr frequencies, their number or oscillator strength being proportional to the transition probability of state k into state n. It is here important to note that the states k include all the discrete states of negative energy and the continuum of positive energy states.

The oscillator density

For the continuum of positive energy states, the summations become integrals. The natural frequency for them changes continuously, so that rather than the discrete value g( $\omega_s$ ) it is necessary to define the oscillator density (dg/d $\omega$ ) at the frequency $\omega$ . The number of oscillators with frequencies between $\omega$ and $\omega$ + d $\omega$ is (dg/d $\omega$ )d $\omega$ . This number is zero for $\omega$ < $\omega_s$ , where $\omega_s$ is the frequency associated with the s absorption edge. The oscillator strength due to all K electrons for instance, is obtained by integration in the whole range of frequencies $\omega_K$ to $\infty$ , i.e. the interval where the number of oscillators related to the continuum of positive energy states is different from zero:

$\begin{displaymath} g_K = \int^{\infty}_{{\omega}_K} \Big(\frac{\mbox{d}g}{\mbox{d}\omega}\Big)_K \mbox{d}\omega.\end{displaymath}$

(17)

In words, g_K is given by the probability of transition of the K electrons to all permissible states. Wheeler and Bearden⁶² applied the sum rule and obtained

$\begin{displaymath} g_K = 2\Big(1 - \sum_m g(k, m)\Big)\end{displaymath}$

(18)

where g(k, m) is the oscillator strength of the virtual oscillator of the transition $k{\rightarrow}m$ , where m is an occupied state. The sum in (18) then needs be taken only on the relatively few occupied states. g_K is then less than 2. Analogous considerations apply to the other shells, so that for an s shell one would have:

$\begin{displaymath} g_s = n_s \Big(1 - \sum_m g(s, m)\Big)\end{displaymath}$

(19)

when n_s is the multiplicity of the shell. This method of calculation applied by Wheeler and Bearden in 1934 to the K-electrons of a few atoms has apparently some advantages which have not been exploited again.

Bethe⁶⁵ calculated the oscillator strengths g(s, m) for hydrogen-like atoms.

From equation (19), the generalized Thomas-Reiche-Kuhn rule can be obtained observing that: g(s, m) = -g(m, s). The justification of this argument is of a statistical nature, for both transitions should have the same probability, since their net result must average zero.

Thus,

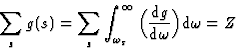$\begin{displaymath} \sum_s g(s) = \sum_s \int^{\infty}_{{\omega}_s} \Big(\frac{\mbox{d}g}{\mbox{d}\omega}\Big)\mbox{d}\omega = Z\end{displaymath}$

(20)

$\begin{displaymath} s = K, L, M, \dots\end{displaymath}$

Equation (15), which can be rewritten:

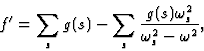$\begin{displaymath} f^{\prime} = \sum_s g(s) - \sum_s \frac{g(s){\omega}^2_s}{{\omega}^2_s - {\omega}^2},\end{displaymath}$

(15')

becomes

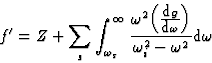$\begin{displaymath} f^{\prime} = Z + \sum_s \int^{\infty}_{{\omega}_s} \frac{{\o... ...}{\mbox{d}\omega}\Big)}{{\omega}^2_i-{\omega}^2} \mbox{d}\omega\end{displaymath}$

(21)

$\begin{displaymath} s = K, L, M, \dots\end{displaymath}$

Equation (21) only applies when $\omega_i$ , the incident frequency, corresponds to a wavelength ${\lambda}_i$ large in comparison with the atomic dimensions. For frequencies higher than the natural frequencies of the atom and wavelengths of the order of the atomic dimensions, we may substitute Z by f₀, the normal scattering factor, with good approximation and write:

$\begin{displaymath} f^{\prime} = f_0 + \Delta f^{\prime}\end{displaymath}$

where

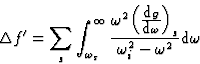$\begin{displaymath} {\Delta}f^{\prime} = \sum_s \int^{\infty}_{{\omega}_s} \frac... ...\mbox{d}\omega}\Big)}_s}{{\omega}^2_i-{\omega}^2}\mbox{d}\omega\end{displaymath}$

(22)

Equations (21) and (22) are valid for any wavelength except for very short ones when relativistic corrections are not negligible. Damping has also been neglected: an approximation usually adopted in the calculation of ${\Delta}f^{\prime}$ and ${\Delta}f^{\prime\prime}$ , which however does not introduce unduly large errors except in the intervals

$\begin{displaymath} x = \frac{{\omega}_i}{{\omega}_s} \cong 1 \pm 0.005,\end{displaymath}$

around the absorption edges.

The 'normal' scattering factor f₀ has Z as a limiting value at low frequencies for any angle of scattering and at very low angles for any frequency. To obtain the real part of the dispersion correction one has to integrate equation (22) so that the values of the oscillator densities (dg/d $\omega$ ) have to be calculated. This can be done from the atomic wave-functions. Hönl^62-63 made calculations for the K and L electrons which were assumed to be hydrogen-like. The result was quite satisfactory for the K electrons but not for the L's. Later Hönl's method was applied by Eisenlohr and Müller⁶⁶ to the L electrons of several atoms.

The Hartree wave functions were tried by Cromer⁶⁷ to obtain the oscillator strengths, but he found them inadequate for this purpose, particularly for the heavy elements. He tried then the relativistic wave functions without exchange, calculated by Cohen⁶⁸ in the test cases of tungsten and uranium, finding better results. New relativistic wave functions computed by Lieberman, Waber and Cromer⁶⁹ became available for all atoms, which included Slater's^{70- 71} approximate exchange correction and Latter's⁷² self-interaction term. Using these wave functions, Cromer⁶⁷ calculated a set of oscillator strengths which have been in use up to now. From them, he obtained a set of dispersion corrections for elements 10 through 98 for five different wavelengths.

Use of the photoelectric absorption measurements

There is, in principle, a simpler approach to the calculation of the dispersion terms by using the following relationship between the oscillator density functions (dg/d $\omega_s$ ) and the photoelectric absorption coefficient $\mu(\omega)$ :⁶¹

$\begin{displaymath} \Big(\frac{\mbox{d}g}{\mbox{d}\omega}\Big) = \frac{mc}{2{\pi}^2e^2} {\mu}(\omega),\end{displaymath}$

(23)

which indicates that the oscillator density (dg/d $\omega$ ) is simply proportional to $\mu(\omega)$ .

Using experimental values of $\mu$ ( $\omega$ ) one could obtain values for the oscillator densities from equation (23). However, accurate values for $\mu$ ( $\omega$ ) are not presently available for all the elements in a useful range of $\omega$ . Then, the usefulness of an empirical method to obtain (dg/d $\omega$ )_s, g_s, ${\Delta}f^{\prime}$ and ${\Delta}f^{\prime\prime}$ based on the experimental values of $\mu$ ( $\omega$ ) is very limited.

A semi-empirical method has been used by taking the well known approximate functional dependence of $\mu$ ( $\omega$ ):

$\begin{displaymath} \mu(\omega) = \left\{ \begin{array} {ll} ({\omega}_s/{\omeg... ...} \gt {\omega}_s \\ 0 & \omega < {\omega}_s\end{array} \right.\end{displaymath}$

(24)

where n has a value of about 3 which, however, changes with the atomic number and with the absorption edge involved. Moreover $\mu$ ( $\omega$ ) is not strictly zero below $\omega_s$ .

By choosing the best experimental values for n and $\mu$ ( $\omega_s$ )integration of equation (17) should provide reasonably good values of g_s. One can substitute, in the general case, equations (23) and (24) in (17) to obtain:

$\begin{displaymath} g_s = \frac{mc}{2{\pi}^2e^2}\frac{{\omega}_s}{n - 1} {\mu}({\omega}_s).\end{displaymath}$

(25)

Analogously, we obtain from (22) the contribution ${\Delta}f^{\prime}_s$ of electrons s to ${\Delta}f^{\prime}$ :

$\begin{displaymath} {\Delta}f^{\prime}_s = \frac{mc}{2{\pi}^2e^2} {\mu}({\omega}... ...\omega}^2 \mbox{d}\omega}{({\omega}^2_i-{\omega}^2) {\omega}^n}\end{displaymath}$

(26)

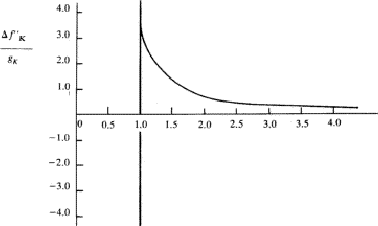
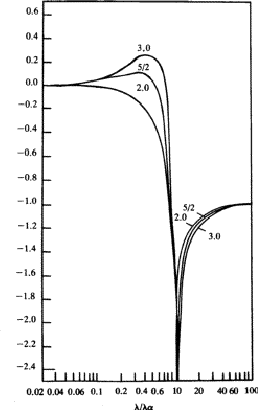
Equation (26) has been integrated in the general case by Parratt and Hempstead.³⁶ These authors have expressed their results in the form of 'universal anomalous dispersion curves', which are essentially the representation of the integral in equation (26) with n as a parameter, as a function of ${\lambda}_i/{\lambda}_s$ . When damping is neglected, these curves are independent of the atomic number and of the electronic shell involved. To obtain a particular value of ${\Delta}f^{\prime}_s$ , the value on the curve with the correct value of n is multiplied by the oscillator strength calculated from equation (25). ${\Delta}f^{\prime}$ is then obtained by summation through all s = K, L, M, $\dots$ shells. The shape of the curves, reproduced in Fig. 1, is quite instructive. They are qualitatively correct and show that the dispersion contributions from the various electron shells are rarely negligible, or, in other words, as Parratt and Hempstead point out, there is practically no region of normal dispersion.

**Figure 1:** Universal anomalous dispersion curves according to Parratt and Hempstead. The value of Re(J_q - 1) times the oscillator strength gives the anomalous dispersion correction for any atomic shell of electrons.
$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

Since the method used by Parratt and Hempstead is based on experimentally determined values and uses exact integrations one should expect results in better agreement with the independent measurements made of the atomic scattering factor than is the case for the values obtained using Hönl's theory based on hydrogen-like electron shells. The calculations made by Parratt and Hempstead for the K region of copper and the L region of tungsten using only one term in the oscillator distribution for each electron shell, actually showed a less satisfactory agreement than Hönl's theory. This rather discouraging result was attributed by Parratt and Hempstead to (a) the difficulties inherent in the experimental measurements and (b) neglect of parts of the calculations in previous comparisons.

In fact, the experimental differences (f - f₀) which they used to compare their calculations were presumably of a rather low precision, since they were based on values of f measured in the early 30's and presumably not very precise. The value of f₀ subtracted in the iron case was the Thomas-Fermi f₀ = 17.3 for plane (110) of Fe.

It would be interesting to remeasure the values of f using modern techniques and subtract better values of f₀ as are currently available nowadays in order to make a definite comparison.

The imaginary component 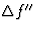${\Delta}f^{\prime\prime}$

The imaginary component of the atomic scattering factor corresponds to a component of the scattered radiation from the atom having a phase in the forward direction that lags ${\pi}$ /2 behind that of the primary wave.

As is known, in the (Thomson) scattering by free electrons, or very approximately in the case of bound electrons and very high frequencies the phase-lag of the forward scattered wave is ${\pi}$ . As the frequency of the incident radiation approaches an absorption edge the amplitude of the imaginary component increases so that the resultant phase may differ significantly from ${\pi}$ .

In order to have an appreciable resonant effect, the incident frequency must lie very close to one of the natural oscillator frequencies. However, since the virtual oscillators in an atom have frequencies covering a continuous distribution, the resonance effect may be appreciable even for frequencies not so close to one of the absorption edges, for it still coincides with one of the continuous distribution. A system having a discrete set of oscillators would then behave in an entirely different way.

Let us consider, for instance, the case of K electrons. As we know ${\Delta}f^{\prime\prime}_K$ = 0 for $\omega_i$ < $\omega_K$ . It is then only necessary to consider frequencies larger than $\omega_K$ , since only in this case they may coincide with those of the continuum.

An extension of equation (12) gives the relationship between the K-contribution to the absorption coefficient and ${\Delta}f^{\prime\prime}_K$ ,the K-contribution to the imaginary component of the atomic scattering factor:

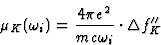$\begin{displaymath} {\mu}_K({\omega}_i) = \frac{4{\pi}e^2}{mc{\omega}_i}\cdot{\Delta}f^{\prime\prime}_K\end{displaymath}$

(12')

From relation (23) between the oscillator density and the absorption coefficient one obtains:

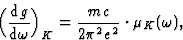$\begin{displaymath} \Big(\frac{\mbox{d}g}{\mbox{d}\omega}\Big)_K = \frac{mc}{2{\pi}^2e^2}\cdot{\mu}_K(\omega),\end{displaymath}$

(23')

and then:

$\begin{displaymath} {\Delta}f^{\prime\prime}_K = \frac{\pi}{2} {\omega}_i \Big(\frac{\mbox{d}g}{\mbox{d}\omega}\Big)_K.\end{displaymath}$

(27)

Assuming a dependence of ${\mu}_K$ on $\omega$ according to (24),

$\begin{displaymath} {\Delta}f^{\prime\prime}_K = \frac{mc}{4{\pi}e^2} {\omega}_i \Big(\frac{{\omega}_K}{{\omega}_i}\Big)^n \cdot{\mu}({\omega}_K),\end{displaymath}$

(28)

is obtained, giving the K-contribution as a function of the incident frequency.

It is interesting to express the relationship between ${\Delta}f^{\prime\prime}_K$ and the corresponding oscillator g_K:

$\begin{displaymath} {\Delta}f^{\prime\prime}_K = \frac{\pi}{2}(n - 1) \Big(\frac{{\omega}_K}{{\omega}_i}\Big)^{n-1}\cdot g_K\end{displaymath}$

(29)

valid for $\omega_i$ < $\omega_K$ , which was obtained from equations (25) and (28).

Figure 2 represents ${{\Delta}f^{\prime\prime}_K}/{g_K}$ as a function of $x = {\omega}_i$ / $\omega_K$ , the effect of damping is indicated qualitatively by the dotted line.

The atomic scattering factor may be expressed as the sum of three terms:

$\begin{displaymath} f = f_0 + {\Delta}f^{\prime} + i{\Delta}f^{\prime\prime}\end{displaymath}$

where f₀ is a function of (sin $\theta$ )/ $\lambda$ , whose values calculated for atoms with spherical symmetry are tabulated, for instance, in the International Tables for X-Ray Crystallography, Vol. 3.⁷³ As was shown in this chapter the components, ${\Delta}f^{\prime}$ and ${\Delta}f^{\prime\prime}$ are not negligible when the incident frequency is slightly larger than that of the absorption edges of the atom. These two components, related to the photoelectric absorption coefficients as well as to the oscillator density and oscillator strengths associated to the atom, are given by:

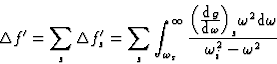$\begin{displaymath} {\Delta}f^{\prime} = \sum_s {\Delta}f^{\prime}_s = \sum_s \i... ...omega}\Big)_s{\omega}^2\mbox{d}\omega}{{\omega}^2_i-{\omega}^2}\end{displaymath}$

(30)

and

$\begin{displaymath} {\Delta}f^{\prime\prime} = \sum_s {\Delta}f^{\prime\prime}_s... ..._s = \sum_s \frac{mc}{4{\pi}e^2} {\omega}_i{\mu}_s({\omega}_i).\end{displaymath}$

(31)

$\begin{displaymath} s = K, L, M, N, \dots\end{displaymath}$

It is possible by using quantum mechanical methods to determine the oscillator densities from the atomic wave functions. This method was first introduced by Hönl,^62-63 who, of course, did not have at the time the computing facilities nowadays provided by modern computers, so that his main contribution was in developing the method and calculating some values for hydrogen-like K-electrons.

**Figure 2:** Imaginary dispersion correction as a function of incident frequency according to James.
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

A method based on the utilization of the relationships between oscillator strengths and densities from one side and photoelectric absorption coefficients on the other, developed by Parratt and Hempstead,³⁶ did not succeed initially in providing satisfactory results due mainly to the lack of good experimental values of the absorption coefficients and also, to my belief, to the lack of reliable experimental and theoretical atomic scattering factors.

Cromer⁶⁷ used self-consistent field relativistic Dirac-Slater wave functions to calculate accurate oscillator strengths for elements 10 through 98. He calculated then the dispersion terms ${\Delta}f^{\prime}$ by using Parratt and Hempstead's³⁶ solution of equation (26) and summing over the different absorption edges. The imaginary terms $f^{\prime\prime}$ were also computed for the same elements from equation (29). The values of the parameters n used by Cromer,⁶⁷ Dauben and Templeton²⁸ and other authors were taken from the discussion by Parratt and Hempstead,³⁶ as n = 11/4 for the 1s1/2 edge, n = 7/3 for the 2s1/2 edge and n = 5/2 for all other edges.

The use of the dispersion terms for the solution of crystal structures, which will be discussed later, made it necessary to obtain the values of ${\Delta}f^{\prime}$ for a wide range of wavelengths for atoms where the anomalous dispersion effects are significant. This calculation was performed by Saravia and Caticha-Ellis³³ for elements 20 through 83 for 32 different $K\alpha$ wavelengths ranging from Ti $K\alpha$ (2.75 Å) to I $K\alpha$ (0.435 Å), by using the method of Parratt and Hempstead,³⁶ the absorption edges from Cauchois and Hulubei⁷⁴ and the oscillator strengths from Cromer.⁶⁷ Essentially the same calculations were later performed by Hazell³⁴ for eleven $K\beta$ radiations.

References

1. G. Friedel, Comptes Rendus 157 (1913), 1533.

2. D. Coster, K. S. Knol and J. A. Prins, Z. f. Phys. 63 (1930), 345.

3. J. M. Bijvoet, Proc. Kon. Ned. Akad. Wet, 52 (1949) 313.

4. A. F. Peerdeman, A. J. von Bommel and J. M. Bijvoet, Nature, Lond. 165, (1951), 271.

5. A. F. Peerdeman, A. J. von Bommel and J. M. Bijvoet, Proc. Kon. Ned. Akad. Wet. 54, (1951), 16.

6. A. J. von Bommel, Proc. Roy. Soc. Amsterdam, (1953). 268.

7. J. M. Bijvoet, (1954). Nature 173, 888.

8. J. Trommel and J. M. Bijvoet, (1954). Acta Cryst. 7, 703.

9. J. M. Bijvoet, (1955). Endeavour, 14, 71.

10. A. F. Peerdeman and J. M. Bijvoet (1956). Acta Cryst. 9, 1012.

11. A. F. Peerdeman, (1956). Acta Cryst. 9, 824.

12. A. De Vries, (1958). Nature 181, 1193.

13. J. M. Bijvoet, Abstract 19.7. 5th. Congr. IUCr. Cambridge, England (1960).

14. Y. Okaya, Y. Saito and R. Pepinsky (1955), Phys. Rev. 98, 1857.

15. R. Pepinsky and Y. Okaya, (1956), Proc. Natl. Acad. Sci. U.S. 42, 286.

16. Y. Okaya and R. Pepinsky (1956), Phys. Rev. 103, 1645.

17. R. Pepinsky (1956). Record Chem. Progress (Kresge Hooker, Sci. Lib.) 17, 145.

18. R. Pepinsky and Y. Okaya (1957), Phys. Rev. 108, 1231.

19. Y. Okaya and R. Pepinsky, In Computing Methods and the Phase Problem in X-Ray Crystal Analysis, p. 273-299, Pepinsky and Speakman (eds.), Pergamon Press, London (1961).

20. G. N. Ramachandran and S. Raman, (1956). Current Sci. (India), 25, 348.

21. S. Raman, (1958). Proc. Ind. Acad. Sci. A, 47, 1.

22. G. N. Ramachandran and S. Raman, (1959). Acta Cryst. 12, 957.

23. S. Raman, (1959). Acta Cryst. 12, 964.

24. S. Caticha Ellis, (1959) Curso Latinoamericano de Cristalografia-Univ. de Chile. UNESCO--Lecture notes. (Oct. 1959).

25. S. Caticha Ellis. (1961a). Bol. Facultad Ingenieria y Agrimensura. Montevideo VII, n $^{{\rm o}}$ 13, 447.

26. S. Caticha Ellis, (1961b). Bol. Facultad Ingenieria y Agrimensura. Montevideo VII, n $^{{\rm o}}$ 13, 461.

27. S. Caticha Ellis, (1962). Acta Cryst. 15, 863.

28. C. H. Dauben and D. H. Templeton, (1955). Acta Cryst., 8, 841.

29. D. H. Templeton, (1960). Univ. of Calif. Lawrence Rad. Lab., Berkeley, Report UCRL 9146, March 1960.

30. D. H. Templeton, (1962). In Int. Tables for X-Ray Cryst., vol. III, Birmingham, Kynoch Press.

31. M. J. Cooper, (1963). Acta Cryst. 16, 1067.

32. D. T. Cromer, (1965). Acta Cryst. 18, 17.

33. L. R. Saravia and S. Caticha Ellis. (1966). Acta Cryst. 20, 927.

34. A. C. Hazell, (1967). Acta Cryst. 23, 1096.

35. D. T. Cromer and D. Liberman, (1970) Los Alamos Sci. Lab., Univ. of Calif., Report LA-4403, UC-34. Also: J. Chem. Phys. 53, 1891.

36. L. G. Parratt and C. F. Hempstead, Phys. Rev., 94, (1954), 1593.

37. R. Parthsarathy, Acta Cryst. 15 (1962), 41.

38. S. R. Hall and E. N. Maslen, Acta Cryst. 20 (1966), 383.

39. P. Harrison, G. A. Jeffrey and J. R. Townsend, Acta Cryst. 11 (1958), 552.

40. J. R. Townsend, G. A. Jeffrey and G. N. Panagis, (1959), Z. Kristallogr. 112, 150.

41. R. B. Roof, (1961). Acta Cryst. 14, 934.

42. S. W. Peterson, (1955). Nature (Lond). 176, 395.

43. S. W. Peterson and H. G. Smith, (1962). Journal Phys. Soc. Japan 17, Suppl. BII, 335.

44. S. Ramaseshan (1966). Curr. Sci. 35, 83.

45. A. C. MacDonald and S. K. Sikka, (1969). Acta Cryst. B25, 1804.

46. S. K. Sikka, (1969). Acta Cryst., A25, 539.

47. S. K. Sikka, (1970). Acta Cryst., A26, 662.

48. S. K. Sikka, (1973). Acta Cryst., A29, 211.

49. P. B. Moon, (1960). Nature, 185, 427.

50. P. J. Black and P. B. Moon, (1960), Nature, 186, 481.

51. P. B. Moon, (1961), Proc. Roy. Soc., A263, 309.

52. H. J. Lipkin, (1961). Phys. Rev., 123, 62.

53. P. J. Black, D. E. Evans and D. A. O'Connor, (1962). Proc. Roy. Soc. A270, 168.

54. P. J. Black, G. Longworth and D. A. O'Connor, (1964). Proc. Phys. Soc., 83, 925.

55. P. J. Black, G. Longworth and D. A. O'Connor, (1964). Proc. Phys. Soc., 83, 937.

56. D. A. O'Connor and P. J. Black, (1964). Proc. Phys. Soc., 83, 941.

57. P. J. Black and I. P. Duerdoth, (1964). Proc. Phys. Soc., 84, 169.

58. P. J. Black (1965) Nature, 206, 1223.

59. G. S. Zhdanov and R. N. Kuz'min, (1968). Acta Cryst. B24, 10.

60. R. Mossbauer, (1974). Naturwissenschaften 60, II, 493.

61. R. J. James, The Optical Principles of the Diffraction of X-rays. (1965 ed.) Cornell Univ. Press, Ithaca, N.Y., Chapt. IV.

62. H. Hönl, Ann. d. Physik, 18 (1933), 625.

63. H. Hönl, Zeit. f. Physik, 84 (1933), 11.

64. J. A. Wheeler and J. A. Bearden Phys. Rev. 46 (1934), 755.

65. H. Bethe, Handb. d. Phys. 24, Berlin: Springer. (1930).

66. H. Einselohr and G. L. J. Muller, (1954). Zeit. f. Phys. 136, 491.

67. Don T. Cromer (1965). Acta Cryst. 18, 17.

68. S. Cohen, (1960). Phys. Rev. 118, 489.

69. D. T. Lieberman, J. T. Waber and D. T. Cromer, (1965). Phys. Rev.

70. J. C. Slater, (1951). Phys. Rev. 81, 385.

71. J. C. Slater, Quantum Theory of Atomic Structure, vol. III, Newton McGraw-Hill (1960).

72. R. Latter (1955). Phys. Rev. 99, 510.

73. International Tables for X-Ray Crystallography (1952) Kynoch Press, Vol. III, Birmingham, England.

74. Y. Cauchois and H. Hulubei (1947) Longuers d'Onde des Emissions X et des Discontinuités d'Absorption X, Paris, Herrmann et Cie.

75. S. Ramaseshan and S. C. Abrahams (eds.). Anomalous Scattering, Proceedings of an Inter-Congress Conference, IUCr, Madrid, April 1974: Munksgaard, Copenhagen, (1975).

Crystallography Matters!