Crystallography Matters!

Resources for crystallographic education

Rotation matrices and translation vectors in crystallography

S. Hovmöller

1. Rotation matrices and translation vectors

Rotation matrices (R) and translation vectors (t) are very powerful descriptions of the symmetry within the crystal and give aid in origin specification, in determining phase restrictions, systematic absences, systematic enhancement and seminvariants, in distinguishing centric and acentric reflections, general and spatial reflections and are helpful in making correct space group determinations.

Every space group has a number of equivalent positions. These may be from 1, as in P1, to 192, as in Fm3m, Fm3c, Fd3m, Fd3m and Fd3c. Every atom at a point (x, y, z) is also found as a result of the symmetry at position ($x^{\prime}, y^{\prime}, z^{\prime}$). The equivalent positions are listed for all space groups in International Tables for X-ray Crystallography. The equivalent positions are related to each other through symmetry operations. Every symmetry operation is a pair of R and t. One equivalent position is derived from another through a rotation and a translation applied in that order. The word rotation stands not only for 2-, 3-, 4- or 6-fold rotation, but also for reflections in a point or in a plane. The translations are along axes or diagonals of the unit cell. The relation between two equivalent positions can be denoted as:

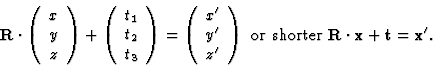\begin{displaymath} \textbf{R} \cdot \left(\begin{array} {c} x\\ y\\ z\end{array... ...\textbf{R} \cdot \textbf{x} + \textbf{t} = \textbf{x}^{\prime}.\end{displaymath} (1)

Example :

The space group P1 has only one equivalent position (x, y, z). The only symmetry operation in that space group is thus the unit matrix, I

\begin{displaymath} \textbf{I} = \left(\begin{array} {ccc}1 & 0 & 0\\ 0 & 1 & 0\... ...textbf{t} = \left(\begin{array} {c}0\\ 0\\ 0\end{array}\right).\end{displaymath}

Example :

The space group P31 has 3 equivalent positions: (x, y, z), (-y, x - y, $\frac{1}{3}$ + z) and (y - x, -x, $\frac{2}{3}$ + z). The symmetry operations are:

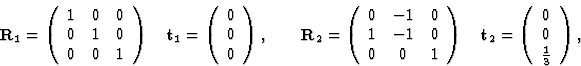
\begin{displaymath} \textbf{R}_1 = \left(\begin{array} {ccc}1 & 0 & 0\\ 0 & 1 & ... ...= \left(\begin{array} {c}0\\ 0\\ \frac{1}{3}\end{array}\right),\end{displaymath}

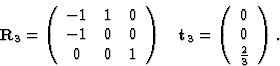
\begin{displaymath} \textbf{R}_3 = \left(\begin{array} {ccc}-1 & 1 & 0\\ -1 & 0 ... ...= \left(\begin{array} {c}0\\ 0\\ \frac{2}{3}\end{array}\right).\end{displaymath}

Note that

\begin{displaymath} \textbf{R}_2 \cdot \textbf{R}_2 = \textbf{R}_3, \textbf{t}_2... ... = \textbf{R}_3 \cdot \textbf{R}_2 = \textbf{R}_1 = \textbf{I}.\end{displaymath}

The different symmetry operations for each space group can always be derived from at the most 3 unique not further reducible symmetry operations (3 because space is 3-dimensional). All other symmetry operations can be derived from the unique ones through:

\begin{displaymath} \textbf{R}_i + \textbf{t}_i = \textbf{R}_m (\textbf{R}_n \{\... ...t}_m) \cdots] + \textbf{t}_0\}\ + \textbf{t}_n) + \textbf{t}_m,\end{displaymath} (2)
where m, n and o can be 1, 2 or 3 for the 3 unique symmetry operations.

2. The structure factor

For every space group and every structure and every reflection (hkl) we know:

\begin{displaymath} F(hkl) = \sum^N_{j=1} f_j \cdot \exp [2{\pi}i(hk_j + ky_j + lz_j)],\end{displaymath} (3)

where

  • F(hkl) is the amplitude and phase for a reflection with indices (h, k, l). F(hkl) is called the structure factor.
  • fj is the scattering factor of atom j.
  • N is the number of atoms in the unit cell.
  • xjyjzj are the x-, y- and z-coordinates of atom j.

In the following (hx + ky + lz) is often written hx to make the formulae shorter.

The structure factor depends on

  • 1. The kinds of atom in the unit cell.
  • 2. The position of the atoms within the unit cell.

Since the space group symmetry gives information about the relative positions of the atoms, F(hkl) will become dependent on the symmetry. This holds both for the phase and amplitude of F(hkl). The form of this dependence will come clear from the following pages.

3. Special reflections

In a space group with n equivalent positions (Rix + ti), i = 1, 2, $\dots$, n the structure factor can be calculated through summing up the contributions to it in the following way:

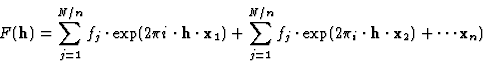\begin{displaymath} F(\textbf{h}) = \sum^{N/n}_{j=1} f_j \cdot \exp (2{\pi}i \cd... ...}_i \cdot \textbf{h} \cdot \textbf{x}_2) + \cdots \textbf{x}_n)\end{displaymath} (4)
i.e. first all the atoms of the first equivalent position are added, then those atoms related to the first ones through R2 + t2 are added, and so on until all atoms within the unit cell are added.

According to (1) every equivalent position can be written as Rx + t. If this expression is inserted into (4), and we for the sake of simplicity look at a space group with 2 equivalent positions, we obtain:

\begin{displaymath} F(\textbf{h}) = \sum^{N/2}_{j=1}f_j \exp (2{\pi}i\textbf{hx}... ...\sum^{N/2}_{j=1} f_j \exp (2{\pi}i\textbf{h}[\textbf{Rx} + t]).\end{displaymath} (5)
The second of these sums can be rewritten, since

\begin{displaymath} \exp (2{\pi}i\textbf{h}[\textbf{Rx} + \textbf{t}]) = \exp (2{\pi}i[h\textbf{Rx} + \textbf{ht}])\end{displaymath}

\begin{displaymath} \phantom{J\exp (2{\pi}i\textbf{h}[\textbf{Rx} + \textbf{t}])} = \exp (2{\pi}i\textbf{hRx} + 2{\pi}i\textbf{ht})\end{displaymath} (6)

\begin{displaymath} \phantom{M=I\exp (2{\pi}i\textbf{h}[\textbf{Rx} + \textbf{t}])} = \exp (2{\pi}i\textbf{hRx})\cdot \exp (2{\pi}i\textbf{ht}).\end{displaymath}

If (5) and (6) are combined we get:

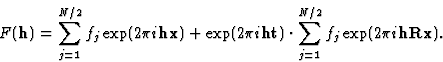\begin{displaymath} F(\textbf{h}) = \sum^{N/2}_{j=1} f_j \exp (2{\pi}i\textbf{hx... ...tbf{ht}) \cdot \sum^{N/2}_{j=1} f_j \exp (2{\pi}i\textbf{hRx}).\end{displaymath} (7)
It is obvious that in the general case the contributions from the two parts of the structure differ, both in amplitude and phase. If, however, the two contributions are equally large, i.e. have identical amplitudes, there will be several interesting situations. The amplitudes of two (or more) parts of the structure are equal if and only if $\textbf{hR}_i = \textbf{h}$ or $\textbf{hR}_i = -\textbf{h}$ for at least one $\textbf{R}_i$, $i \neq 1$.

4. Phase restrictions

In the general case, where the contributions from the two parts of the unit cell have different amplitudes, F(hkl) can be represented as the sum of two vectors of different lengths (= amplitude) and different directions (= phase) as in Fig. 1.

 
Figure 1: The structure factor F(h) = F(hkl) represented as the vector sum of the contributions from two parts of the unit cell. In the general case these two parts differ both in amplitude and phase.
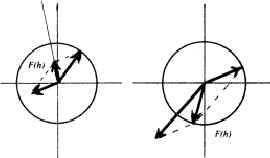\begin{figure} \includegraphics {fig1.ps} \end{figure}

The phase of F(hkl) can take on any value between 0 and 360$^{\circ}$. The special case that $\textbf{hR} = -\textbf{h}$ will result in a restriction of the possible value of the phase of F(hkl). This is called phase restriction. If the phase of the first contribution in (7) is $\alpha$ and ht = 0, then the phase of the second contribution becomes $-\alpha$. As is clear from Fig. 2 the only possible phase values for the sum of these two contributions are 0 and 180$^{\circ}$, or if expressed in radians 0 and $\pi$. If $-90 < \alpha < 90^{\circ}$, the phase of F(hkl) becomes 0$^{\circ}$, and if $90 < \alpha < 270^{\circ}$ the phase of F(hkl) will be 180$^{\circ}$. The phase of Fhkl is denoted $\varphi$ here in order to distinguish it from the phase of the contributions.

 
Figure 2: In the special case where two halves of the unit cell have equal amplitude contribution, but opposite phases ($\alpha$ and $-\alpha$), the resulting reflection will have a phase restriction.
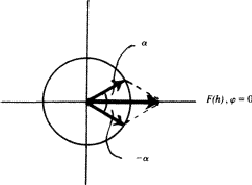\begin{figure} \includegraphics {fig2.ps} \end{figure}

We say (hkl) has a phase restriction of 0 ($\pm$ 180$^{\circ}$).

All reflections in centrosymmetric space groups have phase restriction 0 ($\pm$180$^{\circ}$). Most reflections in non-centrosymmetric space groups lack phase restriction, but some special reflections have phase restriction. The phase is not necessarily restricted to 0 ($\pm$ 180$^{\circ}$) - such phase restrictions as 45$^{\circ}$, 60$^{\circ}$, 90$^{\circ}$ and so on exist. All phase restrictions are $\pm$ 180$^{\circ}$ or modulo 180$^{\circ}$. In order to clarify this an example is worked out in some detail.

What is the phase restriction of (h01) in space group P3121 (No 152)? The equivalent positions are:

\begin{displaymath} (x, y, z),\quad (-y, x - y, \frac{1}{3} + z),\quad (y - x, -x, \frac{2}{3} + z),\end{displaymath}

\begin{displaymath} (y, x, -z),\quad (-x, y - x, \frac{1}{3} - z) \mbox{ and } (x - y, -y, \frac{2}{3} - z).\end{displaymath}

The rotation matrices and translation vectors are:

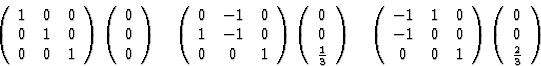
\begin{displaymath} \left(\begin{array} {ccc} 1&0&0\\ 0&1&0\\ 0&0&1\end{array}\r... ...\left(\begin{array} {c}0\\ 0\\ \frac{2}{3}\end{array}\right)\\ \end{displaymath}

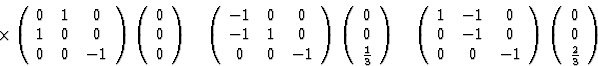
\begin{displaymath} \times\left(\begin{array} {ccc}0&1&0\\ 1&0&0\\ 0&0&-1\end{ar... ...\left(\begin{array} {c}0\\ 0\\ \frac{2}{3}\end{array}\right)\\ \end{displaymath}

While the equivalent positions are derived from the rotation matrices and translation vectors through Rx + t the equivalent reflections are derived through h$^{\prime}$ = hR. While (xyz) was written as a column vector, (hkl) must be written as a row vector.

The reflections equivalent to (hkl) are:

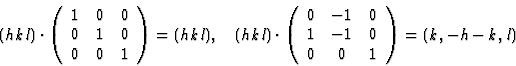
\begin{displaymath} (hkl) \cdot \left(\begin{array} {ccc}1&0&0\\ 0&1&0\\ 0&0&1\e... ...ccc}0&-1&0\\ 1&-1&0\\ 0&0&1\end{array}\right) =(k, -h -k, l)\\ \end{displaymath}

and so on, giving (hkl), (k, h-k, l), (-h -k, h, l), (k, h, -l), (-h -k, k, - l) and (h, -h -k, -l). The reflection (h01) is equivalent to (0, -h, 1), (-h, h, 1), (0, h, -1), (-h, 0, -1) and (h, -h, -1). All these reflections have equal amplitude, but their phases may differ, as we shall see later.

Phase restrictions occur if and only if (hkl) Ri = (-h, -k, -l), that is when the Friedel pair of a reflection is generated by any Ri. If $h \neq 0$ only R5 creates a Friedel pair of (h01).

These results are introduced into (7). If the first summation over half the atoms in the unit cell gives a contribution to the structure factor of amplitude |F| and phase $\alpha$, the other half of the atoms in the unit cell will give a contribution of amplitude |F| but with a phase exp (2$\pi$iht)$\cdot$($-\alpha$). The value exp (2$\pi$iht) is short for exp (2$\pi$i[ht1 + kt2 + lt3]) which in this case equals exp (2$\pi$i[$h \cdot 0 + k \cdot 0 + 1 \cdot \frac{1}{3}$]) or exp (2$\pi$i/3) or +120$^{\circ}$ (note the + sign!). The second sum thus has a phase of 120$^{\circ}$ $-\alpha$. As is clear from the geometrical interpretation in Fig. 3, the resulting structure factor will take on either the phase 60$^{\circ}$ or 240$^{\circ}$.

Figure 3: A reflection with a phase restriction other than 0 or 180$^{\circ}$.
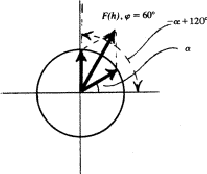
\begin{figure} \includegraphics {fig3.ps} \end{figure}

Reflections with phase restrictions are more often very strong or very weak than general reflections. This is due to the fact that the two contributions are either both large or both small in the case of a phase restricted reflection, whereas in the general case their amplitudes are independent. On the basis of their probability to take on extreme amplitude values all reflections are sorted into two categories: acentric or centric reflections. Reflections without phase restriction are called acentric and reflections with phase restrictions are called centric. The probability distribution of centric and acentric reflections is so different that it is often possible to distinguish between the space groups P1 and $P\overline{1}$ only from intensity data. The concept centric should not be mixed up with centrosymmetric or centred (also spelled centered). While centrosymmetric refers to a space group, centric refers only to single reflections. Although all reflections in centrosymmetric space groups are centric, not all reflections in non-centrosymmetric space groups are acentric.

5. Systematic absences

If h $\cdot$ R = h and h $\cdot$ t $\neq$ 0 (modulo 1) then the reflection h is extinct, or absent, i.e. its amplitude is $\equiv$ 0. If we have a 2-fold symmetry, like in P21, the two contributions to the structure factor are equally large but have exactly opposite directions and they cancel each other. This is illustrated in Fig. 4a. In space groups with 3-fold symmetry, such as P31, there will be systematic absences for reflections where hR = h and h $\cdot$t = $\frac{1}{3}$ or $\frac{2}{3}$, as illustrated in Fig. 4. Because of the 3-fold symmetry the atoms are divided into 3 groups rather than 2 as was the case with a 2-fold symmetry. With 4- or 6-fold symmetry the situation is much like that of the 3-fold, only we now have 4 or 6 contributions, each unlike in size but differing by 90$^{\circ}$ and 60$^{\circ}$ respectively. See Figs. 4c and 4d.

 
Figure 4: The rise of systematic absences in space groups with (a) 2-fold, (b) 3-fold, (c) 4-fold and (d) 6-fold symmetry elements.
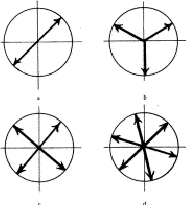\begin{figure} \includegraphics {fig4.ps} \end{figure}

6. Systematic enhancement, epsilon

The third and last case of special reflections is where hR = h and ht = 0 (modulo 1).  The 2 (or 3 or 4 or 6 or more) contributions are equally large and have the same phase and thus enlarge each other. The expected intensity ($I \sim F^2$) of such a reflection is 2 (or 3 or 4 or 6 or more) times as large as that of a general reflection. The factor of enhancement is called epsilon ($\varepsilon$) and is easily derived as the number of rotation matrices Ri that can be applied on h and give back h.

Example :

In P2 there are two symmetry operations:

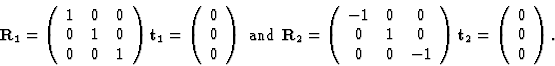
\begin{displaymath} \textbf{R}_1 = \left(\begin{array} {ccc}1&0&0\\ 0&1&0\\ 0&0&... ...f{t}_2 = \left(\begin{array} {c}0\\ 0\\ 0\end{array}\right).\\ \end{displaymath}

All reflections of the type (0 k 0) will fulfil the criteria hR = h and ht = 0 for both the symmetry operations, and thus these reflections have $\varepsilon$ = 2. It is clear that $\varepsilon$ is not the effect of systematic absences. See Fig. 5.

7. Phase shifts

In analogy with equivalent positions, and as an effect of these, there are equivalent reflections. Two equivalent reflections, h and h$^{\prime}$, always have the same amplitudes, i.e. |F(h)| = |F(h$^{\prime}$)|, but their phases may differ. The phases are, however, related to each other in an easily deduced way. The difference in phase between two equivalent reflections is called phase shift. How the phase shift arises and how great it is will be shown now.

Two reflections h and h$^{\prime}$ are equivalent if there exists an Ri such that $\textbf{h}^{\prime} = \pm\textbf{hR}_i$.Due to Friedel's law h is always equivalent to -h. The phases of two equivalent reflections are related as:

\begin{displaymath} F(\textbf{h})^{\prime} = F(\textbf{hR}) = \exp (2\pi i\textbf{ht}) \cdot F(\textbf{h}).\end{displaymath}

Proof :

The proof is carried out for a 2-fold symmetry for the sake of simplicity. A similar strategy can be used for higher symmetries. If x and Rx + t are equivalent positions, then R-1 (x - t) is also an equivalent position, since just as well as x gives rise to x$^{\prime}$, x$^{\prime}$ gives rise to x, by the same symmetry operation:

\begin{displaymath} \textbf{R}^{-1}([\textbf{Rx} + \textbf{t}]-\textbf{t})=\text... ...tbf{Rx})=(\textbf{R}^{-1}\textbf{R})\cdot\textbf{x}=\textbf{x}.\end{displaymath}

R-1 is the inverse matrix of R, i.e. R- 1R=I. We shall make use of this when we calculate F(h$^{\prime}$) = F(hR):
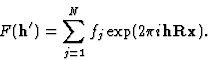\begin{displaymath} F(\textbf{h}^{\prime}) = \sum^N_{j=1} f_j \exp (2{\pi}i\textbf{hRx}).\end{displaymath} (8)
In analogy with (5) we now sum over half the unit cell:
\begin{displaymath} F(\textbf{h}^{\prime}) = \sum^{N/2}_{j=1} f_j \exp (2{\pi}i\... ...2{\pi}i\textbf{hR}[\textbf{R}^{-1}\{\textbf{x}- \textbf{t}\}]).\end{displaymath} (9)
The second sum in (9) is easily simplified to (10) making use of RR- 1 = I.
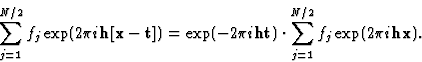\begin{displaymath} \sum^{N/2}_{j=1} f_j \exp (2{\pi}i\textbf{h}[\textbf{x}-\tex... ...extbf{ht})\cdot \sum^{N/2}_{j=1} f_j \exp (2{\pi}i\textbf{hx}).\end{displaymath} (10)
The term exp ($-2{\pi}i$ht) can be brought outside the summation since it is a constant. Note the minus sign of the exponent! We now get
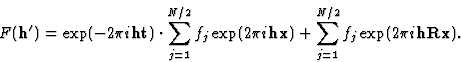\begin{displaymath} F(\textbf{h}^{\prime}) = \exp (- 2{\pi}i\textbf{ht})\cdot \s... ...\textbf{hx}) + \sum^{N/2}_{j=1} f_j \exp (2{\pi}i\textbf{hRx}).\end{displaymath} (11)
(11) is compared to (7):
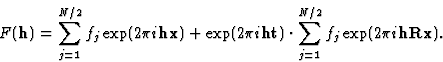\begin{displaymath} F(\textbf{h}) = \sum^{N/2}_{j=1} f_j \exp (2{\pi}i\textbf{hx... ...tbf{ht}) \cdot \sum^{N/2}_{j=1} f_j \exp (2{\pi}i\textbf{hRx}).\end{displaymath} (7)
The two expressions (11) and (7) are identical except for the phase term exp ($-2{\pi}i$hr) which is applied on both sums of (7) in order to get (11). Thus F(h) and F(h$^{\prime}$) have equal amplitudes but differ in phase by exp ($2{\pi}i$ht).

The phase shift is called $S_\textbf{h}$ and is equal to exp ($-2{\pi}i$ht). Note the minus sign!

\begin{displaymath} F(\textbf{h}^{\prime}) = \exp (-2{\pi}i\textbf{ht})\cdot F(\textbf{h}).\end{displaymath} (12)
This is often written in other forms, denoting the phase of $F(\textbf{h}) \varphi (\textbf{h})$:

\begin{displaymath} \varphi(\textbf{h}^{\prime}) = \varphi(\textbf{h}) + S_\text... ...\prime}) = \varphi(\textbf{h}) - 360^{\circ} \cdot \textbf{ht}.\end{displaymath}

Since the phase shift depends on the translation vector, all phases of equivalent reflections derived through symmetry operations with translation vector = 0, are equal. An example of equivalent reflections with different phases will be given. Derive the phases of all reflections equivalent to (h 0 1) in space group P3121. The equivalent reflections were derived in section 4.

\begin{displaymath} (3\,0\,1), (0\,-3\,1), (-3\,3\,1), (0\,3\,-1), (-3\,0\,-1)\,\mbox{ and }\,(3\,-3\,-1).\end{displaymath}

If the first reflection, (3 0 1), is +60$^{\circ}$, then the second becomes

\begin{displaymath} 60^{\circ} - 360^{\circ} \cdot (3 \cdot 0 + 0 \cdot 0 + 1 \c... ...rc} \cdot \frac{1}{3} = 60^{\circ} - 120^{\circ} = -60^{\circ}.\end{displaymath}

In a similar way the phases of the other reflections are 60$^{\circ} - 240^{\circ} = 180^{\circ}, 60^{\circ} - 0^{\circ} = 60^{\circ}, 60^{\circ} - 120^{\circ} = -60^{\circ}$ and $60^{\circ} - 240^{\circ} = 180^{\circ}$.

Note that the fifth reflection ($-3\, 0 -1$) also is the Friedel pair of (3 0 1). Due to Friedel's law the phase of any reflection must be minus that of its Friedel pair. In all cases where a symmetry operation generates an equivalent reflection which is also its Friedel mate, we have two indications of the phase value. If the phase of (hkl) is $\varphi$ then the phase of (-h -k -l) is $-\varphi$ due to Friedel's law, and the phase is $\varphi - S_h$ due to the phase shift. We now have a system of equations:

\begin{displaymath} (- h - k - l) = - \varphi \phantom{+S_h}\end{displaymath}

\begin{displaymath} (-h -k -l) = \varphi + S_h\end{displaymath}

with the solution $-\varphi = \varphi + S_\textbf{h}$,i.e. $\varphi = S_\textbf{h}/2$ (modulo 180$^{\circ}$ since $S_\textbf{h}$ of course is modulo 360$^{\circ}$). This alternative way of deriving phase restrictions is clearly more relevant than that of section 4.

In a similar way the systematically absent reflections can be shown to be exactly those reflections which have two contradictory phase indications. In P21 (0 k 0)-reflections with k odd are extinct. The equivalent positions of P21 are (x, y, z) and ($-x, \frac{1}{2} + y, -z$). The reflections (hkl) and (-h, k, -l) are equivalent and the phase shift is k/2. A reflection like (0 3 0) is thus equivalent to itself, but the equivalent reflection generated has a phase differing from the original one by 180$^{\circ}$. The phase of (0 3 0) is at the same time $\varphi$ and $\varphi + 180^{\circ}$, which of course is only possible if the amplitude of the reflection is 0!

Suggestions for further reading

Hall, S. R., Symmetry Considerations in the Application of the Structure Invariants. Nato Advanced Study School on Direct and Patterson Methods, Parma, Italy (1970).

Luzzati, V., The Use of Statistical Methods for the Detection of Symmetry Elements. International Tables for X-ray Crytallography, Vol. II, pp. 355-356. Birmingham, Kynoch Press (1959).

Main, P., On Defining the Origin and Enantiomorph, in M. M. Woolfson (ed.), Direct Methods in Crystallography (Lecture Notes), York (1974).

Rogers, D., The Probability Distribution of X-ray Intensities. IV. New Methods of Determining Crystal Classes and Space Groups, Acta Cryst. 3 (1950) 455-464. Statistical Properties of Reciprocal Space, in J. S. Rollett (ed.), Computing Methods in Crystallography London, Pergamon Press (1965).

Sheldrick, G. M., Structure Factor Algebra, in International School of Crystallography (Lecture Notes). V. Course. Direct Methods of Solving Crystal Structures. Part 1. Erice, Director Prof. G. Allegra. (1978).