Towards a classification of icosahedral viruses in terms of indexed polyhedra
The standard Caspar–Klug classification of icosahedral viruses and Twarock’s Penrose-like characterization of strains not obeying the Caspar–Klug rules are special cases of an approach based on polyhedra having vertices indexed by icosahedral lattice points. Icosahedral rotations combined with scalings leaving the icosahedral lattice invariant (linear, planar, and 3-dimensional) permit edge, face and vertex decoration. In the last case satellite polyhedra are attached to the vertices of a central polyhedron. In all cases the whole is generated from a set of points with rational indices.
A. Janner



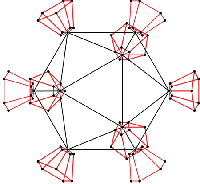 Icosahedron with vertices decorated by truncated pentagonal pyramids. The generating points are at [600000], [711111] and [111333]. This decoration could be a model for viruses with protruding proteins like the spiroplasma virus.
Icosahedron with vertices decorated by truncated pentagonal pyramids. The generating points are at [600000], [711111] and [111333]. This decoration could be a model for viruses with protruding proteins like the spiroplasma virus.


