Statistical descriptors in crystallography
Recommendations
It is not realistic to expect that a statistical procedure can prevent or identify careless work. Thus, published lattice constants with reasonably small s.u.s may be grossly in error, owing to a variety of causes (cf. Parrish, 1960). Only independent redeterminations may show this. Thoughtless use of established procedures in widely distributed software may be as harmful as the natural tendency of most people to prefer results in agreement with preconceived ideas. Note, however, that preconceived ideas are an ingredient of Bayesian statistics. Since the precision may be evaluated with greater confidence than the accuracy, it is not surprising that the results of independent determinations of the same structure may differ by much more, and hardly ever by less than is allowed by statistical tests. Inter-determination goodness-of-fit values can give an indication of the average discrepancies to be expected (Taylor & Kennard, 1986). The following recommendations are intended to produce more meaningful results from structure determinations:
- All reflections to be used in the refinement process should be measured more than once, preferably in more than one symmetry-equivalent position. A fixed length of time allotted to an experiment is better used for rapid measurement of symmetry-equivalent reflections or for integrated intensity measurements made at different values of the azimuthal angle, than for more precise measurements limited to a single independent portion of reciprocal space (Ibers, 1967; Hamor, Steinfink & Willis, 1985). (It should be noted that additional measurements on a different crystal using perhaps a different radiation can also be very revealing concerning the accuracy of refined parameters.)
- If possible, the shape of the sample crystal should routinely be measured and absorption corrections applied.
- Standard uncertainties of the intensities should not be based on counting statistics alone. They should at least take into account the variation of several periodically measured check reflections, which indicate a possible minimal value of k in (20). In the case of averaged intensities, differences among absorption-corrected symmetry-equivalent data and measurements at different values of the azimuthal angle can be used in the estimation. It is an act of faith to assume that these differences are equivalent to random fluctuations, but the uncertainty can be no less than that inferred from this assumption.
- Measured and calculated values of I, |F|2 or |F|, with s.u.s for all measured values should be provided to referees. Any serious discrepancies between measured and calculated values should be noted and commented upon in the text. Calculated values need not be deposited.
- S.u.s of derived quantities like angles and bond lengths should be calculated using the full variance-covariance matrix of the refined parameters. The programming effort and additional calculation time necessary for a full variance-covariance propagation-of-uncertainty analysis are very well rewarded by greatly improved standard uncertainties. In some cases, e.g. in the presence of pseudo-symmetry, the use of the full variance-covariance matrix must even be considered mandatory.
- All intensities or structure amplitudes should be included in the refinement. Omitting weak reflections often has little effect on the results (Seiler, Schweizer & Dunitz, 1984; Wang, Barton & Robertson, 1986). However, weak reflections may contain important information: they may be vitally important when a choice is to be made between a centrosymmetric and a non-centrosymmetric model (Marsh, 1981, 1986), and when refining superstructures. Intensities measured as negative may be left negative in the refinement (Hirshfeld & Rabinovich, 1973). Setting them to zero (after averaging) is advocated with the argument that even a perfect model cannot reproduce negative intensities. They may also be set to positive values by a Bayesian procedure (French & Wilson, 1978). For further discussion of weak reflections see the section Refinement on I, |F|2 or |F|?.
- It is of utmost importance to resolve any space group ambiguities, and in particular to ascertain the presence or absence of a center of symmetry. The methods for doing this fall into two classes:
(i) Modern statistical tests operating on diffraction data
Tests based on the Wilson (1949) statistics using complete sets of intensity data perform remarkably well for structures containing a large number of not too dissimilar atoms which occupy general positions in the asymmetric unit of the space group. An additional requirement is the absence of non-crystallographic symmetry.
Approximate methods which may cope with the presence of outstandingly heavy atoms were brought to a form applicable to all space groups by Shmueli & Wilson (1981) and Shmueli & Kaldor (1981, 1983). In practice, these methods may fail for some low-symmetry structures with extreme atomic heterogeneities.
Exact probability distributions of structure amplitudes which are formulated as Fourier series and can be computed to any precision, are now available for low-symmetry space groups (Shmueli, Weiss, Kiefer & Wilson 1984; Shmueli & Weiss, 1987). They allow for hypercentric distributions (Shmueli, Weiss & Kiefer, 1985), and for heavy scatterers in special position (Shmueli & Weiss, 1988). These methods account correctly for any atomic heterogeneity.
(ii) Measurement of symmetry-dependent physical properties
These properties include crystal morphology, etch figures, optical activity, pyroelectricity and piezoelectricity (International Tables for Crystallography, 1983), which generally require the availability of single crystals with no linear dimension less than about 2 mm. The most powerful and discriminating test rests upon detection of the generation of second harmonics, see for example Dougherty & Kurtz (1976). This method requires only the availability of a microcrystalline sample. All these methods may reveal the absence, but not the presence of a center of symmetry. - Although multiplication of the elements of the variance-covariance matrix of the model parameters by the square of the goodness of fit, S2, leads to conservative estimates of standard uncertainties, since S tends to be greater than 1.0, this practice is based on the questionable assumption that the variances of the observations by which the weights are assigned are relatively correct but uniformly underestimated. Should S lie outside the range expected at the given confidence level, then either the weights or the model or both are suspect. In particular, the uncertainties of the measurands I, |F|2 or |F| are usually not uniformly underestimated; all known type A and type B uncertainty components should be carefully estimated and included in (W2). Publications should indicate whether standard uncertainties assigned to structural parameters refined by least squares have been multiplied by S. The value of S must be reported.
- Reliability indices like R, wR and goodness of fit S give a global measure of fit. They are not well suited for testing certain properties of the structure, such as polarity, absolute configuration or the presence of a center of symmetry. An improved global fit obtained by modifying one of these properties represents also all concomitant changes of the refined parameters and may not indicate the correctness of the modification. Rather, the property should be represented by a single refineable parameter, whose refined value and s.u. is much more indicative. This has been successfully done for the determination of absolute configuration and polarity (Rogers, 1981; Flack, 1983).
- In IUCr publications, the term estimated standard deviation (e.s.d.) should be replaced, in all statements of the statistical uncertainties in data and in estimates of the values of the measurands, by the term standard uncertainty (s.u.), symbol u. When it is necessary to make it clear that the uncertainty estimate contains several components, the term combined standard uncertainty (c.s.u.), symbol uc, should be used. In formulae concerned with statistics, the symbol
 shall be used to represent the positive square root of the variance of a usually unknown probability distribution, and the symbol s shall be used to represent the positive square root of a sample estimate of the variance
shall be used to represent the positive square root of the variance of a usually unknown probability distribution, and the symbol s shall be used to represent the positive square root of a sample estimate of the variance  2 (s is also called the experimental standard deviation, and s/
2 (s is also called the experimental standard deviation, and s/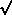 N is called the experimental standard deviation of the mean of N sample estimates).
N is called the experimental standard deviation of the mean of N sample estimates). -
When reporting the result of a measurement and its uncertainty, the experiment must be thoroughly documented to include the following information:
(a) a clear description of the methods used to calculate the measurement result and its uncertainty from the experimental observations and other data;
(b) a list of all uncertainty components and their evaluation;
(c) a presentation of the data analysis in such a way that each of its important steps can be followed and the calculation of the reported result can be independently repeated; and
(d) a list of all factors and constants used in the analysis and their sources (e.g. atomic scattering factors, linear absorption factor, monochromator polarisation ratio, etc.).Of particular importance in crystallographic structure determination is a thorough and complete description of data-reduction procedures used to convert observed Bragg and background intensities into |F|2 and |F| values. It is preferable to provide too much information rather than too little.
- The numerical value of an estimate y and its standard uncertainty u(y) should not be reported with an excessive number of digits. However, y should be quoted with sufficient accuracy to minimize the effect of round-off error* in subsequent calculations. In order to limit the round-off error of y (denoted by e) to 25% of u(y), u(y) should be quoted to two significant digits in the range 10 to 19, implying that corresponding digits also be quoted for y, and to one significant digit in the range 2 to 9. In general, uncertainties should be rounded up rather than to the nearest digit. For example, a bond distance of 1.54249 Å with a s.u. of 0.01532 Å should be reported as 1.542(16) Å (e = 3%), and one of 2.16352 Å with a s.u. of 0.00481 Å should be reported as 2.164(5) Å (e = 10%). Correlation coefficients should normally be quoted with two significant figures unless their absolute value is close to the value of 1.0 in which case three significant figures should be used.
- Restraints, e.g. on distances, angles and displacement parameters, are observations supplementary to the diffraction data with uncertainties that may be of type B. They affect the goodness of fit S and the uncertainties of the refined parameters. They must be reported in as much detail as the diffraction data.
[Previous]
* If u(y) is reported by a one- or two-digit, number, denoted by s that corresponds to the final digits in the value of y, then the largest round-off error of y is e = (50/s)% of u(y). Thus, for s = 1, e = 50%. In some fields of science (e.g. high-energy physics), it common practice to limit the maximum round-off error to 5%, which amounts to quoting u(y) always as a two-digit number (10
 s
s  99). In addition to recommendation 12, the IUCr admits this practice as an option.
99). In addition to recommendation 12, the IUCr admits this practice as an option.
© 1989, 1995 International Union of Crystallography
Updated 23rd Sept. 1996
These pages are maintained by the Commission Last updated: 15 Oct 2021

