Statistical descriptors in crystallography
Glossary of statistical terms
Accuracy: The closeness of agreement between the value of an estimate, derived from a physical measurement, and the true value of the quantity (measurand) estimated. The reference to the true value implies that in practice accuracy cannot be exactly evaluated. The terms accuracy and precision must not be confused. Experimental science endeavours to gain insight into physical reality (or truth) through interpretation of measurements using models. This is based on the implicit assumption that a bad agreement between observations and the corresponding calculated model quantities indicates inaccuracy (see Goodness of fit); the converse of this proposition, that good agreement between observations and model quantities indicates accuracy, is thereby not implied. A model that does not take into account all available evidence and prior experience may give apparently precise, but inaccurate (wrong) results.
Average: The average of a set of values {xi}, 1 
i n, is defined by <x> = (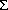 
i xi)/n. If the {xi} are a sample of n independent observations of a single quantity x distributed according to a probability density function p(x) with mean µ and variance 
2, <x> is a minimum-variance unbiased estimate of µ ; s2 = [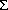i (xi - <x> )2]/(n - 1) is an unbiased estimate of 2. The variance of the probability density function of <x> is 2/n and an unbiased estimate is obtained from s2/n. These estimates do not require a complete knowledge of p(x) to be available. Using a set of weights {wi}, the weighted average is defined by <xw> = 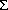i wixi/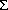i wi. If the {wi} do not depend on the {xi}, <xw> is an unbiased estimate of µ. The weighted average finds its use in cases where the n observations are drawn from populations of identical mean but differing variances.
Bayesian: An interpretation of probability developed from Bayes's theorem [Bayes, 1763; see Probability density function, equation (17), and Basic notions]. Bayes's theorem itself is accepted by either frequentist or Bayesian statisticians. However, the assignment of prior probabilities in Bayesian inference has caused much discussion. Bayes's postulate assumes an equipartition of ignorance and states that in the absence of information to the contrary all prior probabilities are assumed to be equal. The work of Jaynes (1983), on the other hand, shows that by using the concepts of group invariance uninformative prior probabilities may be obtained which are far from the uniform distributions suggested by a casual appreciation of Bayes's postulate. At the present time, many Bayesian statisticians would contend that the search for uninformative prior probabilities is misguided since some prior knowledge of the system studied is always available.
Bias: An estimator of a statistical quantity is biased if the expected value of the quantity is not equal to the true value. In the physical sciences, bias is usually considered as synonymous with systematic error. In statistics, it is sometimes restricted to a particular type of systematic error, arising from the mathematical model applied to the observations. Any non-linear operation or model can result in a bias, as for example taking the square root of an intensity when computing structure amplitudes. The bias is then due to the fact that the expected value of a function f(x) is in general not a simple function of the expected value of x:
(1) . . E [ f (x)]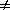 
f [E (x)]
The equality will hold for any distribution of x if f(x) is a linear function of x. Biases in this restricted sense are proportional to the variances due to random errors of the observations (Wilson, 1976b).
Combined standard uncertainty (c.s.u.): Standard uncertainty of the result of a measurement when that result is obtained from the values of a number of other quantities through a functional relationship (W1). It is calculated from the corresponding component uncertainties, and is the positive square root of the combined variance uc2(y) obtained from (W2). The calculation of combined standard uncertainties of measurands refined by least squares is described in the section on refinement. In mathematical formulae, the term is symbolized by uc.
Conditional probability density function: see Probability density function.
Correlation: see Moment.
Covariance: see Moment.
Cumulative distribution function (c.d.f.): The function P(x) obtained by integration of the continuous probability density function (p.d.f.) p(t):
(2) . . P (x) = -infx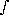
p(t) dt.
Degrees of freedom: When m parameters are estimated from n observations (n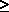 
m), the quantity n - m is called the number of degrees of freedom for error.
Deviance: If Oj are the observed values, and Cj the corresponding calculated model values of n quantities, the differences dj = Oj - Cj are called deviates. The definition holds for any given choice of model parameters (see Residual). The deviance between the calculated and observed quantities is
(3) . . Do = 
j=1n(O j - Cj)2 = j=1nd j2.
The weighted deviance is
(4) . . Dw = j=1nk=1n(O j - Cj) (Ok - Ck) = dTWd,
where d is an n vector of deviates. The positive-definite n x n weight matrix W may be written as a product W = BTB. The matrix B is not in general uniquely defined and may be specified for example as an upper-triangular matrix, or alternatively as a symmetric matrix. Equation (4) then becomes Dw = dTBTBd, where Bd is the vector of weighted deviates. If correlation terms of W are assumed to be negligible, W becomes a diagonal matrix, and the quantity commonly refined in least squares is obtained:
(4') . . Dw = j=1n wj (Oj - Cj)2.
The weighted deviates are then dj = wj1/2 (Oj - Cj). If the weights are the reciprocals of the variances of the observed quantities, wj = j-2, or more generally W = V-1, where V is the variance-covariance matrix of the observations, the weighted deviance is often called the scaled deviance. For maximum likelihood, the scaled deviance is -2 ln Lmax.
Durbin-Watson d statistic: d quantifies the serial correlation of least-squares deviates. In its original form it is defined by
(5) . . d = j=2N (dj - dj-1)2 / j=1N dj2,
where dj = Oj - Cj is the deviate. d takes values 0 < d < 4. For no serial correlation a value close to 2 is expected. With positive serial correlation, adjacent deviates tend to have the same sign, and d becomes less than 2, whereas with negative serial correlation (alternating signs of deviates) d takes values larger than 2. Tables of values for testing d are given by Durbin & Watson (1950, 1951, 1971) and a convenient approximation to the tables based on the normal distribution is provided by Theil & Nagar (1961). Clearly the sequencing of the observations is important in the evaluation of d. For a least-squares fit where the value(s) of d are significantly different from 2, the estimates of the variances and covariances of the parameters can be grossly in error, being either too large or too small. The serial correlation of the deviates may arise from a time dependence of the observations [e.g. time series; Flack, Vincent & Vincent (1980)], from an experimental correlation of the observations [e.g. gas electron diffraction; Morino, Kuchitsu & Murata (1965); Murata & Morino (1966)] or, most importantly in crystallography, from inadequacy in the physical model used in the least-squares fit [e.g. Rietveld analysis; Hill & Flack (1987)]. The most general form of d is given by
(5') . . d = (dTBTPB d) / (dTW d)
where d, W and B are defined in the section Deviance, P is an n x n matrix with Pjk = 2, for | j - k | = 0, Pjk = -1, for | j - k | = 1, and Pjk = 0 for | j - k | > 1, and BTB = W.
Error: The difference between the result of a measurementt and the true value of a measurand. It is a measure of accuracy. Because the true value of the measurand is in principle unknowable, the error is also unknowable. In presenting a result it is implicitly assumed that the measurement model includes all known effects [see equation (W1)], and that appropriate tests for the detection of unsuspected systematic errors have been performed (see Goodness of fit, Model, Systematic error, Defects in the model and Prince & Spiegelman, 1992). All contributions to the model are sources of uncertainty, which may be type A or type B according to the method used for their evaluation.
Estimate: A value of a physical quantity obtained from the observations by use of an estimator. The quantities usually estimated in crystallography are lattice parameters, and atomic positional and displacement parameters.
Estimated standard deviation (e.s.d.): An estimate of the standard deviation, or square root of the variance, of a probability density function. Methods used for obtaining e.s.d.s of diffraction intensities may take into account quantum counting statistics, the variations of periodically measured check reflections, and the scatter among symmetry-equivalent reflections. Such methods are part of the model, and not of the observations. Note especially recommendation 10.
Estimator: A mathematical expression (function) leading from the observations to an estimate of the value of a physical quantity. An estimator is unbiased if its expected value is equal to the true value of the quantity (see Model). In the presence of bias in the restricted sense which is proportional to the variances due to random errors of the observations, the expected value of the estimator changes with observation time, and converges to the unbiased value (in the restricted sense) for an eternal immutable experiment.
Expected value: Defined as
(6) . . E [f (x)] = -inf+inf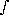 f (x) p (x) dx
for the function, f(x), of a random variable x whose probability density function is p(x). E[f(x)] is not a function of x, but it does depend on p(x). Expectation is a synonym of expected value. The expected value of x, E(x), is called the mean of the probability density function and is often denoted by µ.
Gaussian: see Normal probability density function.
Goodness of fit: A measure of the extent to which calculated model values Cj of a set of n quantities (e.g. X-ray intensities) approach the observed values Oj. In the statistical literature, the term denotes a class of hypothesis tests. For a crystallographic least-squares refinement with weight matrix W, it is defined as the square root of the weighted deviance divided by its expected value:
(7) . . S2 = dTW d/E(dTW d).
The deviation of S2 from unity is a measure of the validity of the model used to compute Cj, and of the estimate of the variance-covariance matrix V of the observations used to calculate E(dTW d). If, and only if, the weight matrix W in the refinement is chosen to be the inverse of V, W = V-1, then E(dTW d) = n - m, regardless of the form of the p.d.f. (Wilson, 1980b); m is the number of variables in the model, and n - m the number of degrees of freedom. For a diagonal matrix V, S2 becomes then
(7') . . S2 = (n - m)-1 n j-2(Oj - Cj)2.
Further for the W = V-1 weighting scheme, if the deviates are normally distributed (i.e. with Gaussian joint p.d.f.), the value of S2 that will be exceeded in 100
% of replications is given by
(8) . . (S2) = 
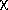2n - m, / (n - m),
where 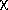2n-m, is the 100% point of the 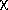2 distribution. See Abrahams (1969) for a fuller discussion, including calculation of the expected range of S2 at a given confidence level. It is common practice among crystallographers refining parameters by least squares to multiply the corresponding standard uncertainties by S. This questionable practice is equivalent to the assumption that a lack of fit is due entirely to an underestimate of the variances of the observations, whose relative values have been correctly assigned.
Maximum likelihood: If the m vector x is a set of parameters, and the n vector y is a set of observations, the conditional probability density function pC(y | x) can be considered to be a density function for x giving the likelihood of observing y. It is written L(x | y). The method of maximum likelihood finds the maximum of L as a function of x. It is often simpler to work with the natural logarithm, ln L. Maximum likelihood is equivalent to least squares for a normal distribution of errors and to Bayesian estimation using a uniform prior distribution.
Mean: term used for the expected value of x, E(x), of a probability density function p(x).
Measurand: Particular quantity subject to measurement. In most cases a measurand Y is not measurable directly but depends on other measurable quantities, which themselves may be viewed as measurands, through some functional relationship (W1). Measurands of interest to crystallographers include atomic coordinates, bond lengths and displacement tensors.
Measurement: Set of operations having the object of determining a value of a quantity.
Model: Conjecture about physical reality used to interpret the observations. An estimator is constructed using the mathematical formulation of the model. In crystallography, the observations usually are integrated intensities and associated backgrounds, but may also include other information, e.g. crystal dimensions. The standard model is kinematical X-ray or neutron diffraction by a crystal composed of spherical atoms or point nuclei undergoing harmonic displacements. The term 'corrected observations' leads to confusion. Any correction applied to the observations is part of the model, and results in a quantity which has not been observed. This includes all data-reduction procedures to obtain structure amplitudes, including absorption and Lorentz-polarization corrections and averaging of symmetry-equivalent data. Thus, structure amplitudes are not observed quantities. For the sake of computational efficiency, corrections without adjustable parameters may be applied to the observations in a data-reduction procedure. However, any non-linear process, e.g. taking the square root, may result in additional bias.
Moment: The expected value of the nth power, xn, of the random variable x is called the nth moment of the probability density function (p.d.f.) p(x):
(9) . . E (xn) = -inf+inf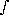 xn p (x) dx
The first moment or mean is commonly denoted by E(x) = µ. The second moment about the mean, E[(x - µ)2], is the variance of p(x) and is commonly denoted by 2. In a space of n dimensions, the mean of the joint probability density function pJ(x) is an n vector E(x) with elements µi = E(xi) equal to the mean of the marginal p.d.f. of xi. The n x n variance-covariance matrix (tensor of rank 2 in n dimensions) is defined by the second moments about the mean:
(10) . . Vij = E[(xi - µi)(xj - µj)] = 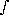(xi - µi)(xj - µj)pJ( x)dn(x).
For i = j, this is equal to the variance of the marginal p.d.f. of xi, Vii = i2. The correlation matrix is defined by
(11) . . rij = Vij /(ij),
-1 rij 1 and rii =1. The set of Mth moments of pJ(x), E[x1m(1)x2 m(2).....xnm(n)] with m(1) + m(2) + ... + m(n) = M, transforms as a totally symmetric tensor of rank M in n dimensions.
Normal (Gaussian) probability density function: A probability density function of the quantity x with standard deviation about the mean µ, given by
(12) . . p(x) = -1 (2
)-½ exp {-½[(x - µ)/]}.
The normal probability density function can originate from addition of a large number of small and independent errors, each with its own non-normal distribution, but occurrence of a normal p.d.f. does not imply this underlying structure. The standard normal deviate z = (x - µ)/ has a normal distribution with zero mean and unit standard deviation, when x is distributed according to (12).
Normal probability plot: A graphical procedure in which the differences between two independent sets of measurements, or those between experiment and theory, are analyzed in terms of a normal (Gaussian) p.d.f. The ordered experimental normal deviates or order statistics such as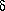 
mi = (O(1)i - kO(2)i)/[u2(1) i + k2u2(2)i] ½ where O(1) and O(2) are independent observations with standard uncertainties u(1) and u(2) of the same quantity obtained in separate experiments and k is a scale factor, or 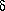Ri = (Oi - Ci)/ui (see Goodness of fit), are plotted against the ordered standard normal deviates. A resulting normal probability plot that is linear, with zero intercept and unit slope, shows that the experimental deviates are normally distributed (Abrahams & Keve, 1971; Hamilton & Abrahams, 1972; Hamilton, 1974). The 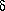R plot is a more powerful statistical descriptor than the traditional single-valued discrepancy index R = | Oi - Ci | / Oi.
Order statistic: When a sample of variate values are arranged in order of magnitude, these ordered values are known as order statistics.
Parameter: Models are formulated in terms of physical quantities called parameters, values for which are estimated from the observations. The true (unknown) value of a parameter is a constant, since it represents a physical fact independent of the observations. Any estimate of its value is a random variable. In the framework of Bayesian statistics, a parameter (not its estimate) is regarded as a random variable and the associated p.d.f. is taken to represent the scientist's belief in the value of the parameter.
Population: see Random variable.
Precision: The closeness of agreement between the values of a measurement or of an estimate obtained by applying a strictly identical experimental procedure several times. It is expressed numerically by a standard deviation or variance. The precision of a diffraction intensity is often inferred from only one, or maybe two measurements by (1) invoking Poisson statistics for the count rates, and/or (2) using the experience gained from earlier diffraction experiments. Precise estimates are not necessarily accurate (Prince, 1985; Rollett, 1985).
Probability density function (p.d.f.): The function p(x) of the random variable x, such that the probability of finding x between a and b (a < b) is given by
(13) . . P ( a x b) = ab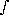 p(x) dx.
The probability of finding x somewhere within the whole interval of variation is equal to unity.
Consider an ordered set, or n vector, of n random variables x = (x1x2....x n). The joint (or multivariate) p.d.f. of x is the function pJ(x), such that
(14) . . P ( a1 x1 b1, . . . , an xn bn) = a1b1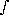 . . . anbn 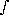pJ(x) dnx.
The marginal p.d.f. pM(xi) of an element xi of x is the p.d.f. of that element irrespective of the values of any other elements:
(15) . . pM(xi) = 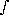pJ(x) dn-1x.
where the integration is over the full range of all elements except xi. If pJ(x,y) denotes the combined joint p.d.f. for the elements of two vectors x and y, the conditional p.d.f. for x given y, pC(x | y), is the joint p.d.f. of the elements of x when the elements of y are held at fixed particular values. It is related to the joint p.d.f. of x and y by
(16) . . pC(x | y) = pJ(x,y)/pM(y).
Therefore, pJ(x,y) = pC(x | y)pM(y) = pC(y | x)pM(x) from which it follows that
(17) . . pC(x | y) = pC(y | x)pM(x)/pM( y).
This last relation is known as Bayes's theorem. If pC(x | y) = pM(x) for all possible values of y, the random variables x and y are statistically independent.
Random error: An error having a zero expected value. Particularly important in crystallography are statistical fluctuations in quantum counts. Other effects like irreproducible play in diffractometer settings, and short-term fluctuations of temperature, pressure, mains voltage (Abrahams, 1969) and humidity contribute, at least in part, to the random errors. Random errors can be reduced at the expense of increased measuring time. If the model and the method of refinement are perfect, errors of estimated parameters are also random (see Bias).
Random variable: The possible outcomes of a measurement. The set of all possible outcomes is a population. The set of outcomes of a finite number of repeated measurements is a sample drawn from the population.
Repeatability: The closeness of the agreement between the results of successive measurements of the same measurand carried out under the same conditions, namely the same method of measurement, the same observer, the same measuring instrument, the same location, and repetition over a short period of time.
Reproducibility: The closeness of agreement between the results of measurements of the same measurand where the individual measurements are carried out changing conditions such as method of measurement, observer, measuring instrument, location, time.
Residual: A general term denoting a quantity remaining after some other quantity has been subtracted. It occurs in a variety of contexts. For example, the term residual has been used by crystallographers to mean the discrepancy index R. In a different sense, if the calculated value of a variable is subtracted from an observed value then the difference may be called a residual, although the more precisely defined term deviate is to be preferred. Some authors restrict it to mean only those deviates obtained from least squares at convergence, but terms such as 'deviates at convergence' or 'residuals at convergence' would avoid possible confusion.
Sample: see Random variable.
Scaled deviance: see Deviance.
Standard deviation: The square root of the variance of a probability density function.
Standard uncertainty (s.u.): Uncertainty of the result of a measurement expressed as a standard deviation. In mathematical formulae, the term is symbolized by u.
Systematic error: Contribution of the deficiencies of the model to the difference between an estimate and the true value of a quantity. A list of important systematic errors in measured X-ray intensities has been given by Abrahams (1969). The systematic errors can be reduced by improving the model, but not by an investment in measuring time. In some cases, their presence can be inferred from the goodness of fit, from normal probability plots (Abrahams, 1974), from the distribution of scaled deviates (Oj - Cj)/uj as functions of O, C, sin
/
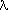, diffractometer angles, etc., or by using the Durbin-Watson statistics (Flack, 1984, 1985) to reveal correlations. Some systematic errors (e.g. an incorrect value of the wavelength) cannot be detected by any statistical test. The amount of systematic error present in any estimate cannot be evaluated exactly (see Accuracy). Note that, strictly speaking, observations are free of systematic error, in contrast to the model used for their interpretation (see Estimator).
Type A evaluation of uncertainty: Method of evaluation of uncertainty by the statistical analysis of a series of observations.
Type B evaluation of uncertainty: Method of evaluation of uncertainty by means other than the statistical analysis of a series of observations.
Uncertainty (of measurement): A parameter, associated with the result of a measurement, that characterizes the dispersion of the values that could reasonably be attributed to the measurand. It gives an indication of the lack of exact knowledge of the value a measurand, not to be confused with the term error. Categorizing uncertainty into type A and type B components avoids possible ambiguity inherent in a categorization into random and systematic components.
Suggested translations of the English terms uncertainty and standard uncertainty are: Unbestimmtheit, Standardunbestimmtheit in German; incertitude, écart type in French; neopredelønnosth, standartnaå neopredelønnosth in Russian.
Variance: The second moment about the mean (see Moment) of a probability density function.
Variance-covariance matrix: The n x n matrix whose elements are the second moments about the mean of a joint probability density function of n random variables [see (10)].
Weight: Value used to express the relative importance of an observation (e.g. an intensity) with regard to the quantities to be deduced from the data set (e.g. atomic positional coordinates). Weights appear in averaging, least squares, statistics (e.g. Goodness of fit) and elsewhere. For a set of n data the weights are represented by an n x n weights matrix W. Usually, W is taken to be diagonal. In averaging and least squares, minimum-variance estimates are obtained by W = V-1 where V is the variance-covariance matrix of the observations.
Weighted deviance: see Deviance.
© 1989, 1995 International Union of Crystallography
Updated 23rd Sept. 1996
These pages are maintained by the Commission Last updated: 15 Oct 2021