Statistical descriptors in crystallography
Weighting schemes
A very commonly used criterion for the choice of weights is that the variance of the derived estimates be minimal, although other weighting schemes are permissible. The minimum-variance criterion implies that W = V-1. Regardless of the choice of weights, proper calculation of standard uncertainties and of the goodness of fit in intensity averaging and in least squares will require an estimate of V, the variance-covariance matrix of the observations. The frequentist and Bayesian approaches to statistics lead to different interpretations of V (see section on Refinement). For the one, V is concerned only with the random fluctuations of the measurements whereas, for the other, V also incorporates the scientist's belief in the model with which the observations are being analysed.
Weights of averaged intensities
Minimum-variance weights can at best be based on estimated standard deviations (standard uncertainties) of intensities. In many cases, n symmetry-equivalent corrected net intensities Ii = ciOi will be averaged, where the ci will contain at least the scan speeds and absorption corrections. Weights used in averaging should not be based on the counting statistics of the individual observations whose estimated variances are biased and result in larger weights for accidentally low intensities, and lower weights for accidentally high intensities. Owing to the symmetry postulated while averaging, the expected values of all corrected intensities Ii , E(Ii), must be the same quantity µI, and the expected values of the observed intensities Oi are thus(19) . . E(Oi) = µI /ci.
An often used expression for the uncertainty of Oi (Abrahams, 1974) is
(20) . . u2(Oi) = E(Oi) + bi + kE(Oi)2
= µI /ci + bi + kµI2/c i2,
where bi is the contribution of the background estimated from peak and background count rates, and kE(Oi)2 is the contribution from known and unknown sources of random error. Minimum variance weights u-2(Ii) = {ciu(O i)}-2 needed for the calculation of the average intensity can be obtained by iteratively replacing µI by an approximate average value <I>. In a first step, bi and k may be neglected and the average intensity then becomes
(21) . . <I> =  (Ii/ci) /
(Ii/ci) /  (1/ci) =
(1/ci) =  Oi /
Oi /  (1/ci).
(1/ci).
Estimates of the factor k in (20) can be obtained from the variations of periodically measured check reflections. Differences among symmetry-equivalent intensities can (and indeed should) also be used to estimate k, the value of which then includes at least part of an anisotropic systematic error. A possible procedure consists in adjusting k to obtain comparable values for the variance of estimated from the u2(Ii) derived from (20), and estimated from the spread of the Ii around the average value <I>:
(22) . . u2(<I>) 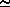 1 /
1 /  n u-2 (Ii)
n u-2 (Ii)
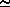 [
[  n u-2 (Ii) { Ii -<I> }2 ] / [ (n - 1)
n u-2 (Ii) { Ii -<I> }2 ] / [ (n - 1)  n u-2(Ii) ];
n u-2(Ii) ];
u(Ii) = ciu(Oi); n 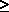 2.
2.
The average goodness of fit of all symmetry-equivalent sets is then near 1·0. If the number n of symmetry-equivalent observations is large, the larger of the two estimates of u(<I>) obtained with some approximation for u2(Ii), their average, or the value from the spread alone may be used. Alternative and more convenient procedures, variants and extensions may be proposed, or have already been implemented (see also Blessing, 1987).
Weights based on the model
The theory of least squares shows that expected values of parameter estimates are not affected by the choice of weights, provided that the model is free of systematic error (i.e. the estimator is unbiased), and the weights are not functions of the deviates dj = Oj - Cj (Prince & Nicholson, 1985; Prince, 1985; 1989). On the other hand, weights based on dj, Oj or Cj may result in a bias. As remarked before, uncertainties of the observations are usually estimated from the observations themselves. In particular, the contribution of counting statistics to the uncertainty of an intensity is proportional to the intensity itself. An accidentally low intensity will have a lower uncertainty than an accidentally high intensity, showing that this estimate of the uncertainty is indeed biased. The corresponding weights may result in bias in the parameter estimates. Wilson (1976b) investigated the effect by assuming that the weight of a deviate is an arbitrary function of the corresponding measured and/or calculated quantity, wj = wj(Oj, Cj). He showed that in case of refinement of one parameter, the use of the weighted mean wj({Oj + 2Cj}/3) removes this bias to the order of the mean square statistical fluctuation of the measurement. Weights from equation (20) and (22) may be functions of all intensities, and the corresponding bias is then more difficult to evaluate.The omission of observations is equivalent to assigning zero weights. Again, a bias may be introduced if the criterion for omission is based on dj, Oj or Cj. Thus, if weak reflections are systematically omitted, those with an accidentally low intensity will be preferentially discarded, and those with an accidentally high intensity will have a better chance of being retained. An example of such a bias has been described by Seiler, Schweizer & Dunitz (1984). Omission of observations according to sin /
/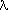 or reflection number should not result in a bias.
or reflection number should not result in a bias.
Weight modification schemes designed to lessen the effects of systematic errors are necessarily based on the deviates dj. An example is found in Wang & Robertson (1985). They estimate the variances of the structure amplitudes from the distribution of the weighted deviates. The resulting weights are intended to represent all kinds of random errors from different sources, but include also contributions of systematic errors. The robust/resistant refinement techniques are another example. The results of a standard least-squares refinement may be considerably influenced by 'outliers', observations that seem so discrepant with calculated values that a blunder of the investigator or a malfunctioning of the equipment is suspected. The naive approach to such observations is to discard them by setting the weights to zero whenever the discrepancy exceeds a certain limit. The robust/resistant methods avoid the discontinuity of this procedure by decreasing the weights gradually with increasing disagreement (Prince, 1982; Nicholson, Prince, Buchanan & Tucker, 1982).
Restraints
Restraints or soft constraints are relations between parameters of the model that are treated formally in the same way as observations (Waser, 1963; Hendrickson & Konnert, 1980; Hendrickson, 1985). They may be used to specify bond lengths, angles, planarity of molecules, relations between displacement parameters, and for numerous other purposes. The uncertainties attributed to such pseudo-observations are chosen according to the scientist's beliefs regarding their validity, in agreement with the Bayesian interpretation of statistics. S.u.s of the parameter estimates are, of course, dependent on these variances. It may be difficult to judge whether they are appropriate if they are recorded in a structure data file omitting all information regarding the restraints.Enhancing particular features
A minority of Subcommittee members believes in the merit of weighting schemes chosen to enhance particular features of the structure. These weights then reflect the scientist's aims rather than the precision of the measurements. A more demanding method would consist in altering the experimental design to correspond more closely to the objectives of the study. Prince & Nicholson (1985) address the problem of finding the reflections that should be measured more precisely in order to enhance particular features.Obtaining an unweighted least-squares fit between observed and calculated |F|2 is equivalent to obtaining an unweighted least-squares fit between observed and calculated Patterson functions. Similarly, obtaining an unweighted least-squares fit on the |F|s is almost equivalent to obtaining an unweighted least-squares fit between observed and calculated electron densities (Wilson, 1976a).
Special weighting schemes permit more accurate fitting of the electron densities at the atomic sites. Thus, Cochran (1948, 1951) showed that refinement on the |F|s with weights inversely proportional to the reciprocal of the atomic scattering factor of an atom gives the coordinates of the maximum of its electron density as represented by a Fourier series. In the presence of several types of atoms, weighting with the reciprocal of a mean scattering factor is probably a satisfactory approximation. Similarly, the weighting scheme of Dunitz & Seiler (1973) designed to determine more accurately the coordinates of the atomic centers also emphasizes high-order reflections.
Bernardinelli & Flack (1985) have designed weights that enhance the sensitivity of a refinement to the centrosymmetric or antisymmetric parts of the electron density, and also to the absolute structure. They are useful in resolving ambiguities between centro- and non-centrosymmetric structures and mainly affect weak reflections, the importance of which in such problems has been pointed out by Marsh (1981, 1986). Weak reflections are also critically important in the refinement of superstructures, and weighting schemes are easily designed to enhance their contribution to the normal equations.
© 1989, 1995 International Union of Crystallography
Updated 23rd Sept. 1996
These pages are maintained by the Commission Last updated: 15 Oct 2021

