Pourquoi les groupes de symétrie en cristallographie
D. Weigel
(A) Cristal parfait - définition du reseau - exemples
On définit habituellement le cristal parfait comme un objet infini engendré par la répétition triplement périodique d'un motif central remplissant tout le volume convexe (0, a, b, c) appelé alors maille centrale.
On a défini ici un cristal parfait à trois dimensions si a, b, c sont trois vecteurs linéairement indépendants (c'est-à-dire non contenus dans un même plan) de l'espace à 3 dimensions. Les vecteurs qui répètent infiniment ce motif sont les vecteurs
![]()
où u, v et w sont des entiers relatifs (négatifs, positifs ou nuls) quelconques, chacun d'entre eux pouvant parcourir le groupe Z des entiers relatifs (u, v, w ).
Exemples : Pour simplifier, tous nos exemples sont donnés dans l'espace à 2 dimensions, à l'aide de dessins de tapisseries recouvrant le mur d'une chambre (de dimensions infinies puisqu'il s'agit d'un cristal parfait).![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif)
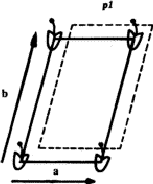
- ler exemple Fig. 1: la maille est un parallèlogramme, le réseau sera appelé réseau oblique. Ce parallèlogramme ne contient qu'une fleur par maille![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif) et pour cette raison le réseau est dit primitif.
et pour cette raison le réseau est dit primitif.
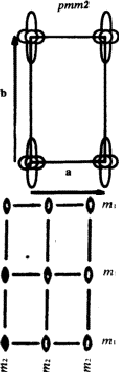
- 2ème exemple Fig. 2: la maille est un rectangle contenant une seule fleur, le réseau est appelé rectangle primitif.
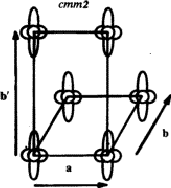
- 3ème exemple Fig. 3: cette fois nous avons le choix entre deux réseaux: le réseau a, b oblique primitif. Le réseau a, b![]() rectangle centrée,
rectangle centrée,![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif) appelé ainsi parce qu'il contient deux fleurs par maille et que si l'on choisit l'origine de la maille au centre d'une fleur le centre de la seconde fleur est au centre du rectangle.
appelé ainsi parce qu'il contient deux fleurs par maille et que si l'on choisit l'origine de la maille au centre d'une fleur le centre de la seconde fleur est au centre du rectangle.
Remarque : l'origine 0 de la maille est arbitraire et on peut la choisir n'importe où, cf. Fig. 1 où la meme maille décalée est dessinée en pointillé.
Théorème : pour un cristal parfait, les vecteurs t forment un groupe de translation![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif) qui définit le réseau.
qui définit le réseau.
Démonstration : La loi de composition est l'addition et c'est une loi de composition interne dans l'ensemble des vecteurs t. L'ensemble des vecteurs t contient l'élément neutre u = v = w = 0. Chaque vecteur t a un inverse contenu dans l'ensemble t: ![]() . Cet ensemble constitue donc un groupe.
. Cet ensemble constitue donc un groupe.
Exemples
- pour le trois exemples précédents, si on choisit la maille a, b on a:
![]()
- pour le troisième exemple, si on choisit la maille a, b![]() on a:
on a:
![]()
et la restriction u + v = 2p (pair)
Dans tous le cas le groupe des vecteurs t définit le réseau et précise si celui-ci est primitif (pas de restriction), centré ![]()
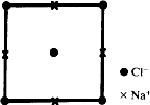
Remarque : ces dessins qui nous ont servi de modèles ne sont pas tellement éloignés de la réalité: si on considère la section de la structure de NaCl par le plan de la face de sa maille cubique on obtient
- soit la Fig. 4 si on ponctualise les ions en ne représentant que leurs noyaux
- soit la Fig. 5 si on représente plus correctement les courbes d'egale densité electronique![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif) qui ressemblent quelque peu aux lignes des contours des fleurs dessinées sur les Figs 1, 2, 3
qui ressemblent quelque peu aux lignes des contours des fleurs dessinées sur les Figs 1, 2, 3
Définitions mathématiques du réseau et de la maille dans le cas d'un cristal parfait (facultatif)
Soit l'espace pointé (E, 0) où E est l'espace affine à trois dimensions associé à l'espace vectoriel E à trois dimensions et O est un point de E appelé origine de l'espace pointé (0 est un point arbitraire du cristal).
Les points du cristal sont les éléments de E. Les vecteurs t sont des éléments particuliers de E qui constituent un sous ensemble de E.
Théorème : les vecteurs t forment un groupe infini, dit groupe de translations (démonstration immédiate).
Definition: relation d'équivalence T entre les points A et ![]() de E. On définit la relation d'équivalence suivante: A et
de E. On définit la relation d'équivalence suivante: A et ![]()
![]() E sont équivalents par la relation T si
E sont équivalents par la relation T si
![]()
Cette relation est réflexive, symétrique et transitive. Cette definition nous conduit au résultat suivant.
L'ensemble quotient E/T est constitué de tous les points situés dans le volume convexe (0, a, b, c) emphappelé maille centrale.
Pour le cristallographe les points ![]()
![]()
![]() , appartenant à la même classe d'équivalence, s'identifient à un seul et même point; celui de la maille centrale, p. e.
, appartenant à la même classe d'équivalence, s'identifient à un seul et même point; celui de la maille centrale, p. e.
(B) Cristal parfait: la maille - les groupes ponctuels de symétrie G.P.S. - les positions de Wyckoff - necessité d'introduire les G.P.S. en cristallographie
Définition : la maille est l'ensemble des points (éléments de E) contenu dans le volume convexe (0, a, b, c), c'est-à-dire l'ensemble quotient E/T.
(1) Cas du réseau primitif
Pour simplifier on considère d'abord uniquement le cas du réseau primitif qui est celui en Fig. 1 et 2, où on trouve une seule fleur par maille (4 situées aux 4 coins qui comptent pourCas de la Fig. 1: On a une fleur par maille et on doit la dessiner entièrement pour définir une maille, donc tout le cristal.
Cas de la Fig. 2: On a une fleur par maille mais il suffit de n'en dessiner qu'un quart, par exemple ![]() , si on précise que dans le rectangle maille de la Fig. 2 (i) on a des axes de rotation d'ordre 2 (rotations 0,
, si on précise que dans le rectangle maille de la Fig. 2 (i) on a des axes de rotation d'ordre 2 (rotations 0, ![]() ) aux coins de la maille, aux milieux des côtés et des centres de celle-ci; (ii) on a des plans de symétrie, ou miroirs, qui se projettent orthogonalement sur le côté de la maille et sur les droites parallèles aux côtés passant par le centre. Cf. Fig. 2
) aux coins de la maille, aux milieux des côtés et des centres de celle-ci; (ii) on a des plans de symétrie, ou miroirs, qui se projettent orthogonalement sur le côté de la maille et sur les droites parallèles aux côtés passant par le centre. Cf. Fig. 2
on note bien que pour le cristallographe les quatre quarts de fleur hachurés sont strictement équivalent et ne constituent qu'un seul et même objet de l'ensemble quotient E/T qu'on appelle la maille.
On est donc conduit à rechercher les opérations ponctuelles de symétries (O.P.S.) qui laissent une fleur inchangée. Il s'agit d'isométries ponctuelles , opérations qui conservent les longeurs, ainsi que le centre de la fleur.
On raisonne par exemple, sur la fleur située en 0 et on trouve quatre O.P.S.:![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif)
e , 1![]() identité représentée par la matrice
identité représentée par la matrice 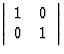 à déterminant + 1
à déterminant + 1
2, la rotation ![]() représentée par la matrice
représentée par la matrice 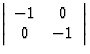 à déterminant + 1
à déterminant + 1
m1, la symétrie par rapport à Ox représentée par la matrice 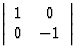 à déterminant -1
à déterminant -1
m2, la symétrie par rapport à Oy représentée par la matrice 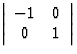 à déterminant -1
à déterminant -1
Théorème : ces quatre O.P.S. (ou les matrices orthogonales 2 ![]() 2 qui leur correspondent) constituent un groupe ponctuel de symétrie (G.P.S.), d'ordre 4 et noté 2mm.
2 qui leur correspondent) constituent un groupe ponctuel de symétrie (G.P.S.), d'ordre 4 et noté 2mm.
Démonstration : établissons la table de multiplication
- la multiplication est une loi de composition interne dans l'ensemble e, 2, m1, m2
- chaque élément est lui même son propre inverse
- le produit de deux éléments différents de e donne le troisième élément différent de e
- il s'agit donc d'un groupe isomorphe au groupe de Klein
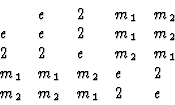
ceci signifie que dans un cristal à deux dimensions dont le G.P.S. est 2mm, chaque fois qu'on précise un point du contour de la fleur par ses coordonnées xy on sait qu'il y a forcément trois autres points dont les coordonnées sont![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif)
![]() ,
, ![]() ,
, ![]() .
.
Definition : l'ensemble de ces quatre points s'appelle les 4 positions générales de Wyckoff du cristal et il y a évidemment isomorphisme entre les quatre transformations
![]()
et les quatre O.P.S. du G. P. S. 2mm: e, 2, m1, m2.
Conclusion : sauf dans un cas particulier comme celui de la Fig. 1 où le G.P.S. du cristal se réduit à l'O.P.S. identité, il est donc indispensable de connaitre le G.P.S. d'un cristal , c'est-à-dire les O.P.S. qui conservent globalement le motif constituant la maille (ensemble quotient E/T) d'un réseau primitif. Les O.P.S. sont donc obligatoirement des isométries ponctuelles.![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif)
Il suffit alors de décrire un quart de la maille (dans le cas de 2mm) pour la connaitre toute .
Dans les cristaux réels on a des atomes ou des ions. On peut d'abord simplifier le problème en le ponctualisant![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif) sur leur noyau qu'on assimile à un point. Si le G.P.S. du cristal est 2mm (supposons qu'il s'agisse d'une monocouche chimisorbée, véritable cristal à deux dimensions) cela signifie que si un atome d'oxygène est en position générale de Wyckoff (x et y
sur leur noyau qu'on assimile à un point. Si le G.P.S. du cristal est 2mm (supposons qu'il s'agisse d'une monocouche chimisorbée, véritable cristal à deux dimensions) cela signifie que si un atome d'oxygène est en position générale de Wyckoff (x et y ![]() 0) on a forcément 4 atomes d'oxygène dans la maille et les positions des trois autres sont impérativement fixées par la position du premier. Dans le quart de maille il suffira donc de préciser la position d'un nombre fini de noyaux d'atomes ou d'ions.
0) on a forcément 4 atomes d'oxygène dans la maille et les positions des trois autres sont impérativement fixées par la position du premier. Dans le quart de maille il suffira donc de préciser la position d'un nombre fini de noyaux d'atomes ou d'ions.
Si on veut être plus précis il faudra établir dans le quart de la maille une carte de densité électronique à partir de laquelle on déduit immédiatement la densité électronique dans les trois autres quarts de la maille.
(2) Cas du réseau non primitif
C'est celui de la Fig. 3: il s'agit d'un réseau rectangle centré. Le G.P.S. du cristal est évidemment le même que pour la Fig. 2, soit 2mm. Mais il suffit maintenant de dessiner le huitième de la maille pour obtenir tout le cristal. En effet on a deux fleurs pour une maille rectangulaire (0, a, b![]() ).
).
Il y a toujours 4 positions générales de Wyckoff, les mêmes; seul le groupe de translation constitué par l'ensemble des vecteurs E diffère. On prend le groupe
![]()
Il ya donc dans ce cas deux vecteurs t par maille alors qu'il n'y en avait qu'un pour la Fig. 2.
Remarque : la maille (ab) avec b = a + b![]() /2, cf. Fig. 3, a l'avantage d'être primitive, mais le grave inconvénient d'être incompatible avec la présence de deux miroirs orthogonaux. Le réseau
/2, cf. Fig. 3, a l'avantage d'être primitive, mais le grave inconvénient d'être incompatible avec la présence de deux miroirs orthogonaux. Le réseau![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif)
![]() est un réseau de Bravais. Le réseau
est un réseau de Bravais. Le réseau ![]() n'en est pas un.
n'en est pas un.
Exercice : Dessiner sur une Fig. 3![]() tous les axes d'ordre 2 et les miroirs (y compris les miroirs avec glissement: symétrie par rapport à un plan suivie d'une translation diviseur d'un vecteur t) présents dans la maille rectangle centré.
tous les axes d'ordre 2 et les miroirs (y compris les miroirs avec glissement: symétrie par rapport à un plan suivie d'une translation diviseur d'un vecteur t) présents dans la maille rectangle centré.
(C) Application des groupes ponctuels de symétrie - propriétés des cristaux - un exemple: ferroélectricité-transition: ferroélectrique 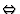 paraélectrique
paraélectrique
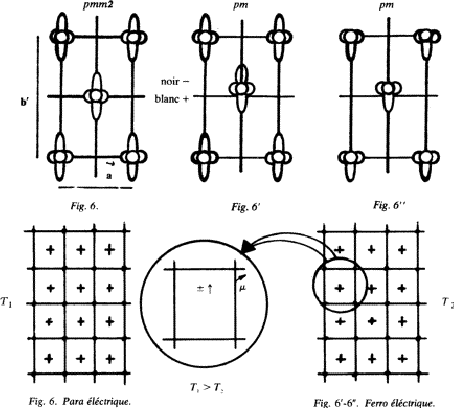
Considérons maintenant le réseau de la Fig. 6:
Il contient des fleurs noires chargées négativement et situées au coin des mailles rectangles; et des fleurs blanches chargées positivement et situées au centre des mailles. On vérifie immédiatement que les G.P.S. de ce cristal est toujours 2mm. Dans ce cas, contrairement à la Fig. 3, les deux fleurs de la maille (la noire et la blanche) no sont plus équivalentes et le motif dont la répétition périodique engendre le cristal n'est plus une fleur, mais l'ensemble des deux fleurs: une noire et une blanche située à ![]() de la noire. Le réseau n'est donc plus centré comme sur la figure 3 mais primitif. Dans chaque maille le centre de gravité des charges positives coincide avec le centre de gravité des charges négatives et le cristal ne présent donc pas de moment dipolaire électrique permanent:
de la noire. Le réseau n'est donc plus centré comme sur la figure 3 mais primitif. Dans chaque maille le centre de gravité des charges positives coincide avec le centre de gravité des charges négatives et le cristal ne présent donc pas de moment dipolaire électrique permanent:![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif) il s'agit d'un composé paraélectrique.
il s'agit d'un composé paraélectrique.
Maintenant si nous acceptons de perdre deux des quatres opérations ponctuelles de symétrie (O.P.S.) du G.P.S. 2mm, en no conservant que e et m2, on peut alors déplacer la fleur blanche en la faisant glisser un peu parallelement à m2.![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif) On obtient alors le cristal de la Fig. 6
On obtient alors le cristal de la Fig. 6![]() dont le G.P.S. est m, groupe d'ordre 2 (e, m2).
dont le G.P.S. est m, groupe d'ordre 2 (e, m2).
Dans chaque maille, si le centre de gravité des charges négatives est toujours au centre du rectangle, le centre de gravité des charges positives en est légèrement décalé vers le haut sur le grand axe du rectangle. Le cristal présente alors un moment dipolaire électrique ![]() que nous avons représenté sur une maille sur les Figs 6
que nous avons représenté sur une maille sur les Figs 6![]() et 6
et 6![]() : il s'agit alors d'un composé ferroélectrique.
: il s'agit alors d'un composé ferroélectrique.
On vérifie immédiatement que si la structure d'un cristal à deux dimensions contient des axes binaires (ou axes 2), pour le cristal supposé infini, les traces de ces axes binaires seront confondues avec les centres de gravité des charges positives et des charges négatives. Le cristal est donc parélectrique. D'où la première loi:
1ère loi: dans un espace à deux dimensions, pour qu'un cristal soit ferroélectrique, il est nécessaire qu'il ne contienne pas de centres de symétrie.
Exercise : généraliser aux axes d'ordre n et démontrer la 2ème loi.
2ème loi: dans une espace à trois dimensions pour qu'un cristal soit ferroélectrique, il est nécessaire qu'il ne contienne pas de centres de symétrie .
La manière dont nous avons introduit la ferroélectricité dans le cristal de la Fig. 6![]() à partir du cristal paraélectrique de la figure 6 justifie immédiatement la 3ème loi.
à partir du cristal paraélectrique de la figure 6 justifie immédiatement la 3ème loi.
3ème loi: lors de la transition paraélectrique ![]() ferroélectrique d'un composé la phase ferroélectrique a un G.P.S. (groupe ponctuel de symétrie) qui est un sous-groupe du G.P.S. de la phase paraélectrique qui est donc la plus symétrique. En effet le G.P.S. m (e, m2) est un sous-groupe du G.P.S. 2mm (e, 2, m1, m2).
ferroélectrique d'un composé la phase ferroélectrique a un G.P.S. (groupe ponctuel de symétrie) qui est un sous-groupe du G.P.S. de la phase paraélectrique qui est donc la plus symétrique. En effet le G.P.S. m (e, m2) est un sous-groupe du G.P.S. 2mm (e, 2, m1, m2).
Facultatif : la 3ème loi est d'ailleurs un cas particulier de la 4ème loi: lors d'une transition ordre-désordre la phase ordonnée est la moins symétrique et son groupe est un sous-groupe de celui de la phase désordonnée.
Il est vrai qu'il peut s'agir ici de groupes spatiaux de symétrie qui seront définis au paragraphe suivant.
Lors de la transition la phase ferroélectrique est-elle la phase haute température ou bien la phase basse temperature?
En pratique le cas de la Fig. 6![]() peut se produire lorsque les fleurs noires sont des gros ions négatifs et les fleurs blanches de petits ions positifs qui ont trop de place dans la cavité formée par les ions negatifs autour.
peut se produire lorsque les fleurs noires sont des gros ions négatifs et les fleurs blanches de petits ions positifs qui ont trop de place dans la cavité formée par les ions negatifs autour.
L'ion positif se déplace alors, par exemple, vers le haut de ces cavités trops grandes dans chaque maille et le composé devient ferroélectrique. Il est bien évident que l'agitation thermique (donc le désordre) ne favorise pas la ferroélectricité: en effet l'amplitude des vibrations thermiques fait hésiter l'ion positif entre les positions excentrées possibles dans la cavité (ici la haute et la basse) et le mantient finalement, en moyenne, dans le temps, au centre de la cavité. La phase paraélectrique (désordonnée) est donc en général la phase haute température, la phase ferroélectrique étant la phase basse température.
(D) Groupes spatiaux de symétrie - principe de Neumann
Lorsque la structure du cristal contient uniquement (en plus des translations du réseau) des O.P.S, (c'est-à-dire qu'il n'y a pas de rotations hélicoïdales ou de réflexions avec glissement), comme c'est le cas pour les structures bidimensionelles représentées sur les Fig. 6 et 6![]() , le groupe spatial de symétrie est défini de la façon suivante:
, le groupe spatial de symétrie est défini de la façon suivante:
Definition: Groupe spatial de symétrie (G.S.S.). Dans ce cas, le G.S.S. est le produit du G.P.S. du cristal par le groupe de translations qui définit son réseau (cf. (A) Théorème). Ainsi dans le symbole du G.S.S. on retrouve le symbole du réseau suivi de celui du G.S.S. Exemples:
![]()
On remarque que le G.P.S. est un groupe fini alors que le groupe de translations et le G.S.S. sont des groupes infinis. Mais la symétrie du cristal peut être engendrée à partir de glismiroirs.
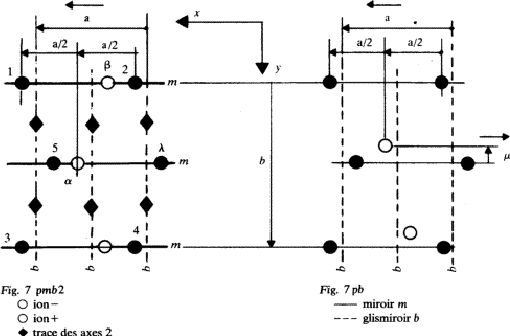
Définitions: glissymétrie--glismiroir . Symétrie par rapport à un plan suivi d'une translation parallèle à ce plan, appelé glismiroir.
Exemple : sur la Fig. 7 les plans se projettant sur les traits pointillés sont des glismiroirs avec la translation b/2; on les nomme pour cette raison glismiroirs b; En effet on passe des boules noires 1 à 5 par glissymétrie avec la translation b/2![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif) on passe d'ailleurs des boules
on passe d'ailleurs des boules ![]() à
à ![]() par la même opération.
par la même opération.
Chaque boule blanche est au centre d'un rectangle formé par 4 boules noires (ainsi ![]() au centre de 1, 2, 3, 4) et réciproquement comme dans le cas de la figure 6 ou chaque fleur blanche était au centre d'un rectangle formé par 4 fleurs noires et réciproquement. Il y a donc une analogie entre les structures des Figs 6 et 7, mais, dans ce dernier cas, le G.S.S. est p mb2 au lieu de p mm2 pour la figure 6 puisque les miroirs m2 ont été transformés en glismiroirs b.
au centre de 1, 2, 3, 4) et réciproquement comme dans le cas de la figure 6 ou chaque fleur blanche était au centre d'un rectangle formé par 4 fleurs noires et réciproquement. Il y a donc une analogie entre les structures des Figs 6 et 7, mais, dans ce dernier cas, le G.S.S. est p mb2 au lieu de p mm2 pour la figure 6 puisque les miroirs m2 ont été transformés en glismiroirs b.
L'opération de symétrie b ne laisse aucun point du cristal inchangé: mb2 n'est donc pas un G.P.S. mais il a été engendré par le G.P.S. mm2 où m a été remplacé par le glismiroir b.
On dit donc que le G.P.S. du cristal de la Fig. 7 (de G.S.S. p mb2) est mm2. Comme pour la figure 6 on montre que la structure de la figure 7 est paraélectrique: en effet, on vérifie immédiatement que, si on considère une maille les centres de gravité des charges positives et des charges négatives coincide avec le centre de la maille.
Maintenant passons de la structure 7 a la structure 7![]() en déplaçant légèrement les boules blanches parallèlement à 0y, comme nous étions passés de la structure 6 à 6
en déplaçant légèrement les boules blanches parallèlement à 0y, comme nous étions passés de la structure 6 à 6![]() .Nous perdons alors les O.P.S. m et 2, et le G.S.S. de la structure 7
.Nous perdons alors les O.P.S. m et 2, et le G.S.S. de la structure 7![]() n'est plus p mb2, mais p b.
n'est plus p mb2, mais p b.![[*]](https://www.iucr.org/__data/assets/image/0008/13310/foot_motif.gif) En effet b est la seule opération de symétrie qui reste en dehors de l'identité.
En effet b est la seule opération de symétrie qui reste en dehors de l'identité.
De plus la structure devient ferroélectrique (comme la structure 6![]() ) avec un moment dipolaire
) avec un moment dipolaire ![]() dont la valeur est proportionelle au déplacement des ions positifs entre les structures 7 et 7
dont la valeur est proportionelle au déplacement des ions positifs entre les structures 7 et 7![]() . Sur cet exemple on justifie donc le principe de Neumann:
. Sur cet exemple on justifie donc le principe de Neumann:
Les éléments de symétrie de toute propriété physique d'un cristal doivent inclure les éléments de symétrie du groupe ponctuel de symétrie de ce cristal (ou groupe au centre du cristal). En effet les translations ajoutées par les glismiroirs (ou par les axes hélicoïdaux dans l'espace à trois dimensions) s'ajoutent aux translations du réseau sans modifier en aucune façon les propriétés physiques du cristal.
On aurait pu présenter ces notions de façon plus rigoureuse: introduire par exemple les G.P.S. comme les sous-groupes du groupe orthogonal, démontrer qu'il n'y a que 32 G.P.S. cristallographiques![]() Pour cette présentation consulter: Cristallographie et structure des solides, tome I, Algèbre et géométrie cristalline et moléculaire, D. Weigel, Masson, Paris 1972.
Pour cette présentation consulter: Cristallographie et structure des solides, tome I, Algèbre et géométrie cristalline et moléculaire, D. Weigel, Masson, Paris 1972.
Pour la symétrie des propriétés physiques des cristaux consulter: Nye, Propriétés physiques des cristaux, Paris.
- ...parfait).
- En chimie physique lorsqu'un cristal supposé sans défaut atteint une dimension de 1
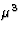 (avec une forme approximativement cubique, ou sphérique) on peut le considérer comme parfait; 1
(avec une forme approximativement cubique, ou sphérique) on peut le considérer comme parfait; 1 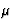 étant une grande longueur devant la longueur a, b , ou c en général 5 à 10 Å.
étant une grande longueur devant la longueur a, b , ou c en général 5 à 10 Å.
- ...maille
- Chacune des 4 fleurs situées aux 4 coins de la maille appartient à 4 mailles et ne doit etre complétée que pour
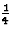 dans la maille centrale.
dans la maille centrale.
- ...centrée,
- ab
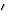 est un réseau de Bravais parce qu'il a le maximum d'angles droits, ab n'en est pas un.
est un réseau de Bravais parce qu'il a le maximum d'angles droits, ab n'en est pas un.
- ...translation
- C'est un groupe infini.
- ...electronique
- Les contours équiprobables pour respecter le langage de la mécanique quantique.
- ...sont
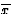 signifie -x; xyz sont les coordonnées relatives du point M: OM =
signifie -x; xyz sont les coordonnées relatives du point M: OM = 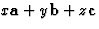 .
.
- ...O.P.S.:
- Sur les Figs 2, 2
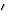 on raisonne dans l'espace à deux dimensions.
on raisonne dans l'espace à deux dimensions.
- ...ponctuelles.
- Opérations qui conservent les longeurs ainsi qu'un point du sous espace affine constitué lar le motif maille.
- ...ponctualisant
- En utilisant le facteur de diffusion atomique.
- ...réseau
- c signifie 'centré'; p signifie primitif.
- ...permanent:
- On rappelle que, so on raisonne sur une seule maille, chaque fleur noire compte pour
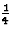 puisque chacune est située au coin de 4 mailles adjacentes, alors que chaque fleur blanche compte entièrement.
puisque chacune est située au coin de 4 mailles adjacentes, alors que chaque fleur blanche compte entièrement.
- ...m2.
- On peut aussi lui arrancher la pétale du haut ou du bas, comme sur la Fig. 6
 , chaque fleur n'étant plus symétrique que par rapport à m2.
, chaque fleur n'étant plus symétrique que par rapport à m2.
- ...b/2
- Si on fait une deuxième fois l'opération, on aboutit à la boule 3; le passage de 1 à 3 est la translation b, vecteur
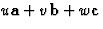 particulier avec u = w = 0 et v = 1; la puissance deux d'une glissymétrie est donc une translation qui ne peut être que b si le miroir est axial, c'est-à-dire parallèle à y (ou a si parallèle à x). La translation de la glissymétrie axiale parallèle à b ne peut donc être que b/2.
particulier avec u = w = 0 et v = 1; la puissance deux d'une glissymétrie est donc une translation qui ne peut être que b si le miroir est axial, c'est-à-dire parallèle à y (ou a si parallèle à x). La translation de la glissymétrie axiale parallèle à b ne peut donc être que b/2.
- ...b.
- Bien entendu le G.P.S. de ce cristal est m.