[Date Prev][Date Next][Thread Prev][Thread Next][Date Index][Thread Index]
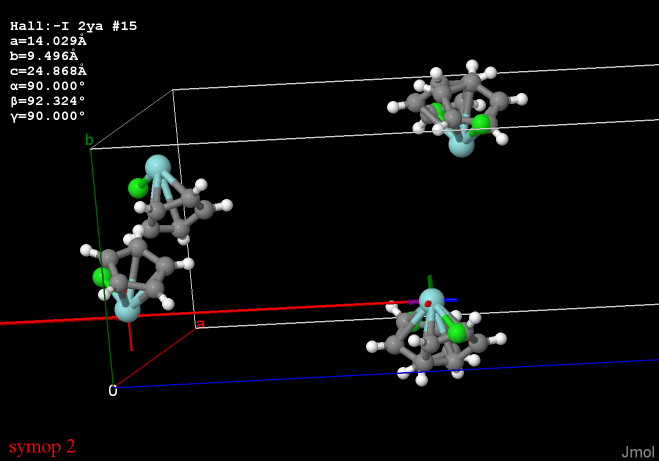
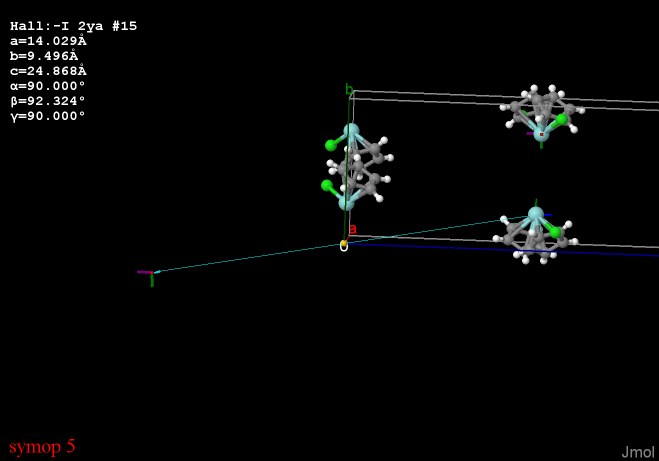
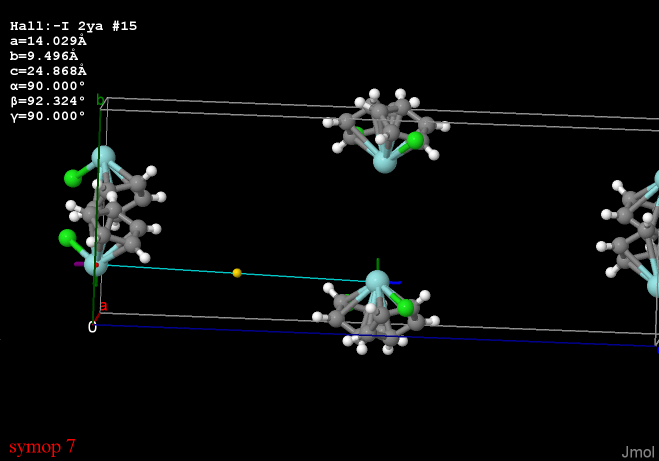
Do we even know if, in any given unit cell, half of the sites are of one complement and half are of the other? Or is it that we know that on average this must be true? How does that work?
[Send comment to list secretary]
[Reply to list (subscribers only)]
Re: Ambiguity in atom_site.disorder_group value -1
- To: Distribution list of the IUCr COMCIFS Core Dictionary Maintenance Group<[email protected]>
- Subject: Re: Ambiguity in atom_site.disorder_group value -1
- From: Robert Hanson via coreDMG <[email protected]>
- Date: Mon, 17 Oct 2022 21:50:44 -0500
- Cc: Robert Hanson <[email protected]>
- In-Reply-To: <CH2PR04MB6950EEBF6DFE85F62D0B644EE0299@CH2PR04MB6950.namprd04.prod.outlook.com>
- References: <CAF_YUvVJnqehHZLR6pML=UA-n1j4oAmABciUhB4Ek9R+G+G7QA@mail.gmail.com><CH2PR04MB6950EEBF6DFE85F62D0B644EE0299@CH2PR04MB6950.namprd04.prod.outlook.com>
Sure -- mention of "software" is irrelevant here. Totally agree there.
But still pondering this...
On Mon, Oct 17, 2022 at 5:18 PM Bollinger, John C via coreDMG <[email protected]> wrote:
Hi Bob,
Yes, when a moiety is disordered about a symmetry element with multiplicity 2, such as a 2-fold rotation axis, there will be half as many per unit cell as there would ordinarily be for a moiety at a general position of the space group -- much the same as if it were ordered (and therefore symmetric) around the symmetry element. Analogous applies for disorder around higher-symmetry positions.
My thinking is that the crystallographer might recognize "a" special symmetry element, but the application of symmetry creates n copies, not two, in a space group with n symmetry operations. Right?
Thus, fundamentally, there is no such concept of a "specific" symmetry element. All n copies symmetry related, but all are not "complementary".
John, I appreciate the addition of "one or more" here. In the example I have, symmetry element 2 is a C2 axis parallel to the b axis in the ab plane that generates the overlapping pairs. Thus:
Symmetry operation 5 is a center of inversion at {0 0 0} that equally well describes the disorder, pairing them differently:
and symmetry element 7 is a center of inversion at {1/4, 1/4, 1/4}
This group can be considered to be disordered about any of these symmetry elements.
I'm not sure I understand this statement:
In addition to not being occupied simultaneously with sites belonging to
different groups, the sites of such a group also are not occupied
simultaneously
with symmetry equivalents of sites belonging to the same group. That
is, the group's symmetry equivalents are among its disorder complements.
I don't understand this statement. Why would it be true that sites related by symmetry are "not being occupied simultaneously"? If there are eight symmetry operations, four of those have to map to one disorder complement, and four have to map to the opposite. Pretty sure that has to be true, because we generated all eight from the same atoms. Don't half of those have to be occupied simultaneously?
True, only half of these can be occupied in any given unit cell, but I don't think we can know which of these four are occupied and which not in a given unit cell. Can we? -- Except for the obvious that if they have overlapping electron densities, then that's not possible.
To say it another way, I can pick any two Cl atoms in this unit cell and determine the space group operation relating them. Half of these, I guess, would be considered "complementary" but the others would be simultaneously occupied.
I think only half of the group's symmetry equivalents are among its disorder complements. At least in this case. Pretty sure that is not a general statement, either.
Bob
_______________________________________________ coreDMG mailing list [email protected] http://mailman.iucr.org/cgi-bin/mailman/listinfo/coredmg
[Send comment to list secretary]
[Reply to list (subscribers only)]
- Follow-Ups:
- RE: Ambiguity in atom_site.disorder_group value -1 (Bollinger, John C via coreDMG)
- References:
- Ambiguity in atom_site.disorder_group value -1 (Robert Hanson via coreDMG)
- Re: Ambiguity in atom_site.disorder_group value -1 (Bollinger, John C via coreDMG)
- Prev by Date: Re: Ambiguity in atom_site.disorder_group value -1
- Next by Date: RE: Ambiguity in atom_site.disorder_group value -1
- Prev by thread: Re: Ambiguity in atom_site.disorder_group value -1
- Next by thread: RE: Ambiguity in atom_site.disorder_group value -1
- Index(es):

