Acta Cryst. (1985). A41, 278-280

Nomenclature for crystal families, Bravais-lattice types and arithmetic classes

Report of the International Union of Crystallography Ad-Hoc Committee on the nomenclature of symmetry*

BY P. M. DE WOLFF (Chairman), Department of Applied Physics, Delft University of Technology, Lorentzweg 1, 2628 CJ Delft, The Netherlands

N. V. BELOV,⁺ Institute of Crystallography, Academy of Sciences of the USSR, Leninsky pr. 59, Moscow 117333, USSR

E. F. BERTAUT, Laboratoire de Cristallographie, CNRS Grenoble, 25 Avenue des Martyrs, BP 166X Centre de Tri, 38042 Grenoble CEDEX, France

M. J. BUERGER, PO Box 361, Lincoln Center, MA 01773, USA

J. D. H. DONNAY, Department of Geological Sciences, McGill University, 3450 University Street, Montreal, Canada H3A 2A7

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Philipps-Universität, Lahnberge, D-3350 Marburg (Lahn), Federal Republic of Germany

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5l00 Aachen, Federal Republic of Germany

V. A. KOPTSIK, Moscow State University, Department of Physics, Leninskiye Gory, Moscow 117234, USSR

A. L. MACKAY, Department of Crystallography, Birkbeck College, London Wi E 7HX, England

H. WONDRATSCHEK, Institut für Kristallographie, Universität, Kaiserstrasse 12, D-7500 Karlsruhe, Federal Republic of Germany

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemical Laboratory, Lensfield Road, Cambridge CB2 1EW, England

AND S. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), AT&T Bell Laboratories, Murray Hill, NJ 07974, USA

(Received 13 August 1984; accepted 13 November 1984)

Abstract

Standard symbols representing crystal families, two- and three-dimensional Bravais-lattice types and arithmetic classes are recommended for use by the IUCr. The six crystal families are designated by lower-case letters. The family letter in the symbol of each of the 14 lattice types is followed by an upper-case letter to distinguish different lattice types within the family. Arithmetic classes are indicated by modified symbols of the corresponding symmorphic space groups.

Crystal families

Six lower-case letters, which originate from words denoting the shape of commonly used unit cells, are recommended as the standard designation of crystal families (Table 1). A 'crystal family' is a well defined and unambiguous concept in crystallography [International Tables for Crystallography (1983), sections 2.1 and 8.2.6]. Comparing the classification into crystal families with existing classifications into 'crystal systems', it is noted that they coincide except for the hexagonal family in three dimensions, which contains all 'hexagonal', 'trigonal' and 'rhombohedral' space groups. Although this set is often regarded as a single 'crystal system' in the American and Russian literature, other widespread usage divides it into two different systems. Therefore, association of the lower-case letters with crystal systems (instead of families) is apt to cause confusion and is not recommended by the Ad-hoc Committee.

Adoption of these symbols yields a clear interpretation of the lattice symbols, see below. Direct applications are not envisaged but future use is likely, since the ambiguity of the term 'crystal system' (see above) has so far prevented the general acceptance of a suitable nomenclature for this scale of classification. No such difficulty exists with the term 'crystal families'.

---

Table 1. Standard symbols for the crystal families

            Two-dimensional    Three-dimensional
 Symbol      crystal family     crystal family


   a         -                  Triclinic (anorthic)
   m         Oblique            Monoclinic
   o         Rectangular        Orthorhombic
   t         Square             Tetragonal
   h         Hexagonal          Hexagonal
   c         -                  Cubic

---

Bravais-lattice types

Symbols for designating Bravais-lattice types independently of any description by a particular unit cell with labelled axes are presented in Table 2. The initial lower-case letter characterizes the crystal family (see above) to which the Bravais-lattice type belongs. The second letter designates the type of centring. These symbols are identical with those listed in International Tables for Crystallography (1983) and used in the 60-year index to Structure Reports (1976),⁺⁺ with the exception of mS and oS, which replace mC and oC.

The letter C in the monoclinic and orthorhombic Bravais-lattice-type symbols is ambiguous since C is closely associated with one of the common setting and/or unit-cell choices for the lattice, namely A, C or I centring for the monoclinic family and A, B or C centring for the orthorhombic family. The Ad-hoc Committee has chosen the latter S, derived from 'side-face centred' (i.e. seitenflächenzentriert), to replace C. This letter, which is also used to designate similarly centred four-dimensional lattices (Wondratschek, Bülow & Neubüser, 1971), is clearly appropriate for oS-type lattices. In the case of mS-type lattices, the letter S evokes neither an A- nor a C-centred in preference to an I- centred unit cell: the symbol for the monoclinic centred lattice remains mS regardless of the basis actually used.

A similar comment applies to the symbol hR, which designates the rhombohedral lattice regardless of whether that lattice is described (using rhombohedral coordinates) by a primitive rhombohedral unit cell or (using hexagonal coordinates) by a hexagonal unit cell.

---

Table 2. Standard symbols for the Bravais lattice types

          Two-dimensional         Three-dimensional
 Symbol    lattice type     Symbol  lattice type

   mp  Oblique               aP Triclinic
   op  Rectangular primitive mP Monoclinic primitive
   oc  Rectangular centred   mS Monoclinic centred
   tp  Square                oP Orthorhombic primitive
   hp  Hexagonal             oS Orthorhombic single-face
                                centred
                             oI Orthorhombic body-
                                centred
                             oF Orthorhombic all faces
                                centred
                             tP Tetragonal primitive
                             tI Tetragonal body-centred
                             hP Hexagonal primitive
                             hR Rhombohedral
                             cP Cubic primitive
                             cI Cubic body-centred
                             cF Cubic face-centred

---

Arithmetic classes

The Ad-hoc Committee recommends that an arithmetic class be designated by the modified symbol of the symmorphic space group contained in that class. The modification consists of interchanging the lattice letter and the point-group symbol. For example, instead of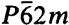 , write 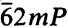for the arithmetic class.

An arithmetic class is a class of space groups. Two space groups belong to the same arithmetic class if the following procedure leads to identical results for both:

(a) In the Hermann-Mauguin symbol replace screw axes by rotation axes and glide planes by mirror planes.

(b) Write the ensuing symbol in standard form, e.g. Cmm2 for A2mm.

The result is the (standard) symbol of a symmorphic space group. It follows that the arithmetic class can be represented by the type of symmorphic space groups that it contains.

The arithmetic class is a concept widely used in symmetry classification and in mathematical crystallography. The proposed code not only characterizes the class adequately, but is also recognizable as a code for just this purpose.⁺⁺⁺

For further discussion of arithmetic classes, see International Tables for Crystallography (1983).

References

International Tables for Crystallography (1983). Vol. A, especially sections 2.1 and 8.2. Dordrecht: Reidel.

Laves, F. (1966). Report to Seventh General Assembly of IUCr, p. 27, Appendix D(a), Moscow.

Pearson, W. B. (1967). A Handbook of Lattice Spacings and Structures of Alloys, Vol. 2. New York:Pergamon Press.

Structure Reports (1976). 60-Year Structure Index 1913-1973. A. Metals and Inorganic Compounds. Utrecht: Bohn, Scheltema & Holkema.

Wondratschek, H., Bülow, R. & Neubüser, J. (1971). Acta Cryst. A27, 523-535.

---

* Appointed 18 March 1980 under ground rules outlined in Acta Cryst. (1979), A35, 1072. Final Report accepted 17 August 1984 by the IUCr Commission on Crystallographic Nomenclature and 13 November 1984 by the Executive Committee.
⁺ Deceased 6 March 1982.
⁺⁺ The first use of this nomenclature was in an example cited by Laves (1966) as chairman of the IUCr Subcommittee on Structure Type Designation. All 14 symbols were published and extensively used by Pearson (1967).
⁺⁺⁺ Note added in proof by the Chairman: The new symbol for classes with symmorphic group symbol Pm and Cm is identical (mP) or very similar (mC) to one of the new lattice type symbols given in the preceding section. In view of the context in which the symbols will be used, confusion is not expected to occur.