Acta Cryst. (1989) A45, 494-499

Definition of symmetry elements in space groups and point groups

Report of the International Union of Crystallography Ad-Hoc Committee on the nomenclature of symmetry*

By P. M. DE WOLFF (Chairman), Department of Applied Physics, Delft University of Technology, PO Box 5046, 2600 GA Delft, The Netherlands

Y. BILLIET, Ecole Nationale d'Ingénieurs, BPW 3038 Sfax, Tunesië

J. D. H. DONNAY, Department of Geological Sciences, McGill University, 3450 University Street, Montreal, Canada H3A 2A7

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Federal Republic of Germany

R. B. GALIULIN, Institute of Crystallography, Academy of Sciences of the USSR, Leninsky Prospekt 59, Moscow 117333, USSR

A. M. GLAZER, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU, England

MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, USA

D. P. SHOEMAKER, Chemistry Department, Oregon State University, Corvallis, OR 97331, USA

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Federal Republic of Germany

TH. HAHN (ex officio, IUCr President), Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Federal Republic of Germany

A. J. C. WILSON (ex officio, IUCr Commission on International Tables ), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England

and S. C. ABRAHAMS $\dagger$ (ex officio, IUCr Commission on Crystallographic Nomenclature), AT&T Bell Laboratories, 600 Mountain Avenue, Murray Hill, NJ 07974, USA

(Received 24 November 1988; accepted 15 March 1989 )

*Appointed 14 November 1984 and 10 August 1987 (see Acta Cryst. (1986). A42, 64 for original membership) under ground rules outlined in Acta Cryst. (1979). A35, 1072. Final Report accepted 10 January 1989 by the IUCr Commission on Crystallographic Nomenclature and 15 March 1989 by the IUCr Commission on Crystallographic Nomenclature and 15 March 1989 by the Executive Committee.

$\dagger$ Present address: Institut für Kristallographie der Universität Tübingen, Charlottenstrasse 33, D-7400 Tübingen, Federal Republic of Germany.

Abstract

A 'geometric element' is defined, for any given symmetry operation, as a geometric item that allows the operation (after removing any intrinsic translation) to be located and oriented. In the case of an inversion, a (screw-) rotation or a (glide-) reflection, it is respectively a point, line or plane. In the case of a rotoinversion, the geometric element consists of the axis of the rotation part and the center of the inversion part. As a general concept, the geometric element may be justified by a mathematical definition (as given in the Appendix). A 'symmetry element' (of a given crystal structure or object) is defined as a concept with a double meaning, namely the combination of a geometric element with the set of symmetry operations having this geometric element in common ('element set'). There is no overlap between element sets of a given structure. Together with the identity and the translations, for which a geometric element is not defined, the element sets cover all symmetry operations.

Introduction

The Ad-hoc Committee was set up in 1980 to 'consider nomenclature problems concerning symmetry operations and symmetry elements in space groups'. With regard to symmetry operations, the only problem is that of the appropriate symbols; however, a complete notation has been adopted in International Tables for Crystallography (1983) (referred to hereafter as IT A83).

The term 'symmetry element' is widely used only by crystallographers, mineralogists and spectroscopists. It is the collective designation for a number of concepts which - judging from their names - appear to be of a geometric nature: a rotation axis, a mirror plane etc. An essential feature of symmetry elements is the connection between such geometric items and one or more symmetry operations of a given space group or point group. This connection has consisted in the past of a traditional set of ad-hoc assignments of geometric items to symmetry operations. It has been the foremost goal of our Ad-hoc Committee to put that set on the footing of a precise and unified general definition.

In the successive editions of the International Tables for Crystallography, only IT A83 and later editions contain an explicit description of symmetry elements; see its Table 1.3. The last column of that table is headed: 'Generating symmetry operation with glide or screw vector'. The term 'generating' is not explained; it is taken to mean that if a structure has a symmetry operation listed here, then the corresponding 'symmetry element' listed in the second column, with its symbol as in the first, is present. However, that interpretation leads to several problems:

(1) The table reflects the usual ad-hoc assignment; again there is no clue to a unified definition.

(2) The geometric item is obvious for a (glide-) reflection, a (screw-) rotation and an inversion. For a rotoinversion, however, the term 'rotoinversion axis' in column 2 is unclear. It suggests a mere line, but that is not sufficient to determine the operation.

(3) According to this table, a plane such as xy0 in space group Cmma (67), for instance, is both an a- and a b-glide plane. The current symbol 'a' is awkwardly biased. More serious is the resulting apparent ambiguity of the concept 'glide plane'.

(4) In Cmmm (65), two possible 'generating' symmetry operations share a plane. One is the reflection (x, y, -z), the other is an n-glide reflection ( $\frac{1}{2} + x, \frac{1}{2} + y, -z$ ). The table identifies the plane xy0 as a mirror plane as well as an n-glide plane, and the current symbol 'm' may hence seem inappropriate. Again the question arises: what is 'a glide plane'? And what if it can also be a mirror plane?

(5) There are also glide planes for which there is no conventional symbol in IT A83. Corresponding glide reflections are labelled 'g' in IT A83. They occur, for example, in space groups P4bm (100), P4/nbm (125), P4₂/nnm (134), R3m (160) and $Fm\bar{3}m$ (225).

Problem 1, in particular the uncertain meaning of 'a glide plane', formed a major difficulty for the Ad-hoc Committee when it attempted to design an improved nomenclature for symmetry elements. We therefore undertook the formation of an unambiguous definition of 'symmetry element'. Since this term is sometimes confused with 'group element', adoption of a new name without the word 'element' was contemplated. The original term was nevertheless finally retained since it is so firmly rooted in the crystallographic literature.

The Ad-hoc Committee, however, has introduced the auxiliary new concepts 'geometric element' and 'element set', in the expectation that they will allow use of the term 'symmetry element' in the sense precisely specified below, which does not seriously conflict with the previous use of the term. In $\S$ 5 we reexamine the above problems 2 to 5 in the light of the new definition.

1. Geometric elements

Each symmetry operation of a point group or space group belongs to one of the eight categories in Table 1, column 1. In order to describe these operations, a geometric element (Table 1, column 2) may be assigned to each but the first two. The geometric element is defined as a geometric item that allows the reduced symmetry operation in space to be located and oriented. It does not contain numerical parameters such as a rotation angle or the components of the glide vector of glide reflections (last column). It may, however, be defined much less ambiguously so as to yield almost exactly the entries in the second column, cf. Appendix.

**Table 1:** *Geometric elements of symmetry operations in point groups and space groups*
Symmetry operation	Geometric element	Additional parameters
Identity	Not required	None
Translation	Not required	Vector t
Reflection in plane A	Plane A	None
Glide reflection = reflection in plane A and translation v parallel to A	Plane A	Glide vector v
Rotation about line b	Line b	Angle and sense of rotation
Screw rotation = rotation about line b and translation u parallel to b	Line b	Angle and sense of rotation, screw vector u
Rotoinversion = rotation about line b and inversion through point P on b	Line b and point P on b	Angle (not equal to $\pi$ ) and sense of rotation
Inversion through point P	Point P	None

2. Symmetry elements

Two or more different symmetry operations of the same space group or crystal structure may have identical geometric elements, even when they belong to different categories as specified by Table 1. An example is provided by the powers of a rotation (same category) or by a reflection and a glide reflection in the same plane (different categories). In a given space group, the complete set of symmetry operations which have the same point or line etc. as their common geometric element will be called the element set of that geometric element.

The combination of a geometric element and its element set is indicated by the term 'symmetry element' (Table 2). This allows such statements as 'This point lies on a rotation axis', and also 'The operations belonging to a glide plane' to be made.

**Table 2:** *Symmetry elements in point groups and space groups*
Name of symmetry element	Symbol	Geometric element	Defining operation (d.o.)	Operations in element set
Mirror plane	Em	Plane A	Reflection in A	D.o. and its coplanar equivalents*
Glide plane	Eg	Plane A	Glide reflection in A, $2\nu$ (not $\nu$ ) a lattice translation	D.o. and its coplanar equivalents*
Rotation axis	En	Line b	Rotation about b, angle $2{\pi}/n,n=2,3,4$ or 6	1st $\dots(n-1)$ th powers of d.o., and their coaxial equivalents $\dagger$
Screw axis	En_j	Line b	Screw rotation about b, angle $2{\pi}/n,u=j/n$ times shortest lattice translation along b, right-hand screw; n= 2,3,4 or 6, $j=1,\dots,(n-1)$	1st, $\dots,(n-1)$ th powers of d.o., and their coaxial equivalents $\dagger$
Rotoinversion axis	$E\bar{n}$	Line b and point P on b	Rotoinversion: rotation about b, angle $2{\pi}/n$ , and inversion through P; n=3, 4 or 6	D.o. and its inverse
Center	$E\bar{1}$	Point P	Inversion through P	D.o. only

*That is, all glide reflections with the same reflection plane, with glide vectors differing from that of d.o. (taken to be zero for a reflection) by a lattice translation vector.

$\dagger$ That is, all rotations and screw rotations with the same axis, b, the same angle and sense of rotation, and the same screw vector u (zero for a rotation) up to a lattice translation vector.

The first column of Table 2 lists the name of the symmetry element. Of the four different kinds of geometric elements (Table 1), 'point' and 'point plus line' each yield one type of symmetry element. Two types arise from both 'plane' and 'line', depending on the presence or absence of a pure reflection and a pure rotation in the element set (cf. $\S$ 5). The symbols in the second column all begin with E, thereby indicating symmetry elements as defined in this Report.

The fourth column, 'defining operation', states what to look for in order to identify a symmetry element, for instance in a structure model. The defining operation alone (for which the simplest is selected when there is a choice) suffices. However, for a rotoinversion axis $E\bar{3}$ or $E\bar{6}$ , it will be easier to verify the presence of both its square and its cube, cf. $\S$ 3. The last column explicitly describes the full element set.

3. Partial symmetry elements

Element sets of fourfold and sixfold rotation and screw rotation axes have subsets which fully satisfy the specifications in Table 2, last column. However, they do not contain all symmetry operations with the given axis as geometric element. In order to distinguish such incomplete symmetry elements from the regular ones, it is recommended that they be referred to as 'partial symmetry elements'; they will be designated by EP instead of E. Examples: EP2 in E4; EP2₁ and EP3 in E6₃; EP2 and EP3₂ in E6₂.

The partial elements should not be confused with the regular symmetry elements defined by the powers of a rotoinversion: the square and cube of $\bar{6}^1$ (defining an E3 and an Em) and of $\bar{3}^1$ (defining an E3 and an $E\bar{1}$ ), and the square $\bar{4}^2$ which defines an E2. The symmetry elements so defined are regular and by no means partial, provided that the corresponding element set is not a subset of any other element set (as happens for $\bar{4}^2$ in the second example below).

4. Some examples

According to the above definition, each symmetry operation belongs to one and only one symmetry element (not counting partial elements). The latter is determined by the geometric element of the operation. For example, we can 'decompose' any site symmetry group into symmetry elements.

Example 1. A site symmetry with point group $\bar{6}$ consists of:
$\bar{6}^1$ and $\bar{6}^5$ ,	forming a rotoinversion axis $E\bar{6}$
$\bar{6}^2$ and $\bar{6}^4$ ,	belonging to a rotation axis E3
$\bar{6}^3$ ,	belonging to a mirror plane Em.

This 'decomposition' is always exhaustive (the identity operation is not listed in these examples since it occurs in every point group). Strictly speaking, it is not a true decomposition, because the mirror plane for instance has in its element set not only the reflection but also the infinite number of coplanar equivalents which are of course not part of the site symmetry.

Example 2. Site symmetry 4/m consists of:
4¹, 4² and 4³,	belonging to a rotation axis E4
$\bar{4}^1$ and $\bar{4}^3$ ,	forming a rotoinversion axis $E\bar{4}$
m¹,	belonging to a mirror plane Em
$\bar{1}^1$ ,	forming a center $E\bar{1}$ .

Example 3. Site symmetry 2/ $m\, \bar{3}$ consists of:
$4 \times (3^1$ and 3²),	belonging to four rotation axes E3
$4 \times (\bar{3}^1$ and $\bar{3}^5$ ),	forming four rotoinversion axes $E\bar{3}$
$3 \times 2^1$ ,	belonging to three rotation axes E2
$3 \times m^1$ ,	belonging to three mirror planes Em
$\bar{1}^1$ ,	forming a center $E\bar{1}$ .

5. Comparison with IT A83

The essential feature of the definition of symmetry elements in Table 1.3 of IT A83 is that they are defined by a 'generating symmetry operation'. In mathematics, an operation 'generates' a certain group which is clearly not meant here. Hence, 'generating' is taken as having the sense of 'characteristic for'. Thus, Table 1.3 leads to the ambiguous or uncertain problems 2 to 5 of the Introduction.

By contrast, the concept 'symmetry element' in the present proposal depends primarily not on a single operation but on a geometric element (GE). Given that GE, it is the element set (consisting of the operations sharing that GE) that determines the nature of (and, eventually, the symbol for) the symmetry element. There is always just one such set, so that no ambiguity can exist and it is only the symbol which may be open to discussion.

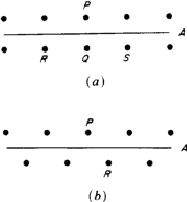
Since the difficulties with the IT A83 description occur mainly with glide planes, these are now re-examined. In Fig. 1(a) we may imagine that, for a given crystal structure, $P \rightarrow Q$ represents a symmetry reflection through the plane A.

It may be recalled that there also exists an infinite number of glide reflections (all of them symmetry operations) with respect to the same plane: $P \rightarrow R, S$ etc. (These are the coplanar equivalents of the operation $P \rightarrow Q$ mentioned in Table 2.) All these operations have the plane A as their common GE; together with the reflection they form the element set. In the present definition, the symmetry element in this case is always a mirror plane. In particular, problem 4 of the Introduction falls in this category. The new definition does not allow the xy0 plane in space group Cmmm to be called 'a mirror and also an n-glide plane'. The fact that one of the coplanar equivalents happens to have the shift (a + b)/2, which is a lattice translation, does not change the nature (mirror plane) of the symmetry element.

The other alternative occurs if a glide reflection $P \rightarrow R$ is given through plane A, and none of its coplanar equivalents [discussed in note (iv) to Table 1.3 in IT A83] is a reflection (Fig. 1b). Then, plane A is always a glide plane. The present Report recognizes only geometrically distinct symmetry elements. Hence, in the case of problem 3 of the Introduction, an interpretation such as 'both an a- and a b-glide plane' should no longer be possible: here the plane xy0 is just one single glide plane, whatever symbol is assigned to it. It is recommended that the symbols used to express this primary differentiation between mirror and glide planes. This can be done simply by reserving 'm' exclusively for mirror planes, as was done by calling them Em. Any differentiation between various kinds of glide planes falls beyond the scope of the present Report.

The 'special' glide planes of problem 5 in the Introduction need no further discussion beyond the statement that they are true glide planes, without special distinction in the sense of this Report.

A very similar situation exists for twofold axes. If, for a given twofold axis, a 180 $^{\circ}$ screw rotation $P \rightarrow R$ is a symmetry operation, then combination with all symmetry translations parallel to the axis generates the element set consisting of infinitely many operations. If, among these, there is a rotation of 180 $^{\circ}$ such as $P \rightarrow Q$ in Fig. 1(a) (where A now represents the axis), then the symmetry element is a twofold rotation axis E2. If there is no such operation among them (Fig. 1b), then the symmetry element is a two-fold screw axis E2₁. An axis cannot be both simultaneously, as a strict application of Table 1.3 in IT A83 would require for twofold axes parallel to (110) in structures with cF lattices; such axes can only be rotation axes.

Problem 2 of the Introduction has been solved in this Report by taking the conventional 'line-plus-point' GE for a rotoinversion.

**Figure 1:** (a) Array related by the mirror plane A. (b) Array related by the glide plane A.
$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

APPENDIX

General definition of geometric elements

A1. Introduction

The assignment in Table 1 of geometric elements to symmetry operations has been performed in such a way that symmetry elements are in accordance with crystallographic tradition. The difference from that tradition is, firstly, that the two-sided character of symmetry elements has been made explicit and unambiguous through the introduction of geometric elements and element sets. The second difference, in the present definition, is that the geometric item is defined primarily for each single operation whereas existing definitions of 'symmetry element' tend to be associated with a (cyclic?) group of operations. For instance: 'The geometrical locus about which a group of repeating operations act is called a symmetry element' (Buerger, 1963); or 'It is imperative to distinguish between symmetry operations (group elements) and symmetry elements (cyclic groups)' (Donnay $\&$ Donnay, 1972).

The Ad-hoc Committee had previously discussed proposals to establish such a group assignment, but had found them awkward when applied to space groups in which non-cyclic site symmetries occur. Existing definitions, such as the two just cited, do not specify exactly which group belongs to a given geometric item. Therefore, it was decided to drop the group association and first define the 'geometric element' for each given operation.

The obvious aim of such a definition is to provide a 'space anchor' for the orientation and the location of the operation. With that aim in view, there is actually little choice. For point-group operations only the orientation is needed, whereupon the real eigenvector(s) of the operation yield the geometric elements of Table 1 almost uniquely (not quite uniquely: the eigenvector with negative eigenvalue of the reflection, for instance, can be omitted but that of a rotoinversion cannot). Extension to space-group elements, fixing their location as well, is also easy but not entirely automatic.

The question hence arises whether a general definition can be given for space groups as well. The purpose of this Appendix is to review some of the past attempts in that direction, and to present a new interpretation ( $\S A$ 3). The latter produces Table 1 directly.

A2. Previous efforts

In the past, a symmetry element has sometimes been described as a line, plane or point which is invariant for (that is, not displaced by) a symmetry operation. Stated in that form, such a description is useless. For example, a reflection leaves not only the mirror plane in place, but also all planes perpendicular to it, which are clearly not wanted. Hence the line etc. must not only be invariant as a whole, but every point on it must remain in place. A definition of the geometric element for a given symmetry operation may thus be 'the subspace consisting of invariant points' ('SCIP'). An obvious difficulty then arises in dealing with operations such as screw rotations and glide reflections, for which no point whatever is invariant. The solution for this problem is to remove from the given operation its 'intrinsic translation', the latter being parallel to an invariant direction of the operation. The reduced operation thereby results, with a fully determined position for the reflection plane, or the axis of rotation, which now becomes the geometric element.

This term also applies to operations that have zero intrinsic translation: a (roto-) inversion or a pure reflection or rotation. For these, the given operation is identical to its reduced operation. The other extreme occurs when the given operation is a mere translation. In that case the reduced operation is just the identity. The geometric element of any given operation is hence defined as the 'subspace consisting of all invariant points for the reduced operation' ('SCIPRO').

The SCIPRO definition of geometric elements apparently yields the results given in Table 1, but a severe discrepancy remains for the category of rotoinversions for which it yields just one point. In Table 1, the traditional axis line has been added because otherwise the rotoinversion would not be oriented. In all other categories, the reduced operation is completely located as well as oriented by the geometric element as defined by SCIPRO. However, the fact that SCIPRO fails for rotoinversions shows that the 'invariant-points' reasoning, which led to the SCIPRO definition, is basically inadequate.

A3. A new interpretation

A new interpretation of the geometric element assigned to a given symmetry opration W by Table 1 follows:

Consider the Euclidean normalizer of W, that is, the group of all congruence operations which 'commute with W'; in other words, which transform W into itself. The ten different types of normalizer for all possible operations W are listed in Table 3 (two types each for rotations and screw rotations as shown in the footnote to Table 3, and one type for each of the remaining six kinds of operation). All groups are noncrystallographic and continuous. In the case of a reflection in a plane, for example, the normalizer contains all parallel translations, reflections in all perpendicular planes, etc. The short and rather obvious description in the second column of Table 3 is, however, sufficient to yield the invariant subspaces listed in the third column. This latter column is in accordance with the second column of Table 1. The ensuing definition hence becomes: the geometric element of a symmetry operation W consists of the subspace(s) invariant for all operations belonging to the Euclidean normalizer of W.

**Table 3:** *Euclidean normalizers of symmetry operations and their invariant subspaces*
Symmetry operation W	Euclidean normalizer N of W consists of	Invariant subspace(s) of N
Identity	All congruences	None
Translation, vector t	Those congruences which conserve vector t	None
Reflection in plane A	Those congruences which conserve plane A	Plane A
Glide reflection in plane A, glide vector v	those congruences which conserve plane A and vector v	Plane A
Rotation about line b	Those congruences which conserve line b*	Line b
Screw rotation about line b, screw vector u	Those congruences which conserve line b and vector u*	Line b
Rotoinversion with respect to line b and point P	Those congruences which conserve line b and point P, as well as the sense of rotation	Line b, point P, and plane perpendicular to b through P
Inversion	Those congruences which conserve point P	Point P

*If the rotation angle is not 180 $^{\circ}$ , then the sense of rotation must also be conserved. The normalizer then lacks mirror planes through b, for instance. However this does not change its invariant subspaces.

The following remarks apply to Table 3:

(i) The occurrence of three items for the rotoinversion (instead of two in Table 1) is not a discrepancy: if the point is invariant, invariance of the line follows from that of the plane, and vice versa. Hence, one of the latter two is redundant.

(ii) 'Subspace' should be taken in the proper sense, because in the improper sense ('all space') it is invariant for any congruence. It would have to be added to all geometric elements but would not increase their information content.

(iii) The invariance need only obtain for the subspace as a whole, not necessarily pointwise as required in the SCIPRO definition.

(iv) It should be noted that the congruence operations referred to above are operations in point space (see IT A83, $\S$ 8.1.5), not vector space. The given definition of geometric elements hence applies to symmetry operations in point space only, not to those in vector space.

References

Buerger, M. J. (1963). Elementary Crystallography. New York: Wiley.

Donnay, J. D. H. & Donnay, G. (1972). Acta Cryst. A28, S110.

International Tables for Crystallography (1983). Vol. A, edited by TH. HAHN. Dordrecht: Reidel. (Present distributor Kluwer Academic Publishers, Dordrecht.)

International Tables for Crystallography (1987). Vol. A, Second, Revised Edition, edited by TH. HAHN, Ch. 15. Dordrecht: Reidel. (Present distributor Kluwer Academic Publishers, Dordrecht.)

Ledermann, W. (1973). Introduction to Group Theory. Edinburgh: Oliver and Boyd.


...reduced: The reduced operation is derived from a given operation by removing any intrinsic screw or glide translation. Hence, if the latter is zero, reduction does not change the operation.
...normalizer: The term 'Euclidean normalizer' is generally used in relation to subgroups of the group E of all congruences ('Euclidean mappings'), cf. International Tables for Crystallography (1987). In the sense used here (relating not to a subgroup but to a single group element W), the normalizer is also called the centralizer of W, cf. Ledermann (1973).

These pages are maintained by the Commission Last updated: 15 Oct 2021