Acta Cryst. (1992). A48, 727-732

Symbols for symmetry elements and symmetry operations

Final report of the International Union of Crystallography Ad-Hoc Committee on the nomenclature of symmetry*

By P. M. DE WOLFF (Chairman), Meermanstraat 126, 2614 AM Delft, The Netherlands,

Y. BILLIET, Ecole Nationale d'Ingénieurs, BPW 3038 Sfax, Tunesië,

J. D. H. DONNAY, Department of Geological Sciences, McGill University, 3450 University Street, Montreal, Canada H3A 2A7,

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Germany,

R. B. GALIULIN, Institute of Crystallography, Academy of Sciences of Russia, Leninsky Prospekt 59, Moscow 117333, Russia,

A. M. GLAZER, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU England,

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Germany,

MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, USA,

D. P. SHOEMAKER, Chemistry Department, Oregon State University, OR 97331, USA,

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Germany,

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England

AND S. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA

(Received 7 November 1991; accepted 9 March 1992)

* Appointed 14 November 1984, modified 10 August 1987 [see Acta Cryst. (1986), A42, 64 for original membership] under ground rules outlined in Acta Cryst. (1979), A35, 1072. Final Report accepted 23 December 1991 by the IUCr Commission on Crystallographic Nomenclature and 9 March 1992 by the Executive Committee.

Abstract

New or redefined printed symbols are proposed in the light of the recently accepted redefinition of symmetry elements [de Wolff et al. (1989). Acta Cryst. A45, 494-499]. In particular, the letter e covers certain glide planes which hitherto had no unique symbol, such as those called 'either a or b'. The use of e in the Hermann-Mauguin symbol of five different space groups is recommended. For e planes projected in a direction parallel to the plane, a graphical symbol is proposed which removes the ambiguity of their present designation. The letter k is proposed for a newly defined class of glide planes which until now were without specific symbol. The symbols for symmetry operations introduced in the space-group descriptions of International Tables for Crystallography (1989), Vol. A (Dordrecht: Kluwer Academic Publishers) are recommended for general use, with modifications only for glide reflection operations.

Introduction

The Ad-hoc Committee appointed in 1980 to consider 'nomenclature problems concerning symmetry operations and symmetry elements in space groups' has issued two Reports entitled Nomenclature for Crystal Families, Bravais-Lattice Types and Arithmetic Classes (de Wolff et al., 1985) and Definition of Symmetry Elements in Space Groups and Point Groups (de Wolff et al., 1989). As noted in the 1989 Report, the only outstanding problem concerning symmetry operations is that of choosing appropriate symbols, since the concept is clear. A provisional notation has been adopted in International Tables for Crystallography (1983, 1989), referred to hereafter as ITA83.

1. Printed symbols for symmetry elements

The definition of symmetry elements as given in the 1989 Report (de Wolff et al.) will be used throughout the present Report. Here we repeat the essence:

For any given symmetry operation its geometric element (plane, point and/or line) is defined. A symmetry element is the combination of the geometric element of one of the symmetry operations in a given space group with the set (called `element set') of all symmetry operations in that space group which share this geometric element.

Explicit definitions of geometric elements and descriptions of the ensuing symmetry elements as well as their symbols are given in Tables 1 and 2. (These are identical to Tables 1 and 2 in the 1989 Report except for glide planes and are repeated here for completeness, see below). Each symmetry element is represented by a symbol consisting of two characters. The first character is an upper-case E for all symmetry elements. It serves to show that the symbol refers to a symmetry element and not, for instance, to a symmetry operation. If this is clear already from the context, then the E may be omitted, e.g. 'an axis 2' instead of 'an axis E2'.

**Table 1.** Geometric elements of symmetry operations in point groups and space groups
Symmetry operation	Geometric element	Additional parameters
Identity	Not required	None
Translation	Not required	Vector $\mathbf{t}$
Reflection in plane A	Plane A	None
Glide reflection =reflection in plane A and translation $\mathbf{v}$ parallel to A	Plane A	Glide vector $\mathbf{v}$
Rotation about line b	Line b	Angle and sense of rotation
Screw rotation = rotation about line b and translation $\mathbf{u}$ parallel to b	Line b	Angle and sense of rotation screw vector $\mathbf{u}$
Rotoinversion = rotation about line b and inversion through point P on b	Line b and point P on b	Angle (not equal to $\pi$ ) and sense of rotation
Inversion through point P	Point P	None

The symbol Eg listed in the 1989 Report can be used for glide planes if one merely wants to show that the symmetry element is a glide plane. On the other hand, if it belongs to one of the special kinds which have long been denoted by an appropriate letter (a, b, c, n or d; cf. ITA83), then that letter replaces g in Eg.

**Table 2.** Symmetry elements in point groups and space groups
Name of symmetry element	Symbol	Geometric element	Defining operation (d.o.)	Operations in element set
Mirror plane	Em	Plane A	Reflection in A	D.o. and its coplanar equivalents*
Glide plane	Eg $\ddag$	Plane A	Glide reflection in A, 2v (not v) a lattice translation	D.o. and its coplanar equivalents*
Rotation axis	En	Line b	Rotation about b, angle $2\pi/n$ ,n = 2, 3, 4 or 6	1st, $\dots$ ,(n - 1)th powers of d.o. and their coaxial equivalents $\dag$
Screw axis	En_j	Line b	Screw rotation about b, angle $2\pi/n$ , u =j/n times shortest lattice translation along b, right-hand screw; n = 2, 3, 4 or 6, $j=1,\dots,(n-1)$	1st, $\dots$ ,(n - 1)th powers of d.o. and their coaxial equivalents $\dag$
Rotoinversion axis	$E\bar n$	Line b and point P on b	Rotoinversion: rotation about b, angle $2\pi/n$ , and inversion through P; n = 3, 4 or 6	D.o. and its inverse
Center	$E\bar 1$	Point P	Inversion through P	D.o. only

* That is, all glide reflections with the same reflection plane, with glide vectors differing from that of the d.o. (taken to be zero for a reflection) by a lattice translation vector.
$\dag$ That is, all rotations and screw rotations with the same axis b, the same angle and sense of rotation and the same screw vector $\mathbf{u}$ (zero for a rotation) up to a lattice translation vector.
$\ddag$ In Eg, g is replaced by a, b, c, n, d, e or k for specific kinds of glide planes, cf. §2.

An important new aspect of symbols like Eb may, however, be pointed out. According to ITA83, denoting a plane by b merely meant that a glide reflection in the plane with a glide component b/2 along the b axis is a symmetry operation. This definition certainly applies to the situation depicted in Fig. 1.

**Fig. 1.** (After W. Fischer.) The element set of an Eb-glide plane, shown as a set of points above (+) and below (-) the plane produced by glide reflections in the plane, starting for instance from the + sign at upper left. The net N of translations parallel to the plane (+ $\cdots$ + vectors) is indicated by a mesh, which in this case happens to be rectangular. Both pairs of edges are parallel to crystal axes. There is a glide reflection with its glide vector (+ $\cdots$ -) along the b axis.
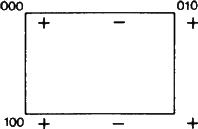$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

Fig. 1 is adapted, as are Figs. 2 and 3, from a set of similar figures designed by Ad-hoc Committee member W. Fischer as an inventory of all types of glide plane. Although the set was presented to the Committee in 1980, long before the 1989 Report came out, each of its figures shows precisely the 'element set' of the glide plane as defined in that Report (cf. the above summary). For a glide plane, the element set consists of all glide reflections having the plane as their common geometric element. Their action is shown in projection upon this plane. From the starting position of any + sign, each - sign results from one of the glide reflections of the set. All of these are shown within an elementary mesh of the resulting two-dimensional periodic pattern of + and - signs.

We shall often refer to the net N formed by all translations parallel to the plane; this net is easily visualized by looking at + signs only. These vectors are to be distinguished sharply from the vectors connecting a + sign with any - sign, each of which is the glide vector of a glide reflection belonging to the element set.

The new aspect arises because, in some cases, by the ITA83 definition, the b-glide plane is also an a-glide plane; see Fig. 2. Clearly this happens only if the net N is orthogonal centred, because then the a glide can be changed into a b glide (and vice versa) by adding a centring translation. The practice so far has been to call such a glide plane arbitrarily either a or b, thus causing an unjustified bias and a lack of uniqueness in these symbols. Therefore, we propose that the case of Fig. 2 be covered by a separate symbol.

**Fig. 2.** (After W. Fischer.) The element set of an Ee-glide plane. *Cf.* caption of Fig. 1. Note that the net N here is orthogonal centred.
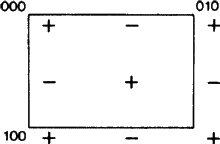$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

The scope of this symbol should then be extended to glide planes in a diagonal orientation, that is, parallel to just one crystal axis, provided that the glide plane has a glide vector along that axis and that the net N is orthogonal centred. For such planes there is not the ambiguity of the above a-b random choice, but the extended scope of the new symbol is in line with that of all existing symbols (namely a, b, c, n and d). Each of these is used for a glide plane with both one and two crystal axes in the net N, cf. Fig. 3.

The letter e is proposed for the new symbol. Thus, Ee will apply to glide planes with orthogonal centred nets N and at least one glide vector along a crystal axis. A new criterion is hence necessary: namely the orientation of glide vectors with respect to the conventional axes of the crystal. Since the latter are along symmetry directions, whereas every glide plane is parallel to a mirror plane of the lattice, it is not surprising that there is always at least one conventional crystal axis in N. If there is only one such axis, then perpendicular to it there is always another translation in N.

The new symbol e as well as old symbols a, b, c, d, n will now be redefined in terms of this new criterion and of the Bravais type of net N. This net is monoclinic or orthogonal or tetragonal primitive (mp or op or tp) or orthogonal centred (oc). [The Bravais-net-type symbols are those introduced in the Ad-hoc Committee's first Report (de Wolff et al., 1985).] Only oc-type nets N allow an Ee-glide plane. The symbol En is applicable to nets N of the Bravais type mp or op, whereas Ed is for oc-type nets N. (As stated in a footnote to Table 1.3 in ITA83: 'Glide planes d occur only in orthorhombic F space groups, in tetragonal I space groups, and in cubic I and F space groups. They always occur in pairs with alternating glide vectors'.) In contrast to Ea, Eb, Ec and Ee planes, however, for En and Ed planes there is no glide vector either parallel or perpendicular to a conventional axis in N.

The ensuing definitions of the glide planes of the above kinds are summarized in lines (i) and (ii) of Table 3, and more explicitly in Fig. 3.

**Table 3.** Printed symbols for special kinds of glide planes
Number of glide vectors parallel or perpendicular to crystal axes in net N	Bravais type of net N
The symbol is determined by two criteria. One criterion is the Bravais type (mp, op, tp or oc) of the net N formed by the symmetry translations parallel to the plane under consideration. This net always contains at least one conventional crystal axis.* The other criterion refers to the orientation of glide vectors with respect to such axes.
	m, op, tp	oc
(i) One or two parallel	Ec(Ea, Eb)	Ee
(ii) None parallel, none perpendicular	En	Ed
(iii) None parallel, one perpendicular	Ek	-

* As defined in ITA83, § 9.1; however, for rhombohedral space groups, hexagonal axes only are used here.

All remaining glide planes were previously without specific symbol. They each have a diagonal orientation (just one conventional crystal axis in the net N). Among the glide reflections in their element set, there is none with a glide vector along that axis. However, one glide vector is (by symmetry) perpendicular to it. A symbol seems desirable, so again a new letter is proposed: k. The new symbol Ek is briefly defined in line (iii) of Table 3 and is fully illustrated in the lower block of Fig. 3. Some examples are given in §2.

**Fig. 3.** (Adapted from W. Fisher's drawings.) All possible aspects of the element sets of glide planes shown as in Fig. 1, but independent of axis labels. The diagrams are grouped in columns headed by the Bravais-net-type symbol (top line) of their nets N, *cf.* Table 3. The other criteria of that table are verified by looking first at the double lines showing the directions of crystal axes in the plane. One edge (vertical) of the mesh of N shown is always chosen along such an axis. The other edge is horizontal except in (1) and (8). For diagrams (1), $\dots$ ,(5), the glide-plane symbol is the label a, b or c of the vertical axis; for the others it is the encircled letter in the outlined block containing the diagram. Note the vertical glide vectors in diagrams (1), $\dots$ ,(7), the horizontal ones in (6), (7), (14), (15) and the absence of either in (8), $\dots$ ,(13). An example of occurrence is given below each diagram by the space-group symbol and the coordinate triplet of the plane.
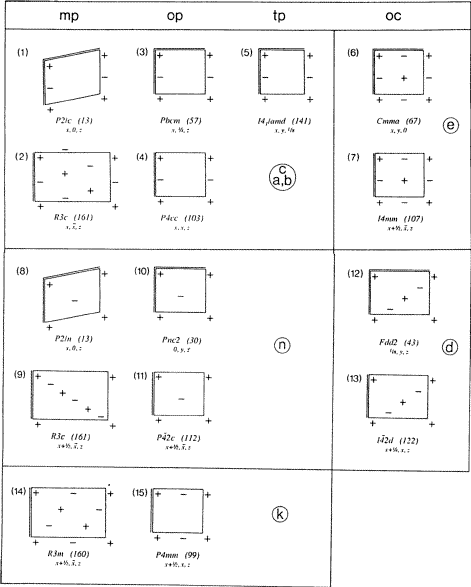$\begin{figure} \includegraphics {fig3.ps} \end{figure}$

In Fig. 3, Fischer's inventory of all types of glide plane is shown in an abbreviated - though still complete - fashion in which more graphical prominence has been given to the crystal axes. For each diagram, one example of its occurrence in a space group is listed.

In some rhombohedral space groups, diagonally oriented Ec, En and Ek planes occur with mp-type nets N which can be described by threefold centring of an orthogonal net. A rectangular triple mesh of the net N is shown for these types of glide planes in Fig. 3, diagrams (2), (9) and (14). In diagram (9), the similarity to other n diagrams such as (8) or (10) is recognized if in (9) a monoclinic primitive mesh of net N is considered with diagonal glide vectors.

2. Graphical symbols for symmetry elements

The existing graphical symbols as defined and used in ITA83 are considered to be adequate by the Ad-hoc Committee with one exception. The situation is very different from that of printed symbols because in drawings the projection direction becomes an added parameter. In the terms `perpendicular projection' and `parallel projection' used below, perpendicular and parallel refer to the orientation of the projection direction with respect to the glide plane.

For an Ee plane the symbol exists for its perpendicular projection. The existing graphical symbols for the parallel projection of an Ee-glide plane, however, suffer from the same ambiguity as the printed symbols. They express the glide vector either parallel or perpendicular to the projection direction, but the choice is arbitrary. Therefore, a new symbol is proposed for the parallel projection of an Ee glide plane, namely

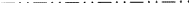
Examples of Ee planes.

All glide planes parallel to two axes in space groups Fmm2, Fmmm, $Fm\bar 3$ , $Fm\bar 3m$ and $Fm\bar 3c$ (Nos. 42, 69, 202, 225 and 226), as well as certain planes in the five space groups listed in §3.

Diagonally oriented Ee planes occur in space groups I4mm, I4cm, $I\bar 42m$ , I4/mmm, I4/mcm, $I\bar 43m$ and $Im\bar 3m$ (Nos. 107, 108, 121, 139, 140, 217 and 229).

In ITA83 all these Ee planes are drawn rather arbitrarily as either dotted or dashed lines in their parallel projections. Fig. 4 shows the diagram of space group I4cm (No. 108), both as shown in ITA83 and with use of the new symbol.

**Fig. 4.** (a) Diagram of space group I4cm (No. 108) taken from *ITA*83. (b) Same, modified by using the graphical symbol proposed in § 2, for the parallel projection of an Ee plane.
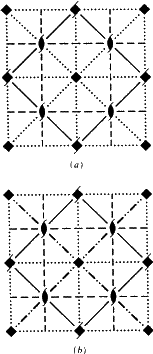$\begin{figure} \includegraphics {fig4.ps} \end{figure}$

Although Ek is a new print symbol, in the diagrams of ITA83 all glide planes Ek have been drawn satisfactorily with the same conventions as used for Ea/b/c glide planes. As in these cases, there is a single special glide vector (perpendicular to the crystal axis in net N, cf. Table 3). When this vector is, for instance, parallel to the plane of projection, the Ek plane is always drawn as the dashed line prescribed by the relevant convention. Therefore, no new graphical symbol is proposed for Ek glide planes.

Examples of Ek planes.

Such planes are readily found in the diagrams of ITA83 as planes parallel to just one axis and projected as dashed lines, e.g. xxz in P4bm and $P\bar 42_1m$ (Nos. 100 and 113). In particular, Table 3 is exactly in conformity with the distinction shown between Ek and En planes. See, for instance, the dashed and dot-dashed lines for R3m and R3c (Nos. 160 and 161).

3. Hermann-Mauguin space-group symbols

The characters appearing after the lattice letter in the Hermann-Mauguin (HM) symbol of a space group were originally meant to represent generating operations of the group. For instance, b was a b-glide reflection in a plane oriented according to its position in the HM symbol.

In practice, the popular though ill-defined symmetry elements took over from the operations. Thus, b came to be seen as a glide plane, Eb in our present terminology. There is no harm in that re-interpretation except when the operation belongs to an Ee-glide plane. If this holds, for instance, for the above b-glide reflection, then there is an Ee but no Eb-glide plane in the corresponding orientation. In this case, b becomes a very misleading character. Apart from this, the bias (given to b over a or c) is just as disturbing as in the case of the symmetry-element symbols treated in §1.

Therefore, it is proposed to replace such misleading letters a or b by e in all five HM symbols in which they occur:

Space group No.	39	41	64	67	68
Symbol in ITA83:	Abm2	Aba2	Cmca	Cmma	Ccca
New symbol:	Aem2	Aea2	Cmce	Cmme	Ccce.

A further advantage of the proposed new symbols is that e - unlike a or b - is neutral and is therefore not changed upon axis permutation.

4. Printed symbols for symmetry operations

A complete set of print symbols was designed by W. Fischer & E. Koch (ITA83, §11.2) and was extensively applied in the Symmetry Operations sections of the space-group descriptions.

In short, each symbol consists of up to three parts. The first part is a single character (sometimes with an index) which describes the kind of operation. The following part(s) give(s) the components of any relevant shift or translation vector - always in parentheses - and the coordinates of the operation's geometric element, in that order.

The Ad-hoc Committee, after considering this system, wishes to introduce two modifications for glide reflections:

(i) instead of the present first character (which may be a, b, c, n, d or g), always write the letter g;

(ii) always write the glide-vector components (in parentheses) in full, in particular for the simple glide reflections in a-, b- or c-glide planes where they were previously omitted.

Rule (i) suppresses information about the kind of glide plane to which the operation belongs. Very often that information is irrelevant or even confusing. For a/b/c planes the suppression can destroy essential information, but the loss is restored by rule (ii) as shown in the example below.

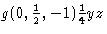By adopting these changes, the uniformity of symbols - also with respect to those for rotations - is greatly improved. For instance, the symbol of the glide reflection in the plane $x = \frac{1}{4}$ , with the unusual glide vector $(0, \frac{1}{2}, -1)$ , namely $g(0, \frac{1}{2}, 1) \frac{1}{4}yz$ , now falls in line with that for a simple b-glide reflection. In ITA83 the latter was denoted by $b \frac{1}{4} y z$ , but this is changed by rule (ii) into $g(0, \frac{1}{2}, 0) \frac{1}{4} y z$ .

The above rules apply equally to glide reflections belonging to the element set of a mirror plane. Thus, if the shift component of such an operation is (0, 1, 2), then its symbol begins with g(0, 1, 2), not with m(0, 1,2).

References

International Tables for Crystallography (1983). Vol. A, edited by TH. HAHN, especially §§ 1.1, 1.3, 1.4, 7 and 11. Dordrecht: Kluwer Academic Publishers.

International Tables for Crystallography (1989). Vol. A, 2nd, revised, ed., edited by TH. HAHN. Dordrecht: Kluwer Academic Publishers.

WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H., FISCHER, W., HAHN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.

WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.

...vectors.: The glide-plane symbols c, n and k for the three diagrams (2), (9) and (14) of Fig. 3 have of course been assigned according to Table 3. One member of the Ad-hoc Committee (Professor Wondratschek) thinks that the symbol n for diagram (9) conflicts with traditional notions about n planes. He proposes the assignment of a special symbol to diagram (9). This proposal has, however, not received adequate support within the Ad-hoc Committee.

These pages are maintained by the Commission Last updated: 15 Oct 2021