Optimization of Patterson map correlation for electron density and its square: relationships for phase extension and refinement
Douglas M. CollinsGeo-Centers, Inc., 10903 Indian Head Highway, Fort Washington, MD 20744, USA
mailing address: 6030 Naval Research Laboratory, Washington, DC 20375-5341, USA
[email protected] John H. Konnert
Laboratory for the Structure of Matter, 6030 Naval Research Laboratory, Washington, DC 20375-5341, USA
[email protected] James M. Stewart
P.O. Box 472, McConnellsburg, PA 17233-0472, USA
[email protected]
Abstract
An objective function is described for optimization of Patterson map correlation for electron density and its square. The function provides excellent discrimination against all zero phases, and is analyzed to find relationships for phase extension and refinement. The objective function and phasing relationships can be calculated rapidly by convolution methods and are practical for application to macromolecular structure determination problems.
1 Introduction
We became interested in this project because the reported power of Debaerdemaeker & Woolfson's [1] phasing function
![]() , (1)
, (1)
XMY hereafter, has not been adequately explained. XMY as a method of phase determination is based on maximizing ![]() by changing phases, one at a time. The phases are carried in
by changing phases, one at a time. The phases are carried in
![]() , and (2)
, and (2)
![]() , (3)
, (3)
where ![]() is a (complex) normalized structure factor associated with the reciprocal-lattice vector h. For noncentrosymmetric structures, the sum in equation (1) excludes Friedel mates and is enantiomorph specific; when XMY is a maximum, the sum using Friedel mates will have the same maximum for the other enantiomorph. This highlights but does not explain the role of
is a (complex) normalized structure factor associated with the reciprocal-lattice vector h. For noncentrosymmetric structures, the sum in equation (1) excludes Friedel mates and is enantiomorph specific; when XMY is a maximum, the sum using Friedel mates will have the same maximum for the other enantiomorph. This highlights but does not explain the role of ![]() , which is of opposite sign for the two enantiomorphs.
, which is of opposite sign for the two enantiomorphs.
While we were not able to add directly any new insight into XMY and its use, we became aware that maximizing a different function, the sum of ![]() , has physical significance that is easy to understand. This function corresponds to the pointwise sum of the product of two Patterson functions, the Patterson for the experimental structure (phase independent) and the Patterson for the squared structure (dependent on the current phase estimates). Thus, maximizing the sum of squares of X and Y corresponds to maximizing the correlation between the two Patterson functions.
, has physical significance that is easy to understand. This function corresponds to the pointwise sum of the product of two Patterson functions, the Patterson for the experimental structure (phase independent) and the Patterson for the squared structure (dependent on the current phase estimates). Thus, maximizing the sum of squares of X and Y corresponds to maximizing the correlation between the two Patterson functions.
Maximizing the correlation between two Patterson functions has a long history in crystallography. One such application is the rotation function of Rossmann and Blow [2]. Another application that has many similarities to what we report here is the work of Ruis [3].
In order to evaluate the potential usefulness of the sum of ![]() as an objective function for phase refinement, we will demonstrate that its value decreases as random errors of increasing size are added to correct phases. Although this property is not sufficient, it is necessary. It is straightforward to test and it has been tested for structures ranging from tens to thousands of atoms. In addition, tests with both a 40-atom structure and a 320-atom structure show our objective function has a local maximum for correct phases, and that maximum is greater than the function value with all phases set to zero. Moreover, for the 40-atom structure maximization of the objective function reduces an average random phase error of 60° to an average error below 10°, at convergence, for
as an objective function for phase refinement, we will demonstrate that its value decreases as random errors of increasing size are added to correct phases. Although this property is not sufficient, it is necessary. It is straightforward to test and it has been tested for structures ranging from tens to thousands of atoms. In addition, tests with both a 40-atom structure and a 320-atom structure show our objective function has a local maximum for correct phases, and that maximum is greater than the function value with all phases set to zero. Moreover, for the 40-atom structure maximization of the objective function reduces an average random phase error of 60° to an average error below 10°, at convergence, for ![]() > 1.3.
> 1.3.
We will discuss the application of this function in cases of macromolecules with limited data. This has in view the not uncommon situation of incomplete phase information to be propagated throughout a set of structure moduli, e.g., complete structure solution from a subset of phases determined by multiple wavelength anomalous diffraction methods.
In the following material we shall develop relationships which make both explicit and implicit use of ![]() , and show that, in general,
, and show that, in general, ![]() cannot be zero for noncentrosymmetric structures. Woolfson [4] gives an overview of the related literature.
cannot be zero for noncentrosymmetric structures. Woolfson [4] gives an overview of the related literature.
2 Cross-correlation
In this section we present reciprocal space formulations of cross-correlation to display explicitly ![]() and
and ![]() as Fourier coefficients. Unless otherwise noted, the density functions used hereafter are not true electron density functions, but the sharpened, rescaled functions obtained by Fourier transformation of E or similar coefficients. In the case of a squared density, the coefficient is written
as Fourier coefficients. Unless otherwise noted, the density functions used hereafter are not true electron density functions, but the sharpened, rescaled functions obtained by Fourier transformation of E or similar coefficients. In the case of a squared density, the coefficient is written ![]() .
.
The convolution theorem leads directly to formulation of the cross-correlation of density and its square through transformation of a product of their coefficients. The cross-correlation is the convolution ![]() and is represented by
and is represented by ![]() .
.
![]() , where (4)
, where (4)
![]() , (5)
, (5)
![]() , (6)
, (6)
and the number of points sampling the unit cell volume V is ![]() , each point given by its position vector r. The convolution theorem also leads directly to formulation of a product of functions as the transform of a convolution of their coefficients, so that
, each point given by its position vector r. The convolution theorem also leads directly to formulation of a product of functions as the transform of a convolution of their coefficients, so that
![]() , and (7)
, and (7)
![]() . (8)
. (8)
Here and elsewhere it is assumed that density functions are real, and consequently a coefficient and its Friedel mate are complex conjugates of each other. With the definitions given in (2) and (3), a little rearrangement of the cross-correlation yields
![]()
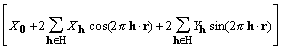 , (9)
, (9)
where H is a half lattice. H is defined as a set of reciprocal lattice vectors excluding h = 0 and any vector that is the negative of a member of the set.
It is clear that the product ![]() will not generally have a phase of 0 or 180, the cross-correlation will not be centrosymmetric for noncentrosymmetric densities, and the values of Y will not all be zero. Moreover, except for structures in which the atoms are all individually centrosymmetric and cleanly resolved in the density function, the maximum of the cross-correlation function will lie near, but not necessarily at, r = 0. This last remark appears to have no practical significance, but it is important that for the correct structure and phases the values of Y are not all zero, and we shall preserve them in the relationships to follow.
will not generally have a phase of 0 or 180, the cross-correlation will not be centrosymmetric for noncentrosymmetric densities, and the values of Y will not all be zero. Moreover, except for structures in which the atoms are all individually centrosymmetric and cleanly resolved in the density function, the maximum of the cross-correlation function will lie near, but not necessarily at, r = 0. This last remark appears to have no practical significance, but it is important that for the correct structure and phases the values of Y are not all zero, and we shall preserve them in the relationships to follow.
At its origin, the cross-correlation of density and its square is the sum of![]() , apart from constant factors. Maximization of that sum by setting to zero its derivative with respect to a phase leads to the standard tangent formula [4].
, apart from constant factors. Maximization of that sum by setting to zero its derivative with respect to a phase leads to the standard tangent formula [4].
Although the origin peak is the major indicator of similarity between density and its square, the remainder of the cross-correlation function is important also. This is illuminated in a simple thought experiment in which the squared density becomes identical to the original density, and the cross-correlation therefore reduces to the Patterson map of the original structure. Because Patterson methods for structure solution largely ignore the origin peak and depend on all the rest of the function, the clear implication is that the off-origin portions of cross-correlation maps are expected to carry important structural information.
3 An objective function related to cross-correlation
An alternate form of the cross-correlation of density and its square is
![]() . (10)
. (10)
For any set of phases, an objective function informed by the entire cross-correlation function is the sum of the squares of the cross-correlation values over all sample points in the unit cell. To find this sum, we use Parseval's theorem,
![]() ,
,
where upper and lower case symbols represent Fourier transform pairs. By Parseval's theorem the sum of the function squared equals the sum of the coefficients squared so that
![]() . (11)
. (11)
It is noted that
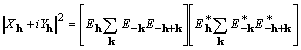 (12)
(12)
![]() , (13)
, (13)
and because ![]() is the coefficient of a Patterson map
is the coefficient of a Patterson map ![]() , and similarly
, and similarly ![]() of
of ![]() , by Parseval's theorem it is also true that
, by Parseval's theorem it is also true that
![]() . (14)
. (14)
The right-hand sides of (11) and (14) are the objective function to be considered, and it is referred to as XSPYS. We prefer the formulation of equation (14) for its computational clarity, and for its evident physical significance, specifically, that ![]() is independent of any phase assignment.
is independent of any phase assignment.
The objective function used in calculations is modified to remove the effect of a structure's self-vectors by removing the origin peak in a Patterson map. The reduced objective function is referred to as XSPYS' given by
![]() , (15)
, (15)
where the origin-removed Patterson map ![]() has coefficients (
has coefficients (![]() ).
).
For any set of structure moduli given as ![]() , we expect XSPYS' to be a maximum for a set of correct phases. This expectation is based on interpretation of the left-hand sides of (11) and (14) and is empirically confirmed for two structures, one a sugar with 40 atoms in the unit cell, and the other a protein with 642 residues and about 5000 atoms in the unit cell. Both structures are in space group P1, and the confirmation is based on evaluation of XSPYS' with perfect structure moduli and varying amounts of error added to the phases.
, we expect XSPYS' to be a maximum for a set of correct phases. This expectation is based on interpretation of the left-hand sides of (11) and (14) and is empirically confirmed for two structures, one a sugar with 40 atoms in the unit cell, and the other a protein with 642 residues and about 5000 atoms in the unit cell. Both structures are in space group P1, and the confirmation is based on evaluation of XSPYS' with perfect structure moduli and varying amounts of error added to the phases.
The simulations were carried out with a simple protocol taking advantage of the convolution theorem and calculating simple products and transforms, arriving finally at evaluation of XSPYS' by computing the left-hand side of (15). A simplification and rescaling were used for the squared density function. After density is squared, it is rescaled to have the same mean value as the original density, ![]() is calculated by inverse Fourier transformation, and if the average value of
is calculated by inverse Fourier transformation, and if the average value of ![]() ,
, ![]() is scaled down to achieve the equality. A simplified choice was made for
is scaled down to achieve the equality. A simplified choice was made for ![]() by setting
by setting ![]() . The protein used in the simulations is D-glycerate dehydrogenase [5], and XSPYS' was computed at 13 levels of random phase error averaging 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, and 120, each set repeated with the structure factor set truncated at resolutions of 2.0, 2.5, 3.0, 4.0, and 5.0 Å (minimum interplanar spacing). The sugar is β-lyxose, a P212121 structure [7] treated as though in space group P1; each molecule has 10 atoms ignoring hydrogen, five carbon and five oxygen atoms, and the unit cell contains four molecules or 40 atoms. Lyxose calculations used the same plan of introducing phase error, but the calculations were made only for the full structure factor set of resolution 0.75 Å.
. The protein used in the simulations is D-glycerate dehydrogenase [5], and XSPYS' was computed at 13 levels of random phase error averaging 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, and 120, each set repeated with the structure factor set truncated at resolutions of 2.0, 2.5, 3.0, 4.0, and 5.0 Å (minimum interplanar spacing). The sugar is β-lyxose, a P212121 structure [7] treated as though in space group P1; each molecule has 10 atoms ignoring hydrogen, five carbon and five oxygen atoms, and the unit cell contains four molecules or 40 atoms. Lyxose calculations used the same plan of introducing phase error, but the calculations were made only for the full structure factor set of resolution 0.75 Å.
It is unremarkable that XSPYS' behaves well in the case of lyxose. But it also behaves well for all the protein calculations, with the plot of XSPYS' against average phase error being a Gaussian above the baseline of completely randomized phases. The Gaussian falls to half-height at 29 average phase error introduced in the 2.0 Å case, and 41 in the 5.0 Å case; its radius of curvature at the origin degrades by an order of magnitude in reducing resolution from 2.0 Å to about 3.4 Å, and two orders of magnitude from 2.0 Å to about 4.8 Å. All the calculations were repeated with a starting point of all phases zero. One remarkable feature of XSPYS' is that in starting from all zero phases it has a value corresponding to completely randomized phases and effectively traces that baseline as increasing random phase shifts are introduced.
4 A derivative and tangent formula from XSPYS'
Solution of the phase refinement problem is sought in a Newton method [8]. Specifically, with ![]() representing XSPYS' evaluated for a phase set, the next iterate of phases would then be
representing XSPYS' evaluated for a phase set, the next iterate of phases would then be
![]() , (16)
, (16)
for which the gradient is required, as is an estimate of the Hessian inverse. Equation (12) may also be written
![]()
![]() , (17)
, (17)
for which a corresponding gradient element is
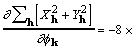
![]() , (18)
, (18)
where the factor 8 accounts for redundant subscript arrangements. Some additional rearrangement that makes use of (7) leads to
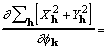
![]() . (19)
. (19)
With a side condition of constant scale for the squaredstructure coefficients, equation (19) is the derivative of XSPYS' with respect to ![]() .
.
At the maximum of XSPYS with respect to any phase, the left-hand side of (19) is zero. Rearrangement of (19) then leads directly to
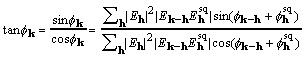 , (20)
, (20)
called here the CKS formula. The CKS formula can be used directly and successfully with the customary practice of restricting the elements that enter the sum. But for data sets with structure factors numbering in the tens of thousands, it is desirable to take advantage of the convolution theorem and the computational efficiency of Fourier transformation.
Assume ![]() determined as described in §3, and form the transform pair
determined as described in §3, and form the transform pair
![]() , (21)
, (21)
![]()
![]() . (22)
. (22)
Transformation of the product of the original density and yields
![]() , (23)
, (23)
and by the convolution theorem,
![]() . (24)
. (24)
Inspection of equations (20), (23), and (24) show that ![]() calculated by the CKS formula is functionally the same as
calculated by the CKS formula is functionally the same as ![]() , the two differing in the details of their calculation. Moreover, by rearrangement of (19),
, the two differing in the details of their calculation. Moreover, by rearrangement of (19),
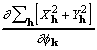
![]()
![]() , (25)
, (25)
and both the derivative and CKS tangent formula phase can be calculated in a sequence of simple multiplications and Fourier transformations.
In §3 we have described some properties of XSPYS' as an objective function to be maximized, calling special attention to its excellent discrimination against all zero phases. For the diagonal approximation of considering phases one at a time, in each simulation calculation described in §3 we made some relative comparisons involving the derivatives of the objective functions XSPYS' and ![]() . We also compared the phases
. We also compared the phases ![]() and
and ![]() , both calculated using the convolution theorem. The objective function derivatives with respect to
, both calculated using the convolution theorem. The objective function derivatives with respect to ![]() are proportional to
are proportional to ![]() and to
and to ![]() .
.
There are 53,362 reflections in the 2.0 Å structure factor set for D-glycerate dehydrogenase and each was counted in the categories good or bad depending on whether the distance of ![]() or
or ![]() from the true phase was better or worse than the distance between the starting and true phases. In similar fashion the reflections were categorized with respect to the signs of the derivatives, that is, whether the indicated shift from starting phase to
from the true phase was better or worse than the distance between the starting and true phases. In similar fashion the reflections were categorized with respect to the signs of the derivatives, that is, whether the indicated shift from starting phase to ![]() or
or ![]() was in the direction of the true phase. In the middle range of introduced error, from about 20 to 60°, the ratios of good to bad derivatives are about 2:1 for both XSPYS' and
was in the direction of the true phase. In the middle range of introduced error, from about 20 to 60°, the ratios of good to bad derivatives are about 2:1 for both XSPYS' and ![]() . The situation is different for
. The situation is different for ![]() and
and ![]() . The ratio of good to bad is about 2:1 for
. The ratio of good to bad is about 2:1 for ![]() , but about 1:1 for
, but about 1:1 for ![]() . This last result leaves open the possibility that the CKS formula calculated with full convolutions is useful for dealing with macromolecules.
. This last result leaves open the possibility that the CKS formula calculated with full convolutions is useful for dealing with macromolecules.
5 A demonstration of phase refinement
The lyxose structure described in §3 was used as a simple test case to demonstrate that maximization of XSPYS' can be used for phase refinement. The tests were successful and show that XSPYS' not only indicates phase error through reduction in its value as error increases, but its maximization through phase adjustment can move the phases in an imperfect set toward their correct values. In the three trials, maximization of XSPYS' was carried out by a quasi-full-matrix truncated-Newton method [8]. In this method, the initial estimate of the Hessian inverse is taken to be the identity matrix, and a corrected estimate is constructed as the calculations proceed.
The three trials were started with average phase error of 0°,20°,and 60°, respectively. The data were taken to be the complete set of ![]() for a total of 2949 phases to be refined. In the case of starting with 60° average phase error, at the maximum of XSPYS' the
for a total of 2949 phases to be refined. In the case of starting with 60° average phase error, at the maximum of XSPYS' the ![]() -weighted
-weighted
| Table 1. After phase refinement, phase error distribution by magnitude of the normalized structure factors |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
average phase error was 21°; a summary of the phase error distribution is given in Table 1. In the case of starting with 20° average phase error, at the maximum of XSPYS' the ![]() -weighted average phase error was 9.7°; a summary of the phase error distribution is given in Table 1. Similar results were obtained with data at 1.2 Å resolution. In the case of starting with perfect phases, attempted maximization of XSPYS' did not lead to any change.
-weighted average phase error was 9.7°; a summary of the phase error distribution is given in Table 1. Similar results were obtained with data at 1.2 Å resolution. In the case of starting with perfect phases, attempted maximization of XSPYS' did not lead to any change.
The truncated-Newton method was used here only to demonstrate feasibility using algorithms applicable to very large structure problems. For problems of modest size such as this example, it is entirely possible that computing resources may be better used by explicit evaluation of the Hessian matrix and application of the classical Newton method [8].
6 Summary and conclusions
Our intent in beginning this work was to understand XMY with a view toward developing for macromolecules some useful phasing relationships that included the evidently important ![]() . The first stages of the work have been successfully completed with identification of XSPYS', an objective function that includes
. The first stages of the work have been successfully completed with identification of XSPYS', an objective function that includes ![]() . XSPYS' powerfully discriminates against all zero phases, and, by the inclusion of
. XSPYS' powerfully discriminates against all zero phases, and, by the inclusion of ![]() , preserves and maximizes the enantiomorphic signal of a noncentrosymmetric structure. The related CKS tangent formula corresponds to a diagonal approximation of phasing through adjustment of phases one at a time. The simulation results show the CKS tangent formula phases can be successfully evaluated through use of convolutions, and give clear indication that
, preserves and maximizes the enantiomorphic signal of a noncentrosymmetric structure. The related CKS tangent formula corresponds to a diagonal approximation of phasing through adjustment of phases one at a time. The simulation results show the CKS tangent formula phases can be successfully evaluated through use of convolutions, and give clear indication that ![]() may be useful in phasing macromolecular structures.
may be useful in phasing macromolecular structures.
The diagonal approximation of adjusting one phase at a time is clearly less powerful than accounting for the phase correlations by adjustment of all the phases together in a full-matrix or quasi-full-matrix solution of maximizing XSPYS'. The first stage of a quasi-full-matrix solution to the phase refinement problem has been successfully completed. Rapid and complete computation of the objective function and all first derivatives by convolutions has been demonstrated, as well as solution of a simple set of test problems. These results will be used in the next stage as a general and efficient software package is constructed for a quasi-full-matrix solution to the phase refinement problem.
We thank Dr. J. Karle for helpful discussions of the work reported here. This research was supported in part by the Office of Naval Research. One of us, JMS, was supported in part by the Office of Naval Research through grant N0001492J1556.
References
[1] T. Debaerdemaeker and M. M. Woolfson, "On the Application of Phase Relationships to Complex Structures. XXVIII. XMY as a Random Approach to the Phase Problem," Acta Cryst. Vol. A45, 349-353, 1989.
[2] M. G. Rossmann and D. M. Blow, "The Detection of Sub-Units within the Crystallographic Asymmetric Unit," Acta Cryst. Vol. 15, pp. 24-31, 1962.
[3] Jordi Ruis, "Derivation of a New Tangent Formula from Patterson-Function Arguments," Acta Cryst. Vol A49, pp. 406-409, 1993.
[4] M. M. Woolfson, "Direct Methods - from Birth to Maturity," Acta Cryst. Vol. A43, pp. 593-612, 1987.
[5] J. D. Goldberg, T. Yoshida and P. Brick, private communication [6], 1994.
[6] F. C. Bernstein, T. F. Koetzle, G. J. B. Williams, E. F. Meyer, Jr., M. D. Brice, J. R. Rodgers, O. Kennard, T. Shimanouchi, and M. Tasumi, "The Protein Data Bank: A Computer-based Archival File for Macromolecular Structures," J. Mol. Biol. Vol. 112, pp. 535-542, 1977.
[7] A. Hordvik, "The Crystal and Molecular Structure of β-Lyxose," Acta Chem. Scand. Vol. 20, pp.1943-1954, 1966.
[8] Stephen G. Nash and Ariela Sofer, "Linear and Nonlinear Programming," pp.302-304 and 391-395. McGraw-Hill: New York, 1996; ISBN 0-07-046065-5.
These pages are maintained by the Commission Last updated: 15 Oct 2021


![[Commission Home Page] [Commission logo]](https://www.iucr.org/__data/assets/image/0008/149381/cc_textlogo.png)