Electron density representation and real-space refinement
(New tricks from an old dog)
E. Blanc, G. Zhou, Z. Chen‡, Q. Xie§, J. Tang, J. Wang and M. S. Chapman§Institute of Molecular Biophysics, § Chemistry Department and ‡ Physics Department, Florida State University, Tallahassee, FL, 32306-3015, USA
chapman@sb.fsu.edu
http://www.sb.fsu.edu/~chapman
Abstract
The expected electron density for an atomic model is calculated directly from the coordinates in a resolution-dependent manner. Several applications are discussed. Firstly, it is possible to refine atomic models in real-space, by optimizing the fit of the model to a map. The methods are conceptually similar to those of Diamond [Acta Crystallogr., 1971. A27: p. 436-452], but much improved through modeling of the resolution limits and inclusion of stereochemical restraints. The methods have been used for complete refinement of virus structures, for local refinement to enhance model-building, and as a pre-refinement method to improve the refinements of proteins by conventional reciprocal-space methods. Secondly, improved local measures of quality can be calculated, comparing the calculated and observed electron densities. Finally, the refinement methods can be applied at about 30 Å resolution to optimally fit known atomic structures into electron microscope reconstructions of large macromolecular complexes.Introduction
Objectives
The objectives are improved methods of structure determination, refinement and analysis, applicable to large macromolecules visualized at medium to low resolution.
The methods discussed increase the data:parameter ratio and have the potential to reduce overfitting and increase the speed with which structures can be determined.
The refinements are based on improved methods for comparing the electron density values of a map with those expected from a model. These comparisons can also lead to improved methods for determining the local quality of a structure, and for assessing the significance of conformational differences.
History
Real-space methods
The fundamentals are not new. In 1971 Diamond [1] published an atomic refinement program that minimized:
ρmap and ρmodel are electron density values -- for the experimental map and calculated from the model; is a position vector for a point in the map, S,k are scaling constants, and P is the set of atomic parameters: x,y,z atomic coordinates and the B-factor. The atomic parameters, P, are adjusted to minimize the residual. A similar function is minimized in RSR of Frodo and ÒOÓ [2].
In these earlier implementations, the electron density was calculated from the model by placing spherical Gaussian functions at each atom center. Spherical Gaussian functions are a good approximation at near-infinitely high resolution.
Diamond and Jones [1, 2] approximated the effects of a resolution limit by smearing the atoms with an additional B-factor. This does not give the expected truncation ripple. The bad effects of this poor approximation can be minimized by disregarding grid points that are not very close to the atom center, as in the RSR implementation. So, some of the data is ignored during refinement. Furthermore, the process becomes a bit more like peak fitting. This works less well at low (~3Å) resolution where there are not discrete peaks for individual atoms.
Both Diamond and Jones [1, 2] incorporated geometrical constraints. Some parts of the model were constrained to good stereochemistry and others were allowed to distort to move the model into electron density. Good stereochemistry was reimposed by alternating real-space refinement with energy minimization [3] or geometric regularization [4]. Often, models oscillate between good fit and good geometry, and convergence is poor.
Restrained reciprocal-space refinement
Reciprocal-space methods soon became more popular because of several advantages:
- Independence from phases: the map used in real-space refinement may incorporate large random errors (e.g., from isomorphous replacement) or systematic errors resulting in bias if a phasing model has been used.
- Simultaneous refinement against geometrical restraints.
For most purposes reciprocal-space refinement is still the most appropriate. We will discuss a few applications for which real-space refinement is better or where it enhances the performance of reciprocal-space methods.
Reciprocal-space methods also have some problems:
- Independence from phases: This is usually considered an advantage, but note also that some of the experimental information is being excluded. At the end of refinement, it is usually best to be phase-independent, but, as discussed later, it is often more important to include all experimental information at the start of refinement.
- Each |F| depends on every atom; therefore,
-
- The refinement of different atoms is interdependent. Conditioning and convergence can be poor.
- It is difficult to access local quality within a structure.
- A Fourier transform must be computed on every cycle. This can be very costly for asymmetric units with many copies of the same subunit.
Pseudo-real-space refinement (authors’ nomenclature)
Some refinements minimize functions of the form:
Like real-space refinement, they use the phases. Stereochemical restraints are usually applied. Due to computation in reciprocal-space, resolution is trivial to incorporate, but the methods are no longer very suitable for small parts of the asymmetric unit., i.e., they are not local methods.
At least one of these implementations is available in most popular refinement packages. Although our own interests are in "real" real-space refinement (below), some of our results are also applicable to these ìpseudo" methods.
Overview of new methods
Our methods combine the best features of Diamond-style and pseudo-real-space refinements. They:
- Include phases
- Include stereochemical restraints
- Account for the resolution of the map
- Are local and therefore quick to calculate for small parts of the structure
Theory
General
Here, the calculation of electron density from a model will be described in a conceptual manner. Mathematical derivations are published elsewhere [7].
- The structure is considered to be a sum of Individual isolated atoms.
- Calculation of the atomic electron density function for each atom uses the definition of a scattering factor, f, that is the Fourier transformation of an isolated atom. The electron density is calculated from the inverse transform: ρ = FT(f). (Anomalous scattering effects are ignored.)
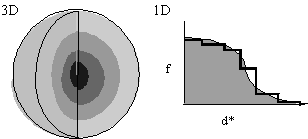
- In the interests of speed, let f(d*) be spherically symmetric (Fig. 1), decreasing with resolution. f(d*) is either calculated from first principles or read from International Tables.
Approximation of f(d*) in one-dimension by steps of uniform scattering (Fig. 1, left) corresponds to concentric spherical shells of uniform scattering in three-dimensions. Now:
This is quick and easy to calculate, because the Fourier transform of a spherical shell has a simple analytical form.
Incorporation of resolution limits
With shells extending out to very high resolution, Fourier transformation of the scattering factor gives a nearly Gaussian function (Fig. 2).
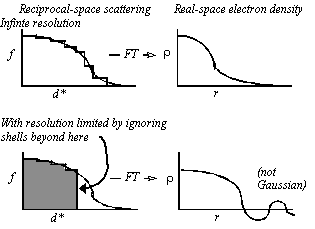 Figure 2 Imposition of resolution limits: Truncation of the scattering beyond a resolution limit leads to ripple which is shown schematically at the bottom right, and leads to a function that is not well approximated by a Gaussian.
Figure 2 Imposition of resolution limits: Truncation of the scattering beyond a resolution limit leads to ripple which is shown schematically at the bottom right, and leads to a function that is not well approximated by a Gaussian.
Resolution limits can be imposed by zeroing the relevant resolution shells. Note that, unlike the Gaussian function, the calculated electron density function has the expected truncation ripple and is not well approximated by a Gaussian. The poor approximation with Gaussian functions is one of the reasons why prior implementations of real-space refinement have not worked well at low resolution.
Implementation
Program “RSRef” compares electron density that was calculated from a model to that of a map, using the residual:
where S and k are scaling constants, and the summation is over all map grid points, that are within rref of the center of any atom. The value of rref is a compromise to be:
1. large enough to include 20-30 grid points/atom,
2. small enough to exclude distant grid points that for which ρmap is less accurate.
Usually, rref ≥ , e.g., rref = 1.6 Å works well with 3Å maps.
The contribution of an atom to the electron density decreases with distance from the center. To speed calculation, it is assumed to be zero beyond a second cut-off distance, rcalc. rcalc needs to be large enough to approximate the overlap of neighboring atoms when viewed at low resolution. It should be ≥ d*max, e.g., ≥ 3.4 Å for 3 Å data.
For refinement, derivatives of the residual are calculated with respect to the atomic parameters. RSRef is written as a module for TNT. The derivatives with respect to electron density are combined (TNT's Shift [8]) with derivatives with respect to the stereochemistry.
Applications
Virus refinement
Summary: Real-space methods are the most appropriate because they are many times faster and use the accurate phases that have been refined by symmetry averaging.
Implementation
Viruses often contain 5 to 120 nearly identical subunits in each asymmetric unit. Only one will be refined. The effects of neighbors will be considered, with regard to:
1. overlapping electron density;
2. non-bonded stereochemical terms.
The neighbors (related by both crystallographic and non-crystallographic symmetry) are regenerated each cycle from the refining protons. Thus, symmetry is imposed as a constraint.
Test case: Canine parvovirus (CPV) empty capsid at 3Å
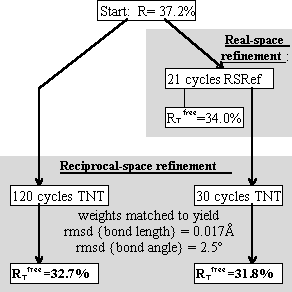
This structure had been previously refined with several batches of reciprocal-space refinement alternated with interactive remodeling [9].
Real-space refinement was compared to 3 of the batches of reciprocal-space refinement, using stereochemical weights chosen to give similar rms deviations to the original refinement.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
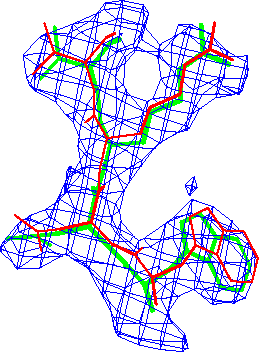
Refinement in real-space appears to be at least as accurate as in reciprocal-space. The difference in these conventional R-factors is modest, but real-space refined model *B* fits the map better than the corresponding reciprocal-space refined model *A* (Fig. 3.).
Actual refinements
CPV DNA-containing virus
Details of the progress of this 2.9 Å refinement are given elsewhere [12], as is a detailed description of an unusual inverted DNA loop (bases pointing out) [13]. Here we will concentrate on refinements of other structures. The only recent result to add is that it was possible to refine a plausible structure for 12 additional N-terminal amino acids that ran through weak, disordered density [20]. As the density runs along a 5-fold axis, the occupancy cannot exceed 20%, and there is biochemical evidence that it is lower. Refinement yielded a model that stayed within the electron density and an occupancy of 13%. It is unlikely that reciprocal-space methods applied at 2.9 Å would have yielded a reasonable model (see below).
Tobacco mosaic virus (TMV)
TMV was refined at 2.4 Å by Bhynavbhatia & Caspar (in preparation), mostly with X-Plor. RSRef was used to refine flexible loops which tended to move out of their weak density with reciprocal-space methods.
At medium resolution, reciprocal-space methods generally lead to poor models of disordered regions. Brünger has recently suggested an explanation [21]: In reciprocal-space refinement, all atoms are interdependent. If an atom is not positioned correctly, other atoms make small adjustments to their positions (perhaps moving away from their correct positions) to improve the overall agreement between experimental and model structure amplitudes. The atoms that are likely to make the largest adjustments are those least restrained by the diffraction data ñ the disordered parts of the model. Our experience with TMV and CPV suggest that real-space refinement is a general method of avoiding this problem, because the refinement is local. Atoms are not adjusted to accommodate for errors in other parts of the model.
Human rhinovirus 50 (HRV50)/WIN 61209
The structure of this virus-drug complex was determined and refined in collaboration with Vince Giranda and colleagues, formerly at Sanofi Withrop Inc. [22]. The revelvant statistics are summarized below:
Unit cell: I222: 310 x 342 x 390 ų
2 x 60 x each of 4 proteins + RNA
Asymmetric unit: 15 x 4 proteins = 15 x 789 amino acids = 93,000 atoms
Diffracts to 1.8Å; refining to 2.0Å;
~ 930,000 independent reflections
Thus, by all measures, this is a large refinement problem.
The starting R factor was 44.4%. Prior to the addition of solvent water molecules, the refinement statistics were:
RTfree = 25.3% to 2.8 Å; 29.9% to 2.0 Å; calculated using all data.
Summary of virus refinement results
Quality
Tests and examples show that real-space refinement compares favorably to reciprocal-space methods. Two advantages probably account for the relatively high quality:
1. Phases are used. After high non-crystallographic redundancy has been exploited, phases are likely more accurate than amplitudes [14].
2. To speed reciprocal-space refinement of viruses, it is common to alternate between subunits of the data. In real space, all the data can be used on every cycle.
Speed
HRV50: Each cycle takes ~ 10 min. cpu on a SGI Indigo workstation. This is comparable to refinement of a protein structure. Empirically, it appears that real space has an N log2N advantage - huge with 15 or 60 N-fold non-crystallographic symmetry. The current version is optimized for minimal memory use (at most ~ 4 Mbytes), through caching of the electron density. With inexpensive memory widely available, it is likely that substantial improvements in speed can be made without the need for caching.
Proteins
Refinement
Expectations for proteins should be much lower:
1. RSRef’s dependence on phases is now a disadvantage (usually).
2. Without high non-crystallographic symmetry there is no speed advantage.
Thus we will be looking at applications in niches that complement the more powerful reciprocal-space methods.
Model-building
Objectives: 1) to increase the speed and precision of interactive modeling
2) to start reciprocal-space refinement closer to the correct structure, to avoid, during optimization, some of the local minima with incorrect conformation.
Implementation
Implementation is conceptually similar to RSR of Frodo/O [15]
a) a small set of residues is defined by various criteria, e.g. residue number, volume.
b) a script to refine the selected fragment(s) is called directly from "O" using a macro.
Differences with RSR have a substantial impact upon results. The major differences are the incorporation of:
a) the map resolution limit.
b) stereochemical restraints.
The availability of an improved local real-space refinement protocol changes the way that models are built in our laboratory.
- Dictionaries are used to set the approximate backbone conformation and side-chain rotamers.
- Real-space refinement is used to optimize the fit to the density.
- As refinement is stereochemically restrained, there is rarely a need to regularize the model or adjust it to relieve close contacts.
- When adjustments are needed, they are made with quick, crude rigid fragment motions followed by real-space refinement.
- There is little need for time-consuming fine adjustments.
Graphics user interface (GUI)
Release 2 of our package includes a GUI through which commonly changed parameters can be changed quickly. The GUI is written in Hypertext Markup Language (HTML) 3.0 [23], as a form, so that it can be displayed with a browser, and is therefore nearly platform independent. The user communicates with a server (that can be a local mirror) which sends back to the client a file containing refinement and control parameters, and refinement, controlled with a Perl script [24], can be started automatically. Alternatively, the refinement can wait for the output of coordinates by an 'O macro. In both cases, the output from refinement is parsed, and essentials are written to the screen. With the ìOî macros, the user has the option of inspecting the refinement results and accepting or rejecting them. Refinement of a few amino acids and their neighbors typically takes about 30 seconds to converge.
How does real-space refinement affect model quality?
Through the use of such techniques, effectively an additional real-space (pre-)refinement step has been inserted between model building and reciprocal-space refinement. Intuitively it seems sensible to optimize the fit to the map before reciprocal-space refinement. In fact, it is suggested in the TNT refinement manual [16], but...
· Does is really do any good?
· Can it do harm if the phases are bad?
Tests
To answer these questions, a test system was needed, which, in contrast to the virus structures, would have phases and electron density as poor as likely to be encountered in protein structure determination. The 3 ? multiple isomorphous replacement (MIR) map of the recently determined HMG Co-A reductase structure [17] was selected. This was a large structure with 2 subunits of 374 amino acids in the asymmetric unit. The average figure of merit was 0.65. The structure had been determined using the 2-fold non-crystallographic symmetry, but for more stringent testing of the real-space refinement, the unaveraged MIR map was used.
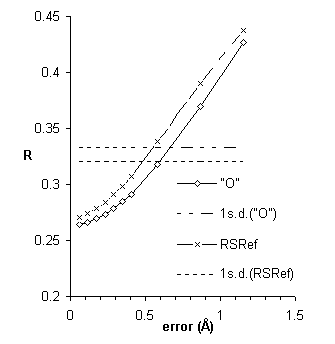
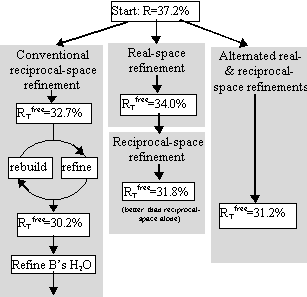
Tests included parallel refinements starting from the unrefined model of the original structure determination [17]. Different refinement protocols were compared, determining how much the model could be improved automatically without intervening model building. The simplest of the tests is shown in Figure 4, a comparison of reciprocal-space refinement with and without real-space pre-refinement.
Real-space pre-refinement leads to improved results. The benefit, which at first sight seems modest, can only be assessed if it is known how good a model can be expected at this early stage of refinement? Following refinement, the model was improved in the original structure determination by several rounds of rebuilding and re-refinement [17]. By resetting the B-factors of the Lawrence et al. final model to 20, and doing 30 additional cycles of positional refinement, we mimicked a model that was not limited by the modeler's abilities, but with fixed B-factors and no solvent, it was an appropriate comparison for early refinement steps. The was 30.2%.
Combined refinement
The benefit of real-space pre-refinement might be limited by the poor quality of the MIR map. Following real-space refinement, improved phases can be calculated from the model. Use of a map calculated with
(2Fo - Fc, αc) allows real-space refinement to progress further. With cycles of map calculation and real-space refinement:
1. the conventional R-factor continues to decrease
2. decreases for 2 cycles then increases – suggesting bad effects of phase bias.
Phase bias can be reduced by inserting reciprocal-space refinement, allowing the atoms to move independently of the phases. Each round of refinement now consists of:
1. real-space refinement
2. reciprocal-space refinement
3. 2Fo - Fc map calculation, then back to #1
Improvement stopped after 2 rounds (with HMG Co-A reductase), monitoring convergence with .
The result was a model with = 31.2%, just 1% above that obtainable after extensive rebuilding and refinement (Fig. 5).
Why does real-space refinement help?
A good indication comes from comparing free and conventional R-factors:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The difference between and Rconv is less with real-space pre-refinement (and
is lower), suggesting that there is less overfitting [18] and better convergence with pre-refinement. Further details of alternated real and reciprocal-space refinements will be published elsewhere [25].
Which real-space method?
The results above would apply equally to the pseudo-real-space methods available in several programs in which is minimized [6].
With pre-refinement, it is convenient to use RSRef, called from “O”, so that the effects can be monitored immediately. When blindly alternating real- and reciprocal-space refinements, either RSRef or a suitable pseudo-real-space method would be appropriate.
Quality indices
Most crystallographic quality indices are global – a measure of the average error of a whole structure. Jones et al. [15] suggested the use of real-space R-factors (or correlation coefficients) calculated by comparing calculated and map electron densities near residues. These indices are suitable to detect gross error, such as sequence, locally mis-aligned with the structure. Our tests have used a similar index:
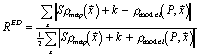
With improved representation of ρmodel , it might be possible to compute a more sensitive indicator of error.
Tests
- All atoms of the CPV structure were moved by a uniform shift vector of randomly chosen direction.
- RED was calculated for each residue.
- RED was averaged between all ~550 amino acids, and the standard deviation of the mean was calculated.
- These calculations were repeated for shifts of different magnitudes.
There is a lot of inherent variability in the strength of electron density, so there is a large component of the variation in the index that is independent of model quality. We are interested in how small a shift is required for the index to rise above this variation.
A suitable criterion to judge quality indices is therefore the smallest shift for which the change in mean index (for all residues) is greater that its standard deviation.
Δμ(index) > σ(index)
Figure 6 plots real-space R-factors vs. introduced error.
The sensitivity of real-space R-factors is improved when calculated using the improved electron density functions of RSRef. However, they remain a quality index of low sensitivity.
Further improvements were inspired by Dale Tronrud’s screening for poor geometry. Poorly fit atoms are likely to have large derivatives, . Well-fit atoms will have small derivatives, independent of the strength of the electron density. As shown in Fig. 7, the magnitude of the gradient, Δρ, is about twice as sensitive as real-space R-factors. Additional details will be published elsewhere [26].
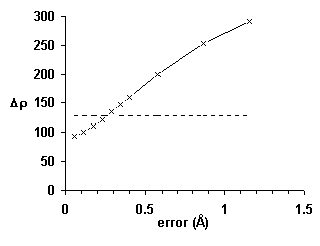 Figure 7 An improved local quality index based on the magnitude of the gradient, Δρ: The average index rises by more than one standard deviation (horizontal line) in less than 0.3 Å.
Figure 7 An improved local quality index based on the magnitude of the gradient, Δρ: The average index rises by more than one standard deviation (horizontal line) in less than 0.3 Å.
Refinement of EM images
Recently, 3-D electron microscope reconstructions have been performed for complexes of molecules whose structures are known at high resolution. Examples include viruses complexed with antibodies and receptors, complexes of muscle components, etc..
Real-space refinement offers the opportunity to optimize the modeling of these reconstructions. RSRef has been adapted for this purpose in several ways:
1. X-ray scattering factors have been replaced by electronic scattering factors.
2. Reduction of the contrast due to solvent scattering has been calculated using modified protein scattering factors from which solvent scattering has been subtracted.
3. Scattering has been attenuated to account for EM incoherence.
RSRef is capable of moving a rigid protein model into EM electron density. This was demonstrated with the 27 Å Cryo-EM 3-D reconstruction of human rhinovirus complexed with antibody fragment Fab 17 [19]. After the Fab had been moved 17Å in a random direction, real-space refinement reduced the RED from 102% to 38% in bringing the Fab back into the electron density.
Improved methods are being developed that will adjust some of the EM experimental parameters to optimize the fit.
Acknowledgements
We thank Cynthia Stauffacher and Martin Lawrence for access to coordinates and data of HMG Co-A reductase prior to publication. We thank Tom Smith, Tim Baker, R. Holland Cheng, and Norman Olson for giving us the cryo-EM data with which the EM refinement methods are being tested. We would like to acknowledge our collaborators on the HRV50 refinement: Vince Giranda, R. S. Alexander, M. McMillan and D. C. Pevear. We are indebted to Mike Sloderbeck for computational advice.
This work has been generously supported by the Lucille P. Markey Charitable Trust and a grant from the National Science Foundation (MSC; BIR9418741).
Distribution
Programs are distributed under license from http://www.sb.fsu.edu/~rsref.
References
1. Diamond, R., A Real-Space Refinement Procedure for Proteins. Acta Crystallogr., 1971. A27: p. 436-452.
2. Jones, T.A. & L. Liljas, Crystallographic Refinement of Macromolecules having Non-crystallographic Symmetry. Acta Crystallogr., 1984. A 40: p. 50-7.
3. Levitt, M., Energy Refinement of Hen Egg-White Lysozyme. J. Mol. Biol., 1974. 82: p. 393-420.
4. Hermans Jr., J. & J.E. McQueen, Computer Manipulation of (Macro)molecules with the Method of Local Change. Acta Crystallogr., 1974. A30: p. 730-9.
5. Rees, D.C. & M. Lewis, Incorporation of Experimental Phases in a Restrained Refinement. Acta Crystallogr., 1983. A39: p. 94-97.
6. Arnold, E. & M.G. Rossmann, The Use of Molecular-Replacement Phases for the Refinement of the Human Rhinovirus 14 Structure. Acta Crystallogr., 1988. A44: p. 270-282.
7. Chapman, M.S., Restrained Real-Space Macromolecular Atomic Refinement using a New Resolution-Dependent Electron Density Function. Acta Crystallogr., 1995. A51: p. 69-80.
8. Tronrud, D.E., L.F. Ten Eyck & B.W. Matthews, An Efficient General-Purpose Least-Squares Refinement Program for Macromolecular Structures. Acta Crystallogr., 1987. A43: p. 489-501.
9. Wu, H., W. Keller & M.G. Rossmann, Determination and Refinement of the Canine Parvovirus Empty-Capsid Structure . Acta Cryst. , 1993 . D49 : p. 572-9 .
10. Hendrickson, W.W., Stereochemically Restrained Refinement of Macromolecular Structures. Meth. Enzym., 1985. 115: p. 252-270.
11. Brünger, A.T., J. Kuriyan & M. Karplus, Crystallographic R factor Refinement by Molecular Dynamics. Science, 1987. 235: p. 458-60.
12. Chapman, M.S. & M.G. Rossmann, Structural Refinement of the DNA-containing Capsid of Canine Parvovirus using RSRef, a Resolution-Dependent Stereochemically Restrained Real-Space Refinement Method. Acta Crystallogr., 1996. D52: p. 129-42.
13. Chapman, M.S. & M.G. Rossmann, Single-stranded DNA-protein interactions in Canine Parvovirus. Structure, 1995. 3: p. 151-62.
14. Arnold, E. & M.G. Rossmann, Effect of errors, redundancy, and solvent content in the molecular replacement procedure for the structure determination of biological macromolecules . Proc. Natl. Acad. Sci. USA , 1986 . 83 : p. 5489-93 .
15. Jones, T.A., J.-Y. Zou, S.W. Cowan & M. Kjeldgaard, Improved Methods for Building Protein Models in Electron Density Maps and the Location of Errors in these Models. Acta Crystallogr., 1991. A47: p. 110-9.
16. Tronrud, D.E. & L.F. Ten Eyck, TNT Refinement Package, Release 5-A . 1992 .
17. Lawrence, C.M., V.M. Rodwell & C.V. Stauffacher, The crystal structure of Pseudomonoas mevalonii HMG-CoA reductase at 3.0 Å resolution. Science, 1995. 268: p. 1758-62.
18. Brünger, A.T., Free R value: a novel statistical quantity for assessing the accuracy of crystal structures . Nature , 1992 . 355 : p. 472-5 .
19. Smith, T.J., N. Olson, R.H. Cheng, H. Liu, E. Chase, W.-M. Lee, A. Moser, R. Rueckert & T.S. Baker, Structure of human rhinovirus complexed with Fab fragments from a neutralizing antibody. J. Virol., 1993. 67: p. 1148-58.
20. Xie, Q. and M.S. Chapman, Canine parvovirus capsid structure, analyzed at 2.9 Å resolution. Journal of molecular biology, 1996. in press.
21. Brünger, A.T. and L.M. Rice, Crystallographic Refinement by Simulated Annealing: Methods and Applications. Methods in Enzymology, 1997. in press.
22. Blanc, E., V. Giranda, R.S. Alexander, M. McMillan, D.C. Pevear, Q. Xie, G. Parthasarathy, and M.S. Chapman, The 2 Å Refined Structure of Human Rhino Virus 50 Complexed with an Antiviral Agent. 1996. in preparation.
23. Graham, I.S., HTML Sourcebook. 2nd ed. 1996, New York: Wiley.
24. Wall, L. and R.L. Schwartz, Programming perl. 1991, Sebastapol, CA: O'Reilly & Associates, Inc.
25. Chapman, M.S. and E. Blanc, Potential use of Real-space Refinement in Protein Structure Determination. Acta Crystallographica, 1996. A: p. accepted for publication.
26. Zhou, G., J. Wang, E. Blanc, and M.S. Chapman, The Use of Real-Space R-factors for the Quantification of Errors in Macromolecular Structures. Acta Crystallographica, 1996. in preparation.
These pages are maintained by the Commission Last updated: 15 Oct 2021


![[Commission Home Page] [Commission logo]](https://www.iucr.org/__data/assets/image/0008/149381/cc_textlogo.png)