Auxetics: Don’t Pull Me, I’ll Get Fatter!

The use of materials is one of the main pillars that has led to humankind’s success. The evolution of the materials we use to manufacture tools, products and structures has allowed for the innovation of more advanced creations, and hence, further advancements of humankind itself. In more recent years, as knowledge of materials having so-called “regular” properties has increased, scientists and engineers gradually began to focus their attention on materials with properties termed “irregular” or anomalous. Anomalous properties are of great interest, leading to a number of possible and previously unattainable modern applications.

Anomalous properties can be divided into (i) anomalous electronic properties, relating to the properties associated with electrons and their interactions; (ii) anomalous structural properties, which refer to properties arising from the arrangement of atoms, grains and other building blocks of a material; and (iii) anomalous mechanical properties, which refer to the response of a material when applying mechanical loads. While both (i) and (ii) are significant subjects of interest in their own right, here we shall focus on an important anomalous mechanical property, namely auxeticity. It should be noted, however, that even though anomalous properties can be divided into categories, we should not assume that there is no “bridging” of one type of property to another. In fact, auxeticity is highly reliant on the structure/geometry of the material, even though it is considered to be a mechanical property.

Auxeticity, a term coined by K. E. Evans and coworkers in 1991 (Evans et al., 1991), can be defined as the material property of having a negative Poisson’s ratio. A visual example of auxeticity is given in Figure 1, which shows how auxetic materials become “fatter” when uniaxially stretched and “thinner” when uniaxially compressed.

Figure 1. (Left) a material behaving in an auxetic manner when uniaxially stretched/compressed, and (right) a material behaving in a conventional manner when uniaxially stretched/compressed.

In order for a material to be auxetic, it must have particular geometric features as well as an amenable deformation mechanism that permits the ‘geometry’ to deform in a fashion that allows for auxetic behaviour to be exhibited. The combination of the two required features creates what can be termed as ‘auxetic mechanisms’, a grouping made in order to simplify the matter, with applicability of these mechanisms in various real situations ranging from natural and synthetic materials, such as crystals or giant nanonetworks, to giant architectural constructs.

There are two main categories of auxetic mechanisms: stretching, whereby structural elements lengthen or slide past each other, such as triangular structures made of ligaments analogous to shock absorbers (Rothenburg et al., 1991) and two-dimensional models of hexagonal molecules on a hexagonal lattice interacting via a nearest-neighbour n-inverse-power site (Wojciechowski, 1987); and rotation, whereby internal units rotate relative to each other such as in the rotating squares mechanism (Grima & Evans, 2000), re-entrant honeycomb mechanism (Kolpakov, 1985) and nodule-fibril mechanism observed in certain polymeric materials (Evans & Alderson, 2000).

Stretching mechanisms, as noted above, are all mechanisms leading to auxeticity that can be attributed to the lengthening of structural elements or sliding of elements past each other. An auxetic mechanism of this type is Rothenburg et al.’s (1991) triangular structures made of ligaments that are analogous to shock absorbers (see Figure 2, left). Here, when applying a uniaxial stress to the structure made of ligaments in any direction, the deformation that occurs causes a reduction in the length of all three units as a result of the shock-absorber-like units present. Another mechanism for auxeticity based on a stretching mechanism is Wojciechowski’s (1987) two-dimensional models of hexagonal molecules on a hexagonal array interacting via a nearest-neighbour n-inverse-power site–site potential (see Figure 2, right): a system that becomes auxetic at high densities because of the repulsion between atoms within the hexagonal system.

Figure 2. Stretching mechanisms leading to auxeticity, specifically Rothenburg et al.’s (1991) hexagonal auxetic structure made of ligaments that are analogous to shock absorbers (left); and Wojciechowski’s (1987) two-dimensional models of hexagonal molecules on a hexagonal array interacting via a nearest-neighbour n-inverse-power site–site potential (right).

More commonly, auxeticity in materials can be attributed to a rotating mechanism that, as noted above, involves the rotation of units relative to each other. Before proceeding any further it should be noted that rotations can also be described in terms of micro-domain changes, rather than simply rotations of a rigid unit around a point, such as in defective graphene. In three dimensions, rotating mechanisms for auxeticity include rotating polyhedra mechanisms. These systems involve rotations of rigid/semi-rigid polyhedra in a manner that results in the elongation in one direction or more when “pulling” the structure, and a reduction in one dimension or more when “pressing” the structure (in particular directions). Such 3D mechanisms have been applied at both the macroscale [e.g. in the structure suggested by Attard & Grima (2012), shown in Figure 3 (left)] and the nanoscale, including crystal structures such as α-cristobalite shown in Figure 3 (right) (Alderson & Evans, 2001).

Figure 3. (Left) connected cuboid structure suggested by Attard & Grima (2012). (Right) rotating tetrahedral model by Alderson & Evans (2001).

Unfortunately, 3D auxetic models can sometimes be rather complex to conceptualise and, as a result, a number of simpler yet equally effective 2D models have also been proposed to explain the auxeticity in materials. In this category, we find mechanisms that are generally referred to as rigid/semi-rigid rotating polygon mechanisms. Because of the high incidence of manifestation in crystal structures when viewed in particular planes, this discussion will be focused on the rotating square/rectangle mechanisms which exhibit a Poisson’s ratios of –1 for loading in any direction (see Figure 4, top). These mechanisms and others such as the rotating triangles mechanism, which have their own applicability, may be regarded as “perfect” auxetic systems, demonstrating auxeticity when stress is applied in any direction. Such perfection is difficult to achieve in real systems such as crystals or foams, and it has been shown that when the polygons in the structure are no longer rigid but semi-rigid, the Poisson’s’ ratio increases from its ideal value of –1, making the structure less auxetic and anisotropic. Such semi-rigid rotating polygon models have been used successfully to explain the auxeticity in various systems including crystals such as α-cristobalite, which can be considered to have a semi-rigid rotating rectangle mechanism in particular crystal faces, as discussed by Grima et al. (2006); Thomsonite (see Figure 4, bottom); natrolite; and a number of others.

Figure 4. (Top) the rotating squares mechanism. (Bottom) the rotating squares mechanism observable in Thomsonite.

Another important 2D mechanism that may feature in materials when viewed in two-dimensional space is the “wine rack” mechanism, where rigid ligaments (which can be considered as the one-dimensional equivalent of polygons) rotate relative to each other in a manner resulting in the wine-rack ‘opening’. The opening of this structure occurs when applying uniaxial stress in certain off-axis directions. If the stress were to be applied on-axis this effect would not be observed, as the structure would deform in a manner to maximise elongation in the direction of loading, and the structure begins to close (Caruana-Gauci et al., 2018). This highlights the anisotropy possible for such a material property. Similar to the wine-rack mechanism for auxeticity described above is the 2D re-entrant honeycomb mechanism. This is also composed of rigid ligaments considered to be the one-dimensional equivalents of polygons rotating relative to each other. Upon the application of uniaxial stress in particular directions, the re-entrant structure begins to expand as shown in Figure 5, with a negative Poisson’s ratio being observed until the structure takes the shape of “rectangles” or “squares”. At the point of achieving this “squareness”, the Poisson’s ratio becomes positive upon further application of stress. This structure is also anisotropic.

Figure 5. Re-entrant mechanism for auxeticity in action. Note how it reaches the described structure composed of “squares”.

Applications of materials with anomalous properties are vast and always growing, including those of materials that exhibit auxeticity. This can be attributed to the fact that certain applications that could not be achieved previously using materials with “regular” properties are now possible because of these “irregular” properties. This statement is true on the macroscale, i.e. materials above the microscale (>0.1 mm), which can usually be viewed by the naked eye; the microscale (0.001–0.1 mm); and the nanoscale (<0.001 mm), as auxetic materials have been considered and applied in applications down to the smallest of sizes.

On the macroscale, applications of auxetic materials and structures include sportswear applications, clothing, furniture, yarns, protection and home improvement. A recent push has also been made towards auxetic architecture, where these materials – owing to the versatility of these structures, their aesthetics and a number of other reasons – are being applied to structures such as the Munich 1972 Olympic Park roof shown in Figure 6 (right), which can be likened to the opened re-entrant structure shown in Figure 6 (left). In the future, such domes could possibly be constructed by the application of auxetic structures in order to reduce time, equipment and materials required to erect these impressive buildings.

Figure 6. (Left) the opened re-entrant structure described above alongside (right) the Munich 1972 Olympic Park roof.

Auxetics in sportswear is currently an interesting field because of the anomalous ability of these structures to “dome”, and therefore take the shape of the subject (e.g. the sole of a foot) better than conventional materials. This can be seen in certain Nike shoes within the Nike Free collection, which use an auxetic sole [see Figure 7(a)], incorporating auxetic geometry consisting of a hexagonal array of triangles [see Figure 7(b)] in order to enhance the running experience; and in those in the Under Armour ClutchFit^TM collection, which have an auxetic upper (see Figure 8) for a "glove-like fit and feel that’s truly customized to every foot", which incorporates a number of different mechanisms throughout their range, including the re-entrant mechanism (see Figure 8, top) and the "arrowhead" mechanism (see Figure 8, bottom).

Figure 7. (a) Nike Inc.’s Free sole alongside (b) the auxetic array of incorporated triangles.

Figure 8. (Top) the idealised representation of the re-entrant mechanism alongside Under Armour Inc.’s ClutchFit, incorporating the re-entrant mechanism on the upper. (Bottom) the idealised representation of the arrowhead mechanism alongside Under Armour, Inc.’s ClutchFit, incorporating the arrowhead mechanism on the upper.

Auxetics have also been suggested and sometimes applied to clothing for both aesthetic and practical reasons. Apart from the obvious aesthetic reasons, they have a couple of advantages over classical textiles. For example, the auxetic clothes designed and manufactured by Petit Pli Ltd have the ability to adjust to the body’s natural contortions better and “grow” with the individual. These may be particularly appealing to pregnant women and growing children, as seen in Figure 9.

Figure 9. Auxetic clothing for children, which “grows” alongside their growth, designed and manufactured by Petit Pli Ltd.

Auxetic furniture has also attracted attention due to its functionality and design. A good way to describe this furniture would be to call it “furniture that you never get bored of” as you can change it as you want or need to. Imagine a table that can be made bigger by simply pulling it or shelves that can be adjusted depending on what you are trying to display (see Figure 10). Using auxetic foams, i.e. foams that have been transformed by pressure and heat treatment [the negative Poisson’s ratio may be explained by the incorporation of the rotating rigid units and/or the re-entrant mechanisms present at the microscale (see Figure 11)] in chairs may increase comfort by placing different foams in different positions, enhancing back support and improving posture, much needed in the digital age. The possibilities in this area are endless.

Figure 10. Shelves incorporating the rotating squares auxetic mechanism by Lee Sehoon.

Figure 11. (Left) the rotating rigid-units explanation (Grima et al., 2005) and (right) the re-entrant explanation (Lakes, 1987) for auxeticity in converted foams.

Another interesting application of auxetics is that of auxetic yarns, particularly those that also exhibit other enhanced properties such as high strength, lightness, high thermal resistivity and durability. Such high-tech yarns tend to have advanced applications such as protective gear for more extreme situations and military applications, such as ballistic protection. On the topic of ballistic protection, auxetics have found their way into a number of protective applications, which include, but are not exclusive to, military applications. Protection can be extended further from yarns, and research is being carried out on auxetic protective barriers, some of which have already been applied for ballistic protection as an alternative to yarns in order to reduce the shock wave of the blast due to vibration damping properties. Apart from the aforementioned ballistic protection, auxetic foams have also been suggested as a means to improve helmets for sports and motoring applications, and work is being carried out in order to determine the best distribution and foam to use. Similar propositions have been made for knee pads, shoulder pads and other protective equipment, and also on the incorporation of an auxetic hard shell on the outside of the protective foam in order to have a better fitting protective pad. A collage of protective applications of auxetics can be seen in Figure 12.

Figure 12. A collage of protective applications of auxetics, featuring (top left) ballistic protection applied to vehicles, (top right) blast protective fabric, (bottom left) blast protective glass curtain concepts and (bottom right) helmets incorporating auxetic foams.

Auxetic home-improvement applications have great potential as they simplify and improve such components. Examples include the auxetic nail, the auxetic screw and auxetic rivets, which become thinner when applying the component, making application easier, and become fatter when applying stress on the fully applied component, providing a better grip on the surface compared with the conventional counterparts. Similar applications of auxetics include seals and gaskets, which are expected to provide a better seal compared with non-auxetic components.

Going down further in size, in the boundary between macro- and microscale one can find auxetic stent applications. These small devices are designed to open up and keep open arteries that are blocked or have collapsed (see Figure 13). The stent itself has two important requirements: to be small upon entry to the circulatory system and to get longer and fatter when reaching its destination by means of a balloon-like device inflating it. These requirements fit perfectly into the applicability range of auxetic materials and structures, and therefore, auxetic stents are truly an ideal solution for this medical requirement.

Figure 13. (Left) stents prior to application (iStock.com/RickLeePhoto), and (right) a section of an auxetic stent (Amin et al., 2015).

Another possible medical application of auxetics is that of pharmaceutical-releasing dressings, a concept that was first proposed by A. Alderson. The idea here is that, for example, the pharmaceutical agent would be trapped within the auxetic pores (e.g. in between the rigid units in a rotating polygons model shown in Figure 14), and when the body part being treated begins to swell, as a result of the auxetic behaviour, the pharmaceutical agent will be released and the swelling/pain would be targeted at just the right time.

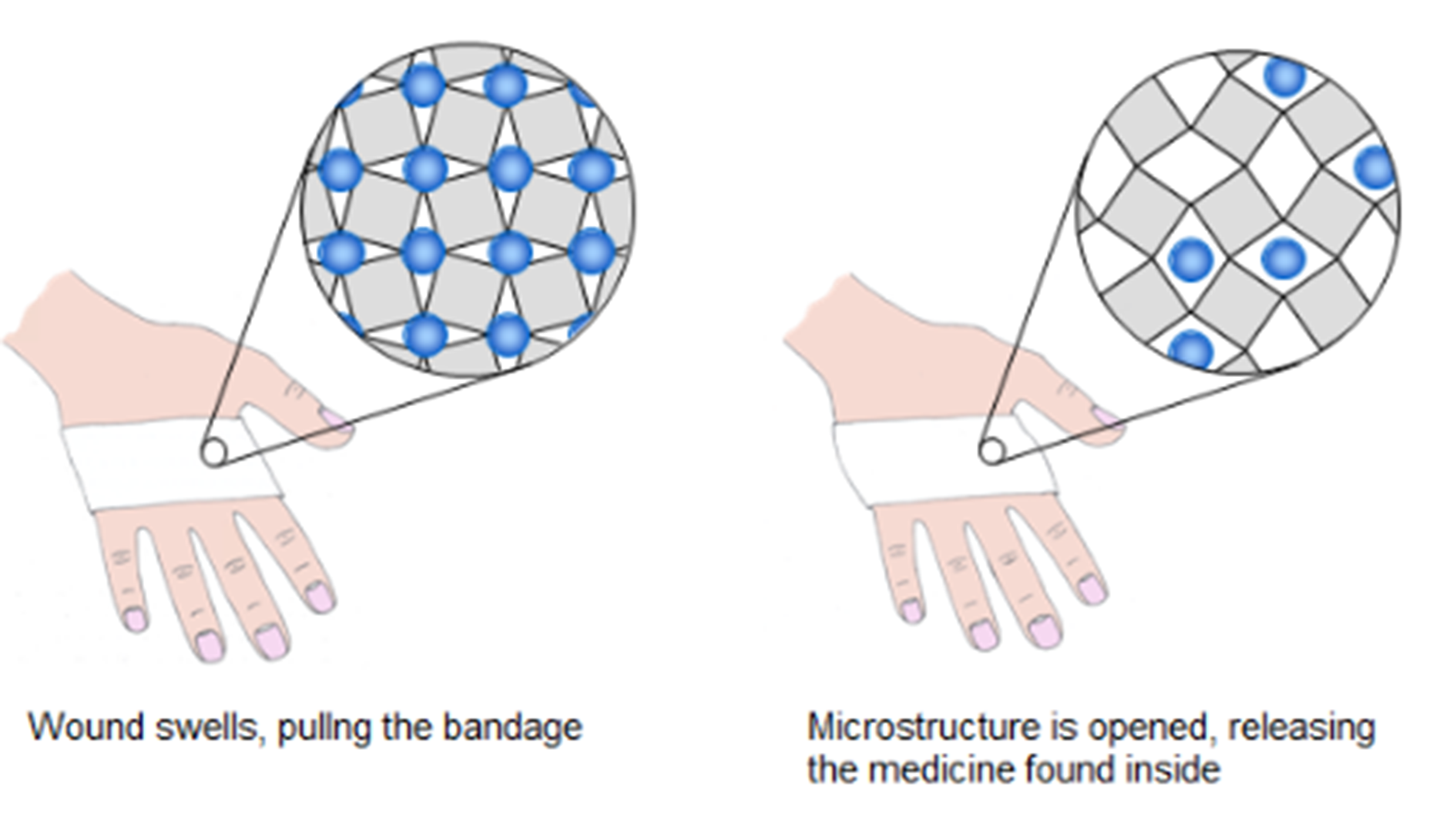Figure 14. Auxetic smart dressings, which release the pharmaceutical agent when required.

Within the lowest scale to be discussed, the nanoscale, a possible application has been suggested for auxetic materials, namely nanofilters. Nanofiltration is filtration at the atomic/molecular level by means of filtration structures built of atomic networks. This is a suggested application of auxetic porous networks of the nanoscale, such as reflexyne, shown in Figure 15, having the ability to have their pore size changed in an auxetic fashion, i.e. the pores are size-tuneable by the application of stress.

Figure 15. Auxetic reflexynes, which can be used as nanofilters (Alderson et al., 2005).

Being a relatively new subject, it is certain that more applications will come about for this highly interesting mechanical property, and as the possible applications increase, so will the demand for materials that exhibit this remarkable property. This is expected to lead to further developments of novel mechanisms that generate auxetic behaviour, which in turn could once again result in other possible applications unknown to us as of yet. It is this continuous "chicken and egg" type research cycle that keeps auxetics driving in the fast lane … along with plain-and-simple curiosity.

I would like to thank Professor Mike Glazer for the opportunity to write in this Newsletter and for all his help in doing so.

References

Alderson, A., Davies, P. J., Williams, M. R., Evans, K. E., Alderson, K. L. & Grima, J. N. (2005). Mol. Simul. 31, 897–905.

Alderson, A. & Evans, K. E. (2001). Phys. Chem. Miner. 28, 711–718.

Amin, F., Ali, M. N., Ansari, U., Mir, M., Minhas, M. A. & Shahid, W. (2015). J. Appl. Biomater. Func. 13, 127–135.

Attard, D. & Grima, J. N. (2012). Physica Status Solidi B, 249, 1330–1338.

Caruana-Gauci, R., Degabriele, E. P., Attard, D. & Grima, J. N. (2018). J. Mater. Sci. 53, 5079–5091.

Evans, K. E. & Alderson, A. (2000). Adv. Mater. 12, 617–628.

Evans, K. E., Nkansah, M. A., Hutcherson, I. J. & Rogers, S. C. (1991). Nature, 353, 124.

Grima, J. N., Alderson, A. & Evans, K. E. (2005). Physica Status Solidi B, 242, 561–575.

Grima, J. N. & Evans, K. E. (2000). J. Mater. Sci. 19, 1563–1565.

Grima, J. N., Gatt, R., Alderson, A. & Evans, K. E. (2006). Mater. Sci. Eng. A, 423, 219–224.

Kolpakov, A. G. (1985). J. Appl. Math. Mech. 49, 739–745.

Lakes, R. (1987). Science, 235, 1038–1041.

Rothenburg, L., Berlin, A. I. & Bathurst, R. J. (1991). Nature, 354, 470–472.

Wojciechowski, K. W. (1987). Mol. Phys. 61, 1247–1258.